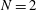JFM Rapids
Universal scaling law for drag-to-thrust wake transition in flapping foils
-
- Published online by Cambridge University Press:
- 07 June 2019, R1
-
- Article
- Export citation
Focus on Fluids
Taming turbulent fronts by bending pipes
-
- Published online by Cambridge University Press:
- 04 June 2019, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
Dynamics in closed and open capillaries
-
- Published online by Cambridge University Press:
- 07 June 2019, pp. 5-38
-
- Article
- Export citation
Propagation of tides along a river with a sloping bed
-
- Published online by Cambridge University Press:
- 07 June 2019, pp. 39-73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear behaviour of the Mack mode in a hypersonic boundary layer
-
- Published online by Cambridge University Press:
- 07 June 2019, pp. 74-99
-
- Article
- Export citation
Dewetting of liquid film via vapour-mediated Marangoni effect
-
- Published online by Cambridge University Press:
- 07 June 2019, pp. 100-114
-
- Article
- Export citation
Lock-in phenomenon of vortex shedding in oscillatory flows: an analytical investigation pertaining to combustors
-
- Published online by Cambridge University Press:
- 07 June 2019, pp. 115-146
-
- Article
- Export citation
Mathematical modelling of a viscida network
-
- Published online by Cambridge University Press:
- 07 June 2019, pp. 147-176
-
- Article
- Export citation
Experiments on flows in channels with spatially distributed heating
-
- Published online by Cambridge University Press:
- 07 June 2019, pp. 177-197
-
- Article
- Export citation
On the detection of internal interfacial layers in turbulent flows
-
- Published online by Cambridge University Press:
- 07 June 2019, pp. 198-217
-
- Article
- Export citation
Modelling fluid deformable surfaces with an emphasis on biological interfaces
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 218-271
-
- Article
- Export citation
Effects of slowly varying meniscus curvature on internal flows in the Cassie state
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 272-307
-
- Article
- Export citation
Healing of thermocapillary film rupture by viscous heating
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 308-326
-
- Article
- Export citation
Mesoscale modelling of near-contact interactions for complex flowing interfaces
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 327-347
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Three-dimensional effects on the transfer function of a rectangular-section body in turbulent flow
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 348-366
-
- Article
- Export citation
Velocity and spatial distribution of inertial particles in a turbulent channel flow
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 367-406
-
- Article
- Export citation
Effects of surfactant on propagation and rupture of a liquid plug in a tube
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 407-437
-
- Article
- Export citation
Superconvergence of a fully conservative finite difference method on non-uniform staggered grids for simulating wormhole propagation with the Darcy–Brinkman–Forchheimer framework
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 438-471
-
- Article
- Export citation
Recovery of wall-shear stress to equilibrium flow conditions after a rough-to-smooth step change in turbulent boundary layers
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 472-491
-
- Article
- Export citation
Lagrangian investigations of velocity gradients in compressible turbulence: lifetime of flow-field topologies
-
- Published online by Cambridge University Press:
- 10 June 2019, pp. 492-514
-
- Article
- Export citation