Published online by Cambridge University Press: 07 June 2019
An analytical investigation is performed to understand the lock-in phenomenon, observed in vortex shedding combustors. Several aeroengine afterburners and ramjets use a bluff body to stabilize the flame. The bluff body sheds vortices. During the occurrence of high-amplitude combustion instability, the frequency of vortex shedding locks in to the frequency of the chamber acoustic field. This phenomenon is termed vortex-acoustic lock-in. In general, there is a two-way coupling between the vortex shedding process and the acoustic field, making analytical investigation difficult. Since the frequency of the latter remains largely unaltered, performing an investigation to study the response of vortex shedding to external excitation not only allows one to gain insights, but also make the problem analytically tractable. We begin with a lower-order model available in the literature to describe the vortex shedding process in non-reacting flows, arising from sharp corners in the presence of upstream velocity excitation. The continuous time domain model is transformed to a discrete map, which connects the time instances of two successive vortex shedding events. The frequency and amplitude of excitation are varied to study the instantaneous vortex shedding time period, as the response of the system. In the absence of forcing, the iterates of the map form a period-1 solution with the frequency equalling the natural vortex shedding frequency. On increasing the amplitude of excitation, quasi-periodic behaviour of the iterates is observed, followed by a period-1 lock-in solution, where vortex shedding occurs at the excitation frequency. On further increasing the amplitude, de-lock-in occurs. From the map, an analytical solution is extracted, which represents the lock-in state. The condition and thereby the region in the frequency–amplitude parameter space where a general 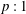 $p:1$ lock-in occurs is then identified. Several important analytical expressions, such as for (1) critical threshold frequency above which lock-in occurs, (2) boundary of lock-in region in the parameter space, that are of direct importance to the design of quieter combustors are obtained. The study also identifies the transition of higher-order
$p:1$ lock-in occurs is then identified. Several important analytical expressions, such as for (1) critical threshold frequency above which lock-in occurs, (2) boundary of lock-in region in the parameter space, that are of direct importance to the design of quieter combustors are obtained. The study also identifies the transition of higher-order 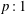 $p:1$ to
$p:1$ to 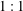 $1:1$ lock-in state, through a series of lock-in and de-lock-in steps, whose occurrence could be verified from future experiments.
$1:1$ lock-in state, through a series of lock-in and de-lock-in steps, whose occurrence could be verified from future experiments.