Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-08T04:33:07.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal scaling law for drag-to-thrust wake transition in flapping foils

Published online by Cambridge University Press:  07 June 2019

N. S. Lagopoulos Open the ORCID record for N. S. Lagopoulos [Opens in a new window] ,
G. D. Weymouth Open the ORCID record for G. D. Weymouth [Opens in a new window]  and
B. Ganapathisubramani Open the ORCID record for B. Ganapathisubramani [Opens in a new window]
N. S. Lagopoulos*
Affiliation:
Aerodynamics and Flight Mechanics Group, University of Southampton, UK
G. D. Weymouth
Affiliation:
Southampton Marine and Maritime Institute, University of Southampton, UK
B. Ganapathisubramani
Affiliation:
Aerodynamics and Flight Mechanics Group, University of Southampton, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

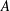Reversed von Kármán streets are responsible for a velocity surplus in the wake of flapping foils, indicating the onset of thrust generation. However, the wake pattern cannot be predicted based solely on the flapping peak-to-peak amplitude $A$ and frequency 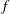$f$ because the transition also depends sensitively on other details of the kinematics. In this work we replace 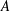$A$ with the cycle-averaged swept trajectory 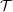${\mathcal{T}}$ of the foil chordline. Two-dimensional simulations are performed for pure heave, pure pitch and a variety of heave-to-pitch coupling. In a phase space of dimensionless 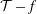${\mathcal{T}}-f$ we show that the drag-to-thrust wake transition of all tested modes occurs for a modified Strouhal 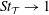$St_{{\mathcal{T}}}\rightarrow 1$. Physically, the product ${\mathcal{T}}f$ expresses the induced velocity of the foil and indicates that propulsive jets occur when this velocity exceeds 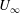$U_{\infty }$. The new metric offers a unique insight into the thrust-producing strategies of biological swimmers and flyers alike, as it directly connects the wake development to the chosen kinematics, enabling a self-similar characterisation of flapping foil propulsion.

JFM classification

Biological Fluid Dynamics: Propulsion Vortex Flows: Vortex shedding Wakes/Jets: Vortex streets
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , R1
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, A., Bohr, T., Schnipper, T. & Walther, J. H. 2017 Wake structure and thrust generation of a flapping foil in two-dimensional flow. J. Fluid Mech. 812, R4.Google Scholar
Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Birnbaum, W. 1924 Das ebene Problem des schlagenden Flügels. Z. Angew. Math. Mech. 4 (4), 277–292.Google Scholar
Bohl, D. G. & Koochesfahani, M. M. 2009 MTV measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency. J. Fluid Mech. 620, 63–88.Google Scholar
Cleaver, D. J., Wang, Z. & Gursul, I. 2012 Bifurcating flows of plunging aerofoils at high Strouhal numbers. J. Fluid Mech. 708, 349–376.Google Scholar
Fish, F. E. & Lauder, G. V. 2006 Passive and active flow control by swimming fishes and mammals. Annu. Rev. Fluid Mech. 38, 193–224.Google Scholar
Godoy-Diana, R., Aider, J. L. & Wesfreid, J. E. 2008 Transitions in the wake of a flapping foil. Phys. Rev. E 77 (1), 016308.Google Scholar
Godoy-Diana, R., Marais, C., Aider, J. L. & Wesfreid, J. E. 2009 A model for the symmetry breaking of the reverse Bénard–von Kármán vortex street produced by a flapping foil. J. Fluid Mech. 622, 23–32.Google Scholar
Koochesfahani, M. M. 1989 Vortical patterns in the wake of an oscillating airfoil. AIAA J. 27 (9), 1200–1205.Google Scholar
Maertens, A. P. & Weymouth, G. D. 2015 Accurate Cartesian-grid simulations of near-body flows at intermediate Reynolds numbers. Comput. Meth. Appl. Mech. Engng 283, 106–129.Google Scholar
Mittal, R. & Balachandar, S. 1995 Effect of threedimensionality on the lift and drag of nominally two-dimensional cylinders. Phys. Fluids 7 (8), 1841–1865.Google Scholar
Platzer, M. & Jones, K. 2008 Flapping wing aerodynamics-progress and challenges. In 44th AIAA Aerospace Sciences Meeting and Exhibit, p. 500. AIAA.Google Scholar
Polet, D. T., Rival, D. E. & Weymouth, G. D. 2015 Unsteady dynamics of rapid perching manoeuvres. J. Fluid Mech. 767, 323–341.Google Scholar
Ramamurti, R. & Sandberg, W. 2001 Computational study of 3D flapping foil flows. In 39th Aerospace Sciences Meeting and Exhibit, p. 605. AIAA.Google Scholar
Read, D. A., Hover, F. S. & Triantafyllou, M. S. 2003 Forces on oscillating foils for propulsion and manoeuvering. J. Fluids Struct. 17 (1), 163–183.Google Scholar
Streitlien, K. & Triantafyllou, G. S. 1998 On thrust estimates for flapping foils. J. Fluids Struct. 12 (1), 47–55.Google Scholar
Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. 2003 Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 425 (6959), 707.Google Scholar
Thiria, B., Goujon-Durand, S. & Wesfreid, J. E. 2006 The wake of a cylinder performing rotary oscillations. J. Fluid Mech. 560, 123–147.Google Scholar
Triantafyllou, G. S., Triantafyllou, M. S. & Grosenbaugh, M. A. 1993 Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 7 (2), 205–224.Google Scholar
Triantafyllou, M. S., Techet, A. H. & Hover, F. S. 2004 Review of experimental work in biomimetic foils. IEEE J. Ocean. Engng 29 (3), 585–594.Google Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Gopalkrishnan, R. 1991 Wake mechanics for thrust generation in oscillating foils. Phys. Fluids A 3 (12), 2835–2837.Google Scholar
Vial, M., Bellon, L. & Hernández, R. H. 2004 Mechanical forcing of the wake of a flat plate. Exp. Fluids 37 (2), 168–176.Google Scholar
Von Kármán, T. 1935 General aerodynamic theory-perfect fluids. Aerodynamic Theory 2, 346–349.Google Scholar
Wang, Z. J. 2005 Dissecting insect flight. Annu. Rev. Fluid Mech. 37 (1), 183–210.Google Scholar
Weymouth, G. D. & Yue, D. K. P. 2011 Boundary data immersion method for Cartesian-grid simulations of fluid–body interaction problems. J. Comput. Phys. 230 (16), 6233–6247.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.Google Scholar