1 Introduction
A thorough knowledge of the dynamic interactions between fluid interfaces is paramount to a deeper understanding of a variety of natural processes and engineering applications, such as combustion, microfluidic coating, food processing and many others. The coalescence and/or repulsion between droplets or bubbles can be traced to the hydrodynamic drag originating from the relative motion of two fluid interfaces in near contact (Barnocky & Davis Reference Barnocky and Davis1989; Davis, Schonberg & Rallison Reference Davis, Schonberg and Rallison1989; Shi, Brenner & Nagel Reference Shi, Brenner and Nagel1994; Mani, Mandre & Brenner Reference Mani, Mandre and Brenner2010; Rubin et al. Reference Rubin, Tulchinsky, Gat and Bercovici2017), and to the combined action of nanoscale attractive and/or repulsive forces, such as van der Waals and electrostatic forces, steric interactions, hydration repulsion and depletion attraction (Bergeron Reference Bergeron1999; Stubenrauch & Von Klitzing Reference Stubenrauch and Von Klitzing2003).
A wide body of theoretical and experimental work has elucidated the complex nature of the near-contact interactions which develop within intervening liquid films: from the pioneering works of Gibbs and Marangoni on the thermodynamics of liquid thin films (see Bergeron (Reference Bergeron1999) for a comprehensive review) to the separate work of Derjaguin and Overbeek (Derjaguin Reference Derjaguin1940; Verwey, Overbeek & Overbeek Reference Verwey, Overbeek and Overbeek1999) which culminated in the joint DLVO theory (after its founders, Derjaguin, Landau, Verwey and Overbeek).
These seminal works laid down the foundations for describing a broad variety of complex flowing systems, such as colloids, foams and emulsions, as well as flowing collections of droplets and bubbles characterized by highly ordered and uniform, crystal-like structures, now known as soft flowing crystals (Garstecki & Whitesides Reference Garstecki and Whitesides2006; Marmottant & Raven Reference Marmottant and Raven2009).
From a numerical standpoint, the direct introduction of near-interaction forces at a molecular level reflects the need of solving simultaneously six spatial decades: from millimetres, i.e. the typical size of microfluidic devices, down to nanometres (and below), namely the relevant spatial scale of contact forces. This is far beyond the capability of any foreseeable computer (Montessori, Lauricella & Succi Reference Montessori, Lauricella and Succi2019), hence placing a high premium on coarse-grained, mesoscale representations of near-contact forces, capable of retaining computational viability without compromising the essential physics.
Of course, the success of such mesoscale strategy hinges crucially on the universality of the underlying physics, i.e. its dependence on suitable dimensionless parameters measuring the relative strength of the interactions, rather than on the details and strength of the interactions themselves (Succi Reference Succi2015). Failing such universality, a genuine microscopic approach cannot be helped, thus hampering the possibility to reach up to the scales of the full device.
In the lattice Boltzmann (LB) framework, immiscible fluids were first modelled by Gunstensen et al. (Reference Gunstensen, Rothman, Zaleski and Zanetti1991). These authors developed an LB model, augmented with a forcing term in accordance with the local colour gradient, giving rise to the interface tension and a segregation step. In Latva-Kokko & Rothman (Reference Latva-Kokko and Rothman2005), the authors corrected the segregation rule proposed by Gunstensen, to avoid the pinning problem that affected the Gunstensen model, allowing the fluids to moderately mix and to keep the colour distribution symmetric with respect to the colour gradient. The reason for lattice pinning is that at the sites where it happens, all of the particles of one kind are sent in the same direction and hence they cannot move from one site to another. More recently the model was further improved to simulate high density and viscosity ratio (Leclaire, Reggio & Trépanier Reference Leclaire, Reggio and Trépanier2012; Leclaire et al. Reference Leclaire, Parmigiani, Malaspinas, Chopard and Latt2017; Saito, Abe & Koyama Reference Saito, Abe and Koyama2017).
In addition to this, there have been several attempts to model interface interactions in amphiphilic fluids within the LB framework (see for example Chen, Boghosian & Coveney (Reference Chen, Boghosian and Coveney2000), Nekovee et al. (Reference Nekovee, Coveney, Chen and Boghosian2000), Love, Coveney & Boghosian (Reference Love, Coveney and Boghosian2001)). These models aim at directly simulating the effect of a surfactant by evolving two sets of distribution functions, allowing us to take into account the presence of an amphiphilic fluid at the interface between two liquid phases. For a comprehensive review of multiphase and multicomponent LB models (Shan & Chen Reference Shan and Chen1993; Swift, Osborn & Yeomans Reference Swift, Osborn and Yeomans1995; He, Shan & Doolen Reference He, Shan and Doolen1998; Guo & Zhao Reference Guo and Zhao2005; Philippi et al. Reference Philippi, Mattila, Siebert, dos Santos, Júnior and Surmas2012), the interested reader is referred to Huang, Sukop & Lu (Reference Huang, Sukop and Lu2015).
In this paper, we present an LB-based approach for multicomponent flows, based on the colour-gradient model (Leclaire et al. Reference Leclaire, Reggio and Trépanier2012), augmented with an additional forcing term which is aimed at representing the effects of the near-contact forces operating at the fluid interface level. The proposed model is shown to accurately capture the collision outcomes between bouncing droplets for different values of the governing parameters, to predict the effective viscosity of dense emulsions in channels and to effectively simulate the evolution of soft flowing crystals in flow focuser devices.
The paper is organized as follows. In § 2 the LB equation with the Bhatnagar–Gross–Krook collisional operator is described, together with the colour-gradient model and the regularization algorithm for simulating multicomponent fluids. The augmented LB model for repulsive near-contact interactions is discussed in detail in § 2.2. Section 3 collects the main results of the paper. Finally, a summary is reported in § 4.
2 Method
Lattice Boltzmann models for non-ideal fluids come mainly in two families. The first one is based on heuristic assumptions (Körner et al. Reference Körner, Thies, Hofmann, Thürey and Rüde2005; Becker et al. Reference Becker, Junk, Kehrwald, Thömmes and Yang2009; Leclaire et al. Reference Leclaire, Reggio and Trépanier2012, Reference Leclaire, Parmigiani, Malaspinas, Chopard and Latt2017; Montessori et al. Reference Montessori, Lauricella, La Rocca, Succi, Stolovicki, Ziblat and Weitz2018a ) while the second one builds on the projection of the kinetic equation on a discrete set of microscopic velocities (Shan & Chen Reference Shan and Chen1993; Swift et al. Reference Swift, Osborn and Yeomans1995; He et al. Reference He, Shan and Doolen1998; Guo & Zhao Reference Guo and Zhao2005; Philippi et al. Reference Philippi, Mattila, Siebert, dos Santos, Júnior and Surmas2012; Montessori et al. Reference Montessori, Prestininzi, La Rocca and Succi2017). For a more exhaustive review, see Huang et al. (Reference Huang, Sukop and Lu2015), Succi (Reference Succi2018). In the following we provide a brief introduction to the one which we found most suitable for the description of flowing crystals, namely the regularized colour-gradient method (Montessori et al. Reference Montessori, Lauricella, La Rocca, Succi, Stolovicki, Ziblat and Weitz2018a ).
2.1 Regularized colour-gradient lattice Boltzmann model
In the colour-gradient LB for multicomponent flows, two sets of distribution functions are needed to track the evolution of the two fluid components, which occurs via a streaming-collision algorithm (for a comprehensive review on the LB method, please refer to Krüger et al. (Reference Krüger, Kusumaatmaja, Kuzmin, Shardt, Silva and Viggen2017), Succi (Reference Succi2018)),
where
![]() $f_{i}^{k}$
is the discrete distribution function, representing the probability of finding a particle of the
$f_{i}^{k}$
is the discrete distribution function, representing the probability of finding a particle of the
![]() $k$
th component at position
$k$
th component at position
![]() $\boldsymbol{x}$
and time
$\boldsymbol{x}$
and time
![]() $t$
with discrete velocity
$t$
with discrete velocity
![]() $\boldsymbol{c}_{i}$
, where
$\boldsymbol{c}_{i}$
, where
![]() $i$
is the index running over the lattice discrete directions
$i$
is the index running over the lattice discrete directions
![]() $i=0,\ldots ,b$
, where
$i=0,\ldots ,b$
, where
![]() $b=26$
for a three-dimensional 27 speed lattice (D3Q27). The lattice time step
$b=26$
for a three-dimensional 27 speed lattice (D3Q27). The lattice time step
![]() $\unicode[STIX]{x0394}t$
has been taken as
$\unicode[STIX]{x0394}t$
has been taken as
![]() $1$
(in lattice units) for convenience, which is a common practice in the LB literature (see Succi (Reference Succi2018)). The density
$1$
(in lattice units) for convenience, which is a common practice in the LB literature (see Succi (Reference Succi2018)). The density
![]() $\unicode[STIX]{x1D70C}^{k}$
of the
$\unicode[STIX]{x1D70C}^{k}$
of the
![]() $k$
th component is given by the zeroth moment of the distribution functions,
$k$
th component is given by the zeroth moment of the distribution functions,
The total fluid density is given by
![]() $\unicode[STIX]{x1D70C}=\sum _{k}\unicode[STIX]{x1D70C}^{k}$
, while the total momentum of the mixture is defined as the sum of the linear momentum of the two components,
$\unicode[STIX]{x1D70C}=\sum _{k}\unicode[STIX]{x1D70C}^{k}$
, while the total momentum of the mixture is defined as the sum of the linear momentum of the two components,
The collision operator can be split into three parts (Gunstensen et al. Reference Gunstensen, Rothman, Zaleski and Zanetti1991; Leclaire et al. Reference Leclaire, Reggio and Trépanier2012, Reference Leclaire, Parmigiani, Malaspinas, Chopard and Latt2017),
In the above,
![]() $(\unicode[STIX]{x1D6FA}_{i}^{k})^{(1)}$
stands for the standard collisional relaxation (Succi Reference Succi2001) which reads
$(\unicode[STIX]{x1D6FA}_{i}^{k})^{(1)}$
stands for the standard collisional relaxation (Succi Reference Succi2001) which reads
![]() $(\unicode[STIX]{x1D6FA}_{i}^{k})^{(1)}=\unicode[STIX]{x1D714}_{eff}(f_{i}^{k,eq}-f_{i}^{k})$
, where
$(\unicode[STIX]{x1D6FA}_{i}^{k})^{(1)}=\unicode[STIX]{x1D714}_{eff}(f_{i}^{k,eq}-f_{i}^{k})$
, where
![]() $\unicode[STIX]{x1D714}_{eff}=2/(6\bar{\unicode[STIX]{x1D708}}-1)$
is the effective relaxation parameter with
$\unicode[STIX]{x1D714}_{eff}=2/(6\bar{\unicode[STIX]{x1D708}}-1)$
is the effective relaxation parameter with
![]() $\bar{\unicode[STIX]{x1D708}}$
the viscosity at the interface between the two fluids which is computed as
$\bar{\unicode[STIX]{x1D708}}$
the viscosity at the interface between the two fluids which is computed as
![]() $1/\bar{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D70C}_{1}/(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2}))(1/\unicode[STIX]{x1D708}_{1})+(\unicode[STIX]{x1D70C}_{2}/(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2}))(1/\unicode[STIX]{x1D708}_{2})$
(
$1/\bar{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D70C}_{1}/(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2}))(1/\unicode[STIX]{x1D708}_{1})+(\unicode[STIX]{x1D70C}_{2}/(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2}))(1/\unicode[STIX]{x1D708}_{2})$
(
![]() $\unicode[STIX]{x1D708}_{1}$
and
$\unicode[STIX]{x1D708}_{1}$
and
![]() $\unicode[STIX]{x1D708}_{2}$
are the kinematic viscosities of the two fluids in the bulk). The equilibrium distribution function of the
$\unicode[STIX]{x1D708}_{2}$
are the kinematic viscosities of the two fluids in the bulk). The equilibrium distribution function of the
![]() $k$
th component
$k$
th component
![]() $f_{i}^{k,eq}$
is given by a low Mach, second-order, expansion of a local Maxwellian, namely
$f_{i}^{k,eq}$
is given by a low Mach, second-order, expansion of a local Maxwellian, namely
![]() $f_{i}^{k,eq}=w_{i}\unicode[STIX]{x1D70C}^{k}(1+(\boldsymbol{c}_{\boldsymbol{i}}\boldsymbol{\cdot }\boldsymbol{u}/c_{s}^{2})+((\boldsymbol{c}_{\boldsymbol{i}}\boldsymbol{\cdot }\boldsymbol{u})^{2}/2c_{s}^{4})-(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}/2c_{s}^{2}))$
.
$f_{i}^{k,eq}=w_{i}\unicode[STIX]{x1D70C}^{k}(1+(\boldsymbol{c}_{\boldsymbol{i}}\boldsymbol{\cdot }\boldsymbol{u}/c_{s}^{2})+((\boldsymbol{c}_{\boldsymbol{i}}\boldsymbol{\cdot }\boldsymbol{u})^{2}/2c_{s}^{4})-(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}/2c_{s}^{2}))$
.
Here
![]() $(\unicode[STIX]{x1D6FA}_{i}^{k})^{(2)}$
is the perturbation step (Gunstensen et al.
Reference Gunstensen, Rothman, Zaleski and Zanetti1991), which contributes to the build-up of an interfacial tension. Finally,
$(\unicode[STIX]{x1D6FA}_{i}^{k})^{(2)}$
is the perturbation step (Gunstensen et al.
Reference Gunstensen, Rothman, Zaleski and Zanetti1991), which contributes to the build-up of an interfacial tension. Finally,
![]() $(\unicode[STIX]{x1D6FA}_{i}^{k})^{(3)}$
is the recolouring step (Gunstensen et al.
Reference Gunstensen, Rothman, Zaleski and Zanetti1991; Latva-Kokko & Rothman Reference Latva-Kokko and Rothman2005), which promotes the segregation between species, so as to minimize their mutual diffusion.
$(\unicode[STIX]{x1D6FA}_{i}^{k})^{(3)}$
is the recolouring step (Gunstensen et al.
Reference Gunstensen, Rothman, Zaleski and Zanetti1991; Latva-Kokko & Rothman Reference Latva-Kokko and Rothman2005), which promotes the segregation between species, so as to minimize their mutual diffusion.
In order to reproduce the correct form of the stress tensor (Landau & Lifshitz Reference Landau and Lifshitz1959), the perturbation operator can be constructed by exploiting the concept of the continuum surface force (Brackbill, Kothe & Zemach Reference Brackbill, Kothe and Zemach1992). Firstly, the perturbation operator must satisfy the following conservation constraints,
By performing a Chapman–Enskog expansion, it can be shown that the hydrodynamic limit of (2.1) is represented by a set of equations for the conservation of mass and linear momentum,
where
![]() $p=\sum _{k}p_{k}$
is the pressure and
$p=\sum _{k}p_{k}$
is the pressure and
![]() $\unicode[STIX]{x1D708}=c_{s}^{2}(\unicode[STIX]{x1D70F}-1/2)$
is the kinematic viscosity of the mixture, with
$\unicode[STIX]{x1D708}=c_{s}^{2}(\unicode[STIX]{x1D70F}-1/2)$
is the kinematic viscosity of the mixture, with
![]() $\unicode[STIX]{x1D70F}$
the single relaxation time and
$\unicode[STIX]{x1D70F}$
the single relaxation time and
![]() $c_{s}=1/\sqrt{3}$
the sound speed of the model (Succi Reference Succi2001; Krüger et al.
Reference Krüger, Kusumaatmaja, Kuzmin, Shardt, Silva and Viggen2017).
$c_{s}=1/\sqrt{3}$
the sound speed of the model (Succi Reference Succi2001; Krüger et al.
Reference Krüger, Kusumaatmaja, Kuzmin, Shardt, Silva and Viggen2017).
Note that the divergence of the stress tensor (last term in (2.8)), which is responsible for the build-up of surface tension, acts only at the interface between the fluids (see (2.11)).
The stress tensor in the momentum equation is given by
The surface stress boundary condition at the interface between two fluids can be expressed as follows (Landau & Lifshitz Reference Landau and Lifshitz1959; Brackbill et al. Reference Brackbill, Kothe and Zemach1992):
where,
![]() $\unicode[STIX]{x1D644}$
is the identity tensor,
$\unicode[STIX]{x1D644}$
is the identity tensor,
![]() $\unicode[STIX]{x1D70E}$
is the surface tension coefficient (with dimensions of force per unit area),
$\unicode[STIX]{x1D70E}$
is the surface tension coefficient (with dimensions of force per unit area),
![]() $\boldsymbol{n}$
is the unit normal to the interface,
$\boldsymbol{n}$
is the unit normal to the interface,
![]() $\unicode[STIX]{x1D64F}=-p\unicode[STIX]{x1D644}+\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$
is the stress tensor of the
$\unicode[STIX]{x1D64F}=-p\unicode[STIX]{x1D644}+\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$
is the stress tensor of the
![]() $k$
th component and
$k$
th component and
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{n}$
is the local curvature of the fluid interface.
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{n}$
is the local curvature of the fluid interface.
The local stress jump at the interface can be induced by adding an interfacial volume force
![]() $\boldsymbol{F}(\boldsymbol{x},t)$
(Liu, Valocchi & Kang Reference Liu, Valocchi and Kang2012),
$\boldsymbol{F}(\boldsymbol{x},t)$
(Liu, Valocchi & Kang Reference Liu, Valocchi and Kang2012),
In the above,
![]() $\unicode[STIX]{x1D6FF}_{I}=(1/2)|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}|$
is an index function which explicitly localizes the force on the interface and
$\unicode[STIX]{x1D6FF}_{I}=(1/2)|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}|$
is an index function which explicitly localizes the force on the interface and
![]() $\unicode[STIX]{x1D6E9}=(\unicode[STIX]{x1D70C}^{1}-\unicode[STIX]{x1D70C}^{2})/(\unicode[STIX]{x1D70C}^{1}+\unicode[STIX]{x1D70C}^{2})$
is the phase field (Liu et al.
Reference Liu, Valocchi and Kang2012). The normal to the interface can be approximated by the gradient of the phase field,
$\unicode[STIX]{x1D6E9}=(\unicode[STIX]{x1D70C}^{1}-\unicode[STIX]{x1D70C}^{2})/(\unicode[STIX]{x1D70C}^{1}+\unicode[STIX]{x1D70C}^{2})$
is the phase field (Liu et al.
Reference Liu, Valocchi and Kang2012). The normal to the interface can be approximated by the gradient of the phase field,
![]() $\boldsymbol{n}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}/|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}|$
.
$\boldsymbol{n}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}/|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}|$
.
Since the perturbation operator is responsible for generating interfacial tension, the following relation must hold
By choosing (Leclaire et al.
Reference Leclaire, Reggio and Trépanier2012)
![]() $(\unicode[STIX]{x1D6FA}_{i}^{k})^{(2)}=(A_{k}/2)|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}|[w_{i}((\boldsymbol{c}_{i}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9})^{2}/|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}|^{2})-B_{i}]$
, substituting it into (2.5) and (2.12) and by imposing that the set
$(\unicode[STIX]{x1D6FA}_{i}^{k})^{(2)}=(A_{k}/2)|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}|[w_{i}((\boldsymbol{c}_{i}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9})^{2}/|\unicode[STIX]{x1D735}\unicode[STIX]{x1D6E9}|^{2})-B_{i}]$
, substituting it into (2.5) and (2.12) and by imposing that the set
![]() $B_{i}$
must satisfy the following isotropy constraints
$B_{i}$
must satisfy the following isotropy constraints
we obtain an equation for the surface tension of the model
The above relation shows a direct link between the surface tension and the parameter
![]() $A=A_{1}+A_{2}$
(
$A=A_{1}+A_{2}$
(
![]() $A_{1}=A_{2}$
). In actual practice, after choosing the viscosity of the two components and the surface tension of the model, at each time step, one locally computes the
$A_{1}=A_{2}$
). In actual practice, after choosing the viscosity of the two components and the surface tension of the model, at each time step, one locally computes the
![]() $A=A_{1}+A_{2}$
coefficient by using the formula reported in (2.14).
$A=A_{1}+A_{2}$
coefficient by using the formula reported in (2.14).
It is worth noting that, in this work, a fourth-order isotropic discrete gradient operator on a 27 points stencil is employed (for details please refer to Leclaire et al. (Reference Leclaire, Parmigiani, Malaspinas, Chopard and Latt2017)).
As pointed out above, the perturbation operator generates an interfacial tension in compliance with the capillary-stress tensor of the Navier–Stokes equations for a multicomponent fluid system.
Nonetheless, the perturbation operator alone does not guarantee the immiscibility of different fluid components. For this reason, a further step is needed (i.e. the recolouring step) to minimize the mutual diffusion between components.
Following the work of Latva-Kokko & Rothman (Reference Latva-Kokko and Rothman2005), the recolouring operator for the two sets of distributions takes the following form:
where,
![]() $f_{i}^{\ast }=\sum _{k}f_{i}^{k,\ast }$
denotes the set of post-perturbation distributions,
$f_{i}^{\ast }=\sum _{k}f_{i}^{k,\ast }$
denotes the set of post-perturbation distributions,
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}^{1}+\unicode[STIX]{x1D70C}^{2}$
,
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}^{1}+\unicode[STIX]{x1D70C}^{2}$
,
![]() $\cos \unicode[STIX]{x1D719}_{i}$
is the angle between the phase field gradient and the
$\cos \unicode[STIX]{x1D719}_{i}$
is the angle between the phase field gradient and the
![]() $i$
th lattice vector and
$i$
th lattice vector and
![]() $f_{i}^{eq,0}=f_{i}(\unicode[STIX]{x1D70C},\boldsymbol{u}=0)^{eq}=\sum _{k}f_{i}^{k}(\unicode[STIX]{x1D70C},\boldsymbol{u}=0)^{eq}$
is the total zero-velocity equilibrium distribution function (Leclaire et al.
Reference Leclaire, Reggio and Trépanier2012).
$f_{i}^{eq,0}=f_{i}(\unicode[STIX]{x1D70C},\boldsymbol{u}=0)^{eq}=\sum _{k}f_{i}^{k}(\unicode[STIX]{x1D70C},\boldsymbol{u}=0)^{eq}$
is the total zero-velocity equilibrium distribution function (Leclaire et al.
Reference Leclaire, Reggio and Trépanier2012).
Note that the coefficient
![]() $\unicode[STIX]{x1D6FD}$
in the above expressions is a free parameter which can be used to tune the interface width, thus playing the role of an inverse diffusion length scale (Latva-Kokko & Rothman Reference Latva-Kokko and Rothman2005). We wish to point out that the present model is employed to simulate droplet-based microfluidic applications which are often characterized by very small
$\unicode[STIX]{x1D6FD}$
in the above expressions is a free parameter which can be used to tune the interface width, thus playing the role of an inverse diffusion length scale (Latva-Kokko & Rothman Reference Latva-Kokko and Rothman2005). We wish to point out that the present model is employed to simulate droplet-based microfluidic applications which are often characterized by very small
![]() $We$
,
$We$
,
![]() $Re$
and
$Re$
and
![]() $Ca$
numbers (i.e. much smaller than one). Hence, by considering typical flow speeds of
$Ca$
numbers (i.e. much smaller than one). Hence, by considering typical flow speeds of
![]() $10^{-3}{-}10^{-2}lu/step$
the
$10^{-3}{-}10^{-2}lu/step$
the
![]() $u^{3}$
error contribution is of the order
$u^{3}$
error contribution is of the order
![]() $O(10^{-12}{-}10^{-9})$
, which reflects in a very negligible compressibility errors. It is important to note that, following the work of Leclaire et al. (Reference Leclaire, Reggio and Trépanier2012), in this work we perform the entire collision step (collision+perturbation+recolouring steps) on two separate distributions, this at variance with the works of Gunstensen et al. (Reference Gunstensen, Rothman, Zaleski and Zanetti1991) and Latva-Kokko & Rothman (Reference Latva-Kokko and Rothman2005), in which the collision and perturbation are written in terms of the blind distribution
$O(10^{-12}{-}10^{-9})$
, which reflects in a very negligible compressibility errors. It is important to note that, following the work of Leclaire et al. (Reference Leclaire, Reggio and Trépanier2012), in this work we perform the entire collision step (collision+perturbation+recolouring steps) on two separate distributions, this at variance with the works of Gunstensen et al. (Reference Gunstensen, Rothman, Zaleski and Zanetti1991) and Latva-Kokko & Rothman (Reference Latva-Kokko and Rothman2005), in which the collision and perturbation are written in terms of the blind distribution
![]() $f=f^{1}+f^{2}$
.
$f=f^{1}+f^{2}$
.
The colour-gradient LB scheme is further regularized by filtering out the high-order non-hydrodynamic (ghost) modes, emerging after the streaming step (see Latt & Chopard (Reference Latt and Chopard2006), Zhang, Shan & Chen (Reference Zhang, Shan and Chen2006), Montessori et al. (Reference Montessori, Prestininzi, La Rocca and Succi2015), Montessori et al. (Reference Montessori, Prestininzi, La Rocca, Falcucci, Succi and Kaxiras2016), Coreixas et al. (Reference Coreixas, Wissocq, Puigt, Boussuge and Sagaut2017), Mattila, Philippi & Hegele (Reference Mattila, Philippi and Hegele2017), Hegele et al. (Reference Hegele, Scagliarini, Sbragaglia, Mattila, Philippi, Puleri, Gounley and Randles2018) for further details).
Indeed, it was noted that sizeable non-isotropic effects arise in the model (Montessori et al.
Reference Montessori, Lauricella, La Rocca, Succi, Stolovicki, Ziblat and Weitz2018a
), whenever the LB scheme is under-relaxed (
![]() $\unicode[STIX]{x1D70F}\geqslant 1$
). As a consequence, we exploit the regularization procedure in order to recover the loss of isotropy by suppressing the non-hydrodynamic modes (Benzi, Succi & Vergassola Reference Benzi, Succi and Vergassola1992; Montessori et al.
Reference Montessori, Lauricella, La Rocca, Succi, Stolovicki, Ziblat and Weitz2018a
,Reference Montessori, Lauricella, Succi, Stolovicki and Weitz
b
). For the sake of clarity, here we report a pseudocode of the regularization procedure employed in our simulations:
$\unicode[STIX]{x1D70F}\geqslant 1$
). As a consequence, we exploit the regularization procedure in order to recover the loss of isotropy by suppressing the non-hydrodynamic modes (Benzi, Succi & Vergassola Reference Benzi, Succi and Vergassola1992; Montessori et al.
Reference Montessori, Lauricella, La Rocca, Succi, Stolovicki, Ziblat and Weitz2018a
,Reference Montessori, Lauricella, Succi, Stolovicki and Weitz
b
). For the sake of clarity, here we report a pseudocode of the regularization procedure employed in our simulations:

where
![]() $f_{l}^{pc,m}(i,j,k)$
is the set of post-collision distribution functions of the
$f_{l}^{pc,m}(i,j,k)$
is the set of post-collision distribution functions of the
![]() $m$
th component,
$m$
th component,
![]() $f_{l}^{neq,m}(i,j,k)$
is the non-equilibrium part of
$f_{l}^{neq,m}(i,j,k)$
is the non-equilibrium part of
![]() $f_{l}^{pc,m}(i,j,k)$
,
$f_{l}^{pc,m}(i,j,k)$
,
![]() $p_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{m}$
are the components of the non-equilibrium part of the momentum flux tensor,
$p_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{m}$
are the components of the non-equilibrium part of the momentum flux tensor,
![]() $D$
stands for the fluid domain (
$D$
stands for the fluid domain (
![]() $(i,j,k)\in D$
is a lattice node in the fluid domain) and
$(i,j,k)\in D$
is a lattice node in the fluid domain) and
![]() $f_{l}^{reg}(i,j,k)$
is the regularized set of post-collision distribution functions.
$f_{l}^{reg}(i,j,k)$
is the regularized set of post-collision distribution functions.
In the next subsection, we show how to include the effect of repulsive near-contact interactions, directly within the LB framework, by augmenting the regularized colour-gradient model with a forcing term aimed at coarse graining the near-contact forces at the fluid surface.
2.2 Augmented LB model for repulsive near-contact interactions
The stress-jump condition across a fluid interface is augmented with a repulsive term aimed at providing a mesoscale representation of all the repulsive near-contact forces (i.e. van der Waals, electrostatic, steric and hydration repulsion) acting on much smaller scales (
![]() ${\sim}O(1~\text{nm})$
) than those resolved on the lattice (typically well above hundreds of nanometres). It takes the following form:
${\sim}O(1~\text{nm})$
) than those resolved on the lattice (typically well above hundreds of nanometres). It takes the following form:
where
![]() $\unicode[STIX]{x03C0}[h(\boldsymbol{x})]$
is responsible for the repulsion between neighbouring fluid interfaces,
$\unicode[STIX]{x03C0}[h(\boldsymbol{x})]$
is responsible for the repulsion between neighbouring fluid interfaces,
![]() $h(\boldsymbol{x})$
being the distance along the normal
$h(\boldsymbol{x})$
being the distance along the normal
![]() $\boldsymbol{n}$
, between locations
$\boldsymbol{n}$
, between locations
![]() $\boldsymbol{x}$
and
$\boldsymbol{x}$
and
![]() $\boldsymbol{y}=\boldsymbol{x}+h\boldsymbol{n}$
at the two interfaces, respectively (see figure 1).
$\boldsymbol{y}=\boldsymbol{x}+h\boldsymbol{n}$
at the two interfaces, respectively (see figure 1).
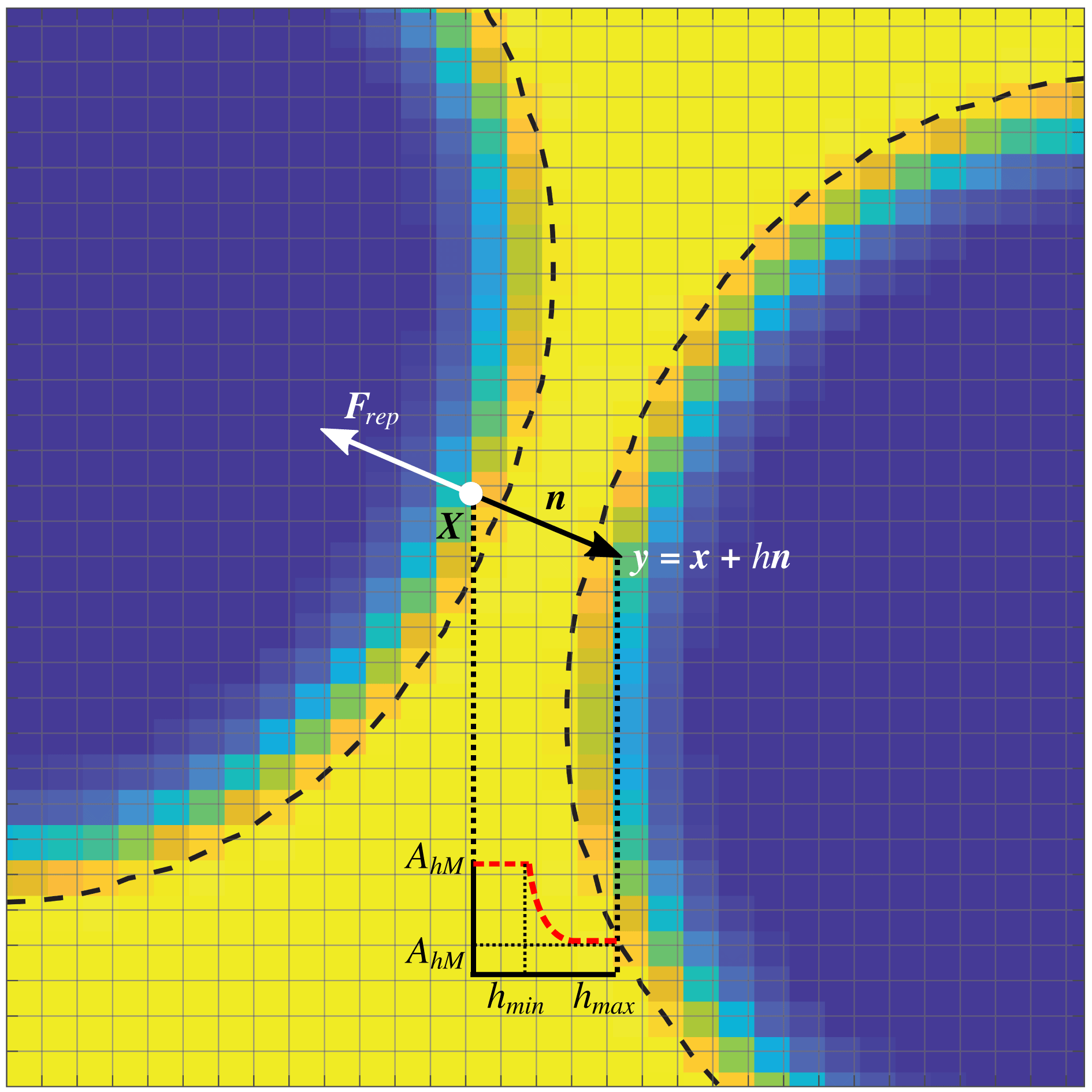
Figure 1. Graphical representation of the near interaction between two impacting droplets.
The above expression can be rewritten in the following form (Li Reference Li2016):
in which
![]() $\unicode[STIX]{x1D6FB}_{s}$
is used to identify the gradient tangent to the interface.
$\unicode[STIX]{x1D6FB}_{s}$
is used to identify the gradient tangent to the interface.
By neglecting any variation of the surface tension along the interface, we can approximate
![]() $\unicode[STIX]{x1D64F}=-p\unicode[STIX]{x1D644}$
(Brackbill et al.
Reference Brackbill, Kothe and Zemach1992) and the above equation takes the following form:
$\unicode[STIX]{x1D64F}=-p\unicode[STIX]{x1D644}$
(Brackbill et al.
Reference Brackbill, Kothe and Zemach1992) and the above equation takes the following form:
By projecting the equation along the normal to the surface, we obtain the extended Young–Laplace equation (Williams & Davis Reference Williams and Davis1982; Chan, Klaseboer & Manica Reference Chan, Klaseboer and Manica2011):
The additional term can be readily included within the LB framework, by adding a forcing term acting only on the fluid interfaces in near contact, namely,
In the above,
![]() $A_{h}[h(\boldsymbol{x})]$
is the parameter controlling the strength (force per unit volume) of the near-contact interactions (please refer to the sketch in figure 1).
$A_{h}[h(\boldsymbol{x})]$
is the parameter controlling the strength (force per unit volume) of the near-contact interactions (please refer to the sketch in figure 1).
In this work,
![]() $A_{h}$
is set to a constant value (
$A_{h}$
is set to a constant value (
![]() $A_{hM}$
) if
$A_{hM}$
) if
![]() $h<h_{min}$
and then decreases as
$h<h_{min}$
and then decreases as
![]() ${\sim}h^{-3}$
, as shown in figure 1, although other choices are certainly possible.
${\sim}h^{-3}$
, as shown in figure 1, although other choices are certainly possible.
The near-contact force has been defined solely as a function of the distance between two fluid interfaces. Nonetheless, it could be easily extended to take into account local variations due to the effect of spontaneous migrations of the surfactant along the fluid interface (Gupta, Badruddoza & Doyle Reference Gupta, Badruddoza and Doyle2017).
The addition of the repulsive force, naturally leads to the following (extended) conservation law for the momentum equation,
This is the Navier–Stokes equation for a multicomponent system augmented with a surface-localized repulsive term, expressed through the potential function
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x03C0}$
.
$\unicode[STIX]{x1D735}\unicode[STIX]{x03C0}$
.
There have been other attempts to model interface interactions in amphiphilic fluids in the literature (see for example Chen et al. (Reference Chen, Boghosian and Coveney2000), Nekovee et al. (Reference Nekovee, Coveney, Chen and Boghosian2000), Love et al. (Reference Love, Coveney and Boghosian2001)). These models aim at directly simulating the effect of a surfactant by evolving two sets of distribution functions, allowing us to take into account the presence of an amphiphilic fluid at the interface between two liquid phases. Indeed, the propagation of the amphiphilic molecules is described as a set of LB equations, one for the distribution function and one for the relaxation of the average dipole vector to its local equilibrium orientation. Halliday, Hollis & Care (Reference Halliday, Hollis and Care2007) and Spencer, Halliday & Care (Reference Spencer, Halliday and Care2010) extended the colour-gradient model to any number of components. This method makes use of a set of distributions for each immiscible fluid species. More recently, Wöhrwag et al. (Reference Wöhrwag, Semprebon, Moqaddam, Karlin and Kusumaatmaja2018) proposed a thermodynamically consistent free energy model for fluid flows comprised of one gas and two liquid components using the entropic LB scheme.
The standpoint of our work is quite different in that the repulsive action of a surfactant, arising when two interfaces come in close contact, is taken into account by introducing a repulsive forcing term localized at the interface of the two fluids. Importantly, this just requires two distributions functions regardless of the number of droplets.
To conclude, the extended approach still holds to a continuum description of the interface dynamics, with the governing equations modified only by the presence of a distributed body force, which can heuristically be interpreted as a coarse-grained version of the short-range molecular forces acting at the nanometre and sub-nanometre scales.
3 Numerical results
In this section we test the extended LB model on three applications namely, head-on and off-axis collisions between two bouncing droplets, pressure-driven flow of a dense emulsion in a channel and the formation of soft flowing crystals in a microfluidic flow focuser.
3.1 Droplets coalescence
Here we first test the ability of the colour-gradient LB model to capture the physics of the coalescence process between two equally sized droplets. The simulation set-up consists of a three-dimensional fully periodic box (
![]() $160\times 100\times 121$
) in which two liquid droplets of radius
$160\times 100\times 121$
) in which two liquid droplets of radius
![]() $R=30$
, surrounded by a dispersed fluid of the same density, are placed at close distance. The surface tension of the mixture was fixed at a constant value,
$R=30$
, surrounded by a dispersed fluid of the same density, are placed at close distance. The surface tension of the mixture was fixed at a constant value,
![]() $\unicode[STIX]{x1D70E}=0.01$
while the surface tension of the two fluids was varied from
$\unicode[STIX]{x1D70E}=0.01$
while the surface tension of the two fluids was varied from
![]() $\unicode[STIX]{x1D708}=0.05$
to
$\unicode[STIX]{x1D708}=0.05$
to
![]() $\unicode[STIX]{x1D708}=0.15$
. The viscosity ratio between the droplets and the surrounding phase has been set to unity, and all the physical quantities are reported in lattice units. As shown in figure 2(a–c), a liquid bridge forms between the two droplets. As pointed out in Eggers, Lister & Stone (Reference Eggers, Lister and Stone1999) the coalescence process in the early stage is so fast that only a fraction of the fluid caught in the narrow gap between the two spheres is able to escape, while the rest accumulates in a ‘bubble’ which forms at the meniscus. The simulations predict the formation of such a bubble, which remains trapped between the two coalescing droplets. To be more quantitative, we measured the normalized radius of the liquid bridge,
$\unicode[STIX]{x1D708}=0.15$
. The viscosity ratio between the droplets and the surrounding phase has been set to unity, and all the physical quantities are reported in lattice units. As shown in figure 2(a–c), a liquid bridge forms between the two droplets. As pointed out in Eggers, Lister & Stone (Reference Eggers, Lister and Stone1999) the coalescence process in the early stage is so fast that only a fraction of the fluid caught in the narrow gap between the two spheres is able to escape, while the rest accumulates in a ‘bubble’ which forms at the meniscus. The simulations predict the formation of such a bubble, which remains trapped between the two coalescing droplets. To be more quantitative, we measured the normalized radius of the liquid bridge,
![]() $r_{b}/R$
, as a function of the square root of the non-dimensional time
$r_{b}/R$
, as a function of the square root of the non-dimensional time
![]() $t/\unicode[STIX]{x1D70F}$
(panel d), with
$t/\unicode[STIX]{x1D70F}$
(panel d), with
![]() $r_{b}$
the bridge radius,
$r_{b}$
the bridge radius,
![]() $t$
the simulation time and
$t$
the simulation time and
![]() $\unicode[STIX]{x1D70F}$
a characteristic time scale defined as
$\unicode[STIX]{x1D70F}$
a characteristic time scale defined as
![]() $\unicode[STIX]{x1D70F}=\sqrt{R^{3}/\unicode[STIX]{x1D70E}}$
. As evidenced in the figure, the growth of the liquid bridge follows a scaling law
$\unicode[STIX]{x1D70F}=\sqrt{R^{3}/\unicode[STIX]{x1D70E}}$
. As evidenced in the figure, the growth of the liquid bridge follows a scaling law
![]() $r_{b}\propto (t/\unicode[STIX]{x1D70F})^{0.5}$
, with the data collapsing on a single master curve
$r_{b}\propto (t/\unicode[STIX]{x1D70F})^{0.5}$
, with the data collapsing on a single master curve
![]() $r_{b}/R=1.6\sqrt{t/\unicode[STIX]{x1D70F}}$
. It is also worth noting that the prefactor predicted by the simulations (
$r_{b}/R=1.6\sqrt{t/\unicode[STIX]{x1D70F}}$
. It is also worth noting that the prefactor predicted by the simulations (
![]() $1.6$
) is in very close agreement with the value
$1.6$
) is in very close agreement with the value
![]() $1.62$
reported in Duchemin, Eggers & Josserand (Reference Duchemin, Eggers and Josserand2003).
$1.62$
reported in Duchemin, Eggers & Josserand (Reference Duchemin, Eggers and Josserand2003).

Figure 2. (a–c) Bubble formation during the droplet coalescence process due to the fact that only a fraction of the fluid caught in the narrow gap between the two spheres is able to escape. The rest accumulates in a ‘bubble’, that forms at the meniscus (Eggers et al.
Reference Eggers, Lister and Stone1999). (d) Normalized bridge radius as a function of the non-dimensional time
![]() $t/\unicode[STIX]{x1D70F}$
, where
$t/\unicode[STIX]{x1D70F}$
, where
![]() $\unicode[STIX]{x1D70F}=\sqrt{R^{3}/\unicode[STIX]{x1D70E}}$
, for different values of the kinematic viscosity (symbols). In agreement with Eggers et al. (Reference Eggers, Lister and Stone1999), the liquid bridge radius
$\unicode[STIX]{x1D70F}=\sqrt{R^{3}/\unicode[STIX]{x1D70E}}$
, for different values of the kinematic viscosity (symbols). In agreement with Eggers et al. (Reference Eggers, Lister and Stone1999), the liquid bridge radius
![]() $r_{b}$
is shown to follow a scaling law
$r_{b}$
is shown to follow a scaling law
![]() $r_{b}\propto t^{1/2}$
with a dimensionless prefactor of
$r_{b}\propto t^{1/2}$
with a dimensionless prefactor of
![]() $1.6$
, in close agreement with the value
$1.6$
, in close agreement with the value
![]() $1.62$
, reported in Duchemin et al. (Reference Duchemin, Eggers and Josserand2003).
$1.62$
, reported in Duchemin et al. (Reference Duchemin, Eggers and Josserand2003).

Figure 3. Collision sequences for three different impact numbers at different Weber numbers: (a)
![]() $b=0$
and
$b=0$
and
![]() $We=10$
; (b)
$We=10$
; (b)
![]() $b=0.33$
and
$b=0.33$
and
![]() $We=10$
; (c)
$We=10$
; (c)
![]() $b=0.85$
and
$b=0.85$
and
![]() $We=7$
. Upper row experiments (Chen & Chen Reference Chen and Chen2006), lower row simulation results.
$We=7$
. Upper row experiments (Chen & Chen Reference Chen and Chen2006), lower row simulation results.
Table 1. Droplets collision: simulation parameters (lattice units). From the first column on the left: number of computational nodes, droplets diameter, relative impact velocity, surface tension, strength of the near-contact force, kinematic viscosity, impact number, Weber and Reynolds numbers.
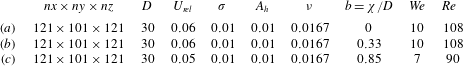
3.2 Bouncing colliding droplets
In this subsection, we show the capability of the extended LB model to accurately reproduce the correct dynamics of head-on and off-axis collisions between two bouncing droplets (Chen & Chen Reference Chen and Chen2006). The characteristic non-dimensional parameters governing the collision outcome are the Weber and the Reynolds numbers, defined as
![]() $We=\unicode[STIX]{x1D70C}U_{rel}^{2}D/\unicode[STIX]{x1D70E}$
and
$We=\unicode[STIX]{x1D70C}U_{rel}^{2}D/\unicode[STIX]{x1D70E}$
and
![]() $Re=U_{rel}D/\unicode[STIX]{x1D708}$
, respectively. In the above,
$Re=U_{rel}D/\unicode[STIX]{x1D708}$
, respectively. In the above,
![]() $U_{rel}$
is the relative impact velocity,
$U_{rel}$
is the relative impact velocity,
![]() $D$
the droplet diameter,
$D$
the droplet diameter,
![]() $\unicode[STIX]{x1D70E}$
the surface tension coefficient and
$\unicode[STIX]{x1D70E}$
the surface tension coefficient and
![]() $\unicode[STIX]{x1D708}$
the kinematic viscosity, as well as the impact number
$\unicode[STIX]{x1D708}$
the kinematic viscosity, as well as the impact number
![]() $b=\unicode[STIX]{x1D712}/D$
, namely, the distance between the collision trajectories in units of the droplet diameter. In table 1, we report the main simulation parameters (expressed in lattice units).
$b=\unicode[STIX]{x1D712}/D$
, namely, the distance between the collision trajectories in units of the droplet diameter. In table 1, we report the main simulation parameters (expressed in lattice units).
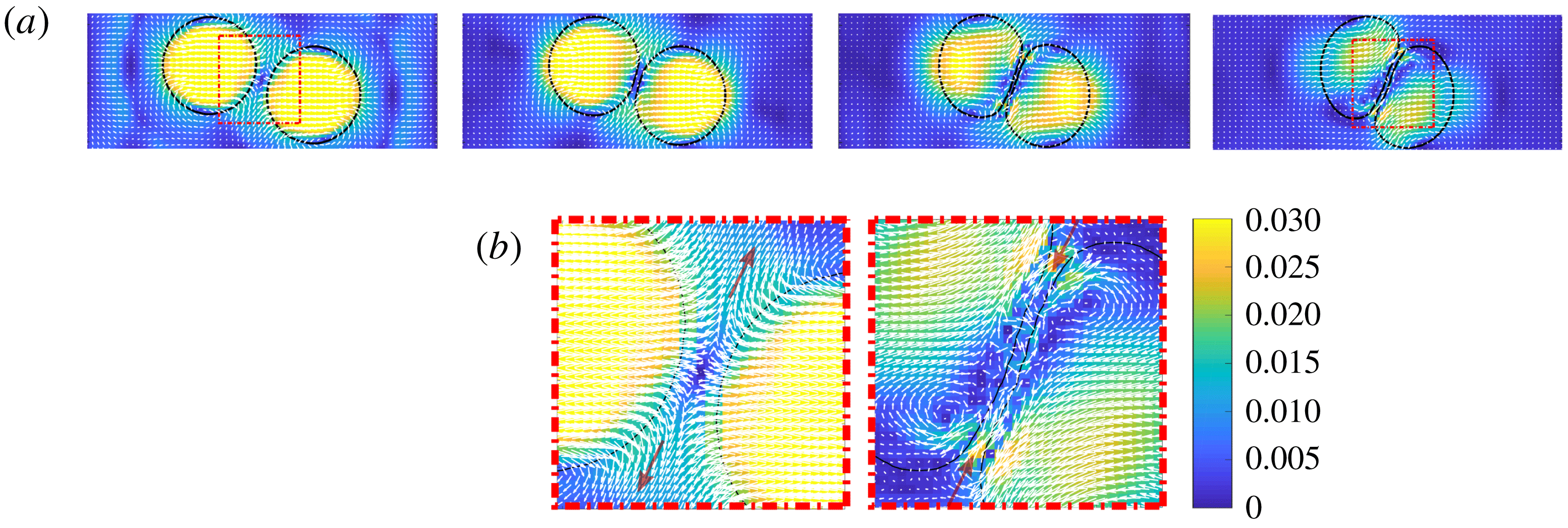
Figure 4. Sequence of the flow field during the impact between the two droplets (mid-plane slice). As shown in (b), during the first stage of the collision the dispersed phase flows outwards, allowing the two droplets to approach. Afterwards, when the droplets come into close contact, the fluid within the thin film begins to recirculate, thereby preventing film rupture hence the coalescence between the droplets. A remark is in order: in real interacting systems the thin film between two interfaces in near contact develops on characteristic length scales of the order of the nanometres, far below the spatial scales accessible to our simulations. Indeed, in (b), the smallest spatial scale is approximately
![]() $20~\unicode[STIX]{x03BC}\text{m}$
while the characteristic distance between two non-coalescing impacting droplets is of the order of one to ten nanometres, i.e. three orders of magnitude smaller than the grid size.
$20~\unicode[STIX]{x03BC}\text{m}$
while the characteristic distance between two non-coalescing impacting droplets is of the order of one to ten nanometres, i.e. three orders of magnitude smaller than the grid size.
Also in this case, the viscosity ratio between the droplets and the surrounding phase has been set to unity. Figure 3 shows three collision sequences for different impact, Weber and Reynolds numbers. The collision outcomes are compared with those reported in Chen & Chen (Reference Chen and Chen2006). The experiments were performed with near-millimetric droplets of immiscible fluids, with diameters ranging between
![]() $700{-}800~\unicode[STIX]{x03BC}\text{m}$
and impact velocities in the range of
$700{-}800~\unicode[STIX]{x03BC}\text{m}$
and impact velocities in the range of
![]() $1{-}3~\text{m}~\text{s}^{-1}$
. The other relevant parameters can be found in Chen & Chen (Reference Chen and Chen2006). By taking a droplet diameter of
$1{-}3~\text{m}~\text{s}^{-1}$
. The other relevant parameters can be found in Chen & Chen (Reference Chen and Chen2006). By taking a droplet diameter of
![]() $700~\unicode[STIX]{x03BC}\text{m}$
, discretized with
$700~\unicode[STIX]{x03BC}\text{m}$
, discretized with
![]() $30$
lattice units, we obtain a lattice spacing
$30$
lattice units, we obtain a lattice spacing
![]() $\unicode[STIX]{x0394}x\approx 20~\unicode[STIX]{x03BC}\text{m}=1~\text{lu}$
, which is the minimum interaction distance between the simulated droplets.
$\unicode[STIX]{x0394}x\approx 20~\unicode[STIX]{x03BC}\text{m}=1~\text{lu}$
, which is the minimum interaction distance between the simulated droplets.
It is worth noting that the thin film between two interfaces in near contact has characteristic length scales of the order of nanometres, far below the spatial scales accessible to our simulations. Indeed, in our simulations, the smallest spatial scale is approximately
![]() $20~\unicode[STIX]{x03BC}\text{m}$
(
$20~\unicode[STIX]{x03BC}\text{m}$
(
![]() $\unicode[STIX]{x0394}x$
), while the characteristic distance between two non-coalescing impacting droplets is of the order of 1–10 nm, i.e. three orders of magnitude smaller than the grid size. Notwithstanding this gap, by matching the main governing parameters (Weber and Reynolds numbers), the overall impact dynamics is correctly captured by the simulations. This, again, calls into question the universality of the underlying physical processes, i.e. at the spatial scale at hand, the interaction physics depends upon the dimensionless numbers, measuring the relative strength of the interactions, rather than on the strength of the interactions themselves. Panel (a) reports the sequence of a head-on collision between two equally sized droplets. As expected, at these Weber and Reynolds numbers, the two droplets bounce off without coalescing, because the coalescence is frustrated by the effect of the near-contact repulsive forces.
$\unicode[STIX]{x0394}x$
), while the characteristic distance between two non-coalescing impacting droplets is of the order of 1–10 nm, i.e. three orders of magnitude smaller than the grid size. Notwithstanding this gap, by matching the main governing parameters (Weber and Reynolds numbers), the overall impact dynamics is correctly captured by the simulations. This, again, calls into question the universality of the underlying physical processes, i.e. at the spatial scale at hand, the interaction physics depends upon the dimensionless numbers, measuring the relative strength of the interactions, rather than on the strength of the interactions themselves. Panel (a) reports the sequence of a head-on collision between two equally sized droplets. As expected, at these Weber and Reynolds numbers, the two droplets bounce off without coalescing, because the coalescence is frustrated by the effect of the near-contact repulsive forces.
The bouncing collision also occurs by increasing the impact parameter (b,c). Indeed, in both cases, the impact velocity is not sufficient to break the intervening thin film and a kissing-like collision is finally observed.
We then inspected the evolution of the thin liquid film during the collision process. As reported in figure 4, in a first stage, the fluid between the two droplets flows outwards, thus allowing the droplets to approach each other (b, left). Afterwards, as they get closer, the liquid begins to recirculate inwards within the intervening film, stabilizing it and preventing the coalescence between the colliding droplets (b, right).
This phenomenon resembles the so-called Marangoni flow in liquid films, namely a fluid recirculation occurring in liquid thin films in the presence of shear and temperature gradients, which was observed to prevent the coalescence between bodies of liquids (Dell’Aversana, Banavar & Koplik Reference Dell’Aversana, Banavar and Koplik1996).
It is straightforward to note that, by varying the magnitude of the repulsive force, it is possible to promote or inhibit the coalescence of the impacting droplets.
From this standpoint, it proves expedient to introduce two further non-dimensional parameters, which measure the relative strength of inertia and surface tension versus repulsive forces. The first, (
![]() $S_{\unicode[STIX]{x1D70E}}$
) is defined as the ratio between the repulsive force (
$S_{\unicode[STIX]{x1D70E}}$
) is defined as the ratio between the repulsive force (
![]() ${\sim}A_{hM}$
) which frustrates the coalescence between droplets, and the surface tension (
${\sim}A_{hM}$
) which frustrates the coalescence between droplets, and the surface tension (
![]() $\unicode[STIX]{x1D70E}$
), which promotes it. The second (
$\unicode[STIX]{x1D70E}$
), which promotes it. The second (
![]() $S_{\unicode[STIX]{x1D705}}$
), is defined as the ratio between the local impact kinetic energy and the work done by the repulsive forces to prevent the two interfaces from coalescing.
$S_{\unicode[STIX]{x1D705}}$
), is defined as the ratio between the local impact kinetic energy and the work done by the repulsive forces to prevent the two interfaces from coalescing.
The two non-dimensional parameters read as follows:
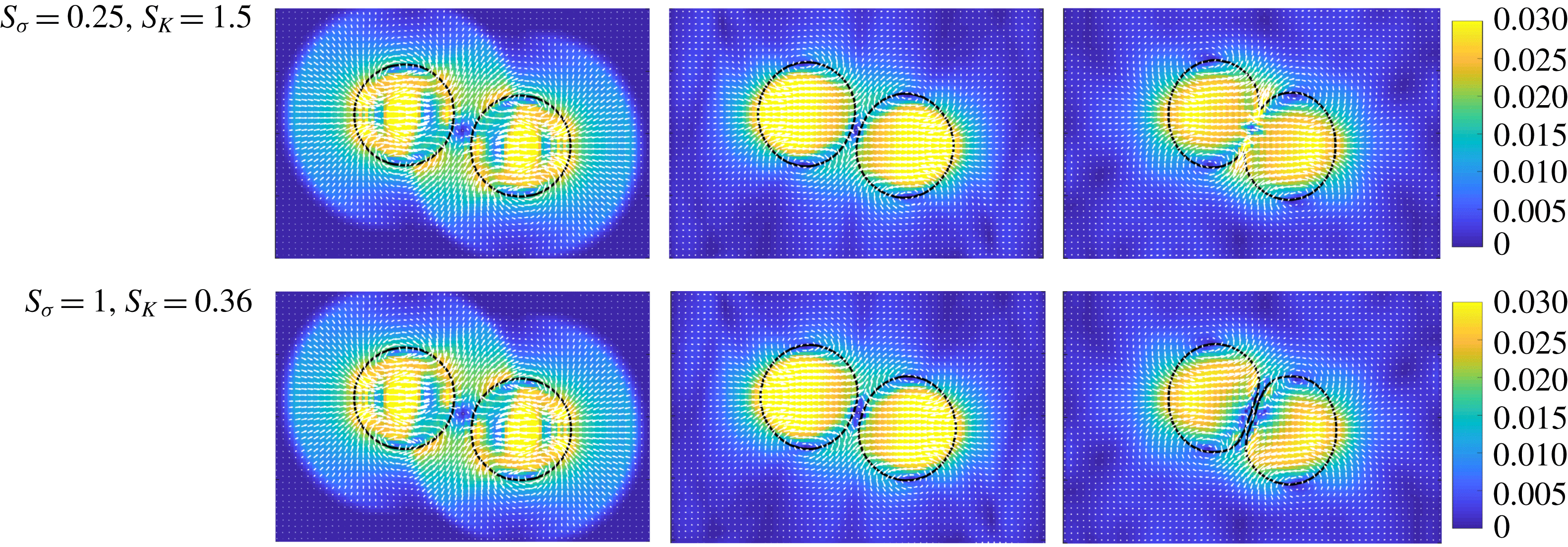
Figure 5. Effect of the magnitude of the near-contact force. The upper panel reports a flow field sequence of two impacting droplets (mid-plane slice). The simulation parameters are the same as those reported in table 1, except for the repulsive parameter, which is four times smaller. It is evident that the repulsive force is not strong enough to frustrate the coalescence between the two impacting droplets, as occurs in the case reported in the lower panel (
![]() $S_{\unicode[STIX]{x1D70E}}=1,S_{\unicode[STIX]{x1D705}}=0.36$
).
$S_{\unicode[STIX]{x1D70E}}=1,S_{\unicode[STIX]{x1D705}}=0.36$
).
In the above
![]() $\unicode[STIX]{x0394}x$
, the lattice spacing, is the characteristic length scale of near-contact interactions between two droplets on the lattice. In our simulations
$\unicode[STIX]{x0394}x$
, the lattice spacing, is the characteristic length scale of near-contact interactions between two droplets on the lattice. In our simulations
![]() $S_{\unicode[STIX]{x1D70E}}=1$
and
$S_{\unicode[STIX]{x1D70E}}=1$
and
![]() $S_{\unicode[STIX]{x1D705}}=0.36$
, meaning that the inertial and the surface forces (both promoting coalescence) are not strong enough to withstand the effect of the local repulsion.
$S_{\unicode[STIX]{x1D705}}=0.36$
, meaning that the inertial and the surface forces (both promoting coalescence) are not strong enough to withstand the effect of the local repulsion.
By lowering the intensity of the repulsive forces by a factor four (
![]() $S_{\unicode[STIX]{x1D705}}=1.5$
and
$S_{\unicode[STIX]{x1D705}}=1.5$
and
![]() $S_{\unicode[STIX]{x1D70E}}=0.25$
), we finally observe the coalescence between the impacting droplets (see figure 5). It will be shown below (§ 3.4) that the balance between inertia, surface forces and repulsive actions crucially affects the formation and the overall dynamics of crystal-like structures in foams and emulsions.
$S_{\unicode[STIX]{x1D70E}}=0.25$
), we finally observe the coalescence between the impacting droplets (see figure 5). It will be shown below (§ 3.4) that the balance between inertia, surface forces and repulsive actions crucially affects the formation and the overall dynamics of crystal-like structures in foams and emulsions.
3.3 Dense emulsion in a planar channel
We now discuss the pressure-driven flow of a dense emulsion within a narrow channel, made of a regular arrangement of equal-sized droplets (component A) dispersed in a continuous matrix (component B) (see figure 6). The simulations are performed on a
![]() $137\times 1\times 137$
(
$137\times 1\times 137$
(
![]() $H\times W\times L$
) node domain. The viscosities of both the dispersed and the continuous phase are set to
$H\times W\times L$
) node domain. The viscosities of both the dispersed and the continuous phase are set to
![]() $0.167$
, while the surface tension is set to
$0.167$
, while the surface tension is set to
![]() $\unicode[STIX]{x1D70E}=0.02$
(both in lattice units). Periodic boundary conditions have been applied to the cross-flow and along the flow direction while, on the upper and lower walls, no-slip conditions have been imposed. The static contact angle between the dispersed phase and the solid walls is set to
$\unicode[STIX]{x1D70E}=0.02$
(both in lattice units). Periodic boundary conditions have been applied to the cross-flow and along the flow direction while, on the upper and lower walls, no-slip conditions have been imposed. The static contact angle between the dispersed phase and the solid walls is set to
![]() $180^{\circ }$
(pure hydrophobic walls). A body force (
$180^{\circ }$
(pure hydrophobic walls). A body force (
![]() $g=10^{-5}$
, in lattice units) is employed to mimic the effect of an applied pressure gradient along the channel. The value of
$g=10^{-5}$
, in lattice units) is employed to mimic the effect of an applied pressure gradient along the channel. The value of
![]() $g$
was chosen so as to keep the Reynolds number sufficiently low (
$g$
was chosen so as to keep the Reynolds number sufficiently low (
![]() $Re\leqslant 10$
) to guarantee laminar flow conditions within the channel, as typical of microfluidic channels.
$Re\leqslant 10$
) to guarantee laminar flow conditions within the channel, as typical of microfluidic channels.
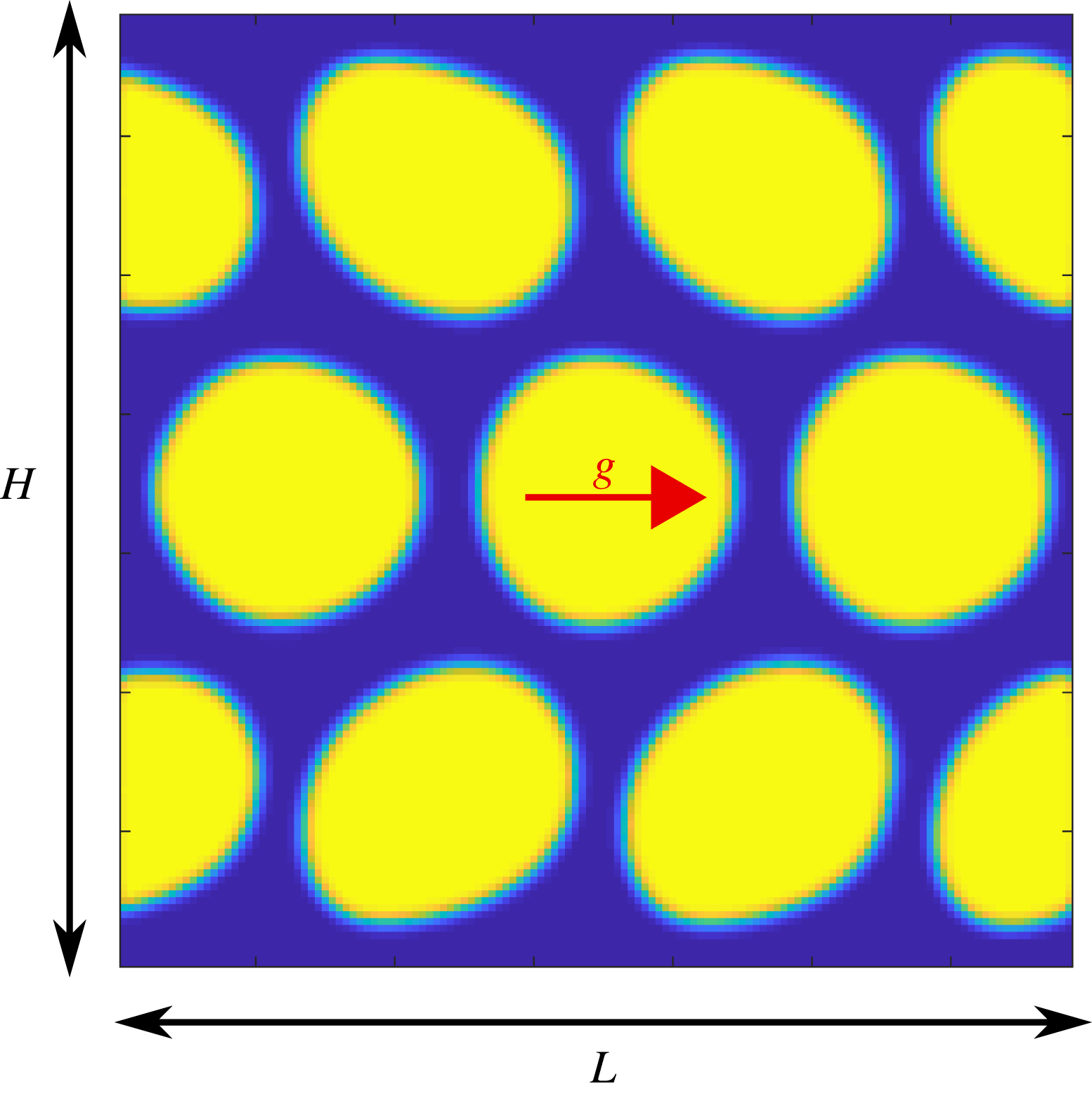
Figure 6. Sketch of the pressure-driven flow of an emulsion in a narrow channel:
![]() $H\times L=137\times 137$
while
$H\times L=137\times 137$
while
![]() $g$
, the applied force employed to mimic the pressure gradient along the channel, is set to
$g$
, the applied force employed to mimic the pressure gradient along the channel, is set to
![]() $10^{-5}$
, to guarantee laminar flow conditions.
$10^{-5}$
, to guarantee laminar flow conditions.
Figure 7(b) reports the averaged velocity profiles at different values of the packing fraction,
![]() $\unicode[STIX]{x1D719}=n\cdot V_{drop}/V_{tot}$
, with
$\unicode[STIX]{x1D719}=n\cdot V_{drop}/V_{tot}$
, with
![]() $n$
the number of droplets in the channel,
$n$
the number of droplets in the channel,
![]() $V_{drop}$
the volume of the (cylindrical) droplet and
$V_{drop}$
the volume of the (cylindrical) droplet and
![]() $V_{tot}$
the volume of the channel. When
$V_{tot}$
the volume of the channel. When
![]() $\unicode[STIX]{x1D719}=0$
, the usual Poiseuille flow parabolic profile for a pure fluid is recovered, as shown in figure 7(a).
$\unicode[STIX]{x1D719}=0$
, the usual Poiseuille flow parabolic profile for a pure fluid is recovered, as shown in figure 7(a).
As
![]() $\unicode[STIX]{x1D719}$
increases, the velocity profiles flatten in the central region of the channel. In order to quantify the effect of the packing fraction, we measured the effective (or relative) dynamic viscosity, defined as the flow rate ratio
$\unicode[STIX]{x1D719}$
increases, the velocity profiles flatten in the central region of the channel. In order to quantify the effect of the packing fraction, we measured the effective (or relative) dynamic viscosity, defined as the flow rate ratio
![]() $\unicode[STIX]{x1D707}_{eff}=Q(\unicode[STIX]{x1D719}=0)/Q(\unicode[STIX]{x1D719})$
and compared it against the model proposed by Taylor (Reference Taylor1932) and Bullard et al. (Reference Bullard, Pauli, Garboczi and Martys2009). In Taylor theory, the effective dynamic viscosity (for
$\unicode[STIX]{x1D707}_{eff}=Q(\unicode[STIX]{x1D719}=0)/Q(\unicode[STIX]{x1D719})$
and compared it against the model proposed by Taylor (Reference Taylor1932) and Bullard et al. (Reference Bullard, Pauli, Garboczi and Martys2009). In Taylor theory, the effective dynamic viscosity (for
![]() $\unicode[STIX]{x1D708}_{d}/\unicode[STIX]{x1D708}_{c}=1$
) can be expressed as a linear function of the volume fraction (in the limit of small droplets and volume fractions) as follows:
$\unicode[STIX]{x1D708}_{d}/\unicode[STIX]{x1D708}_{c}=1$
) can be expressed as a linear function of the volume fraction (in the limit of small droplets and volume fractions) as follows:
The effective dynamic viscosity predicted by Bullard, which is based on the differential effective medium theory, reads as follows:
with
![]() $[\unicode[STIX]{x1D702}]$
the intrinsic viscosity, whose value is restricted between the undeformable and the freely deformable limit (Douglas & Garboczi Reference Douglas and Garboczi1995). As reported in figure 7(a), the simulation results are a very close match with respect to the theoretical prediction of Taylor (inset in figure 7
a) and Bullard (with intrinsic viscosity set to
$[\unicode[STIX]{x1D702}]$
the intrinsic viscosity, whose value is restricted between the undeformable and the freely deformable limit (Douglas & Garboczi Reference Douglas and Garboczi1995). As reported in figure 7(a), the simulation results are a very close match with respect to the theoretical prediction of Taylor (inset in figure 7
a) and Bullard (with intrinsic viscosity set to
![]() $[\unicode[STIX]{x1D702}]=1$
).
$[\unicode[STIX]{x1D702}]=1$
).

Figure 7. (a) Measured
![]() $\unicode[STIX]{x1D707}_{eff}$
(symbols) as a function of droplet volume fraction
$\unicode[STIX]{x1D707}_{eff}$
(symbols) as a function of droplet volume fraction
![]() $\unicode[STIX]{x1D719}$
. The solid line is a fit based on the differential effective medium theory (Bullard et al.
Reference Bullard, Pauli, Garboczi and Martys2009). In the inset, we report also the Taylor theory (
$\unicode[STIX]{x1D719}$
. The solid line is a fit based on the differential effective medium theory (Bullard et al.
Reference Bullard, Pauli, Garboczi and Martys2009). In the inset, we report also the Taylor theory (
![]() $\unicode[STIX]{x1D708}_{d}/\unicode[STIX]{x1D708}_{c}=1$
), (solid line) (
$\unicode[STIX]{x1D708}_{d}/\unicode[STIX]{x1D708}_{c}=1$
), (solid line) (
![]() $1+1.75\unicode[STIX]{x1D719}$
), which holds for small values of the volume fraction, versus the simulations. (b) Averaged velocity profiles as a function of the packing fraction
$1+1.75\unicode[STIX]{x1D719}$
), which holds for small values of the volume fraction, versus the simulations. (b) Averaged velocity profiles as a function of the packing fraction
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
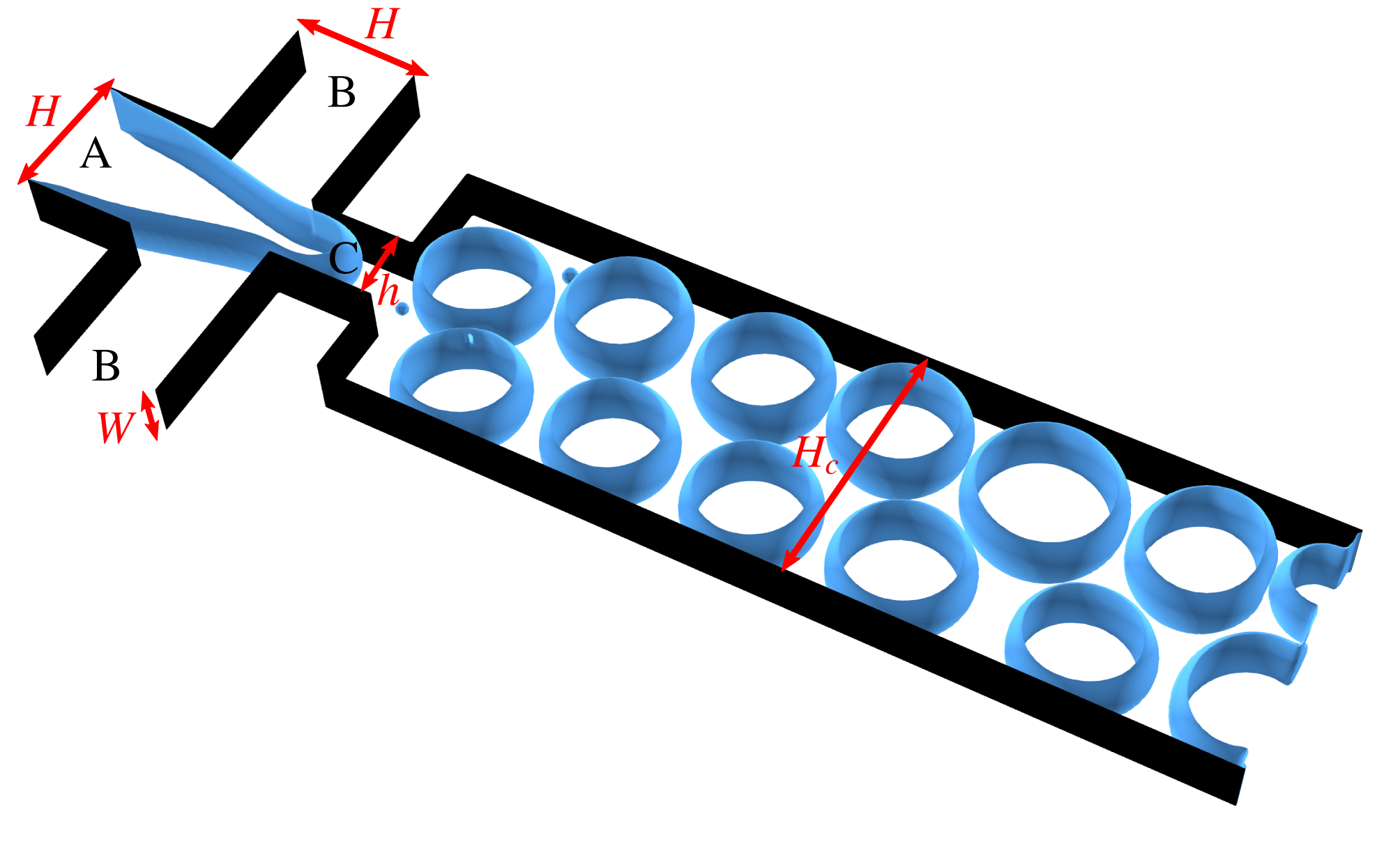
Figure 8. Sketch of the flow focuser device.
3.4 Soft flowing crystals in a microfluidic focuser
As an application, we simulated the formation of oil/water emulsions in a microfluidics flow focusing device, whose sketch is reported in figure 8. The micro-device is made of three channels supplying the dispersed (A) and the continuous (B) phase, plus an orifice (C) placed downstream of the three coaxial inlet streams.
The mechanism of droplet formation follows from the periodic pinch-off of the dispersed jet by the continuous stream and the pinch-off mechanism takes place in the small orifice.
Flow focusers are nowadays widely employed for the production of mono-dispersed emulsions, due to the precise control over the emulsion monodispersity and the droplet size (Whitesides Reference Whitesides2006; Sackmann, Fulton & Beebe Reference Sackmann, Fulton and Beebe2014; Cruz-Mazo et al.
Reference Cruz-Mazo, Herrada, Gañán-Calvo and Montanero2017). The high degree of flow reproducibility is due to the dominance of the viscous forces over inertia which smooths flows and tames hydrodynamic instabilities. The pinch-off process is thus metronomic, allowing to produce droplets with measured standard deviations in size as little as
![]() $0.1\,\%$
(Ganán-Calvo & Gordillo Reference Ganán-Calvo and Gordillo2001; Link et al.
Reference Link, Anna, Weitz and Stone2004; Marmottant & Raven Reference Marmottant and Raven2009).
$0.1\,\%$
(Ganán-Calvo & Gordillo Reference Ganán-Calvo and Gordillo2001; Link et al.
Reference Link, Anna, Weitz and Stone2004; Marmottant & Raven Reference Marmottant and Raven2009).
Table 2. Flow focuser simulations: main parameters (lattice units). From the first column on the left: number of computational nodes, device characteristics, inlet velocity of the dispersed phase, inlet velocity of the continuous phase, dispersed phase viscosity, continuous phase viscosity, repulsive interaction parameter, flow rate ratio. The viscosity ratio between the droplets and the surrounding phase has been set to
![]() $\unicode[STIX]{x1D708}_{d}/\unicode[STIX]{x1D708}_{c}=1/7$
.
$\unicode[STIX]{x1D708}_{d}/\unicode[STIX]{x1D708}_{c}=1/7$
.

Here, we show that the mesoscale approach proposed in this paper is able to reproduce different packing configurations in the outlet channel of the flow focuser, which are obtained by varying the dispersed-to-continuous flow rate ratio. Moreover, we also show that, by tuning the magnitude of the near-contact force interaction, different structures of the flowing crystals can be achieved. The simulation setup is sketched in figure 8, while the main simulation parameters are reported in table 2.
The prototypical focuser, used in the simulations, consists of three main channels (A and B) of width
![]() $H=200~\unicode[STIX]{x03BC}\text{m}$
, a nozzle (C)
$H=200~\unicode[STIX]{x03BC}\text{m}$
, a nozzle (C)
![]() $h=100~\unicode[STIX]{x03BC}\text{m}$
and an outlet channel of width
$h=100~\unicode[STIX]{x03BC}\text{m}$
and an outlet channel of width
![]() $H_{c}=400~\unicode[STIX]{x03BC}\text{m}$
, while the height of the focuser is
$H_{c}=400~\unicode[STIX]{x03BC}\text{m}$
, while the height of the focuser is
![]() $W=100~\unicode[STIX]{x03BC}\text{m}$
. By taking an interfacial tension of an oil–water mixture (
$W=100~\unicode[STIX]{x03BC}\text{m}$
. By taking an interfacial tension of an oil–water mixture (
![]() ${\sim}50~\text{mN}~\text{m}^{-1}$
), the dynamic viscosity of the water (dispersed phase)
${\sim}50~\text{mN}~\text{m}^{-1}$
), the dynamic viscosity of the water (dispersed phase)
![]() $\unicode[STIX]{x1D707}\sim 10^{-3}~~\text{Pa}~\text{s}$
and an inlet velocity of the dispersed phase
$\unicode[STIX]{x1D707}\sim 10^{-3}~~\text{Pa}~\text{s}$
and an inlet velocity of the dispersed phase
![]() ${\sim}0.1~\text{m}~\text{s}^{-1}$
we obtain a Weber number
${\sim}0.1~\text{m}~\text{s}^{-1}$
we obtain a Weber number
![]() $We=0.04$
and a capillary number
$We=0.04$
and a capillary number
![]() $Ca=0.0017$
, which are typical of flow focuser devices (Marmottant & Raven Reference Marmottant and Raven2009). Figure 9 reports two different flow configurations which can be obtained by varying the flow rate ratios between the dispersed and the continuous phase. In both cases, droplets readily self-assemble in ordered patterns described as soft flowing crystals (Garstecki & Whitesides Reference Garstecki and Whitesides2006; Marmottant & Raven Reference Marmottant and Raven2009; Dollet, Scagliarini & Sbragaglia Reference Dollet, Scagliarini and Sbragaglia2015). In (a) (
$Ca=0.0017$
, which are typical of flow focuser devices (Marmottant & Raven Reference Marmottant and Raven2009). Figure 9 reports two different flow configurations which can be obtained by varying the flow rate ratios between the dispersed and the continuous phase. In both cases, droplets readily self-assemble in ordered patterns described as soft flowing crystals (Garstecki & Whitesides Reference Garstecki and Whitesides2006; Marmottant & Raven Reference Marmottant and Raven2009; Dollet, Scagliarini & Sbragaglia Reference Dollet, Scagliarini and Sbragaglia2015). In (a) (
![]() $\unicode[STIX]{x1D719}=1/2$
), the reported sequence shows a typical wet foam-like configuration in which the droplets are circular (cylinders in three dimensions) and automatically arrange on three rows, as evidenced in figure 9(c), which also provides a visual comparison with the experimental data reported in Marmottant & Raven (Reference Marmottant and Raven2009). Panel (b) (
$\unicode[STIX]{x1D719}=1/2$
), the reported sequence shows a typical wet foam-like configuration in which the droplets are circular (cylinders in three dimensions) and automatically arrange on three rows, as evidenced in figure 9(c), which also provides a visual comparison with the experimental data reported in Marmottant & Raven (Reference Marmottant and Raven2009). Panel (b) (
![]() $\unicode[STIX]{x1D719}=1/1$
) shows a more ordered crystal structure, made of larger cylindrical droplets disposed along two staggered rows. We further investigated the effect of the magnitude of the near force on the formation of the crystal pattern. Figure 10(a) shows a time sequence of the flow field during the break-up stage occurring downstream of the striction of the focuser, with a magnitude of the near-contact force lowered by a factor
$\unicode[STIX]{x1D719}=1/1$
) shows a more ordered crystal structure, made of larger cylindrical droplets disposed along two staggered rows. We further investigated the effect of the magnitude of the near force on the formation of the crystal pattern. Figure 10(a) shows a time sequence of the flow field during the break-up stage occurring downstream of the striction of the focuser, with a magnitude of the near-contact force lowered by a factor
![]() $5$
with respect to the base case of figure 9(b). It is evident that the magnitude of the repulsive force is no longer sufficient to prevent the coalescence between the droplet downstream the striction and the upstream jet, due to the high impact velocity. Thus, as evidenced in panel (c), the droplets in the outlet channel are approximately twice the size with respect to the previous case, and proceed in single-file motion, i.e. aligned along the horizontal axes of the focuser. It is also interesting to note that the action of the repulsive force keeps frustrating the coalescence in the outlet channel, where the typical velocities are much lower than at the exit of the nozzle. Once again, we can compute the non-dimensional parameter
$5$
with respect to the base case of figure 9(b). It is evident that the magnitude of the repulsive force is no longer sufficient to prevent the coalescence between the droplet downstream the striction and the upstream jet, due to the high impact velocity. Thus, as evidenced in panel (c), the droplets in the outlet channel are approximately twice the size with respect to the previous case, and proceed in single-file motion, i.e. aligned along the horizontal axes of the focuser. It is also interesting to note that the action of the repulsive force keeps frustrating the coalescence in the outlet channel, where the typical velocities are much lower than at the exit of the nozzle. Once again, we can compute the non-dimensional parameter
![]() $S_{\unicode[STIX]{x1D705}}$
, downstream of the nozzle, where the coalescence occurs. By taking a characteristic jet velocity
$S_{\unicode[STIX]{x1D705}}$
, downstream of the nozzle, where the coalescence occurs. By taking a characteristic jet velocity
![]() $U_{J}\sim 0.1$
, we estimate
$U_{J}\sim 0.1$
, we estimate
![]() $S_{\unicode[STIX]{x1D705}}\sim 1.4$
(figure 10
a) and
$S_{\unicode[STIX]{x1D705}}\sim 1.4$
(figure 10
a) and
![]() $S_{\unicode[STIX]{x1D705}}\sim 0.18$
(figure 10
b). Thus,
$S_{\unicode[STIX]{x1D705}}\sim 0.18$
(figure 10
b). Thus,
![]() $S_{\unicode[STIX]{x1D705}}\sim O(1)$
may be interpreted as a threshold above which the repulsive force is no longer able to balance the inertia, so as to frustrate the coalescence between the jet and the droplet. These preliminary simulations clearly highlight the pivotal role of the near-contact interactions on the structure of the resulting flowing crystal.
$S_{\unicode[STIX]{x1D705}}\sim O(1)$
may be interpreted as a threshold above which the repulsive force is no longer able to balance the inertia, so as to frustrate the coalescence between the jet and the droplet. These preliminary simulations clearly highlight the pivotal role of the near-contact interactions on the structure of the resulting flowing crystal.

Figure 9. (a,b) Different configurations of monodispersed emulsions at the outlet of the flow focuser, on an
![]() $xy$
midplane, obtained by changing the dispersed/continuous flowrate ratios. (c) Zoom of the three droplets foam structure: visual comparison between experiments ((Marmottant & Raven Reference Marmottant and Raven2009), left panel) and numerical simulations (right panel).
$xy$
midplane, obtained by changing the dispersed/continuous flowrate ratios. (c) Zoom of the three droplets foam structure: visual comparison between experiments ((Marmottant & Raven Reference Marmottant and Raven2009), left panel) and numerical simulations (right panel).

Figure 10. (a–b) Flow field sequence during the break-up stage occurring at the outlet of the striction of the flow focuser. (a) Lower and (b) higher near-contact forces. In the first case the strength of the repulsive force is not sufficient to prevent the coalescence between the droplet and the jet, due to the high speed of the jet at the outlet of the nozzle. Nonetheless, the repulsive force is strong enough to prevent the coalescence between droplets moving in the outlet channel (c, left figure). In the second case, the repulsive force is strong enough to completely suppress the coalescence between the jet and the newly formed droplets, thus allowing the formation of an ordered soft flowing crystal in the outlet channel.
From this standpoint, the proposed approach may open up new chances to investigate the complex dynamics of flowing microfluidics crystals, helping in identifying the optimal operational regimes required to precisely control the production of mono-dispersed emulsions.
4 Conclusions
The dynamic interactions occurring at fluid interfaces at nanometric and subnanometric scales, are known to play a crucial role on the macroscopic behaviour of complex states of densely packed soft flowing matter, such as colloidal systems, foams and emulsions. As a result, an in-depth knowledge of these dynamic interactions is pivotal to a deeper understanding of the properties of soft flowing crystals (Garstecki & Whitesides Reference Garstecki and Whitesides2006; Marmottant & Raven Reference Marmottant and Raven2009; Montessori et al. Reference Montessori, Lauricella and Succi2019). Many theoretical and experimental researchers have endeavoured to explain the basic physics behind near-contact interactions. Notwithstanding the surge of experimental and theoretical activity, the numerical description of soft flowing matter is still in its early stage.
One reason is that the concurrent solution of the macroscopic equations, needed to evolve the fluid interface, together with a direct description of the near-contact interactions at the nano-scales stands out as a prohibitive multiscale problem.
In this paper, we have proposed a coarse-grained approach to include the effect of the near-contact interactions within the LB computational framework, and shown that such an extended LB model is able to accurately describe a number of relevant physical effects. That is, (i) to capture the evolution of two bouncing impacting droplets for different values of the main governing parameters namely, the Weber, Reynolds and impact numbers; (ii) to predict the effective viscosity of a dense emulsion flowing in a micro-channel, in agreement with the theoretical model of Bullard (Bullard et al. Reference Bullard, Pauli, Garboczi and Martys2009). Moreover, the extended LB approach is also able to reproduce different droplets arrangements at the outlet channel of a microfluidic focuser, thus permitting us to simulate soft flowing crystals at the scale of the actual microfluidic device.
To this purpose, two additional non-dimensional parameters (
![]() $S_{\unicode[STIX]{x1D70E}}$
and
$S_{\unicode[STIX]{x1D70E}}$
and
![]() $S_{\unicode[STIX]{x1D705}}$
) have been introduced which measure the strength of inertia and surface tension versus the repulsive near-contact interactions. We found that
$S_{\unicode[STIX]{x1D705}}$
) have been introduced which measure the strength of inertia and surface tension versus the repulsive near-contact interactions. We found that
![]() $S_{\unicode[STIX]{x1D705}}=1$
acts as a natural threshold, above which the repulsive near-contact forces are no longer able to withstand the impact kinetic energy and prevent the coalescence between colliding fluid interfaces.
$S_{\unicode[STIX]{x1D705}}=1$
acts as a natural threshold, above which the repulsive near-contact forces are no longer able to withstand the impact kinetic energy and prevent the coalescence between colliding fluid interfaces.
Even though in this paper we have discussed the specific case of a flow focuser microfluidic device, the method presented in this work is expected to apply to a much broader variety of engineering and biomedical problems.
An application where our methods can be specifically useful (and in future will be developed for) is the design of systems where droplets would undergo an internal transition from viscous solutions to elastic materials. This in-droplet gelation ‘freezes’ the shape of the microparticles as it is at the outlet channel. The resulting microparticle systems (also produced in microfluidic devices) are employed e.g. for the encapsulation of living cells in hydrogels (biological reactors or sensors for toxicological screening) or of pharmaceutically active compounds in polymer matrices (controlled drug release). By applying our methods to such materials, it will be possible to rationally design complex, micro particle-based flowing crystals, where morphology/aspect ratio and any ensuing properties are precisely and topologically controlled. This would allow e.g. (i) a permanent and tailored modulation of optical properties orthogonally to the channel direction, producing soft waveguides, or (ii) a very fine control of the conditions of dynamic arrest (macroscopic ‘gelation’) of the emulsion or foam obtained through the microfluidic device, which can be particularly useful in applications of 3-D printing.
We would like to stress that the possibility of employing a mesoscale instead of a full-scale description crucially relies upon the universality of the underlying physics or, in other words, its dependence on suitable dimensionless parameters measuring the relative strength of the interactions, rather than on the microscopic details of the interactions themselves. The aim of this work was precisely to present a coarse-grained approach encompassing the basic physical features of near-contact interactions. In this regard, the proposed model represents an up-scale of the interactions occurring at the interface level. Whilst being a dramatic simplification of the underlying physics at the molecular level, the results obtained in this paper suggest that, at least at the spatial scale at hand, a coarse-grained description is appropriate to describe the mesoscale evolution of an interacting multidroplet system. To conclude, it is hoped that the numerical approach presented here may open the way to an experimental-scale modelling of soft flowing crystals, promising new chances to decode the complexity which characterizes this fascinating state of flowing matter.
Acknowledgement
The research leading to these results has received funding from the European Research Council under the European Union’s Horizon 2020 Framework Programme (no. FP/2014- 2020)/ERC grant agreement no. 739964 (COPMAT).














