Article contents
Experiments on flows in channels with spatially distributed heating
Published online by Cambridge University Press: 07 June 2019
Abstract
Flows in channels exposed to spatially distributed heating were investigated. Such flows are of interest as theoretical analyses suggest that heating leads to the reduction of pressure losses. A special apparatus providing the means for the creation of well-controlled spatially periodic heating with the desired intensity as well as precise control of the flow rate in flows with small Reynolds numbers was constructed. The apparatus works with air and provides optical access to the flow interior. The relevant theory has been generalized to handle the temperature fields measured in the experiments. The experiments were carried out for Reynolds numbers 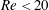 $Re<20$ and at a single Rayleigh number based on the peak-to-peak temperature difference and channel half-height of
$Re<20$ and at a single Rayleigh number based on the peak-to-peak temperature difference and channel half-height of 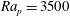 $Ra_{p}=3500$. Flow visualization and particle image velocimetry measurements demonstrated the formation of two-dimensional steady rolls whose size was dictated by
$Ra_{p}=3500$. Flow visualization and particle image velocimetry measurements demonstrated the formation of two-dimensional steady rolls whose size was dictated by 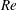 $Re$, with the largest rolls observed for the smallest
$Re$, with the largest rolls observed for the smallest 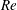 $Re$ and the roll size being gradually reduced as
$Re$ and the roll size being gradually reduced as 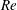 $Re$ increased until their complete elimination at the largest
$Re$ increased until their complete elimination at the largest 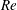 $Re$ used in the experiment. An excellent agreement between the theoretically and experimentally determined complex flow fields was found. Wall shear stresses extracted from the velocity measurements agree with their theoretical counterparts within the expected accuracy. The agreement between the experimental and theoretical velocity fields and their unique relation with the corresponding pressure fields indirectly verify the heating-induced pressure-gradient-reducing effect.
$Re$ used in the experiment. An excellent agreement between the theoretically and experimentally determined complex flow fields was found. Wall shear stresses extracted from the velocity measurements agree with their theoretical counterparts within the expected accuracy. The agreement between the experimental and theoretical velocity fields and their unique relation with the corresponding pressure fields indirectly verify the heating-induced pressure-gradient-reducing effect.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 17
- Cited by


