Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-08T04:28:52.436Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear behaviour of the Mack mode in a hypersonic boundary layer

Published online by Cambridge University Press:  07 June 2019

Stuart A. Craig Open the ORCID record for Stuart A. Craig [Opens in a new window] ,
Raymond A. Humble ,
Jerrod W. Hofferth  and
William S. Saric
Stuart A. Craig*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Arizona, Tucson, AZ 85721, USA
Raymond A. Humble
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843, USA
Jerrod W. Hofferth
Affiliation:
Aerospace Systems Directorate, Air Force Research Laboratory, Arnold AFB, TN 37389, USA
William S. Saric
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

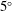Mack-mode waves are measured in a hypersonic boundary layer using high-frequency focusing schlieren deflectometry. Experiments are performed using a $5^{\circ }$ flared cone at 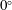$0^{\circ }$ angle of attack in the low-disturbance Mach 6 Quiet Tunnel at Texas A&M University across a free-stream unit Reynolds number range of 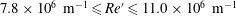$7.8\times 10^{6}~\text{m}^{-1}\leqslant \mathit{Re}^{\prime }\leqslant 11.0\times 10^{6}~\text{m}^{-1}$. The high-frequency response of the measurement system allows harmonics and other nonlinear behaviour to be measured. Mack-mode waves and several harmonics are clearly observed at a frequency of 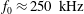$f_{0}\approx 250~\text{kHz}$. Bispectral analysis is used to show that these waves undergo several quadratic phase-coupled sum and difference interactions with themselves to produce harmonics, as well interact with a relatively low-frequency wave that results in amplitude modulation. Bispectral analysis is used to highlight these interactions.

JFM classification

Boundary Layers: Boundary layer stability Aerodynamics: High-speed flow Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 74 - 99
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blanchard, A. E., Lachowicz, J. T. & Wilkinson, S. P. 1997 NASA Langley Mach 6 quiet wind-tunnel performance. AIAA J. 35 (1), 23–28.Google Scholar
Blanchard, A. E. & Selby, G. V.1996 An experimental investigation of wall-cooling effects on hypersonic boundary-layer stability in a quiet wind tunnel. Tech. Rep. NASA CR 198287.Google Scholar
Boedeker, L. R.1959 Analysis and construction of a sharp focussing schlieren system. MS thesis, Massachusetts Institute of Technology, Cambridge, MA.Google Scholar
Bountin, D. A., Shiplyuk, A. N. & Maslov, A. A. 2008 Evolution of nonlinear processes in a hypersonic boundary layer on a sharp cone. J. Fluid Mech. 611, 427–442.Google Scholar
Chen, F.-J., Wilkinson, S. P. & Beckwith, I. E. 1993 Görtler instability and hypersonic quiet nozzle design. J. Spacecr. Rockets 30 (2), 170–175.Google Scholar
Chen, X., Zhu, Y. & Lee, C. 2017 Interactions between second mode and low-frequency waves in a hypersonic boundary layer. J. Fluid Mech. 820, 693–735.Google Scholar
Chokani, N. 1999 Nonlinear spectral dynamics of hypersonic laminar boundary layer flow. Phys. Fluids 11 (12), 3846–3851.Google Scholar
Chokani, N. 2005 Nonlinear evolution of Mack modes in a hypersonic boundary layer. Phys. Fluids 17 (1), 014102.Google Scholar
Collis, W. B., White, P. R. & Hammond, J. K. 1998 Higher-order spectra: the bispectrum and trispectrum. Mech. Syst. Signal Process. 12 (3), 375–394.Google Scholar
Craik, A. D. D. 1971 Non-linear resonant instability in boundary layers. J. Fluid Mech. 50 (02), 393–413.Google Scholar
Doggett, G. P., Chokani, N. & Wilkinson, S. P. 1997 Hypersonic boundary-layer stability experiments on a flared-cone model at angle of attack in a quiet wind tunnel. In 35th Aerospace Sciences Meeting and Exhibit, AIAA 97-0557. AIAA.Google Scholar
Fedorov, A. V. 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–95.Google Scholar
Hader, C. & Fasel, H. F. 2018 Towards simulating natural transition in hypersonic boundary layers via random inflow disturbances. J. Fluid Mech. 847, R3.Google Scholar
Hofferth, J. W., Bowersox, R. D. W. & Saric, W. S. 2010 The Mach 6 quiet tunnel at Texas A&M: quiet flow performance. In 27th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, AIAA 2010-4794. AIAA.Google Scholar
Hofferth, J. W., Humble, R. A., Floryan, D. C. & Saric, W. S. 2013 High-bandwidth optical measurements of the second-mode instability in a Mach 6 quiet tunnel. In 51st AIAA Aerospace Sciences Meeting, AIAA 2013-0378. AIAA.Google Scholar
Hofferth, J. W. & Saric, W. S. 2012 Boundary-layer transition on a flared cone in the Texas A&M Mach 6 quiet tunnel. In 50th AIAA Aerospace Sciences Meeting, AIAA 2012-0923. AIAA.Google Scholar
Horvath, T. J., Berry, S. A., Hollis, B. R., Chang, C.-L. & Singer, B. A. 2002 Boundary layer transition on slender cones in cnventional and low disturbance Mach 6 wind tunnels. In 32nd AIAA Fluid Dynamics Conference and Exhibit, AIAA 2002-2743. AIAA.Google Scholar
Keyes, F. G. 1951 A summary of viscosity and heat-conduction data for He, Ar, H2 , O2 , N2 , CO, CO2 , H2O, and Air. Trans. ASME 73, 589–596.Google Scholar
Kim, Y. C. & Powers, E. J. 1979 Digital bispectral analysis and its applications to nonlinear wave interactions. IEEE Trans. Plasma Sci. 7 (2), 120–131.Google Scholar
Kimmel, R. L. & Kendall, J. M. 1991 Nonlinear disturbances in a hypersonic laminar boundary layer. In 29th Aerospace Sciences Meeting, AIAA 91-0320. AIAA.Google Scholar
Kuehl, J. J. 2018 Thermoacoustic interpretation of second-mode instability. AIAA J. 56 (9), 3585–3592.Google Scholar
Lachowicz, J. T., Chokani, N. & Wilkinson, S. P. 1996 Boundary-layer stability measurements in a hypersonic quiet tunnel. AIAA J. 34 (12), 2496–2500.Google Scholar
Mack, L. M.1969 Boundary-layer stability theory. Tech. Rep., Jet Propulsion Laboratory, Doc. No. 900-277, Rev. A., Pasadena, CA.Google Scholar
Mack, L. M.1984 Boundary-layer linear stability theory. AGARD Rep. No. 709.Google Scholar
Settles, G. S. 2001 Schlieren and Shadowgraph Techniques. Springer.Google Scholar
Settles, G. S. & Hargather, M. J. 2017 A review of recent developments in schlieren and shadowgraph techniques. Meas. Sci. Technol. 28 (4), 042001.Google Scholar
Sivasubramanian, J. & Fasel, H. F. 2014 Numerical investigation of the development of three-dimensional wavepackets in a sharp cone boundary layer at Mach 6. J. Fluid Mech. 756, 600–649.Google Scholar
Sivasubramanian, J. & Fasel, H. F. 2015 Direct numerical simulation of transition in a sharp cone boundary layer at Mach 6: fundamental breakdown. J. Fluid Mech. 768, 175–218.Google Scholar
Stetson, K. F. 1988 On nonlinear aspects of hypersonic boundary-layer stability. AIAA J. 26 (7), 883–885.Google Scholar
Ward, C. A. C., Wheaton, B. M., Chou, A., Berridge, D. C., Letterman, L. E., Luersen, R. P. K. & Schneider, S. P. 2012 Hypersonic boundary-layer transition experiments in the Boeing/AFOSR Mach-6 quiet tunnel. In 50th AIAA Aerospace Sciences Meeting, AIAA 2012-0282. AIAA.Google Scholar
Weinstein, L. M. 1993 Large-field high-brightness focusing schlieren system. AIAA J. 31 (7), 1250–1255.Google Scholar
Welch, P. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15 (2), 70–73.Google Scholar