Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-08T04:33:53.951Z Has data issue: false hasContentIssue false
  • English
  • Français

Velocity and spatial distribution of inertial particles in a turbulent channel flow

Published online by Cambridge University Press:  10 June 2019

Kee Onn Fong Open the ORCID record for Kee Onn Fong [Opens in a new window] ,
Omid Amili  and
Filippo Coletti
Kee Onn Fong*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA St Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
Omid Amili
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Filippo Coletti
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA St Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present experimental observations of the velocity and spatial distribution of inertial particles dispersed in turbulent downward flow through a vertical channel at friction Reynolds numbers 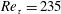$\mathit{Re}_{\unicode[STIX]{x1D70F}}=235$ and 335. The working fluid is air laden with size-selected glass microspheres, having Stokes numbers 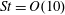$St=\mathit{O}(10)$ and 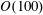$\mathit{O}(100)$ when based on the Kolmogorov and viscous time scales, respectively. Cases at solid volume fractions 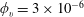$\unicode[STIX]{x1D719}_{v}=3\times 10^{-6}$ and 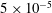$5\times 10^{-5}$ are considered. In the more dilute regime, the particle concentration profile shows near-wall and centreline maxima compatible with a turbophoretic drift down the gradient of turbulence intensity; the particles travel at speed similar to that of the unladen flow except in the near-wall region; and their velocity fluctuations generally follow the unladen flow level over the channel core, exceeding it in the near-wall region. The denser regime presents substantial differences in all measured statistics: the near-wall concentration peak is much more pronounced, while the centreline maximum is absent; the mean particle velocity decreases over the logarithmic and buffer layers; and particle velocity fluctuations and deposition velocities are enhanced. An analysis of the spatial distributions of particle positions and velocities reveals different behaviours in the core and near-wall regions. In the channel core, dense clusters form which are somewhat elongated, tend to be preferentially aligned with the vertical/streamwise direction and travel faster than the less concentrated particles. In the near-wall region, the particles arrange in highly elongated streaks associated with negative streamwise velocity fluctuations, several channel heights in length and spaced by 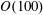$\mathit{O}(100)$ wall units, supporting the view that these are coupled to fluid low-speed streaks typical of wall turbulence. The particle velocity fields contain a significant component of random uncorrelated motion, more prominent for higher 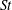$St$ and in the near-wall region.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 367 - 406
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.Google Scholar
Baek, S. J. & Lee, S. J. 1996 A new two-frame particle tracking algorithm using match probability. Exp. Fluids 22 (1), 23–32.Google Scholar
Baker, L., Frankel, A., Mani, A. & Coletti, F. 2017 Coherent clusters of inertial particles in homogeneous turbulence. J. Fluid Mech. 833, 364–398.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Balachandar, S., Liu, K. & Lakhote, M. 2019 Self-induced velocity correction for improved drag estimation in Euler–Lagrange point-particle simulations. J. Comput. Phys. 376, 160–185.Google Scholar
Bendat, J. S. & Piersol, A. G. 2011 Random Data: Analysis and Measurement Procedures, vol. 729. Wiley.Google Scholar
Benson, M., Tanaka, T. & Eaton, J. K. 2005 Effects of wall roughness on particle velocities in a turbulent channel flow. J. Fluids Engng 127 (2), 250–256.Google Scholar
Bernardini, M. 2014 Reynolds number scaling of inertial particle statistics in turbulent channel flows. J. Fluid Mech. 758, R1.Google Scholar
Bewley, G. P., Saw, E.-W. & Bodenschatz, E. 2013 Observation of the sling effect. New J. Phys. 15 (8), 083051.Google Scholar
Bosse, T., Kleiser, L. & Meiburg, E. 2006 Small particles in homogeneous turbulence: settling velocity enhancement by two-way coupling. Phys. Fluids 18 (2), 027102.Google Scholar
Bragg, A. D. & Collins, L. R. 2014 New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distribution of particles. New J. Phys. 16 (5), 055013.Google Scholar
Capecelatro, J. & Desjardins, O. 2013 An Euler–Lagrange strategy for simulating particle–laden flows. J. Comput. Phys. 238, 1–31.Google Scholar
Capecelatro, J. & Desjardins, O. 2015 Mass loading effects on turbulence modulation by particle clustering in dilute and moderately dilute channel flows. J. Fluids Engng 137 (11), 111102.Google Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2016 Strongly coupled fluid–particle flows in vertical channels. I. Reynolds-averaged two-phase turbulence statistics. Phys. Fluids 28 (3), 033306.Google Scholar
Capecelatro, J., Desjardins, O. & Fox, R. O. 2018 On the transition between turbulence regimes in particle–laden channel flows. J. Fluid Mech. 845, 499–519.Google Scholar
Capecelatro, J., Pepiot, P. & Desjardins, O. 2014 Numerical characterization and modeling of particle clustering in wall-bounded vertical risers. Chem. Engng J. 245, 295–310.Google Scholar
Capone, A., Romano, G. P. & Soldati, A. 2015 Experimental investigation on interactions among fluid and rod-like particles in a turbulent pipe jet by means of particle image velocimetry. Exp. Fluids 56 (1), 1.Google Scholar
Caporaloni, M., Tampieri, F., Trombetti, F. & Vittori, O. 1975 Transfer of particles in nonisotropic air turbulence. J. Atmos. Sci. 32 (3), 565–568.Google Scholar
Caraman, N., Borée, J. & Simonin, O. 2003 Effect of collisions on the dispersed phase fluctuation in a dilute tube flow: experimental and theoretical analysis. Phys. Fluids 15 (12), 3602–3612.Google Scholar
Clauser, F. H. 1956 The turbulent boundary layer. Adv. Appl. Mech. 4, 1–51.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 2005 Bubbles, Drops, and Particles. Courier Corporation.Google Scholar
Discetti, S. & Coletti, F. 2018 Volumetric velocimetry for fluid flows. Meas. Sci. Technol. 29 (4), 042001.Google Scholar
Dritselis, C. D. & Vlachos, N. S. 2011 Numerical investigation of momentum exchange between particles and coherent structures in low re turbulent channel flow. Phys. Fluids 23 (2), 025103.Google Scholar
Eaton, J. K. 2009 Two-way coupled turbulence simulations of gas–particle flows using point-particle tracking. Intl J. Multiphase Flow 35 (9), 792–800.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Elghobashi, S. 1994 On predicting particle–laden turbulent flows. Appl. Sci. Res. 52 (4), 309–329.Google Scholar
Ferenc, J.-S. & Néda, Z. 2007 On the size distribution of Poisson Voronoi cells. Physica A 385 (2), 518–526.Google Scholar
Fessler, J. R., Kulick, J. D. & Eaton, J. K. 1994 Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 6 (11), 3742–3749.Google Scholar
Fevrier, P., Simonin, O. & Squires, K. D. 2005 Partitioning of particle velocities in gas–solid turbulent flows into a continuous field and a spatially uncorrelated random distribution: theoretical formalism and numerical study. J. Fluid Mech. 533, 1–46.Google Scholar
Fouxon, I., Schmidt, L., Ditlevsen, P., van Reeuwijk, M. & Holzner, M. 2018 Inhomogeneous growth of fluctuations of concentration of inertial particles in channel turbulence. Phys. Rev. Fluids 3 (6), 064301.Google Scholar
Frankel, A., Pouransari, H., Coletti, F. & Mani, A. 2016 Settling of heated particles in homogeneous turbulence. J. Fluid Mech. 792, 869–893.Google Scholar
Garcia-Villalba, M., Kidanemariam, A. G. & Uhlmann, M. 2012 DNS of vertical plane channel flow with finite-size particles: Voronoi analysis, acceleration statistics and particle-conditioned averaging. Intl J. Multiphase Flow 46, 54–74.Google Scholar
Gondret, P., Lance, M. & Petit, L. 2002 Bouncing motion of spherical particles in fluids. Phys. Fluids 14 (2), 643–652.Google Scholar
Goto, S. & Vassilicos, J. C. 2008 Sweep-stick mechanism of heavy particle clustering in fluid turbulence. Phys. Rev. Lett. 100 (5), 054503.Google Scholar
Gualtieri, P., Picano, F. & Casciola, C. M. 2009 Anisotropic clustering of inertial particles in homogeneous shear flow. J. Fluid Mech. 629, 25–39.Google Scholar
Gualtieri, P., Picano, F., Sardina, G. & Casciola, C. M. 2015 Exact regularized point particle method for multiphase flows in the two-way coupling regime. J. Fluid Mech. 773, 520–561.Google Scholar
Guha, A. 2008 Transport and deposition of particles in turbulent and laminar flow. Annu. Rev. Fluid Mech. 40, 311–341.Google Scholar
Gustavsson, K. & Mehlig, B. 2016 Statistical models for spatial patterns of heavy particles in turbulence. Adv. Phys. 65 (1), 1–57.Google Scholar
Hadinoto, K., Jones, E. N., Yurteri, C. & Curtis, J. S. 2005 Reynolds number dependence of gas-phase turbulence in gas–particle flows. Intl J. Multiphase Flow 31 (4), 416–434.Google Scholar
Hardalupas, Y., Taylor, A. M. K. P. & Whitelaw, J. H. 1989 Velocity and particle-flux characteristics of turbulent particle–laden jets. Proc. R. Soc. Lond. A 426 (1870), 31–78.Google Scholar
Hassan, Y. A., Blanchat, T. K., Seeley, C. H. Jr & Canaan, R. E. 1992 Simultaneous velocity measurements of both components of a two-phase flow using particle image velocimetry. Intl J. Multiphase Flow 18 (3), 371–395.Google Scholar
Holtzer, G. L. & Collins, L. R. 2002 Relationship between the intrinsic radial distribution function for an isotropic field of particles and lower-dimensional measurements. J. Fluid Mech. 459, 93–102.Google Scholar
Horwitz, J. A. K. & Mani, A. 2016 Accurate calculation of Stokes drag for point-particle tracking in two-way coupled flows. J. Comput. Phys. 318, 85–109.Google Scholar
Hrenya, C. M. & Sinclair, J. L. 1997 Effects of particle-phase turbulence in gas–solid flows. AIChE J. 43 (4), 853–869.Google Scholar
Ireland, P. J. & Desjardins, O. 2017 Improving particle drag predictions in Euler–Lagrange simulations with two-way coupling. J. Comput. Phys. 338, 405–430.Google Scholar
de Jong, J., Salazar, J. P. L. C., Woodward, S. H., Collins, L. R. & Meng, H. 2010 Measurement of inertial particle clustering and relative velocity statistics in isotropic turbulence using holographic imaging. Intl J. Multiphase Flow 36 (4), 324–332.Google Scholar
Joseph, G. G., Zenit, R., Hunt, M. L. & Rosenwinkel, A. M. 2001 Particle–wall collisions in a viscous fluid. J. Fluid Mech. 433, 329–346.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1995a Particle behavior in the turbulent boundary layer. I. Motion, deposition, and entrainment. Phys. Fluids 7 (5), 1095–1106.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1995b Particle behavior in the turbulent boundary layer. II. Velocity and distribution profiles. Phys. Fluids 7 (5), 1107–1121.Google Scholar
Khalitov, D. A. & Longmire, E. K. 2002 Simultaneous two-phase PIV by two-parameter phase discrimination. Exp. Fluids 32 (2), 252–268.Google Scholar
Khalitov, D. A. & Longmire, E. K. 2003 Effect of particle size on velocity correlations in turbulent channel flow. In ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference, pp. 445–453. American Society of Mechanical Engineers.Google Scholar
Kiger, K. T. & Pan, C. 2000 PIV technique for the simultaneous measurement of dilute two-phase flows. J. Fluids Engng 122 (4), 811–818.Google Scholar
Kiger, K. T. & Pan, C. 2002 Suspension and turbulence modification effects of solid particulates on a horizontal turbulent channel flow. J. Turbul. 3 (19), 1–17.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kleinstreuer, C. & Zhang, Z. 2010 Airflow and particle transport in the human respiratory system. Annu. Rev. Fluid Mech. 42, 301–334.Google Scholar
Knowles, P. L. & Kiger, K. T. 2012 Quantification of dispersed phase concentration using light sheet imaging methods. Exp. Fluids 52 (3), 697–708.Google Scholar
Kuerten, J. G. M. & Vreman, A. W. 2015 Effect of droplet interaction on droplet-laden turbulent channel flow. Phys. Fluids 27 (5), 053304.Google Scholar
Kulick, J. D., Fessler, J. R. & Eaton, J. K. 1994 Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 277, 109–134.Google Scholar
Kussin, J. & Sommerfeld, M. 2002 Experimental studies on particle behaviour and turbulence modification in horizontal channel flow with different wall roughness. Exp. Fluids 33 (1), 143–159.Google Scholar
Li, D., Luo, K. & Fan, J. 2016 Modulation of turbulence by dispersed solid particles in a spatially developing flat-plate boundary layer. J. Fluid Mech. 802, 359–394.Google Scholar
Li, J., Wang, H., Liu, Z., Chen, S. & Zheng, C. 2012 An experimental study on turbulence modification in the near-wall boundary layer of a dilute gas–particle channel flow. Exp. Fluids 53 (5), 1385–1403.Google Scholar
Li, Y., McLaughlin, J. B., Kontomaris, K. & Portela, L. 2001 Numerical simulation of particle–laden turbulent channel flow. Phys. Fluids 13 (10), 2957–2967.Google Scholar
Lin, Z.-w., Shao, X.-m., Yu, Z.-s. & Wang, L.-p. 2017 Effects of finite-size heavy particles on the turbulent flows in a square duct. Hydrodynamics 29 (2), 272–282.Google Scholar
Liu, B. Y. H. & Agarwal, J. K. 1974 Experimental observation of aerosol deposition in turbulent flow. Aerosol Sci. 5 (2), 145–155.Google Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.Google Scholar
Marchioli, C., Soldati, A., Kuerten, J. G. M., Arcen, B., Taniere, A., Goldensoph, G., Squires, K. D., Cargnelutti, M. F. & Portela, L. M. 2008 Statistics of particle dispersion in direct numerical simulations of wall-bounded turbulence: results of an international collaborative benchmark test. Intl J. Multiphase Flow 34 (9), 879–893.Google Scholar
Masi, E., Simonin, O., Riber, E., Sierra, P. & Gicquel, L. Y. M. 2014 Development of an algebraic-closure-based moment method for unsteady Eulerian simulations of particle–laden turbulent flows in very dilute regime. Intl J. Multiphase Flow 58, 257–278.Google Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
McLaughlin, J. B. 1989 Aerosol particle deposition in numerically simulated channel flow. Phys. Fluids A 1 (7), 1211–1224.Google Scholar
Mehrabadi, M., Horwitz, J. A. K., Subramaniam, S. & Mani, A. 2018 A direct comparison of particle-resolved and point-particle methods in decaying turbulence. J. Fluid Mech. 850, 336–369.Google Scholar
Meneguz, E. & Reeks, M. W. 2011 Statistical properties of particle segregation in homogeneous isotropic turbulence. J. Fluid Mech. 686, 338–351.Google Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2010 Preferential concentration of heavy particles: a Voronoï analysis. Phys. Fluids 22 (10), 103304.Google Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2012 Analyzing preferential concentration and clustering of inertial particles in turbulence. Intl J. Multiphase Flow 40, 1–18.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.Google Scholar
Nasr, H., Ahmadi, G. & McLaughlin, J. B. 2009 A DNS study of effects of particle–particle collisions and two-way coupling on particle deposition and phasic fluctuations. J. Fluid Mech. 640, 507–536.Google Scholar
Nicolai, C., Jacob, B. & Piva, R. 2013 On the spatial distribution of small heavy particles in homogeneous shear turbulence. Phys. Fluids 25 (8), 083301.Google Scholar
Nilsen, C., Andersson, H. I. & Zhao, L. 2013 A Voronoï analysis of preferential concentration in a vertical channel flow. Phys. Fluids 25 (11), 115108.Google Scholar
Niño, Y. & Garcia, M. H. 1996 Experiments on particle–turbulence interactions in the near-wall region of an open channel flow: implications for sediment transport. J. Fluid Mech. 326, 285–319.Google Scholar
Ohmi, K. & Li, H.-Y. 2000 Particle-tracking velocimetry with new algorithms. Meas. Sci. Technol. 11 (6), 603–616.Google Scholar
Oliveira, J. L. G., van der Geld, C. W. M. & Kuerten, J. G. M. 2017 Concentration and velocity statistics of inertial particles in upward and downward pipe flow. J. Fluid Mech. 822, 640–663.Google Scholar
Pan, Y. & Banerjee, S. 1996 Numerical simulation of particle interactions with wall turbulence. Phys. Fluids 8 (10), 2733–2755.Google Scholar
Paris, A. D.2001 Turbulence attenuation in a particle–laden channel flow. PhD thesis, Stanford University, Stanford, CA.Google Scholar
Petersen, A. J., Baker, L. & Coletti, F. 2019 Experimental study of inertial particles clustering and settling in homogeneous turbulence. J. Fluid Mech. 864, 925–970.Google Scholar
Picano, F., Breugem, W.-P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rabencov, B., Arca, J. & van Hout, R. 2014 Measurement of polystyrene beads suspended in a turbulent square channel flow: spatial distributions of velocity and number density. Intl J. Multiphase Flow 62, 110–122.Google Scholar
Reeks, M. W. 1983 The transport of discrete particles in inhomogeneous turbulence. Aerosol Sci. 14 (6), 729–739.Google Scholar
Reeks, M. W. 2014 Transport, mixing and agglomeration of particles in turbulent flows. Flow Turbul. Combust. 92, 3–25.Google Scholar
Richter, D. H. & Sullivan, P. P. 2013 Momentum transfer in a turbulent, particle–laden Couette flow. Phys. Fluids 25 (5), 053304.Google Scholar
Richter, D. H. & Sullivan, P. P. 2014 Modification of near-wall coherent structures by inertial particles. Phys. Fluids 26 (10), 103304.Google Scholar
Righetti, M. & Romano, G. P. 2004 Particle–fluid interactions in a plane near-wall turbulent flow. J. Fluid Mech. 505, 93–121.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Rouson, D. W. I. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428, 149–169.Google Scholar
Sahu, S., Hardalupas, Y. & Taylor, A. M. K. P. 2014 Droplet–turbulence interaction in a confined polydispersed spray: effect of droplet size and flow length scales on spatial droplet–gas velocity correlations. J. Fluid Mech. 741, 98–138.Google Scholar
Sahu, S., Hardalupas, Y. & Taylor, A. M. K. P. 2016 Droplet–turbulence interaction in a confined polydispersed spray: effect of turbulence on droplet dispersion. J. Fluid Mech. 794, 267–309.Google Scholar
Salazar, J. P. L. C., De Jong, J., Cao, L., Woodward, S. H., Meng, H. & Collins, L. R. 2008 Experimental and numerical investigation of inertial particle clustering in isotropic turbulence. J. Fluid Mech. 600, 245–256.Google Scholar
Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C. M. 2012a Wall accumulation and spatial localization in particle–laden wall flows. J. Fluid Mech. 699, 50–78.Google Scholar
Sardina, G., Schlatter, P., Picano, F., Casciola, C. M., Brandt, L. & Henningson, D. S. 2012b Self-similar transport of inertial particles in a turbulent boundary layer. J. Fluid Mech. 706, 584–596.Google Scholar
Schneiders, L., Meinke, M. & Schröder, W. 2017 Direct particle–fluid simulation of Kolmogorov-length-scale size particles in decaying isotropic turbulence. J. Fluid Mech. 819, 188–227.Google Scholar
Shokri, R., Ghaemi, S., Nobes, D. S. & Sanders, R. S. 2017 Investigation of particle–laden turbulent pipe flow at high-Reynolds-number using particle image/tracking velocimetry (PIV/PTV). Intl J. Multiphase Flow 89, 136–149.Google Scholar
Soldati, A. & Marchioli, C. 2009 Physics and modelling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 35 (9), 827–839.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3 (5), 1169–1178.Google Scholar
Sumbekova, S., Cartellier, A., Aliseda, A. & Bourgoin, M. 2017 Preferential concentration of inertial sub-Kolmogorov particles: the roles of mass loading of particles, Stokes numbers, and Reynolds numbers. Phys. Rev. Fluids 2 (2), 024302.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic particle–laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.Google Scholar
Sundaram, S. & Collins, L. R. 1999 A numerical study of the modulation of isotropic turbulence by suspended particles. J. Fluid Mech. 379, 105–143.Google Scholar
Taniere, A., Oesterle, B. & Monnier, J. C. 1997 On the behaviour of solid particles in a horizontal boundary layer with turbulence and saltation effects. Exp. Fluids 23 (6), 463–471.Google Scholar
Vance, M. W., Squires, K. D. & Simonin, O. 2006 Properties of the particle velocity field in gas–solid turbulent channel flow. Phys. Fluids 18 (6), 063302.Google Scholar
Varaksin, A. Y., Polezhaev, Y. V. & Polyakov, A. F. 2000 Effect of particle concentration on fluctuating velocity of the disperse phase for turbulent pipe flow. Intl J. Heat Fluid Flow 21 (5), 562–567.Google Scholar
Vreman, A. W. 2007 Turbulence characteristics of particle–laden pipe flow. J. Fluid Mech. 584, 235–279.Google Scholar
Vreman, A. W. 2015 Turbulence attenuation in particle–laden flow in smooth and rough channels. J. Fluid Mech. 773, 103–136.Google Scholar
Wang, G., Abbas, M. & Climent, É. 2017 Modulation of large-scale structures by neutrally buoyant and inertial finite-size particles in turbulent Couette flow. Phys. Rev. Fluids 2 (8), 084302.Google Scholar
Wang, G. & Richter, D. 2019 Modulation of the turbulence regeneration cycle by inertial particles in planar Couette flow. J. Fluid Mech. 861, 901–929.Google Scholar
Wang, L.-P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Wei, T., Schmidt, R. & McMurtry, P. 2005 Comment on the Clauser chart method for determining the friction velocity. Exp. Fluids 38 (5), 695–699.Google Scholar
Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71 (2), 186–192.Google Scholar
Wood, A. M., Hwang, W. & Eaton, J. K. 2005 Preferential concentration of particles in homogeneous and isotropic turbulence. Intl J. Multiphase Flow 31 (10–11), 1220–1230.Google Scholar
Wu, Y., Wang, H., Liu, Z., Li, J., Zhang, L. & Zheng, C. 2006 Experimental investigation on turbulence modification in a horizontal channel flow at relatively low mass loading. Acta Mech. Sin. 22 (2), 99–108.Google Scholar
Yang, T. S. & Shy, S. S. 2005 Two-way interaction between solid particles and homogeneous air turbulence: particle settling rate and turbulence modification measurements. J. Fluid Mech. 526, 171–216.Google Scholar
Young, J. & Leeming, A. 1997 A theory of particle deposition in turbulent pipe flow. J. Fluid Mech. 340, 129–159.Google Scholar
Zamansky, R., Coletti, F., Massot, M. & Mani, A. 2016 Turbulent thermal convection driven by heated inertial particles. J. Fluid Mech. 809, 390–437.Google Scholar
Zhang, H. & Ahmadi, G. 2000 Aerosol particle transport and deposition in vertical and horizontal turbulent duct flows. J. Fluid Mech. 406, 55–80.Google Scholar
Zhao, L. H., Andersson, H. I. & Gillissen, J. J. J. 2010 Turbulence modulation and drag reduction by spherical particles. Phys. Fluids 22 (8), 081702.Google Scholar