A parametric study is conducted for the control of a turbulent jet using a single unsteady minijet. A number of control parameters that influence the decay rate $K$ of the jet centreline mean velocity are investigated, including the mass flow rate ratio $C_{m}$, excitation frequency ratio $f_{e}/f_{0}$ and exit diameter ratio $d/D$ of the minijet to main jet, along with the duty cycle ($\unicode[STIX]{x1D6FC}$) of the minijet injection. Extensive hot-wire, particle image velocimetry and flow visualization measurements were performed in the manipulated jet. Various flow structures have been identified, such as the flapping flow, non-flapping flow and that showing a manipulable thrust vector, depending on $C_{m}$, $f_{e}/f_{0}$ and $\unicode[STIX]{x1D6FC}$. Empirical scaling analysis unveils that, prior to the minijet impingement upon the wall of the nozzle and the generation of turbulence, the relationship $K=g_{1}$ ($C_{m}$, $f_{e}/f_{0}$, $d/D$, $\unicode[STIX]{x1D6FC}$) may be reduced to $K=g_{2}$ ($\unicode[STIX]{x1D709}$), where $g_{1}$ and $g_{2}$ are different functions and the scaling factor $\unicode[STIX]{x1D709}=(\sqrt{MR}/\unicode[STIX]{x1D6FC})(d/D)^{n}$ ($\sqrt{MR}\equiv C_{m}(D/d)$ is the momentum ratio and $n$ is a constant that depends on $\unicode[STIX]{x1D6FC}$) is physically the effective momentum ratio per pulse or effective penetration depth. Discussion is conducted based on $K=g_{2}$ ($\unicode[STIX]{x1D709}$), which provides important insight into the jet control physics.

The transition to turbulence in the rotating disk boundary layer is investigated in a closed cylindrical rotor–stator cavity via direct numerical simulation (DNS) and linear stability analysis (LSA). The mean flow in the rotor boundary layer is qualitatively similar to the von Kármán self-similarity solution. The mean velocity profiles, however, slightly depart from theory as the rotor edge is approached. Shear and centrifugal effects lead to a locally more unstable mean flow than the self-similarity solution, which acts as a strong source of perturbations. Fluctuations start rising there, as the Reynolds number is increased, eventually leading to an edge-driven global mode, characterized by spiral arms rotating counter-clockwise with respect to the rotor. At larger Reynolds numbers, fluctuations form a steep front, no longer driven by the edge, and followed downstream by a saturated spiral wave, eventually leading to incipient turbulence. Numerical results show that this front results from the superposition of several elephant front-forming global modes, corresponding to unstable azimuthal wavenumbers $m$, in the range $m\in [32,78]$. The spatial growth along the radial direction of the energy of these fluctuations is quantitatively similar to that observed experimentally. This superposition of elephant modes could thus provide an explanation for the discrepancy observed in the single disk configuration, between the corresponding spatial growth rates values measured by experiments on the one hand, and predicted by LSA and DNS performed in an azimuthal sector, on the other hand.

We conduct direct numerical simulations for turbulent Rayleigh–Bénard (RB) convection, driven simultaneously by two scalar components (say, temperature and concentration) with different molecular diffusivities, and measure the respective fluxes and the Reynolds number. To account for the results, we generalize the Grossmann–Lohse theory for traditional RB convection (Grossmann & Lohse, J. Fluid Mech., vol. 407, 2000, pp. 27–56; Phys. Rev. Lett., vol. 86 (15), 2001, pp. 3316–3319; Stevens et al., J. Fluid Mech., vol. 730, 2013, pp. 295–308) to this two-scalar turbulent convection. Our numerical results suggest that the generalized theory can successfully capture the overall trends for the fluxes of two scalars and the Reynolds number without introducing any new free parameters. In fact, for most of the parameter space explored here, the theory can even predict the absolute values of the fluxes and the Reynolds number with good accuracy. The current study extends the generality of the Grossmann–Lohse theory in the area of buoyancy-driven convection flows.

The development of the unsteady pressure field on the floor of a rectangular cavity was studied at Mach 0.9 using high-frequency pressure-sensitive paint. Power spectral amplitudes at each cavity resonance exhibit a spatial distribution with a streamwise-oscillatory pattern; additional maxima and minima appear as the mode number is increased. This spatial distribution also appears in the propagation velocity of modal pressure disturbances. This behaviour was tied to the superposition of a downstream-propagating shear-layer disturbance and an upstream-propagating acoustic wave of different amplitudes and convection velocities, consistent with the classical Rossiter model. The summation of these waves generates a net downstream-travelling wave whose amplitude and phase velocity are modulated by a fixed envelope within the cavity. This travelling-wave interpretation of the Rossiter model correctly predicts the instantaneous modal pressure behaviour in the cavity. Subtle spanwise variations in the modal pressure behaviour were also observed, which could be attributed to a shift in the resonance pattern as a result of spillage effects at the edges of the finite-width cavity.

Steady Boussinesq flow in a weakly curved channel driven by a horizontal temperature gradient is considered. Linear variation in the transverse direction is assumed so that the problem reduces to a system of ordinary differential equations. A series expansion in $G$, a parameter proportional to the Grashof number and the square root of the curvature, reveals a real singularity and anticipates hysteresis. Numerical solutions are found using path continuation and the bifurcation diagrams for different parameter values are obtained. Multivalued solutions are observed as $G$ and the Prandtl number vary. Often fields with the imposed structure that satisfy all the governing equations are insensitive to the boundary conditions and can be regarded as perturbations of the homogeneous (or ‘unforced’) problem. Four such unforced solutions are found. In two of these the velocity remains coupled with temperature which, formally, scales as $1/G$ as $G\rightarrow 0$. The other two are purely hydrodynamic. The existence of such solutions is due to the unbounded nature of the domain. It is shown that these occur not only for the Dean equations, but constitute previously unreported solutions of the full Navier–Stokes equations in an annulus of arbitrary curvature. Two additional unforced solutions are found for large curvature.

We study the settling of rigid oblates in a quiescent fluid using interface-resolved direct numerical simulations. In particular, an immersed boundary method is used to account for the dispersed solid phase together with lubrication correction and collision models to account for short-range particle–particle interactions. We consider semi-dilute suspensions of oblate particles with aspect ratio 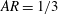$AR=1/3$ and solid volume fractions 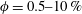$\unicode[STIX]{x1D719}=0.5{-}10\,\%$. The solid-to-fluid density ratio 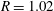$R=1.02$ and the Galileo number (i.e. the ratio between buoyancy and viscous forces) based on the diameter of a sphere with equivalent volume 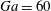$Ga=60$. With this choice of parameters, an isolated oblate falls vertically with a steady wake with its broad side perpendicular to the gravity direction. At this 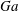$Ga$, the mean settling speed of spheres is a decreasing function of the volume 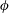$\unicode[STIX]{x1D719}$ and is always smaller than the terminal velocity of the isolated particle, 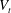$V_{t}$. On the contrary, in dilute suspensions of oblate particles (with 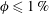$\unicode[STIX]{x1D719}\leqslant 1\,\%$), the mean settling speed is approximately 33 % larger than 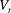$V_{t}$. At higher concentrations, the mean settling speed decreases becoming smaller than the terminal velocity 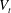$V_{t}$ between 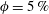$\unicode[STIX]{x1D719}=5\,\%$ and 10 %. The increase of the mean settling speed is due to the formation of particle clusters that for 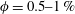$\unicode[STIX]{x1D719}=0.5{-}1\,\%$ appear as columnar-like structures. From the pair distribution function we observe that it is most probable to find particle pairs almost vertically aligned. However, the pair distribution function is non-negligible all around the reference particle indicating that there is a substantial amount of clustering at radial distances between 2 and 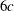$6c$ (with $c$ the polar radius of the oblate). Above 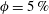$\unicode[STIX]{x1D719}=5\,\%$, the hindrance becomes the dominant effect, and the mean settling speed decreases below 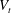$V_{t}$. As the particle concentration increases, the mean particle orientation changes and the mean pitch angle (the angle between the particle axis of symmetry and gravity) increases from 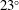$23^{\circ }$ to 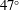$47^{\circ }$. Finally, we increase 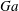$Ga$ from 60 to 140 for the case with 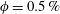$\unicode[STIX]{x1D719}=0.5\,\%$ and find that the mean settling speed (normalized by 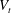$V_{t}$) decreases by less than 1 % with respect to 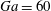$Ga=60$. However, the fluctuations of the settling speed around the mean are reduced and the probability of finding vertically aligned particle pairs increases.

Polymer-containing solutions used across research and industry are commonly exposed to mechanically harsh fluid processes, for example shear and extensional forces during flow through porous media or rapid microdispensing of biopharmaceutical molecules. These forces are strong enough to break the covalent bonds in the polymer backbone. As this scission phenomenon can change the functional and fluid-flow properties as well as introduce reactive radicals into the solution, it must be understood and controlled. Experiments and models to date have only provided partial or qualitative insights into this behaviour. Here we build a link between the molecular-scale degradation models and the macroscale laminar flow of dilute solutions in any given geometry. A free-draining bead–rod model is used to investigate rupture events at the molecular scale. It is shown by uniaxial extension simulations of an ensemble of chains that scission can be conveniently described at the macroscopic scale as a first-order reaction whose rate is a function of the conformation tensor of the macromolecules and the velocity gradient of the flow. This approach is implemented in the finite volume code OpenFOAM by elaborating an appropriate constitutive equation for the conformation tensor. The macroscopic model is run and analysed for ultra-dilute solutions of poly(methyl methacrylate) in ethyl acetate and polyethylene oxide in water, using the geometry of an abrupt contraction flow and neglecting any viscoelastic effect. This multiscale approach bridges the gap between phenomenological observations of mechanically induced chemical degradation in large-scale applications and the rich field of molecular-scale models of macromolecules under flow.

Direct numerical simulations of temporally evolving reacting compressible mixing layers have been performed to study the viscous superlayer (VSL) at the outer edge of the interface layer. Budgets of the transport equation of enstrophy conditioned on the normal distance from the turbulent/non-turbulent interface are used to examine the features of the VSL. A new method is introduced to detect and to quantify the thickness of the VSL in reacting compressible flows. It involves finding the correlation coefficient of the viscous diffusion term with the viscous dissipation term. It is shown that, while compressibility seems to have little effect on the thickness of the VSL, as the level of heat release increases, the thickness of this layer decreases. Furthermore, it is observed that a thinner VSL propagates slower, resulting in a decrease of the rate of entrainment into the mixing layer.

The behaviour of steady transonic dense gas flow is essentially governed by two non-dimensional parameters characterising the magnitude and sign of the fundamental derivative of gas dynamics ($\unicode[STIX]{x1D6E4}$) and its derivative with respect to the density at constant entropy ($\unicode[STIX]{x1D6EC}$) in the small-disturbance limit. The resulting response to external forcing is surprisingly rich and studied in detail for the canonical problem of two-dimensional flow past compression/expansion ramps.

A group of three multiscale inhomogeneous grids have been tested to generate different types of turbulent shear flows with different mean shear rate and turbulence intensity profiles. Cross hot-wire measurements were taken in a wind tunnel with Reynolds number $Re_{D}$ of 6000–20 000, based on the width of the vertical bars of the grid and the incoming flow velocity. The effect of local drag coefficient $C_{D}$ on the mean velocity profile is discussed first, and then by modifying the vertical bars to obtain a uniform aspect ratio the mean velocity profile is shown to be predictable using the local blockage ratio profile. It is also shown that, at a streamwise location $x=x_{m}$, the turbulence intensity profile along the vertical direction $u^{\prime }(y)$ scales with the wake interaction length $x_{\ast ,n}^{peak}=0.21g_{n}^{2}/(\unicode[STIX]{x1D6FC}C_{D}w_{n})$ ($\unicode[STIX]{x1D6FC}$ is a constant characterizing the incoming flow condition, and $g_{n}$, $w_{n}$ are the gap and width of the vertical bars, respectively, at layer $n$) such that $(u^{\prime }/U_{n})^{2}\unicode[STIX]{x1D6FD}^{2}(C_{D}w_{n}/x_{\ast ,n}^{peak})^{-1}\sim (x_{m}/x_{\ast ,n}^{peak})^{b}$, where $\unicode[STIX]{x1D6FD}$ is a constant determined by the free-stream turbulence level, $U_{n}$ is the local mean velocity and $b$ is a dimensionless power law constant. A general framework of grid design method based on these scalings is proposed and discussed. From the evolution of the shear stress coefficient $\unicode[STIX]{x1D70C}(x)$, integral length scale $L(x)$ and the dissipation coefficient $C_{\unicode[STIX]{x1D716}}(x)$, a simple turbulent kinetic energy model is proposed that describes the evolution of our grid generated turbulence field using one centreline measurement and one vertical profile of $u^{\prime }(y)$ at the beginning of the evolution. The results calculated from our model agree well with our measurements in the streamwise extent up to $x/H\approx 2.5$, where $H$ is the height of the grid, suggesting that it might be possible to design some shear flows with desired mean velocity and turbulence intensity profiles by designing the geometry of a passive grid.

When a drop impacts on a liquid surface its bottom is deformed by lubrication pressure and it entraps a thin disc of air, thereby making contact along a ring at a finite distance from the centreline. The outer edge of this contact moves radially at high speed, governed by the impact velocity and bottom radius of the drop. Then at a certain radial location an ejecta sheet emerges from the neck connecting the two liquid masses. Herein, we show the formation of an azimuthal instability at the base of this ejecta, in the sharp corners at the two sides of the ejecta. They promote regular radial vorticity, thereby breaking the axisymmetry of the motions on the finest scales. The azimuthal wavenumber grows with the impact Weber number, based on the bottom curvature of the drop, reaching over 400 streamwise streaks around the periphery. This instability occurs first at Reynolds numbers ($Re$) of ${\sim}7000$, but for larger $Re$ is overtaken by the subsequent axisymmetric vortex shedding and their interactions can form intricate tangles, loops or chains.

Small perturbations to a steady uniform granular chute flow can grow as the material moves downslope and develop into a series of surface waves that travel faster than the bulk flow. This roll wave instability has important implications for the mitigation of hazards due to geophysical mass flows, such as snow avalanches, debris flows and landslides, because the resulting waves tend to merge and become much deeper and more destructive than the uniform flow from which they form. Natural flows are usually highly polydisperse and their dynamics is significantly complicated by the particle size segregation that occurs within them. This study investigates the kinematics of such flows theoretically and through small-scale experiments that use a mixture of large and small glass spheres. It is shown that large particles, which segregate to the surface of the flow, are always concentrated near the crests of roll waves. There are different mechanisms for this depending on the relative speed of the waves, compared to the speed of particles at the free surface, as well as on the particle concentration. If all particles at the surface travel more slowly than the waves, the large particles become concentrated as the shock-like wavefronts pass them. This is due to a concertina-like effect in the frame of the moving wave, in which large particles move slowly backwards through the crest, but travel quickly in the troughs between the crests. If, instead, some particles on the surface travel more quickly than the wave and some move slower, then, at low concentrations, large particles can move towards the wave crest from both the forward and rearward sides. This results in isolated regions of large particles that are trapped at the crest of each wave, separated by regions where the flow is thinner and free of large particles. There is also a third regime arising when all surface particles travel faster than the waves, which has large particles present everywhere but with a sharp increase in their concentration towards the wave fronts. In all cases, the significantly enhanced large particle concentration at wave crests means that such flows in nature can be especially destructive and thus particularly hazardous.

The velocity gradient tensor for turbulent flow contains crucial information on the topology of turbulence, vortex stretching and the dissipation of energy. A Schur decomposition of the velocity gradient tensor (VGT) is introduced to supplement the standard decomposition into rotation and strain tensors. Thus, the normal parts of the tensor (represented by the eigenvalues) are separated explicitly from non-normality. Using a direct numerical simulation of homogeneous isotropic turbulence, it is shown that the norm of the non-normal part of the tensor is of a similar magnitude to the normal part. It is common to examine the second and third invariants of the characteristic equation of the tensor simultaneously (the $\unicode[STIX]{x1D64C}{-}\unicode[STIX]{x1D64D}$ diagram). With the Schur approach, the discriminant function separating real and complex eigenvalues of the VGT has an explicit form in terms of strain and enstrophy: where eigenvalues are all real, enstrophy arises from the non-normal term only. Re-deriving the evolution equations for enstrophy and total strain highlights the production of non-normality and interaction production (normal straining of non-normality). These cancel when considering the evolution of the VGT in terms of its eigenvalues but are important for the full dynamics. Their properties as a function of location in $\unicode[STIX]{x1D64C}{-}\unicode[STIX]{x1D64D}$ space are characterized. The Schur framework is then used to explain two properties of the VGT: the preference to form disc-like rather than rod-like flow structures, and the vorticity vector and strain alignments. In both cases, non-normality is critical for explaining behaviour in vortical regions.

A walker is a fluid entity comprising a bouncing droplet coupled to the waves that it generates at the surface of a vibrated bath. Thanks to this coupling, walkers exhibit a series of wave–particle features formerly thought to be exclusive to the quantum realm. In this paper, we derive a model of the Faraday surface waves generated by an impact upon a vertically vibrated liquid surface. We then particularise this theoretical framework to the case of forcing slightly below the Faraday instability threshold. Among others, this theory yields a rationale for the cosine dependence of the wave amplitude to the phase shift between impact and forcing, as well as the characteristic time scale and length scale of viscous damping. The theory is validated with experiments of bead impact on a vibrated bath. We finally discuss implications of these results for the analogy between walkers and quantum particles.

Understanding what shapes the drop size distributions produced from fluid fragmentation is important for a range of industrial, natural and health processes. Gilet & Bourouiba (J. R. Soc. Interface, vol. 12, 2015, 20141092) showed that both the size and speed of fragmented droplets are critical to transmission of pathogens in the agricultural context. In this paper, we study both the size and speed distributions of droplets ejected during a canonical unsteady sheet fragmentation from drop impact on a target of comparable size to that of the drop. Upon impact, the drop transforms into a sheet which expands in the air bounded by a rim on which ligaments grow, continuously shedding droplets. We developed high-precision tracking algorithms that capture all ejected droplets, measuring their size and speed, as well as the detachment time from, and link to, their ligament of origin. Both size and speed distributions of all ejected droplets are skewed. We show that the polydispersity and skewness of the distributions are inherently due to the unsteadiness of the sheet expansion. We show that each ligament sheds a single drop at a time throughout the entire sheet expansion by a mechanism of end-pinching. The droplet-to-ligament size ratio $R\approx 1.5$ remains constant throughout the unsteady fragmentation, and is robust to change in impact Weber number. We also show that the population mean speed of the fragmented droplets at a given time is equal to the population mean speed of ligaments one necking time prior to detachment time.

The question of causality is pervasive to fluid–structure interactions, where it finds its most alluring instance in the study of fish swimming in coordination. How and why fish align their bodies, synchronize their motion, and position in crystallized formations are yet to be fully understood. Here, we posit a model-free approach to infer causality in fluid–structure interactions through the information-theoretic notion of transfer entropy. Given two dynamical units, transfer entropy quantifies the reduction of uncertainty in predicting the future state of one of them due to additional knowledge about the past of the other. We demonstrate our approach on a system of two tandem airfoils in a uniform flow, where the pitch angle of one airfoil is actively controlled while the other is allowed to passively rotate. Through transfer entropy, we seek to unveil causal relationships between the airfoils from information transfer conducted by the fluid medium.

This article presents a framework for building analytical solutions for coupled flow in two interacting multiphase domains. The coupled system consists of a multiphase sphere embedded in a multiphase substrate. Each of these domains consists of an interconnected, load-bearing, creeping matrix phase and an inviscid, interstitial fluid phase. This article outlines techniques for building analytical solutions for velocity, pressure and compaction within each domain, subject to boundary conditions of continuity of matrix velocity, normal traction, normal pressure gradient, and compaction at the interface between the two domains. The solutions, valid over a short period of time in the limit of small fluid fraction, are strongly dependent on the ratio of shear viscosities between the matrix phase in the sphere and the matrix phase in the substrate. Compaction and pressure drop across the interface, evaluated at the poles and the equator, are strongly dependent on the ratio of matrix shear viscosities in the two domains. When deformed under a pure shear deformation, the magnitude of flow within the sphere rapidly decreases with an increase in this ratio until it reaches a value of ${\sim}80$, after which the velocity within the sphere becomes relatively insensitive to the increase in the viscosity ratio.

Flow past two circular cylinders in cruciform arrangement is simulated by direct numerical simulations for Reynolds numbers ranging from 100 to 500. The study is aimed at investigating the local flow pattern near the gap between the two cylinders, the global vortex shedding flow in the wake of the cylinders and their effects on the force coefficients of the two cylinders. The three identified local flow patterns near the gap: trail vortex (TV), necklace vortex (NV) and vortex shedding in the gap (SG) agree with those found by flow visualization in experimental studies. As for the global wake flow, two modes of vortex shedding are identified: K mode with inclined wake vortices and P mode where the wake vortices are parallel to the cylinders. The K mode occurs when the gap is slightly greater than the boundary gap between the NV and SG. It also coexists with the SG gap flow pattern if the Reynolds number is very small ($Re=100$). The flow pattern affects the force coefficient. The K mode increases the mean drag coefficient and the standard deviation of the lift coefficient at the centre of the upstream cylinder because the wake vortices converge towards the centre. The mean drag coefficient and standard deviation of the lift coefficient of the downstream cylinder decreases because of the shedding effect from the upstream cylinder.

Fluid flow in microchannels has wide industrial and scientific applications. Hence, it is important to explore different driving mechanisms. In this paper, we study the net transport or fluid pumping in a two-dimensional channel induced by a travelling temperature wave applied at the bottom wall. The Navier–Stokes equations with the Boussinesq approximation and the convection–diffusion heat equation are made dimensionless by the height of the channel and a velocity scale obtained by a dominant balance between buoyancy and viscous resistance in the momentum equation. The system of equations is transformed to an axial coordinate that moves with the travelling temperature wave, and we seek steady solutions in this moving frame. Four dimensionless numbers emerge from the governing equations and boundary conditions: the Reynolds number $Re$, a Reynolds number $Rc$ based on the wave speed, the Prandtl number $Pr$ and the dimensionless wavenumber $K$. The system of equations is solved by a finite-volume method and by a perturbation method in the limit $Re\rightarrow 0$. Surprisingly, the leading and first-order perturbation solutions agree well with the computed axial flow for $Re\leqslant 10^{3}$. Thus, the analytic perturbation solutions are used to study systematically the effects of $Re$, $Rc$, $Pr$ and $K$ on the dimensionless induced axial flow $Q$. We find that $Q$ varies linearly with $Re$, and $Q/Re$ versus any of the three remaining dimensionless groups always exhibits a maximum. The global maximum of $Q/Re$ in the parameter space is subsequently determined for the first time. This induced axial flow is driven solely by the Reynolds stress.

One of the classic analytical predictions of shoaling-wave amplification is Green’s law – the wave amplitude grows proportional to $h^{-1/4}$, where $h$ is the local water depth. Green’s law is valid for linear shallow-water waves unidirectionally propagating in a gradually varying water depth. On the other hand, conservation of mechanical energy shows that the shoaling-wave amplitude of a solitary wave grows like $a\propto h^{-1}$, if the waveform maintains its solitary-wave identity. Nonetheless, some recent laboratory and field measurements indicate that growth of long waves during shoaling is slower than what is predicted by Green’s law. Obvious missing factors in Green’s law are the nonlinearity and frequency-dispersion effects as well as wave reflection from the beach, whereas the adiabatic shoaling process does not recognize the transformation of the waveform on a beach of finite slope and length. Here we first examine this problem analytically based on the variable-coefficient perturbed Korteweg–de Vries equation. Three analytical solutions for different limits are obtained: (1) Green’s law for the linear and non-dispersive limit, (2) the slower amplitude growth rate for the linear and dispersive limit, as well as (3) nonlinear and non-dispersive limit. Then, in order to characterize the shoaling behaviours for a variety of incident wave and beach conditions, we implement a fifth-order pseudo-spectral numerical model for the full water-wave Euler theory. We found that Green’s law is not the norm but is limited to small incident-wave amplitudes when the wavelength is still small in comparison to the beach length scale. In general, the wave amplification rate during shoaling does not follow a power law. When the incident wave is finite, the shoaling amplification becomes faster than that of Green’s law when the ratio of the wavelength to the beach length is small, but becomes slower when the length ratio increases. We also found that the incident wave starts to amplify prior to its crest arriving at the beach toe due to the wave reflection. Other prominent characteristics and behaviours of solitary-wave shoaling are discussed.