Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-21T11:02:59.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition to turbulence in the rotating disk boundary layer of a rotor–stator cavity

Published online by Cambridge University Press:  08 June 2018

Eunok Yim ,
J.-M. Chomaz ,
D. Martinand Open the ORCID record for D. Martinand [Opens in a new window]  and
E. Serre Open the ORCID record for E. Serre [Opens in a new window]
Eunok Yim
Affiliation:
Aix-Marseille Univ., CNRS, Centrale Marseille, M2P2 Marseille, France
J.-M. Chomaz
Affiliation:
LadHyX, CNRS-Ecole Polytechnique, F-91128 Palaiseau, France
D. Martinand
Affiliation:
Aix-Marseille Univ., CNRS, Centrale Marseille, M2P2 Marseille, France
E. Serre*
Affiliation:
Aix-Marseille Univ., CNRS, Centrale Marseille, M2P2 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The transition to turbulence in the rotating disk boundary layer is investigated in a closed cylindrical rotor–stator cavity via direct numerical simulation (DNS) and linear stability analysis (LSA). The mean flow in the rotor boundary layer is qualitatively similar to the von Kármán self-similarity solution. The mean velocity profiles, however, slightly depart from theory as the rotor edge is approached. Shear and centrifugal effects lead to a locally more unstable mean flow than the self-similarity solution, which acts as a strong source of perturbations. Fluctuations start rising there, as the Reynolds number is increased, eventually leading to an edge-driven global mode, characterized by spiral arms rotating counter-clockwise with respect to the rotor. At larger Reynolds numbers, fluctuations form a steep front, no longer driven by the edge, and followed downstream by a saturated spiral wave, eventually leading to incipient turbulence. Numerical results show that this front results from the superposition of several elephant front-forming global modes, corresponding to unstable azimuthal wavenumbers 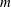$m$, in the range 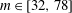$m\in [32,78]$. The spatial growth along the radial direction of the energy of these fluctuations is quantitatively similar to that observed experimentally. This superposition of elephant modes could thus provide an explanation for the discrepancy observed in the single disk configuration, between the corresponding spatial growth rates values measured by experiments on the one hand, and predicted by LSA and DNS performed in an azimuthal sector, on the other hand.

JFM classification

Instability: Nonlinear instability Geophysical and Geological Flows: Rotating flows Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 631 - 647
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2015 Global linear instability of the rotating-disk flow investigated through simulations. J. Fluid Mech. 765, 612–631.Google Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2016 On the global nonlinear instability of the rotating-disk flow over a finite domain. J. Fluid Mech. 803, 332–355.Google Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2018 Transition to turbulence in the rotating-disk boundary-layer flow with stationary vortices. J. Fluid Mech. 836, 4371.CrossRefGoogle Scholar
Batchelor, G. K. 1951 Note on a class of solutions of the Navier–Stokes equations representing steady rotationally-symmetric flow. Q. J. Mech. Appl. Maths 4, 29–41.Google Scholar
Bödewadt, U. T. 1940 Die drehströmung über festem grunde. Z. Angew. Math. Mech. 20, 241–253.CrossRefGoogle Scholar
Couairon, A. & Chomaz, J. M. 1996 Global instability in fully nonlinear systems. Phys. Rev. Lett. 77 (19), 4015–4018.Google Scholar
Cros, A., Floriani, E., Le Gal, P. & Lima, R. 2005 Transition to turbulence of the batchelor flow in a rotor/stator device. Eur. J. Mech. (B/Fluids) 24, 409–424.Google Scholar
Davies, C. & Carpenter, P. W. 2003 Global behaviour corresponding to the absolute instability of the rotating-disk boundary layer. J. Fluid Mech. 486, 287–329.Google Scholar
Davies, C., Thomas, C. & Carpenter, P. W. 2007 Global stability of the rotating-disk boundary layer. J. Engng Maths 57, 219–236.Google Scholar
Dimarogonas, A. D., Paipetis, S. A. & Chondros, T. G. 2013 Flow-Induced Vibration of Rotating Shafts. Springer.Google Scholar
Healey, J. J. 2010 Model for unstable global modes in the rotating-disk boundary layer. J. Fluid Mech. 663, 148–159.CrossRefGoogle Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2013 An experimental study of the edge effects on rotating-disk transition. J. Fluid Mech. 716, 638–657.Google Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2014 On the laminar-turbulent transition of the rotating-disk flow: the role of absolute instability. J. Fluid Mech. 745, 132–163.Google Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2016 Experimental study of rotatind-disk boundary-layer flow with surface roughness. J. Fluid Mech. 786, 5–28.Google Scholar
von Kármán, Th. 1921 Über laminare und turbulente Reibung. Z. Angew. Math. Mech. 1, 233–252.Google Scholar
Kobayashi, R., Kohama, Y. & Takamadate, Ch. 1980 Spiral vortices in boundary layer transition regime on a rotating disk. Acta Mech. 35 (1), 71–82.Google Scholar
Launder, B. E., Poncet, S. & Serre, E. 2010 Laminar, transitional, and turbulent flows in rotor–stator cavities. Ann. Rev. Fluid Mech. 42, 229–248.Google Scholar
Lingwood, R. J. 1995 Absolute instability of the boundary layer on a rotating disk. J. Fluid Mech. 299, 17–33.Google Scholar
Lingwood, R. J. 1996 An experimental study of the absolute instability of the rotating-disk boundary-layer flow. J. Fluid Mech. 314, 373–405.Google Scholar
Lingwood, R. J. 1997 Absolute instability of the Ekman layer and related rotating flows. J. Fluid Mech. 331, 405–428.CrossRefGoogle Scholar
Othman, H. & Corke, T. C. 2006 Experimental investigation of absolute instability of a rotating-disk boundary layer. J. Fluid Mech. 565, 63–94.Google Scholar
Owen, J. M. & Rogers, R. H. 1989 Heat Transfer in Rotating-Disk System: Rotor–Stator Systems.(ed. Morris, W. D.), vol. 1. Wiley.Google Scholar
Peres, N., Poncet, S. & Serre, E. 2012 A 3d pseudospectral method for cylindrical coordinates. application to the simulations of rotating cavity flows. J. Comput. Phys. 231 (19), 6290–6305.Google Scholar
Pier, B. 2003 Finite amplitude crossflow vortices, secondary instability and transition in the rotating-disk boundary layer. J. Fluid Mech. 487, 315–343.Google Scholar
Pier, B. 2013 Transition near the edge of a rotating disk. J. Fluid Mech. 737, R1.Google Scholar
Serre, E., Crespo del Arco, E. & Bontoux, P. 2001 Annular and spiral patterns in flows between rotating and stationary discs. J. Fluid Mech. 434, 65–100.Google Scholar
Serre, E., Tuliszka-Sznitko, E. & Bontoux, P. 2004 Coupled numerical and theoretical study of the flow transition between a rotating and a stationary disk. Phys. Fluids 16, 688–706.Google Scholar
Severac, E. & Serre, E. 2007 A spectral vanishing viscosity for the les of turbulent flows within rotating cavities. J. Comput. Phys. 226, 1234–1255.Google Scholar
Viaud, B., Serre, E. & Chomaz, J. M. 2008 The elephant mode between two rotating disks. J. Fluid Mech. 598, 451–464.Google Scholar
Viaud, B., Serre, E. & Chomaz, J. M. 2011 Transition to turbulence through steep global-modes cascade in an open rotating cavity. J. Fluid Mech. 688, 493–506.CrossRefGoogle Scholar