Article contents
Analytical solution for two-phase flow within and outside a sphere under pure shear
Published online by Cambridge University Press: 13 June 2018
Abstract
This article presents a framework for building analytical solutions for coupled flow in two interacting multiphase domains. The coupled system consists of a multiphase sphere embedded in a multiphase substrate. Each of these domains consists of an interconnected, load-bearing, creeping matrix phase and an inviscid, interstitial fluid phase. This article outlines techniques for building analytical solutions for velocity, pressure and compaction within each domain, subject to boundary conditions of continuity of matrix velocity, normal traction, normal pressure gradient, and compaction at the interface between the two domains. The solutions, valid over a short period of time in the limit of small fluid fraction, are strongly dependent on the ratio of shear viscosities between the matrix phase in the sphere and the matrix phase in the substrate. Compaction and pressure drop across the interface, evaluated at the poles and the equator, are strongly dependent on the ratio of matrix shear viscosities in the two domains. When deformed under a pure shear deformation, the magnitude of flow within the sphere rapidly decreases with an increase in this ratio until it reaches a value of 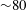 ${\sim}80$, after which the velocity within the sphere becomes relatively insensitive to the increase in the viscosity ratio.
${\sim}80$, after which the velocity within the sphere becomes relatively insensitive to the increase in the viscosity ratio.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 1
- Cited by



