Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-21T11:19:46.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Early azimuthal instability during drop impact

Published online by Cambridge University Press:  13 June 2018

E. Q. Li ,
M.-J. Thoraval Open the ORCID record for M.-J. Thoraval [Opens in a new window] ,
J. O. Marston Open the ORCID record for J. O. Marston [Opens in a new window]  and
S. T. Thoroddsen Open the ORCID record for S. T. Thoroddsen [Opens in a new window]
E. Q. Li
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, PR China
M.-J. Thoraval
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia State Key Laboratory for Strength and Vibration of Mechanical Structures, Shaanxi Key Laboratory of Environment and Control for Flight Vehicle, International Center for Applied Mechanics, School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, PR China
J. O. Marston
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia Department of Chemical Engineering, Texas Tech University, Lubbock, TX 79409-3121, USA
S. T. Thoroddsen*
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology (KAUST), Thuwal, 23955-6900, Saudi Arabia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When a drop impacts on a liquid surface its bottom is deformed by lubrication pressure and it entraps a thin disc of air, thereby making contact along a ring at a finite distance from the centreline. The outer edge of this contact moves radially at high speed, governed by the impact velocity and bottom radius of the drop. Then at a certain radial location an ejecta sheet emerges from the neck connecting the two liquid masses. Herein, we show the formation of an azimuthal instability at the base of this ejecta, in the sharp corners at the two sides of the ejecta. They promote regular radial vorticity, thereby breaking the axisymmetry of the motions on the finest scales. The azimuthal wavenumber grows with the impact Weber number, based on the bottom curvature of the drop, reaching over 400 streamwise streaks around the periphery. 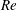This instability occurs first at Reynolds numbers ($Re$) of 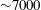${\sim}7000$, but for larger 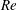$Re$ is overtaken by the subsequent axisymmetric vortex shedding and their interactions can form intricate tangles, loops or chains.

JFM classification

Interfacial Flows (free surface): Capillary flows Drops and Bubbles: Drops and Bubbles Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 821 - 835
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agbaglah, G., Josserand, C. & Zaleski, S. 2013 Longitudinal instability of a liquid rim. Phys. Fluids 25, 022103.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bouwhuis, W., van der Veen, R. C. A., Tran, T., Keij, D. L., Winkels, K. G., Peters, I. R., van der Meer, D., Sun, C., Snoeijer, J. H. & Lohse, D. 2012 Maximal air bubble entrainment at liquid-drop impact. Phys. Rev. Lett. 109, 264501.CrossRefGoogle ScholarPubMed
Castrejon-Pita, A. A., Castrejon-Pita, J. R. & Hutchings, I. M. 2012 Experimental observation of von Karman vortices during drop impact. Phys. Rev. E 86, 045301(R).Google Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81, 1131–1198.CrossRefGoogle Scholar
Crooks, J., Marsh, B., Turchetta, R., Taylor, K., Chan, W., Lahav, A. & Fenigstein, A. 2013 Kirana: a solid-state megapixel uCMOS image sensor for ultrahigh speed imaging. Proc. SPIE 8659, 865903.Google Scholar
Deegan, R. D., Brunet, P. & Eggers, J. 2008 Complexities of splashing. Nonlinearity 21, C1–C11.Google Scholar
Etoh, T. G. et al. 2003 An image sensor which captures 100 consecutive frames at 1000000 frames/s. IEEE Trans. Electron Devices 50, 144–151.Google Scholar
Gordillo, J. M., Lhuissier, H. & Villermaux, E. 2014 On the cusps bordering liquid sheets. J. Fluid Mech. 754, R1.CrossRefGoogle Scholar
Hendrix, M. H. W., Bouwhuis, W., Van Der Meer, D., Lohse, D. & Snoeijer, J. H. 2016 Universal mechanism for air entrainment during liquid impact. J. Fluid Mech. 789, 708–725.CrossRefGoogle Scholar
Hicks, P. D., Ermanyuk, E. V., Gavrilov, N. V. & Purvis, R. 2012 Air trapping at impact of a rigid sphere onto a liquid. J. Fluid Mech. 695, 310–320.Google Scholar
Hicks, P. D. & Purvis, R. 2010 Air cushioning and bubble entrapment in three-dimensional droplet impacts. J. Fluid Mech. 649, 135–163.Google Scholar
Howison, S. D., Ockendon, J. R., Oliver, J. M., Purvis, R. & Smith, F. T. 2005 Droplet impact on a thin fluid layer. J. Fluid Mech. 542, 1–23.Google Scholar
Josserand, C. & Thoroddsen, S. T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48, 365–391.Google Scholar
Josserand, C. & Zaleski, S. 2003 Droplet splashing on a thin liquid film. Phys. Fluids 15, 1650–1657.CrossRefGoogle Scholar
Korobkin, A. A. 2007 Second-order Wagner theory of wave impact. J. Engng Maths 58, 121–139.CrossRefGoogle Scholar
Korobkin, A. A., Ellis, A. S. & Smith, F. T. 2008 Trapping of air in impact between a body and shallow water. J. Fluid Mech. 611, 365–394.Google Scholar
Korobkin, A. A. & Scolan, Y. M. 2006 Three-dimensional theory of water impact. Part 2. Linearized Wagner problem. J. Fluid Mech. 549, 343–373.Google Scholar
Li, E. Q. & Thoroddsen, S. T. 2015 Time-resolved imaging of a compressible air disc under a drop impacting on a solid surface. J. Fluid Mech. 780, 636–648.CrossRefGoogle Scholar
Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2011 Bubble entrapment during sphere impact onto quiescent liquid surfaces. J. Fluid Mech. 680, 660–670.Google Scholar
Moore, M. R., Ockendon, H., Ockendon, J. R. & Oliver, J. M. 2014 Capillary and viscous perturbations to Helmholtz flows. J. Fluid Mech. 742, R1.CrossRefGoogle Scholar
Oliver, J. M.2002 Water entry and related problems. PhD thesis, Oxford University.Google Scholar
Peck, B. & Sigurdson, L. 1998 On the kinematics at a free surface. IMA J. Appl. Maths 61, 1–13.CrossRefGoogle Scholar
Philippi, J., Lagrée, P.-Y. & Antkowiak, A. 2016 Drop impact on a solid surface: short-time self-similarity. J. Fluid Mech. 795, 96–135.Google Scholar
Prosperetti, A., Crum, L. A. & Pumphrey, H. C. 1989 The underwater noise of rain. J. Geophys. Res. 94 (C3), 3255–3259.CrossRefGoogle Scholar
Reyssat, E. & Quéré, D. 2006 Bursting of a fluid film in a viscous environment. Europhys. Lett. 76 (2), 236–242.Google Scholar
Riboux, G. & Gordillo, J. M. 2014 Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113, 024507.Google Scholar
Rioboo, R., Marengo, M. & Tropea, C. 2002 Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 33, 112–124.Google Scholar
Scolan, Y. M. & Korobkin, A. A. 2001 Three-dimensional theory of water impact. Part 1. Inverse Wagner problem. J. Fluid Mech. 440, 293–326.Google Scholar
Semenov, Y. A., Wu, G. X. & Korobkin, A. A. 2015 Impact of liquids with different densities. J. Fluid Mech. 766, 5–27.Google Scholar
Thoraval, M.-J., Takehara, K., Etoh, T. G., Popinet, S., Ray, P., Josserand, C., Zaleski, S. & Thoroddsen, S. T. 2012 Von Kármán vortex street within an impacting drop. Phys. Rev. Lett. 108, 264506.Google Scholar
Thoraval, M.-J., Takehara, K., Etoh, T. G. & Thoroddsen, S. T. 2013 Drop impact entrapment of bubble rings. J. Fluid Mech. 724, 234–258.CrossRefGoogle Scholar
Thoroddsen, S. T. 2002 The ejecta sheet generated by the impact of a drop. J. Fluid Mech. 451, 373–381.CrossRefGoogle Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2008 High-speed imaging of drops and bubble. Annu. Rev. Fluid Mech. 40, 257–285.CrossRefGoogle Scholar
Thoroddsen, S. T., Takehara, K. & Etoh, T. G. 2012a Micro-splashing by drop impacts. J. Fluid Mech. 706, 560–570.Google Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2003 Air entrapment under an impacting drop. J. Fluid Mech. 478, 125–134.Google Scholar
Thoroddsen, S. T., Thoraval, M.-J., Takehara, K. & Etoh, T. G. 2012b Micro-bubble morphologies following drop impacts onto a pool surface. J. Fluid Mech. 708, 469–479.Google Scholar
Tran, T., De Maleprade, H., Sun, C. & Lohse, D. 2013 Air entrainment during impact of droplets on liquid surfaces. J. Fluid Mech. 726, R3.Google Scholar
Villermaux, E. 2007 Fragmentation. Annu. Rev. Fluid Mech. 39, 419–446.Google Scholar
Wagner, H. 1932 Uber Stoss- und Gleitvorgange an der Oberflache von Flussigkeiten. Z. Angew. Math. Mech. 12, 193–215.Google Scholar
Weiss, D. A. & Yarin, A. L. 1999 Single drop impact onto liquid films: neck distortion, jetting, tiny bubble entrainment, and crown formation. J. Fluid Mech. 385, 229–254.Google Scholar
Worthington, A. M. 1908 A Study of Splashes. Longmans, Green and Co.Google Scholar
Zhang, L. V., Brunet, P., Eggers, J. & Deegan, R. D. 2010 Wavelength selection in the crown splash. Phys. Fluids 22, 122105.Google Scholar
Zhang, L. V., Toole, J., Fezzaa, K. & Deegan, R. D. 2012 Evolution of the ejecta sheet from the impact of a drop with a deep pool. J. Fluid Mech. 690, 5–15.CrossRefGoogle Scholar

Li et al. supplementary movie 1

Movie 1: Video corresponding to Figure 4(a). The frame rate is 500 kfps.

Download Li et al. supplementary movie 1(Video)
Video 6.5 MB
Supplementary material: PDF

Li et al. supplementary material

Supplementary material

Download Li et al. supplementary material(PDF)
PDF 1.6 MB

Li et al. supplementary movie 2

Movie 2: Video corresponding to Figure 4(b). The frame rate is 2 million fps.

Download Li et al. supplementary movie 2(Video)
Video 19.2 MB

Li et al. supplementary movie 3

Movie 3: Video corresponding to Figure 5(a). The frame rate is 2 million fps.

Download Li et al. supplementary movie 3(Video)
Video 8.9 MB

Li et al. supplementary movie 4

Movie 4: Video corresponding to Figure 5(b). The frame rate is 2 million fps.

Download Li et al. supplementary movie 4(Video)
Video 12.3 MB

Li et al. supplementary movie 5

Movie 5: Video corresponding to Figure 8(a). The frame rate is 1 million fps.

Download Li et al. supplementary movie 5(Video)
Video 9.2 MB

Li et al. supplementary movie 6

Movie 6: Video showing close-up of radial and axial vortices, with entrapment of bubble rings. Impact height is 59 cm and pixel resolution is 1 micron/px. The frame rate is 1 million fps.

Download Li et al. supplementary movie 6(Video)
Video 16.9 MB