Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T16:39:18.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Parametric study and scaling of jet manipulation using an unsteady minijet

Published online by Cambridge University Press:  08 June 2018

A. K. Perumal Open the ORCID record for A. K. Perumal [Opens in a new window]  and
Y. Zhou
A. K. Perumal
Affiliation:
Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, 518055, China
Y. Zhou*
Affiliation:
Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, 518055, China Digital Engineering Laboratory of Offshore Equipment, Shenzhen, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

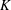A parametric study is conducted for the control of a turbulent jet using a single unsteady minijet. A number of control parameters that influence the decay rate $K$ of the jet centreline mean velocity are investigated, including the mass flow rate ratio 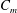$C_{m}$, excitation frequency ratio 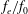$f_{e}/f_{0}$ and exit diameter ratio 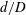$d/D$ of the minijet to main jet, along with the duty cycle ($\unicode[STIX]{x1D6FC}$) of the minijet injection. Extensive hot-wire, particle image velocimetry and flow visualization measurements were performed in the manipulated jet. Various flow structures have been identified, such as the flapping flow, non-flapping flow and that showing a manipulable thrust vector, depending on 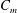$C_{m}$, 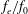$f_{e}/f_{0}$ and $\unicode[STIX]{x1D6FC}$. Empirical scaling analysis unveils that, prior to the minijet impingement upon the wall of the nozzle and the generation of turbulence, the relationship 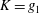$K=g_{1}$ (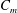$C_{m}$, 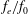$f_{e}/f_{0}$, 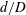$d/D$, $\unicode[STIX]{x1D6FC}$) may be reduced to 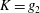$K=g_{2}$ (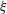$\unicode[STIX]{x1D709}$), where 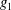$g_{1}$ and 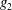$g_{2}$ are different functions and the scaling factor 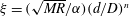$\unicode[STIX]{x1D709}=(\sqrt{MR}/\unicode[STIX]{x1D6FC})(d/D)^{n}$ (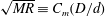$\sqrt{MR}\equiv C_{m}(D/d)$ is the momentum ratio and $n$ is a constant that depends on $\unicode[STIX]{x1D6FC}$) is physically the effective momentum ratio per pulse or effective penetration depth. Discussion is conducted based on 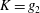$K=g_{2}$ (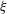$\unicode[STIX]{x1D709}$), which provides important insight into the jet control physics.

JFM classification

Flow Control: Flow Control Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 592 - 630
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alkislar, M. B., Krothapalli, A. & Butler, G. 2007 The effect of streamwise vortices on the aeroacoustics of a Mach 0.9 jet. J. Fluid Mech. 578, 139–169.Google Scholar
Ball, C. G., Fellouah, H. & Pollard, A. 2012 The flow field in turbulent round free jets. Prog. Aerosp. Sci. 50, 1–26.Google Scholar
Behrouzi, P., Feng, T. & McGuirk, J. J. 2008 Active flow control of jet mixing using steady and pulsed fluid tabs. Proc. Inst. Mech. Engrs 222, 381–392.Google Scholar
Bradbury, L. J. S. & Khadem, A. H. 1975 The distortion of a jet by tabs. J. Fluid Mech. 70, 801–813.CrossRefGoogle Scholar
Breidenthal, R. E., Tong, K. O., Wong, G. S., Hamerquist, R. D. & Landry, P. B. 1985 Turbulent mixing in two-dimensional ducts with transverse jets. AIAA J. 21 (11), 1867–1869.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large scale structures in turbulent mixing layers. J. Fluid Mech. 64, 775–816.CrossRefGoogle Scholar
Bons, J. P., Sondergaard, R. & Rivir, R. B. 2001 The fluid dynamics of LPT blade separation control using pulsed jets. J. Turbomach. 124 (1), 77–85.CrossRefGoogle Scholar
Cattafesta, L. N. III & Sheplak, M. 2011 Actuators for active flow control. Annu. Rev. Fluid Mech. 43, 247–272.Google Scholar
Chauvet, N., Deck, S. & Jacquin, L. 2007 Numerical study of mixing enhancement in a supersonic round jet. AIAA J. 45, 1675–1687.Google Scholar
Chue, S. H. 1975 Pressure probes for fluid measurement. Prog. Aerosp. Sci. 16, 147–223.CrossRefGoogle Scholar
Coussement, A., Gicquel, O. & Degrez, G. 2012 Large Eddy simulation of pulsed jet in cross flow. J. Fluid Mech. 695, 1–34.Google Scholar
Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48, 547–591.CrossRefGoogle Scholar
Davis, M. 1982 Variable control of jet decay. AIAA J. 20, 606–609.CrossRefGoogle Scholar
Edwards, A. C., Sherman, W. D. & Breidenthal, R. E. 1985 Turbulent mixing in tubes with transverse injection. AIChE J. 31, 516–518.Google Scholar
Eroglu, A. & Breidenthal, R. E. 2001 Structure, penetration, and mixing of pulsed jets in crossflow. AIAA J. 39, 417–423.CrossRefGoogle Scholar
Fan, D. W., Wu, Z., Yang, H., Li, J. D. & Zhou, Y. 2017 A modified extremum seeking closed-loop system for jet mixing enhancement. AIAA J. 55, 3891–3902.Google Scholar
Freund, J. B. & Moin, P. 2000 Jet mixing enhancement by high-amplitude fluidic actuation. AIAA J. 38, 1863–1870.Google Scholar
Gutmark, E. & Grinstein, F. 1999 Flow control with noncircular jets. Annu. Rev. Fluid Mech. 31, 239–272.Google Scholar
Gutmark, E. & Ho, C. M. 1983 Preferred modes and the spreading rates of jets. Phys. Fluids 26, 2932–2938.CrossRefGoogle Scholar
Hermanson, J. C., Wahba, A. & Johari, H. 1998 Duty-cycle effects on penetration of fully modulated, turbulent jets in crossflow. AIAA J. 36, 1935–1937.CrossRefGoogle Scholar
Ho, C. M. & Huang, L. S. 1982 Subharmonics and vortex merging in mixing layers. J. Fluid Mech. 119, 443–473.Google Scholar
Huang, H., Dabiri, D. & Gharib, M. 1997 On errors of digital particle image velocimetry. Meas. Sci. Technol. 8, 1427–1440.Google Scholar
Huang, J. F., Zhou, Y. & Zhou, T. M. 2006 Three-dimensional wake structure measurement using a modified PIV technique. Exp. Fluids 40, 884–896.CrossRefGoogle Scholar
Huang, J. M. & Hsiao, F. B. 1999 On the mode development in the developing region of a plane jet. Phys. Fluids 11, 1847–1857.CrossRefGoogle Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.Google Scholar
Husain, H. S & Hussain, A. K. M. F. 1983 Controlled excitation of elliptic jets. Phys. Fluids 26, 2763–2766.CrossRefGoogle Scholar
Ibrahim, M. K., Kunimura, R. & Nakamura, Y. 2002 Mixing enhancement of compressible jets by using unsteady microjets as actuators. AIAA J. 40, 681–688.CrossRefGoogle Scholar
Iio, S., Hirashita, K., Katayama, Y., Haneda, Y., Ikeda, T. & Uchiyama, T. 2013 Jet flapping control with acoustic excitation. J. Flow Control Meas. Vis. 1, 49–56.Google Scholar
Johari, H. 2006 Scaling of fully pulsed jets in crossflow. AIAA J. 44, 2719–2725.Google Scholar
Johari, H., Pacheco-Tougas, M. & Hermanson, J. 1999 Penetration and mixing of fully modulated turbulent jets in crossflow. AIAA J. 37, 842–850.Google Scholar
Kamran, M. A. & McGuirk, J. J. 2011 Subsonic jet mixing via active control using steady and pulsed control jets. AIAA J. 49, 712–724.Google Scholar
Karagozian, A. R. 2014 The jet in crossflow. Phys. Fluids 26, 1–47.CrossRefGoogle Scholar
Knowles, K. & Saddington, A. J. 2006 A review of jet mixing enhancement for aircraft propulsion applications. Proc. Inst. Mech. Engrs 220, 103–127.Google Scholar
Kumar, A. P., Verma, S. B. & Rathakrishnan, E. 2015 Experimental study of subsonic and sonic jets controlled by air tabs. J. Propul. Power 31, 1473–1481.Google Scholar
Lardeau, S., Lamballais, É. & Bonnet, J. P. 2002 Direct numerical simulation of a jet controlled by fluid injection. J. Turbul. 3, N2.CrossRefGoogle Scholar
Malmstrom, T. G., Kirkpatrick, A. T., Christensen, B. & Knappmiller, K. D. 1997 Centreline velocity decay measurements in low-velocity axisymmetric jets. J. Fluid Mech. 346, 363–377.Google Scholar
M’Closkey, R. T., King, J. M., Cortelezzi, L. & Karagozian, A. R. 2002 The actively controlled jet in crossflow. J. Fluid Mech. 452, 325–335.CrossRefGoogle Scholar
Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8, 1406.Google Scholar
Namer, I. & Otugen, M. V. 1988 Velocity measurements in a plane turbulent air jet at moderate Reynolds numbers. Exp. Fluids 6, 387–399.Google Scholar
New, T. H., Lim, T. T. & Luo, S. C. 2006 Effects of jet velocity profiles on a round jet in cross-flow. Exp. Fluids 40, 859–875.Google Scholar
New, T. H. & Tay, W. L.2004. Effects of circumferential microjets on the near-field behavior of a round jet. AIAA Paper 2004-092.Google Scholar
Pack, L. G. & Seifert, A. 2001 Periodic excitation for jet vectoring and enhanced spreading. J. Aircraft 38, 486–495.Google Scholar
Parekh, D., Kibens, V., Glezer, A., Wiltse, J. & Smith, D.1996 Innovative jet flow control: mixing enhancement experiments. AIAA paper 96-0308.Google Scholar
Pattenden, R. J., Turnock, S. R. & Zhang, X. 2005 Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane. Exp. Fluids 39, 10–21.Google Scholar
Raman, G. 1997 Using controlled unsteady fluid mass addition to enhance jet mixing. AIAA J. 35, 647–656.Google Scholar
Raman, G. & Cornelius, D. 1995 Jet mixing control using excitation from miniature oscillating jets. AIAA J. 33, 365–368.Google Scholar
Raman, G., Hailye, M. & Rice, E. J. 1993 Flip–flop jet nozzle extended to supersonic flows. AIAA J. 31, 1028–1035.Google Scholar
Roshko, A. 1976 Structure of turbulent shear flows: a new look. AIAA J. 14, 1349–1357.Google Scholar
Sailor, D. J., Rohli, D. J. & Fu, Q. 1999 Effect of variable duty cycle flow pulsations on heat transfer enhancement for an impinging air jet. Intl J. Heat Fluid Flow 20, 574–580.CrossRefGoogle Scholar
Samimy, M., Kim, J.-H., Kastner, J., Adamovich, I. & Utkin, Y. 2007 Active control of high-speed and high-Reynolds-number jets using plasma actuators. J. Fluid Mech. 578, 305–330.Google Scholar
Sau, R. & Mahesh, K. 2010 Optimization of pulsed jet in crossflow. J. Fluid Mech. 653, 365–390.Google Scholar
Seidel, J. F., Pappart, C., New, T. H. & Tsai, H. M.2005 Effects of multiple radial blowing around a circular jet. AIAA Paper 2005-866.Google Scholar
Seifert, A., Darabi, A. & Wyganski, I. 1996 Delay of airfoil stall by periodic excitation. J. Aircraft 33, 691–698.Google Scholar
Shapiro, A. H. 1953 The Dynamics and Thermodynamics of Compressible Fluid Flow, vol. 1. Ronald Press.Google Scholar
Tamburello, D. A. & Amitay, M. 2007 Three-dimensional interactions of a free jet with a perpendicular synthetic jet. J. Turbul. 8, 1–21.Google Scholar
Vlasov, Ye. V. & Ginevskiy, A. S.1974 Generation and suppression of turbulence in an axisymmetric turbulent jet in the presence of an acoustic influence. Tech. Rep. TT F-15, 721. NASA.Google Scholar
Wan, C. & Yu, S. C. M. 2013 Numerical investigation of the air tabs technique in jet flow. J. Propul. Power 29, 42–49.Google Scholar
Wiltse, J. M. & Glezer, A. 1993 Manipulation of free shear flows using piezoelectric actuators. J. Fluid Mech. 249, 261–285.Google Scholar
Wickersham, P.2007 Jet mixing enhancement by high amplitude pulse-fluidic actuator. PhD thesis, Georgia Institute of Technology.Google Scholar
Yang, H.2017 Study of active jet control using unsteady minijets. PhD thesis, Harbin Institute of Technology Shenzhen Graduate School.Google Scholar
Yang, H. & Zhou, Y. 2016 Axisymmetric jet manipulated using two unsteady minijets. J. Fluid Mech. 808, 362–396.Google Scholar
Yang, H., Zhou, Y., So, R. M. C. & Liu, Y. 2016 Turbulent jet manipulation using two unsteady azimuthally separated radial minijets. Proc. R. Soc. Lond. A 472, 20160417.Google Scholar
Yu, S., Lim, K., Chao, W. & Goh, X. 2008 Mixing enhancement in subsonic jet flow using the air-tab technique. AIAA J. 46, 2966–2969.Google Scholar
Zaman, K. B. M. Q., Bridges, J. E. & Huff, D. L. 2011 Evolution from ‘tabs’ to ‘chevron technology’ – a review. Intl J. Aeroacoust. 10, 685–709.CrossRefGoogle Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1981 Turbulence suppression in free shear flows by controlled excitation. J. Fluid Mech. 103, 133–159.Google Scholar
Zhou, Y., Du, C., Mi, J. & Wang, X. 2012 Turbulent round jet control using two steady minijets. AIAA J. 50, 736–740.Google Scholar