Article contents
Numerical simulation of flow past two circular cylinders in cruciform arrangement
Published online by Cambridge University Press: 13 June 2018
Abstract
Flow past two circular cylinders in cruciform arrangement is simulated by direct numerical simulations for Reynolds numbers ranging from 100 to 500. The study is aimed at investigating the local flow pattern near the gap between the two cylinders, the global vortex shedding flow in the wake of the cylinders and their effects on the force coefficients of the two cylinders. The three identified local flow patterns near the gap: trail vortex (TV), necklace vortex (NV) and vortex shedding in the gap (SG) agree with those found by flow visualization in experimental studies. As for the global wake flow, two modes of vortex shedding are identified: K mode with inclined wake vortices and P mode where the wake vortices are parallel to the cylinders. The K mode occurs when the gap is slightly greater than the boundary gap between the NV and SG. It also coexists with the SG gap flow pattern if the Reynolds number is very small (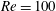 $Re=100$). The flow pattern affects the force coefficient. The K mode increases the mean drag coefficient and the standard deviation of the lift coefficient at the centre of the upstream cylinder because the wake vortices converge towards the centre. The mean drag coefficient and standard deviation of the lift coefficient of the downstream cylinder decreases because of the shedding effect from the upstream cylinder.
$Re=100$). The flow pattern affects the force coefficient. The K mode increases the mean drag coefficient and the standard deviation of the lift coefficient at the centre of the upstream cylinder because the wake vortices converge towards the centre. The mean drag coefficient and standard deviation of the lift coefficient of the downstream cylinder decreases because of the shedding effect from the upstream cylinder.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 9
- Cited by



