Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-21T11:00:47.326Z Has data issue: false hasContentIssue false
  • English
  • Français

Clustering and increased settling speed of oblate particles at finite Reynolds number

Published online by Cambridge University Press:  11 June 2018

Walter Fornari Open the ORCID record for Walter Fornari [Opens in a new window] ,
Mehdi Niazi Ardekani Open the ORCID record for Mehdi Niazi Ardekani [Opens in a new window]  and
Luca Brandt Open the ORCID record for Luca Brandt [Opens in a new window]
Walter Fornari*
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-100 44 Stockholm, Sweden
Mehdi Niazi Ardekani
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-100 44 Stockholm, Sweden
Luca Brandt
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the settling of rigid oblates in a quiescent fluid using interface-resolved direct numerical simulations. In particular, an immersed boundary method is used to account for the dispersed solid phase together with lubrication correction and collision models to account for short-range particle–particle interactions. We consider semi-dilute suspensions of oblate particles with aspect ratio 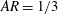$AR=1/3$ and solid volume fractions 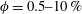$\unicode[STIX]{x1D719}=0.5{-}10\,\%$. The solid-to-fluid density ratio 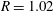$R=1.02$ and the Galileo number (i.e. the ratio between buoyancy and viscous forces) based on the diameter of a sphere with equivalent volume 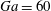$Ga=60$. With this choice of parameters, an isolated oblate falls vertically with a steady wake with its broad side perpendicular to the gravity direction. At this 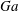$Ga$, the mean settling speed of spheres is a decreasing function of the volume 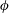$\unicode[STIX]{x1D719}$ and is always smaller than the terminal velocity of the isolated particle, 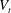$V_{t}$. On the contrary, in dilute suspensions of oblate particles (with 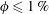$\unicode[STIX]{x1D719}\leqslant 1\,\%$), the mean settling speed is approximately 33 % larger than 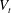$V_{t}$. At higher concentrations, the mean settling speed decreases becoming smaller than the terminal velocity 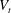$V_{t}$ between 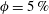$\unicode[STIX]{x1D719}=5\,\%$ and 10 %. The increase of the mean settling speed is due to the formation of particle clusters that for 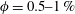$\unicode[STIX]{x1D719}=0.5{-}1\,\%$ appear as columnar-like structures. From the pair distribution function we observe that it is most probable to find particle pairs almost vertically aligned. However, the pair distribution function is non-negligible all around the reference particle indicating that there is a substantial amount of clustering at radial distances between 2 and 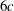$6c$ (with $c$ the polar radius of the oblate). Above 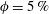$\unicode[STIX]{x1D719}=5\,\%$, the hindrance becomes the dominant effect, and the mean settling speed decreases below 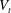$V_{t}$. As the particle concentration increases, the mean particle orientation changes and the mean pitch angle (the angle between the particle axis of symmetry and gravity) increases from 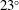$23^{\circ }$ to 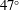$47^{\circ }$. Finally, we increase 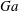$Ga$ from 60 to 140 for the case with 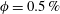$\unicode[STIX]{x1D719}=0.5\,\%$ and find that the mean settling speed (normalized by 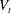$V_{t}$) decreases by less than 1 % with respect to 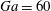$Ga=60$. However, the fluctuations of the settling speed around the mean are reduced and the probability of finding vertically aligned particle pairs increases.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 696 - 721
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ardekani, M. N., Costa, P., Breugem, W. P. & Brandt, L. 2016 Numerical study of the sedimentation of spheroidal particles. Intl J. Multiphase Flow 87, 16–34.CrossRefGoogle Scholar
Batchelor, G. K. 1972 Sedimentation in a dilute dispersion of spheres. J. Fluid Mech. 52 (02), 245–268.CrossRefGoogle Scholar
Bouchet, G., Mebarek, M. & Dušek, J. 2006 Hydrodynamic forces acting on a rigid fixed sphere in early transitional regimes. Eur. J. Mech. (B/Fluids) 25 (3), 321–336.CrossRefGoogle Scholar
Breugem, W.-P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231 (13), 4469–4498.CrossRefGoogle Scholar
Brosse, N. & Ern, P. 2011 Paths of stable configurations resulting from the interaction of two disks falling in tandem. J. Fluids Struct. 27 (5), 817–823.CrossRefGoogle Scholar
Chouippe, A. & Uhlmann, M. 2015 Forcing homogeneous turbulence in direct numerical simulation of particulate flow with interface resolution and gravity. Phys. Fluids 27 (12), 123301.CrossRefGoogle Scholar
Chrust, M.2012 Etude numérique de la chute libre d’objets axisymétriques dans un fluide Newtonien. PhD thesis, Strasbourg.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 2005 Bubbles, Drops, and Particles. Courier Corporation.Google Scholar
Climent, E. & Maxey, M. R. 2003 Numerical simulations of random suspensions at finite Reynolds numbers. Intl J. Multiphase Flow 29 (4), 579–601.CrossRefGoogle Scholar
Costa, P., Boersma, B. J., Westerweel, J. & Breugem, W.-P. 2015 Collision model for fully resolved simulations of flows laden with finite-size particles. Phys. Rev. E 92 (5), 053012.Google ScholarPubMed
Di Felice, R. 1999 The sedimentation velocity of dilute suspensions of nearly monosized spheres. Intl J. Multiphase Flow 25 (4), 559–574.CrossRefGoogle Scholar
Doostmohammadi, A. & Ardekani, A. M. 2015 Suspension of solid particles in a density stratified fluid. Phys. Fluids 27 (2), 023302.CrossRefGoogle Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid part 1. Sedimentation. J. Fluid Mech. 261, 95–134.CrossRefGoogle Scholar
Fonseca, F. & Herrmann, H. J. 2005 Simulation of the sedimentation of a falling oblate ellipsoid. Physica A 345 (3), 341–355.CrossRefGoogle Scholar
Fornari, W., Picano, F. & Brandt, L. 2016a Sedimentation of finite-size spheres in quiescent and turbulent environments. J. Fluid Mech. 788, 640–669.CrossRefGoogle Scholar
Fornari, W., Picano, F., Sardina, G. & Brandt, L. 2016b Reduced particle settling speed in turbulence. J. Fluid Mech. 808, 153–167.CrossRefGoogle Scholar
Fortes, A. F., Joseph, D. D. & Lundgren, T. S. 1987 Nonlinear mechanics of fluidization of beds of spherical particles. J. Fluid Mech. 177, 467–483.CrossRefGoogle Scholar
Garside, J. & Al-Dibouni, M. R. 1977 Velocity-voidage relationships for fluidization and sedimentation in solid–liquid systems. Ind. Engng Chem. Process Design and Development 16 (2), 206–214.CrossRefGoogle Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5 (02), 317–328.CrossRefGoogle Scholar
Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.CrossRefGoogle Scholar
Huisman, S. G., Barois, T., Bourgoin, M., Chouippe, A., Doychev, T., Huck, P., Morales, C. E. B., Uhlmann, M. & Volk, R. 2016 Columnar structure formation of a dilute suspension of settling spherical particles in a quiescent fluid. Phys. Rev. Fluids 1 (7), 074204.CrossRefGoogle Scholar
Jeffrey, D. J. 1982 Low-Reynolds-number flow between converging spheres. Mathematika 29 (1), 58–66.CrossRefGoogle Scholar
Jenny, M., Dušek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.CrossRefGoogle Scholar
Kulkarni, P. M. & Morris, J. F. 2008 Suspension properties at finite Reynolds number from simulated shear flow. Phys. Fluids 20 (4), 040602.CrossRefGoogle Scholar
Kuusela, E., Höfler, K. A. I. & Schwarzer, S. 2001 Computation of particle settling speed and orientation distribution in suspensions of prolate spheroids. J. Engng Maths 41 (2), 221–235.CrossRefGoogle Scholar
Lambert, R. A., Picano, F., Breugem, W.-P. & Brandt, L. 2013 Active suspensions in thin films: nutrient uptake and swimmer motion. J. Fluid Mech. 733, 528–557.CrossRefGoogle Scholar
Magnaudet, J. & Mougin, G. 2007 Wake instability of a fixed spheroidal bubble. J. Fluid Mech. 572, 311–337.CrossRefGoogle Scholar
Picano, F., Breugem, W.-P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.CrossRefGoogle Scholar
Richardson, J. & Zaki, W. 1954a Fluidization and sedimentation–part i. Trans. Inst. Chem. Engrs 32, 38–58.Google Scholar
Richardson, J. F. & Zaki, W. N. 1954b The sedimentation of a suspension of uniform spheres under conditions of viscous flow. Chem. Engng Sci. 3 (2), 65–73.CrossRefGoogle Scholar
Saintillan, D., Shaqfeh, E. S. G. & Darve, E. 2006 The growth of concentration fluctuations in dilute dispersions of orientable and deformable particles under sedimentation. J. Fluid Mech. 553, 347–388.CrossRefGoogle Scholar
Sangani, A. S. & Acrivos, A. 1982 Slow flow past periodic arrays of cylinders with application to heat transfer. Intl J. Multiphase Flow 8 (3), 193–206.CrossRefGoogle Scholar
Santarelli, C. & Fröhlich, J. 2015 Direct numerical simulations of spherical bubbles in vertical turbulent channel flow. Intl J. Multiphase Flow 75, 174–193.CrossRefGoogle Scholar
Santarelli, C. & Fröhlich, J. 2016 Direct numerical simulations of spherical bubbles in vertical turbulent channel flow. Influence of bubble size and bidispersity. Intl J. Multiphase Flow 81, 27–45.CrossRefGoogle Scholar
Schiller, L. & Naumann, A. 1935 A drag coefficient correlation. Vdi Zeitung 77, 318–320.Google Scholar
Shin, M., Koch, D. L. & Subramanian, G. 2009 Structure and dynamics of dilute suspensions of finite-Reynolds-number settling fibers. Phys. Fluids 21 (12), 123304.CrossRefGoogle Scholar
Tanaka, M. & Teramoto, D. 2015 Modulation of homogeneous shear turbulence laden with finite-size particles. J. Turbul. 16 (10), 979–1010.CrossRefGoogle Scholar
Uhlmann, M. & Doychev, T. 2014 Sedimentation of a dilute suspension of rigid spheres at intermediate galileo numbers: the effect of clustering upon the particle motion. J. Fluid Mech. 752, 310–348.CrossRefGoogle Scholar
Yin, X. & Koch, D. L. 2007 Hindered settling velocity and microstructure in suspensions of solid spheres with moderate Reynolds numbers. Phys. Fluids 19 (9), 093302.CrossRefGoogle Scholar
Zaidi, A. A., Tsuji, T. & Tanaka, T. 2014 Direct numerical simulation of finite sized particles settling for high Reynolds number and dilute suspension. Intl J. Heat Fluid Flow 50, 330–341.CrossRefGoogle Scholar