Research Article
Sur Les Isométries De Lp(X) Et Le Théorème Ergodique Vectoriel
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 360-391
-
- Article
-
- You have access
- Export citation
An Index Theory for Semigroups of *-Endomorphisms of
 and Type II1 Factors.
and Type II1 Factors.
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 86-114
-
- Article
-
- You have access
- Export citation
Weighted Subspaces of Hardy Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1074-1083
-
- Article
-
- You have access
- Export citation
Strong Morita Equivalence for Heisenberg C*-Algebras and the Positive Cones of Their K0-Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 833-864
-
- Article
-
- You have access
- Export citation
Spherical Homology Classes in the Bordism of Lie Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1331-1374
-
- Article
-
- You have access
- Export citation
Inequalities in Discrete Subgroups of PSL(2, R)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 115-130
-
- Article
-
- You have access
- Export citation
The Eta Invariant and Equivariant SpinC Bordism for Spherical Space form Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 392-428
-
- Article
-
- You have access
- Export citation
Choquet Boundary for Real Function Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1084-1104
-
- Article
-
- You have access
- Export citation
Pointwise Convergence of Alternating Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 610-632
-
- Article
-
- You have access
- Export citation
Semicontinuity and Multipliers of C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 865-988
-
- Article
-
- You have access
- Export citation
On Fixed Points and Multiparameter Ergodic Theorems in Banach Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 429-458
-
- Article
-
- You have access
- Export citation
On the Hankel and Some Related Transformations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 989-1009
-
- Article
-
- You have access
- Export citation
Uniform Harmonic Approximation with Continuous Extension to the Boundary
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1375-1388
-
- Article
-
- You have access
- Export citation
Tensor Products of Fundamental Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 633-648
-
- Article
-
- You have access
- Export citation
Higher Derivations and Distinguished Subfields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 131-141
-
- Article
-
- You have access
- Export citation
Linear Algebra of Curvature Tensors and Their Covariant Derivatives
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1105-1143
-
- Article
-
- You have access
- Export citation
The MOD 2 K-Homology of Ω3S3X
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 142-196
-
- Article
-
- You have access
- Export citation
On the Mapping Theorem for Lusternik-Schnirelmann Category II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1389-1398
-
- Article
-
- You have access
- Export citation
Some Remarks on IA Automorphisms of Free Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1144-1155
-
- Article
-
- You have access
- Export citation
On the Selmer Group of Twists of Elliptic Curves with Q-Rational Torsion Points
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 649-665
-
- Article
-
- You have access
- Export citation

 and Type II
and Type II and type II
and type II
 of
of 
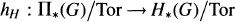
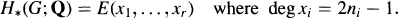
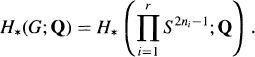
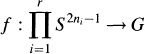
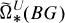 and completely detects all but the 2-primary part of the reduced equivariant Spin
and completely detects all but the 2-primary part of the reduced equivariant Spin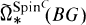 . The coefficient ring
. The coefficient ring 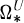 is without torsion; all the torsion in
is without torsion; all the torsion in 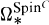 is of order 2. The prime 2 plays a distinguished role in the discussion of equivariant Spin
is of order 2. The prime 2 plays a distinguished role in the discussion of equivariant Spin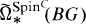 is quite different from
is quite different from 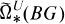 at the prime 2. Let ker
at the prime 2. Let ker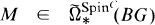 .
.  and
and 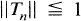 , where
, where 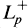 is the part of
is the part of 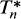 which is a positive linear contraction of
which is a positive linear contraction of 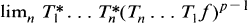
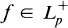 .
. , and
, and  (notation explained in Section 2), and we will call these the classes of
(notation explained in Section 2), and we will call these the classes of 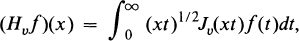
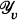 and
and 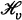 transformations defined for such
transformations defined for such 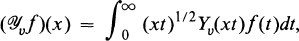
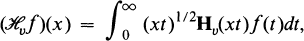
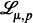 defined in [
defined in [
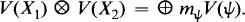
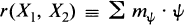



 and
and  . If we take all the known symmetries of these tensors we can define subspaces
. If we take all the known symmetries of these tensors we can define subspaces  and
and  such that
such that 



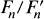 . The group
. The group 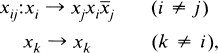
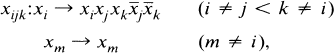
 (resp.
(resp.  ). The completion of
). The completion of  is denoted by
is denoted by  . Let
. Let  one has
one has
 . Here
. Here  and
and  is the normed valuation belonging to
is the normed valuation belonging to  . In particular
. In particular