Article contents
Pointwise Convergence of Alternating Sequences
Published online by Cambridge University Press: 20 November 2018
Extract
Let 1 < p < ∞ and let Lp be the usual Banach Space of complex valued functions on a σ-finite measure space. Let (Tn), n ≧ 1, be a sequence of positive linear contractions on Lp. Hence  and
and 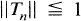 , where
, where 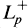 is the part of Lp that consists of non-negative Lp functions. The adjoint of Tn is denoted by
is the part of Lp that consists of non-negative Lp functions. The adjoint of Tn is denoted by 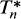 which is a positive linear contraction of Lq with q = p/(p — 1).
which is a positive linear contraction of Lq with q = p/(p — 1).
Our purpose in this paper is to show that the alternating sequences associated with (Tn), as introduced in [2], converge almost everywhere. Complete definitions will be given later. When applied to a non negative function, however, this result is reduced to the following theorem.
(1.1) THEOREM. If (Tn) is a sequence of positive contractions of Lp then (1.2) 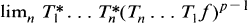
exists a.e. for all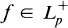 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1988
References
- 6
- Cited by


