Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Stewart, C. L.
and
Top, J.
1995.
On ranks of twists of elliptic curves and power-free values of binary forms.
Journal of the American Mathematical Society,
Vol. 8,
Issue. 4,
p.
943.
James, Kevin
1998.
L-series with nonzero central critical value.
Journal of the American Mathematical Society,
Vol. 11,
Issue. 3,
p.
635.
James, Kevin
1999.
Elliptic Curves Satisfying the Birch and Swinnerton–Dyer Conjecture mod 3.
Journal of Number Theory,
Vol. 76,
Issue. 1,
p.
16.
Bruinier, J. H.
James, K.
Kohnen, W.
Ono, K.
Skinner, C.
and
Vatsal, V.
1999.
Topics in Number Theory.
p.
115.
Vatsal, V.
1999.
Canonical periods and congruence formulae.
Duke Mathematical Journal,
Vol. 98,
Issue. 2,
Ono, K.
2001.
Nonvanishing of quadratic twists of modular L-functions and applications to elliptic curves.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2001,
Issue. 533,
Balog, Antal
and
Ono, Ken
2003.
Elements of class groups and Shafarevich-Tate groups of elliptic curves.
Duke Mathematical Journal,
Vol. 120,
Issue. 1,
Matsuno, Kazuo
2007.
Construction of elliptic curves with large Iwasawa $${\lambda}$$ -invariants and large Tate-Shafarevich groups.
manuscripta mathematica,
Vol. 122,
Issue. 3,
p.
289.
Quattrini, Patricia L.
2011.
The effect of torsion on the distribution of Ш among quadratic twists of an elliptic curve.
Journal of Number Theory,
Vol. 131,
Issue. 2,
p.
195.
Byeon, Dongho
and
Kim, Nayoung
2013.
Elliptic curves of rank zero satisfying the p-part of the Birch and Swinnerton-Dyer conjecture.
Manuscripta Mathematica,
Vol. 142,
Issue. 3-4,
p.
383.
Morrow, Jackson Salvatore
2016.
Selmer groups of twists of elliptic curves over K with K-rational torsion points.
Research in Number Theory,
Vol. 2,
Issue. 1,
Krishnamoorthy, Srilakshmi
2016.
A note on the Fourier coefficients of a Cohen–Eisenstein series.
International Journal of Number Theory,
Vol. 12,
Issue. 05,
p.
1149.
 (resp.
(resp. 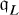 ). The completion of L with respect to
). The completion of L with respect to  is denoted by
is denoted by  . Let S be a finite set of prime numbers, and let M/L be a Galois extension with abelian Galois group of exponent p.
. Let S be a finite set of prime numbers, and let M/L be a Galois extension with abelian Galois group of exponent p. one has
one has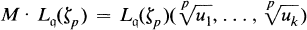
 . Here ζp is a pth root of unity, u1, …, uk are elements in
. Here ζp is a pth root of unity, u1, …, uk are elements in 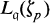 and
and  is the normed valuation belonging to
is the normed valuation belonging to  . In particular M/L is unramified at all divisors of primes q ∉ S ∪ {p}.
. In particular M/L is unramified at all divisors of primes q ∉ S ∪ {p}.

