For positive integers p$p$ and q$q$, let { \mathcal{G} }_{p, q} ${ \mathcal{G} }_{p, q}$ be a class of graphs such that \vert E(G)\vert \leq p\vert V(G)\vert - q$\vert E(G)\vert \leq p\vert V(G)\vert - q$ for every G\in { \mathcal{G} }_{p, q} $G\in { \mathcal{G} }_{p, q}$. In this paper, we consider the sum of the k\mathrm{th} $k\mathrm{th}$ powers of the degrees of the vertices of a graph G\in { \mathcal{G} }_{p, q} $G\in { \mathcal{G} }_{p, q}$ with \Delta (G)\geq 2p$\Delta (G)\geq 2p$. We obtain an upper bound for this sum that is linear in {\Delta }^{k- 1} ${\Delta }^{k- 1}$. These graphs include the planar, 1-planar, t$t$-degenerate, outerplanar, and series-parallel graphs.

In this paper, we consider the following Robin problem:

\begin{eqnarray*}\displaystyle \left\{ \begin{array}{ @{}ll@{}} \displaystyle - \Delta u= \mid x{\mathop{\mid }\nolimits }^{\alpha } {u}^{p} , \quad & \displaystyle x\in \Omega , \\ \displaystyle u\gt 0, \quad & \displaystyle x\in \Omega , \\ \displaystyle \displaystyle \frac{\partial u}{\partial \nu } + \beta u= 0, \quad & \displaystyle x\in \partial \Omega , \end{array} \right.&&\displaystyle\end{eqnarray*} $$\begin{eqnarray*}\displaystyle \left\{ \begin{array}{ @{}ll@{}} \displaystyle - \Delta u= \mid x{\mathop{\mid }\nolimits }^{\alpha } {u}^{p} , \quad & \displaystyle x\in \Omega , \\ \displaystyle u\gt 0, \quad & \displaystyle x\in \Omega , \\ \displaystyle \displaystyle \frac{\partial u}{\partial \nu } + \beta u= 0, \quad & \displaystyle x\in \partial \Omega , \end{array} \right.&&\displaystyle\end{eqnarray*}$$

\Omega $\Omega$

{ \mathbb{R} }^{N} ${ \mathbb{R} }^{N}$

N\geq 3$N\geq 3$

p\gt 1$p\gt 1$

\alpha \gt 0$\alpha \gt 0$

\beta \gt 0$\beta \gt 0$

\nu $\nu$

\partial \Omega $\partial \Omega$

\beta $\beta$

Let R$R$ be a commutative ring. The regular digraph of ideals of R$R$, denoted by \Gamma (R)$\Gamma (R)$, is a digraph whose vertex set is the set of all nontrivial ideals of R$R$ and, for every two distinct vertices I$I$ and J$J$, there is an arc from I$I$ to J$J$ whenever I$I$ contains a nonzero divisor on J$J$. In this paper, we study the connectedness of \Gamma (R)$\Gamma (R)$. We also completely characterise the diameter of this graph and determine the number of edges in \Gamma (R)$\Gamma (R)$, whenever R$R$ is a finite direct product of fields. Among other things, we prove that R$R$ has a finite number of ideals if and only if \mathrm {N}_{\Gamma (R)}(I)$\mathrm {N}_{\Gamma (R)}(I)$ is finite, for all vertices I$I$ in \Gamma (R)$\Gamma (R)$, where \mathrm {N}_{\Gamma (R)}(I)$\mathrm {N}_{\Gamma (R)}(I)$ is the set of all adjacent vertices to I$I$ in \Gamma (R)$\Gamma (R)$.

A space Y$Y$ is called an extension of a space X$X$ if Y$Y$ contains X$X$ as a dense subspace. An extension Y$Y$ of X$X$ is called a one-point extension of X$X$ if Y\setminus X$Y\setminus X$ is a singleton. P. Alexandroff proved that any locally compact non-compact Hausdorff space X$X$ has a one-point compact Hausdorff extension, called the one-point compactification of X$X$. Motivated by this, Mrówka and Tsai [‘On local topological properties. II’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys.19 (1971), 1035–1040] posed the following more general question: For what pairs of topological properties {\mathscr P}${\mathscr P}$ and {\mathscr Q}${\mathscr Q}$ does a locally-{\mathscr P}${\mathscr P}$ space X$X$ having {\mathscr Q}${\mathscr Q}$ possess a one-point extension having both {\mathscr P}${\mathscr P}$ and {\mathscr Q}${\mathscr Q}$? Here, we provide an answer to this old question.

A semigroup 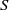S$S$ is called idempotent-surjective (respectively, regular-surjective) if whenever 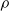\rho $\rho$ is a congruence on 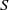S$S$ and 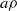a\rho $a\rho$ is idempotent (respectively, regular) in 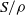S/ \rho $S/ \rho$, then there is 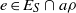e\in {E}_{S} \cap a\rho $e\in {E}_{S} \cap a\rho$ (respectively, 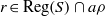r\in \mathrm{Reg} (S)\cap a\rho $r\in \mathrm{Reg} (S)\cap a\rho$), where 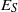{E}_{S} ${E}_{S}$ (respectively, 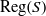\mathrm{Reg} (S)$\mathrm{Reg} (S)$) denotes the set of all idempotents (respectively, regular elements) of 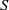S$S$. Moreover, a semigroup 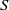S$S$ is said to be idempotent-regular-surjective if it is both idempotent-surjective and regular-surjective. We show that any regular congruence on an idempotent-regular-surjective (respectively, regular-surjective) semigroup is uniquely determined by its kernel and trace (respectively, the set of equivalence classes containing idempotents). Finally, we prove that all structurally regular semigroups are idempotent-regular-surjective.

Let { \mathcal{T} }_{X} ${ \mathcal{T} }_{X}$ be the full transformation semigroup on a set X$X$ and E$E$ be a nontrivial equivalence relation on X$X$. Denote

\begin{eqnarray*}{T}_{\exists } (X)= \{ f\in { \mathcal{T} }_{X} : \forall x, y\in X, (f(x), f(y))\in E\Rightarrow (x, y)\in E\} ,\end{eqnarray*} $$\begin{eqnarray*}{T}_{\exists } (X)= \{ f\in { \mathcal{T} }_{X} : \forall x, y\in X, (f(x), f(y))\in E\Rightarrow (x, y)\in E\} ,\end{eqnarray*}$$

{T}_{\exists } (X)${T}_{\exists } (X)$

{ \mathcal{T} }_{X} ${ \mathcal{T} }_{X}$

{T}_{\exists } (X)${T}_{\exists } (X)$

For n= 1, 2, 3, \ldots $n= 1, 2, 3, \ldots$ let {S}_{n} ${S}_{n}$ be the sum of the first n$n$ primes. We mainly show that the sequence {a}_{n} = \sqrt[n]{{S}_{n} / n}~(n= 1, 2, 3, \ldots )${a}_{n} = \sqrt[n]{{S}_{n} / n}~(n= 1, 2, 3, \ldots )$ is strictly decreasing, and moreover the sequence {a}_{n+ 1} / {a}_{n} ~(n= 10, 11, \ldots )${a}_{n+ 1} / {a}_{n} ~(n= 10, 11, \ldots )$ is strictly increasing. We also formulate similar conjectures involving twin primes or partitions of integers.

In this paper we consider the statistical concept of causality in continuous time between filtered probability spaces, based on Granger’s definitions of causality. Then we consider some stable subspaces of H^p$H^p$ which contain right continuous modifications of martingales P(A \mid {\mathcal {G}}_t)$P(A \mid {\mathcal {G}}_t)$. We give necessary and sufficient conditions, in terms of statistical causality, for these spaces to coincide with H^p$H^p$. These results can be applied to extremal measures and regular weak solutions of stochastic differential equations.

We prove that any surjective isometry between unit spheres of the {\ell }^{\infty } ${\ell }^{\infty }$-sum of strictly convex normed spaces can be extended to a linear isometry on the whole space, and we solve the isometric extension problem affirmatively in this case.

The stable rank of Leavitt path algebras of row-finite graphs was computed by Ara and Pardo. In this paper we extend this to an arbitrary directed graph. In part our computation proceeds as for the row-finite case, but we also use knowledge of the row-finite setting by applying the desingularising method due to Drinen and Tomforde. In particular, we characterise purely infinite simple quotients of a Leavitt path algebra.

In this paper, we introduce the notion of weakly weighted sharing of zeros of meromorphic functions ignoring multiplicities, which extends the notion of weakly weighted sharing counting multiplicities, and we also introduce the notion of multiplicity. By using these notions, we prove some results on the uniqueness of meromorphic functions concerning differential polynomials sharing nonzero finite values. The results in this paper extend the results of Yang and Hua, Fang, and Dyavanal. In this paper, we correct defective points in the paper of Wu et al. [‘Uniqueness of meromorphic functions sharing one value’, Bull. Aust. Math. Soc. 85(2012), 280–294].

Let T(S)$T(S)$ be the Teichmüller space of a hyperbolic Riemann surface S$S$. Suppose that \mu $\mu$ is an extremal Beltrami differential at a given point \tau $\tau$ of T(S)$T(S)$ and \{ {\phi }_{n} \} $\{ {\phi }_{n} \}$ is a Hamilton sequence for \mu $\mu$. It is an open problem whether the sequence \{ {\phi }_{n} \} $\{ {\phi }_{n} \}$ is always a Hamilton sequence for all extremal differentials in \tau $\tau$. S. Wu [‘Hamilton sequences for extremal quasiconformal mappings of the unit disk’, Sci. China Ser. A 42 (1999), 1033–1042] gave a positive answer to this problem in the case where S$S$ is the unit disc. In this paper, we show that it is also true when S$S$ is a doubly-connected domain.

The aim of this work is to adapt a construction of the so-called U_{m}$U_{m}$-numbers (m\gt 1$m\gt 1$), which are extended Liouville numbers with respect to algebraic numbers of degree m$m$ but not with respect to algebraic numbers of degree less than m$m$, to the p$p$-adic frame.

In this short paper, we show that, with three exceptions, if the Wiener index of a connected graph of order n$n$ is at most (n+ 5)(n- 2)/ 2$(n+ 5)(n- 2)/ 2$, then it is traceable.

Let (R, \mathfrak{m})$(R, \mathfrak{m})$ be a Cohen–Macaulay complete local ring. We will apply an inductive argument to show that for every nonprojective locally projective maximal Cohen–Macaulay object \mathcal{X} $\mathcal{X}$ of the morphism category of R$R$ with local endomorphism ring, there exists an almost split sequence ending in \mathcal{X} $\mathcal{X}$. Regular sequences are exploited to reduce the Krull dimension of R$R$ on which the inductive argument is established. Moreover, the Auslander–Reiten translate of certain objects is described.

Let \varphi _0$\varphi _0$ and \varphi _1$\varphi _1$ be regular functions on the boundary \partial D$\partial D$ of the unit disk D$D$ in \mathbb {R}^2$\mathbb {R}^2$, such that \int _{0}^{2\pi }\varphi _1\,d\theta =0$\int _{0}^{2\pi }\varphi _1\,d\theta =0$ and \int _{0}^{2\pi }\sin \theta (\varphi _1-\varphi _0)\,d\theta =0$\int _{0}^{2\pi }\sin \theta (\varphi _1-\varphi _0)\,d\theta =0$. It is proved that there exist a linear second-order uniformly elliptic operator L$L$ in divergence form with bounded measurable coefficients and a function u$u$ in W^{1,p}(D)$W^{1,p}(D)$, 1 \lt p \lt 2$1 \lt p \lt 2$, such that Lu=0$Lu=0$ in D$D$ and with u|_{\partial D}= \varphi _0$u|_{\partial D}= \varphi _0$ and the conormal derivative \partial u/\partial N|_{\partial D}=\varphi _1$\partial u/\partial N|_{\partial D}=\varphi _1$.

We give an affirmative answer to one of the questions posed by Bourin regarding a special type of inequality referred to as subadditivity inequalities in the case of the Hilbert–Schmidt and the trace norms. We formulate the solution for arbitrary commuting positive operators, and we conjecture that it is true for all unitarily invariant norms and all commuting positive operators. New related trace inequalities are also presented.

Suppose that G$G$ is a second countable, locally compact Hausdorff groupoid with abelian stabiliser subgroups and a Haar system. We provide necessary and sufficient conditions for the groupoid {C}^{\ast } ${C}^{\ast }$-algebra to have Hausdorff spectrum. In particular, we show that the spectrum of {C}^{\ast } (G)${C}^{\ast } (G)$ is Hausdorff if and only if the stabilisers vary continuously with respect to the Fell topology, the orbit space {G}^{(0)} / G${G}^{(0)} / G$ is Hausdorff, and, given convergent sequences {\chi }_{i} \rightarrow \chi ${\chi }_{i} \rightarrow \chi$ and {\gamma }_{i} \cdot {\chi }_{i} \rightarrow \omega ${\gamma }_{i} \cdot {\chi }_{i} \rightarrow \omega$ in the dual stabiliser groupoid \widehat{S}$\widehat{S}$ where the {\gamma }_{i} \in G${\gamma }_{i} \in G$ act via conjugation, if \chi $\chi$ and \omega $\omega$ are elements of the same fibre then \chi = \omega $\chi = \omega$.

Gama and Nguyen [‘Finding short lattice vectors within Mordell’s inequality’, in: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, New York, 2008, 257–278] have presented slide reduction which is currently the best SVP approximation algorithm in theory. In this paper, we prove the upper and lower bounds for the ratios \Vert { \mathbf{b} }_{i}^{\ast } \Vert / {\lambda }_{i} (\mathbf{L} )$\Vert { \mathbf{b} }_{i}^{\ast } \Vert / {\lambda }_{i} (\mathbf{L} )$ and \Vert {\mathbf{b} }_{i} \Vert / {\lambda }_{i} (\mathbf{L} )$\Vert {\mathbf{b} }_{i} \Vert / {\lambda }_{i} (\mathbf{L} )$, where {\mathbf{b} }_{1} , \ldots , {\mathbf{b} }_{n} ${\mathbf{b} }_{1} , \ldots , {\mathbf{b} }_{n}$ is a slide reduced basis and {\lambda }_{1} (\mathbf{L} ), \ldots , {\lambda }_{n} (\mathbf{L} )${\lambda }_{1} (\mathbf{L} ), \ldots , {\lambda }_{n} (\mathbf{L} )$ denote the successive minima of the lattice \mathbf{L} $\mathbf{L}$. We define generalised slide reduction and use slide reduction to approximate i$i$-SIVP, SMP and CVP. We also present a critical slide reduced basis for blocksize 2.

We study the space of irreducible representations of a crossed product {C}^{\ast } ${C}^{\ast }$-algebra {\mathop{A\rtimes }\nolimits}_{\sigma } G${\mathop{A\rtimes }\nolimits}_{\sigma } G$, where G$G$ is a finite group. We construct a space \widetilde {\Gamma } $\widetilde {\Gamma }$ which consists of pairs of irreducible representations of A$A$ and irreducible projective representations of subgroups of G$G$. We show that there is a natural action of G$G$ on \widetilde {\Gamma } $\widetilde {\Gamma }$ and that the orbit space G\setminus \widetilde {\Gamma } $G\setminus \widetilde {\Gamma }$ corresponds bijectively to the dual of {\mathop{A\rtimes }\nolimits}_{\sigma } G${\mathop{A\rtimes }\nolimits}_{\sigma } G$.