Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T21:28:12.214Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE REGULAR DIGRAPH OF IDEALS OF COMMUTATIVE RINGS

Part of: Chain conditions, growth conditions, and other forms of finiteness Chain conditions, finiteness conditions Graph theory

Published online by Cambridge University Press:  16 October 2012

M. AFKHAMI ,
M. KARIMI  and
K. KHASHYARMANESH
M. AFKHAMI*
Affiliation:
Department of Mathematics, University of Neyshabur, PO Box 91136-899, Neyshabur, Iran (email: [email protected])
M. KARIMI
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, PO Box 1159-91775, Mashhad, Iran (email: [email protected])
K. KHASHYARMANESH
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, PO Box 1159-91775, Mashhad, Iran (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 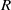$R$ be a commutative ring. The regular digraph of ideals of 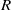$R$, denoted by 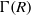$\Gamma (R)$, is a digraph whose vertex set is the set of all nontrivial ideals of 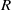$R$ and, for every two distinct vertices 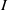$I$ and 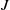$J$, there is an arc from 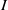$I$ to 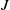$J$ whenever 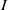$I$ contains a nonzero divisor on 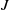$J$. In this paper, we study the connectedness of 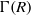$\Gamma (R)$. We also completely characterise the diameter of this graph and determine the number of edges in 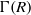$\Gamma (R)$, whenever 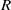$R$ is a finite direct product of fields. Among other things, we prove that 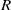$R$ has a finite number of ideals if and only if 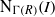$\mathrm {N}_{\Gamma (R)}(I)$ is finite, for all vertices 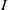$I$ in 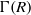$\Gamma (R)$, where 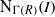$\mathrm {N}_{\Gamma (R)}(I)$ is the set of all adjacent vertices to 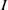$I$ in 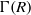$\Gamma (R)$.

Keywords

regular digraphconnectednessdiameter

MSC classification

Secondary: 05C20: Directed graphs (digraphs), tournaments 13E05: Noetherian rings and modules 16P20: Artinian rings and modules
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 177 - 189
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Afkhami, M. & Khashyarmanesh, K., ‘The cozero-divisor graph of a commutative ring’, Southeast Asian Bull. Math. 35 (2011), 753–762.Google Scholar
[2]Anderson, D. F., Axtell, M. C. & Stickles, J. A., ‘Zero-divisor graphs in commutative rings’, in: Commutative Algebra, Noetherian and Non-Noetherian Perspectives, (eds. Fontana, M., Kabbaj, S. E., Olberding, B. & Swanson, I.) (Springer, New York, 2011), pp. 23–45.CrossRefGoogle Scholar
[3]Anderson, D. F. & Livingston, P. S., ‘The zero-divisor graph of a commutative ring’, J. Algebra 217 (1999), 434–447.CrossRefGoogle Scholar
[4]Beck, I., ‘Coloring of commutative rings’, J. Algebra 116 (1998), 208–226.CrossRefGoogle Scholar
[5]Bondy, J. A & Murty, U. S. R., Graph Theory with Applications (American Elsevier, New York, 1976).CrossRefGoogle Scholar
[6]DeMeyer, F. R. & DeMeyer, L., ‘Zero-divisor graphs of semigroups’, J. Algebra 283 (2005), 190–198.CrossRefGoogle Scholar
[7]Estaji, E. & Khashyarmanesh, K., ‘The zero-divisor graph of a lattice’, Results Math. 61 (2012), 1–11.CrossRefGoogle Scholar
[8]Kelarev, A. V., Graph Algebras and Automata (Marcel Dekker, New York, 2003).CrossRefGoogle Scholar
[9]Kelarev, A. V. & Quinn, S. J., ‘A combinatorial property and power graphs of groups’, Contrib. General Algebra 12 (2000), 229–235.Google Scholar
[10]Kelarev, A. V. & Quinn, S. J., ‘Directed graphs and combinatorial properties of semigroups’, J. Algebra 251 (2002), 16–26.CrossRefGoogle Scholar
[11]Kelarev, A. V., Ryan, J. & Yearwood, J., ‘Cayley graphs as classifiers for data mining: the influence of asymmetries’, Discrete Math. 309 (2009), 5360–5369.CrossRefGoogle Scholar
[12]Li, C. H. & Praeger, C. E., ‘On the isomorphism problem for finite Cayley graphs of bounded valency’, European J. Combin. 20 (1999), 279–292.CrossRefGoogle Scholar
[13]Maimani, H. R., Salimi, M., Sattari, A. & Yassemi, S., ‘Comaximal graph of commutative rings’, J. Algebra 319 (2008), 1801–1808.CrossRefGoogle Scholar
[14]Nikmehr, M. J. & Shaveisi, F., ‘The regular digraph of ideals of a commutative ring’, Acta Math. Hunger. 134 (2012), 516–528.CrossRefGoogle Scholar
[15]Praeger, C. E., ‘Finite transitive permutation groups and finite vertex-transitive graphs’, in: Graph Symmetry: Algebraic Methods and Applications (Kluwer, Dordrecht, 1997), pp. 277–318.CrossRefGoogle Scholar
[16]Sharma, P. K. & Bhatwadekar, S. M., ‘A note on graphical representation of rings’, J. Algebra 176 (1995), 124–127.CrossRefGoogle Scholar
[17]Sharp, R. Y., Steps in Commutative Algebra, 2nd edn, London Mathematical Society Student Texts, 51 (Cambridge University Press, Cambridge, 2000).Google Scholar
[18]Thomson, A. & Zhou, S., ‘Gossiping and routing in undirected triple-loop networks’, Networks 55 (2010), 341–349.CrossRefGoogle Scholar
[19]Wang, H. J., ‘Graphs associated to co-maximal ideals of commutative rings’, J. Algebra 320 (2008), 2917–2933.CrossRefGoogle Scholar
[20]Zhou, S., ‘A class of arc-transitive Cayley graphs as models for interconnection networks’, SIAM J. Discrete Math. 23 (2009), 694–714.CrossRefGoogle Scholar