Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T08:37:34.846Z Has data issue: false hasContentIssue false
  • English
  • Français

STATISTICAL CAUSALITY AND STABLE SUBSPACES OF 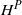$H^P$

Part of: Stochastic processes

Published online by Cambridge University Press:  01 August 2012

LJILJANA PETROVIĆ  and
DRAGANA VALJAREVIĆ
LJILJANA PETROVIĆ
Affiliation:
Department of Mathematics and Statistics, Faculty of Economics, University of Belgrade, Kamenička 6, 11000 Beograd, Serbia (email: [email protected])
DRAGANA VALJAREVIĆ*
Affiliation:
Department of Mathematics, Faculty of Science, University of Priština-Kosovska Mitrovica, Lole Ribara 29, 38220 Kosovska Mitrovica, Serbia (email: [email protected])
*
✉For correspondence; e-mail: dragana˙[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider the statistical concept of causality in continuous time between filtered probability spaces, based on Granger’s definitions of causality. Then we consider some stable subspaces of $H^p$ which contain right continuous modifications of martingales 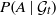$P(A \mid {\mathcal {G}}_t)$. We give necessary and sufficient conditions, in terms of statistical causality, for these spaces to coincide with 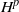$H^p$. These results can be applied to extremal measures and regular weak solutions of stochastic differential equations.

Keywords

filtrationscausalitystable subspacesextremal measuresstochastic differential equations

MSC classification

Secondary: 60G44: Martingales with continuous parameter
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 1 , August 2013 , pp. 17 - 25
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Bremaud, P. & Yor, M., ‘Changes of filtrations and of probability measures’, Z. Wahrscheinlichkeitstheorie verw. Gebiete 45 (1978), 269–295.CrossRefGoogle Scholar
[2]Gill, J. B. & Petrović, Lj., ‘Causality and stochastic dynamic systems’, SIAM J. Appl. Math. 47(6) (1987), 1361–1366.CrossRefGoogle Scholar
[3]Granger, C. W. J., ‘Investigating causal relations by econometric models and cross spectral methods’, Econometrica 37 (1969), 424–438.CrossRefGoogle Scholar
[4]Grecea, V., ‘On generating $H^p$ spaces of martingales’, Rev. Roumaine Math. Pures Appl. 53(4) (2008), 317–322.Google Scholar
[5]Jacod, J., Calcul Stochastique et Problèmes de Martingales, Lecture Notes in Mathematics (Springer, Berlin, 1979).CrossRefGoogle Scholar
[6]Kunita, H. & Watanabe, S., ‘On square integrable martingales’, Nagoya Math. J. 30 (1967), 209–245.CrossRefGoogle Scholar
[7]Medvegyev, P., Stochastic Integration Theory (Oxford University Press, Oxford, 2007).CrossRefGoogle Scholar
[8]Meyer, P. A., Probability and Potentials (North-Holland, Amsterdam, 1982).Google Scholar
[9]Mykland, P. A., ‘Statistical causality’. Statistical Report No. 14, University of Bergen, 1986.Google Scholar
[10]Mykland, P. A., ‘Stable subspaces over regular solutions of martingale problems’. Statistical Report No 15, University of Bergen, 1986.Google Scholar
[11]Petrović, Lj., ‘Causality and Markovian representations’, Statist. Probab. Lett. 29 (1996), 223–227.CrossRefGoogle Scholar
[12]Petrović, Lj. & Dimitrijević, S., ‘Invariance of statistical causality under convergence’, Statist. Probab. Lett. 81 (2011), 1445–1448.CrossRefGoogle Scholar
[13]Petrović, Lj. & Stanojević, D., ‘Some models of causality and weak solutions of stochastic differential equations with driving semimartingales’, Facta Univ. ser. 20 (2005), 103–112.Google Scholar
[14]Petrović, Lj. & Stanojević, D., ‘Statistical causality, extremal measures and weak solutions of stochastical differential equations with driving semimartingales’, J. Math. Model. Algor. 9 (2010), 113–128.CrossRefGoogle Scholar
[15]Protter, P., Stochastic Integration and Differential Equations (Springer, Berlin, 2004).Google Scholar
[16]Revuz, D. & Yor, M., Continuous Martingales and Brownian Motion (Springer, Berlin, 2005).Google Scholar
[17]Valjarević, D. & Petrović, Lj., ‘Statistical causality and orthogonality of local martingales’, Statist. Probab. Lett. 82 (2012), 1326–1330.CrossRefGoogle Scholar