Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-25T01:10:17.078Z Has data issue: false hasContentIssue false
  • English
  • Français

HAMILTON SEQUENCES FOR EXTREMAL QUASICONFORMAL MAPPINGS OF DOUBLY-CONNECTED DOMAINS

Part of: Geometric function theory

Published online by Cambridge University Press:  22 March 2013

GUOWU YAO
GUOWU YAO*
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing, 100084, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 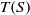$T(S)$ be the Teichmüller space of a hyperbolic Riemann surface 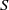$S$. Suppose that 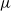$\mu $ is an extremal Beltrami differential at a given point $\tau $ of 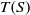$T(S)$ and 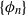$\{ {\phi }_{n} \} $ is a Hamilton sequence for 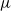$\mu $. It is an open problem whether the sequence 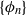$\{ {\phi }_{n} \} $ is always a Hamilton sequence for all extremal differentials in $\tau $. S. Wu [‘Hamilton sequences for extremal quasiconformal mappings of the unit disk’, Sci. China Ser. A 42 (1999), 1033–1042] gave a positive answer to this problem in the case where 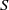$S$ is the unit disc. In this paper, we show that it is also true when 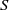$S$ is a doubly-connected domain.

Keywords

Teichmüller spaceHamilton sequence

MSC classification

Secondary: 30C75: Extremal problems for conformal and quasiconformal mappings, other methods 30C62: Quasiconformal mappings in the plane
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 376 - 379
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Gardiner, F. P., ‘Approximation of infinite dimensional Teichmüller space’, Trans. Amer. Math. Soc. 282 (1984), 367–383.Google Scholar
Gardiner, F. P. and Lakic, N., Quasiconformal Teichmüller Theory (American Mathematical Society, Providence, RI, 2000).Google Scholar
Li, Z., ‘Strebel differentials and Hamilton sequences’, Sci. China Ser. A. 44 (2001), 969–979.Google Scholar
Ohtake, H., ‘Lifts of extremal quasiconformal mappings of arbitrary Riemann surfaces’, J. Math. Kyoto Univ. 2 (1982), 191–200.Google Scholar
Wu, S., ‘Hamilton sequences for extremal quasiconformal mappings of the unit disk’, Sci. China Ser. A. 42 (1999), 1033–1042.CrossRefGoogle Scholar