Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T21:32:32.906Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE SUM OF POWERS OF THE DEGREES OF GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  08 March 2013

RENYU XU ,
JIANLIANG WU ,
GUANGHUI WANG  and
XIN ZHANG
RENYU XU
Affiliation:
School of Mathematics, Shandong University, Jinan, 250100, PR China email [email protected]
JIANLIANG WU*
Affiliation:
School of Mathematics, Shandong University, Jinan, 250100, PR China email [email protected]
GUANGHUI WANG
Affiliation:
School of Mathematics, Shandong University, Jinan, 250100, PR China email [email protected]
XIN ZHANG
Affiliation:
Department of Mathematics, Xidian University, Xi’an, 710071, PR China
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For positive integers 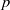$p$ and 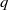$q$, let 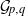${ \mathcal{G} }_{p, q} $ be a class of graphs such that 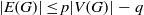$\vert E(G)\vert \leq p\vert V(G)\vert - q$ for every 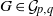$G\in { \mathcal{G} }_{p, q} $. In this paper, we consider the sum of the 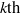$k\mathrm{th} $ powers of the degrees of the vertices of a graph 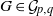$G\in { \mathcal{G} }_{p, q} $ with 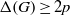$\Delta (G)\geq 2p$. We obtain an upper bound for this sum that is linear in 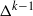${\Delta }^{k- 1} $. These graphs include the planar, 1-planar, $t$-degenerate, outerplanar, and series-parallel graphs.

Keywords

degree sum1-planar graphseries-parallel graphdegenerate graph

MSC classification

Secondary: 05C07: Vertex degrees
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 353 - 358
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Bey, C., ‘An upper bound on the sum of the squares of the degrees in a hypergraph’, Discrete Math. 269 (2003), 259–263.CrossRefGoogle Scholar
de Caen, D., ‘An upper bound on the sum of squares of degrees in a graph’, Discrete Math. 185 (1998), 245–248.CrossRefGoogle Scholar
Fabrici, I. and Madaras, T., ‘The structure of 1-planar graphs’, Discrete Math. 307 (2007), 854–865.CrossRefGoogle Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory with Applications (North-Holland, New York, 1976).CrossRefGoogle Scholar
Harant, J., Jendrol, S. and Madaras, T., ‘Upper bounds on the sum of powers of the degrees of a simple planar graph’, J. Graph Theory 67 (2) (2011), 112–123.Google Scholar
Pach, J. and Tóth, G., ‘Graphs drawn with few crossings per edge’, Combinatorica 17 (3) (1997), 427–439.Google Scholar
Li, J. S. and Pan, Y. L., ‘de Caen’s inequality and bounds on the largest Laplacian eigenvalue of a graph’, Linear Algebra Appl. 328 (2001), 153–160.CrossRefGoogle Scholar
Das, K. Ch., ‘Maximizing the sum of squares of the degrees of a graph’, Discrete Math. 285 (2004), 57–66.CrossRefGoogle Scholar
Cioabǎ, S. M., ‘Sums of powers of the degrees of a graph’, Discrete Math. 306 (2006), 1959–1964.CrossRefGoogle Scholar