Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T21:10:38.108Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE OF ALMOST SPLIT SEQUENCES VIA REGULAR SEQUENCES

Part of: Representation theory of rings and algebras

Published online by Cambridge University Press:  18 March 2013

HOSSEIN ESHRAGHI
HOSSEIN ESHRAGHI*
Affiliation:
Department of Pure Mathematics, Faculty of Mathematical Sciences, University of Kashan, PO Box 87317-51167, Kashan, Iran email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 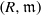$(R, \mathfrak{m})$ be a Cohen–Macaulay complete local ring. We will apply an inductive argument to show that for every nonprojective locally projective maximal Cohen–Macaulay object 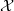$ \mathcal{X} $ of the morphism category of 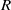$R$ with local endomorphism ring, there exists an almost split sequence ending in 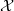$ \mathcal{X} $. Regular sequences are exploited to reduce the Krull dimension of 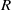$R$ on which the inductive argument is established. Moreover, the Auslander–Reiten translate of certain objects is described.

Keywords

almost split sequenceCohen–Macaulay modulesmorphism category

MSC classification

Secondary: 16G70: Auslander-Reiten sequences (almost split sequences) and Auslander-Reiten quivers 16G50: Cohen-Macaulay modules
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 218 - 231
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Auslander, M., ‘Comments on the functor Ext’, Topology 8 (1969), 151–166.CrossRefGoogle Scholar
Auslander, M., ‘Functors and morphisms determined by objects’, in: Proc. Conf. on Representation Theory (Philadelphia 1967) (Dekker, New York, 1978), 1–244.Google Scholar
Auslander, M. and Reiten, I., ‘Representation theory of Artin algebras III’, Comm. Algebra 3 (1975), 239–294.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., ‘Almost split sequences for Cohen–Macaulay modules’, Math. Ann. 277 (2) (1987), 345–349.CrossRefGoogle Scholar
Auslander, M., Reiten, I. and Smalø, S. O., Representation Theory of Artin Algebras, Cambridge Studies in Advanced Mathematics, 36 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Bruns, W. and Herzog, J., Cohen–Macaulay Rings, Cambridge Studies in Advanced Mathematics, 39 (Cambridge University Press, Cambridge, 1993).Google Scholar
Ding, S. and Solberg, Ø., ‘The Maranda theorem and liftings of modules’, Comm. Algebra 21 (4) (1993), 1161–1187.CrossRefGoogle Scholar
Enochs, E. and Estrada, S., ‘Projective representations of quivers’, Comm. Algebra 33 (2005), 3467–3478.CrossRefGoogle Scholar
Enochs, E., Estrada, S. and García Rozas, J. R., ‘Injective representations of infinite quivers. Applications’, Canad. J. Math. 61 (2) (2009), 315–335.CrossRefGoogle Scholar
Freyd, P., Abelian Categories (Harper & Row, New York, 1964).Google Scholar
Guo, Y., ‘The class of modules with projective cover’, J. Korean Math. Soc. 46 (1) (2009), 51–58.CrossRefGoogle Scholar
Hilton, P. and Rees, D., ‘Natural maps of extension functors and a theorem of R. G. Swan’, Proc. Camb. Phil. Soc. Math. Phys. Sci. 51 (1961).Google Scholar
Leuschke, G. and Wiegand, R., Cohen–Macaulay Representations (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
Miyata, T., ‘Note on direct summands of modules’, J. Math. Kyoto Univ. 7 (1) (1967), 65–69.Google Scholar
Rotman, J. J., An Introduction to Homological Algebra (Academic Press, New York, 1979).Google Scholar
Salarian, Sh. and Vahed, R., Almost split sequences for complexes of maximal Cohen–Macaulay modules, in preparation.Google Scholar
Yoshino, Y., Cohen–Macaulay Modules over Cohen–Macaulay Rings, London Mathematical Society Lecture Note Series, 146 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar