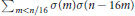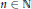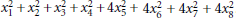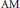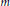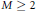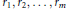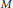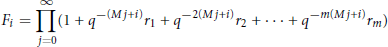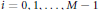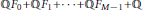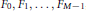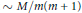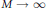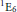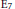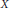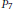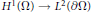Research Article
The Convolution Sum Σm<n/16σ(m)σ(n – 16m)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-14
-
- Article
-
- You have access
- Export citation
The Duality Problem for the Class of AM-Compact Operators on Banach Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 15-20
-
- Article
-
- You have access
- Export citation
A Remark on Extensions of CR Functions from Hyperplanes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-25
-
- Article
-
- You have access
- Export citation
Hinčin's Theorem for Multiplicative Free Convolution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 26-31
-
- Article
-
- You have access
- Export citation
On Linear Independence of a Certain Multivariate Infinite Product
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 32-46
-
- Article
-
- You have access
- Export citation
The Minimal Number of Three-Term Arithmetic Progressions Modulo a Prime Converges to a Limit
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 47-56
-
- Article
-
- You have access
- Export citation
A Note on Integer Symmetric Matrices and Mahler's Measure
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 57-59
-
- Article
-
- You have access
- Export citation
Følner Nets for Semidirect Products of Amenable Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 60-66
-
- Article
-
- You have access
- Export citation
Rearrangement-Invariant Functionals with Applications to Traces on Symmetrically Normed Ideals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 67-80
-
- Article
-
- You have access
- Export citation
Homotopy Formulas for Cyclic Groups Acting on Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-85
-
- Article
-
- You have access
- Export citation
The Numerical Range of 2-Dimensional Krein Space Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 86-99
-
- Article
-
- You have access
- Export citation
Dynamical Zeta Function for Several Strictly Convex Obstacles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 100-113
-
- Article
-
- You have access
- Export citation
Zero Cycles on a Twisted Cayley Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 114-124
-
- Article
-
- You have access
- Export citation
Explicit Real Cubic Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 125-133
-
- Article
-
- You have access
- Export citation
Numerical Semigroups Having a Toms Decomposition
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 134-139
-
- Article
-
- You have access
- Export citation
First Variations of the Best Sobolev Trace Constant with Respect to the Domain
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 140-145
-
- Article
-
- You have access
- Export citation
Stepping-Stone Model with Circular Brownian Migration
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 146-160
-
- Article
-
- You have access
- Export citation