Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T09:48:14.251Z Has data issue: false hasContentIssue false
  • English
  • Français

Følner Nets for Semidirect Products of Amenable Groups

Published online by Cambridge University Press:  20 November 2018

David Janzen
David Janzen*
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 Sherbrooke St. West, Montreal, QC, H3A 2K6 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For unimodular semidirect products of locally compact amenable groups 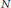$N$ and 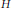$H$, we show that one can always construct a Følner net of the form 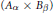$({{A}_{\alpha }}\,\times \,{{B}_{\beta }})$ for $G$, where 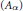$({{A}_{\alpha }})$ is a strong form of Følner net for 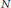$N$ and 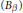$({{B}_{\beta }})$ is any Følner net for 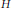$H$. Applications to the Heisenberg and Euclidean motion groups are provided.

Keywords

22D0543A0722D1543A20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 1 , 01 March 2008 , pp. 60 - 66
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Aristov, O., Runde, V., and Spronk, N., Operator biflatness of the Fourier algebra and approximate indicators for subgroups. J. Funct. Anal. 209(2004), no. 2, 367–387.Google Scholar
[2] Greenleaf, F. P., Invariant means on topological groups and their applications. Van Nostrand Mathematical Studies 16, Van Nostrand, New York, 1969.Google Scholar
[3] Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis. I. Structure of Topological Groups. Integration Theory, Group Representations. Grundlehren der MathematischenWissenschaften 115, Springer-Verlag, Berlin, 1963.Google Scholar
[4] Ilie, M. and Spronk, N., Completely bounded homomorphisms of the Fourier algebra. J. Funct. Anal. 225(2005), no. 2, 480–499.Google Scholar
[5] Klawe, M., Semidirect product of semigroups in relation to amenability, cancellation properties, and strong Følner conditions. Pacific J. Math. 73(1977), no. 1, 91–106.Google Scholar
[6] Paterson, A. L. T., Amenability. Mathematical Surveys and Monographs 29, American Mathematical Society, Providence, RI, 1988.Google Scholar
[7] Ruan, Z.-J., The operator amenability of A(G) . Amer. J. Math. 117(1995), no. 6, 1449–1474.Google Scholar
[8] Runde, V., Lectures on Amenability. Lecture Notes in Mathematics 1774, Springer-Verlag, Berlin, 2002.Google Scholar
[9] Stokke, R., Quasi-central bounded approximate identities in group algebras of locally compact groups. Illinois J. Math. 48(2004), no. 1, 151–170.Google Scholar
[10] Stokke, R., Approximate diagonals and Følner conditions for amenable group and semigroup algebras. Studia Math. 164(2004), no. 2, 139–159.Google Scholar
[11] Yang, Z., Følner numbers and Følner type conditions for amenable semigroups. Illinois J. Math. 31(1987), no. 3, 496–517.Google Scholar