Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T10:32:56.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero Cycles on a Twisted Cayley Plane

Published online by Cambridge University Press:  20 November 2018

V. Petrov ,
N. Semenov  and
K. Zainoulline
V. Petrov
Affiliation:
PIMS, University of Alberta, Edmonton, AB, T6G 2G1 e-mail: [email protected]
N. Semenov
Affiliation:
Mathematisches Institut, Universität München, D-80333 München, Germany e-mail: [email protected]@mathematik.uni-muenchen.de
K. Zainoulline
Affiliation:
Mathematisches Institut, Universität München, D-80333 München, Germany e-mail: [email protected]@mathematik.uni-muenchen.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $k$ be a field of characteristic not 2, 3. Let 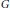$G$ be an exceptional simple algebraic group over $k$ of type 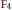${{\text{F}}_{4}},$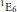$^{1}{{\text{E}}_{6}}$ or 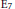${{\text{E}}_{7}}$ with trivial Tits algebras. Let 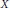$X$ be a projective 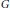$G$-homogeneous variety. If 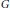$G$ is of type 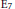${{\text{E}}_{7}},$ we assume in addition that the respective parabolic subgroup is of type 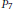${{\text{P}}_{7}}.$ The main result of the paper says that the degree map on the group of zero cycles of 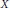$X$ is injective.

Keywords

20G1514C15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 1 , 01 March 2008 , pp. 114 - 124
Copyright
Copyright © Canadian Mathematical Society 2008

References

[Br05] Brosnan, P., On motivic decompositions arising from the method of Białynicki-Birula. Invent. Math. 161(2005), no. 1, 91–111.Google Scholar
[CM] Chernousov, V. and Merkurjev, A., Connectedness of classes of fields and zero-cycles on projective homogeneous varieties. Compos. Math. 142(2006), no. 6, 1522–1548.Google Scholar
[DG] Demazure, M. and Grothendieck, A., eds. Schémas en groupes. III: Structure des schémas en groupes réductifs. Lecture Notes in Mathematics 153, Springer-Verlag, Berlin, 1962/1964.Google Scholar
[Fe72] Ferrar, J. C., Strictly regular elements in Freudenthal triple systems. Trans. Amer. Math. Soc. 174(1972), 313–331.Google Scholar
[Ga01] Garibaldi, R. S., Structurable algebras and groups of type E6 and E7 . J. Algebra 236(2001), no. 2, 651–691.Google Scholar
[IM05] Iliev, A. and Manivel, L., On the Chow ring of the Cayley plane. Compositio Math. 141(2005), no. 1, 146–160.Google Scholar
[Inv] Knus, M.-A., Merkurjev, A., Rost, M., and Tignol, J.-P., The book of involutions. American Mathematical Society Colloquium Publications 44, American Mathematical Society, Providence, RI, 1998.Google Scholar
[Kr05] Krashen, D., Zero cycles on homogeneous varieties. Preprint (2005) arXiv:math.AG/0501399Google Scholar
[Me95] Merkurjev, A.. Zero-dimensional cycles on some involutive varieties. J. Math. Sci. (New York) 89(1998), no. 2, 1141–1148 (translation).Google Scholar
[Me] Merkurjev, A.. Rational correspondences (after Rost, M.). Preprint http://www.math.ucla.edu/_merkurev Google Scholar
[Pa84] Panin, I., Application of K-theory in algebraic geometry. Ph.D. thesis LOMI, Leningrad, 1984.Google Scholar
[PR94] Petersson, H. and Racine, M., Albert algebras. In: Jordan Algebras. de Gruyter, Berlin, 1994, pp. 197–207.Google Scholar
[Po05] Popov, V., Generically multiple transitive algebraic group actions. 2005, http://www.math.uni-bielefeld.de/LAG Google Scholar
[SK77] Sato, M. and Kimura, T., A classification of irreducible prehomogeneous vector spaces and their relative invariants. Nagoya Math. J. 65(1977), 1–155.Google Scholar
[SV] Springer, T. and Veldkamp, F., Octonions, Jordan Algebras and Exceptional Groups. Springer-Verlag, Berlin, 2000.Google Scholar
[SV68] Springer, T. and Veldkamp, F., On Hjelmslev-Moufang planes. Math. Z. 107(1968), 249–263.Google Scholar
[Sw89] Swan, R., Zero cycles on quadric hypersurfaces. Proc. Amer.Math. Soc. 107(1989), no. 1, 43–46.Google Scholar
[Ti66] Tits, J., Classification of algebraic semisimple groups. In: Algebraic Groups and Discontinuous Subgroups. American Mathematical Society, Providence, RI, 1966, pp. 33–62.Google Scholar
[Ti71] Tits, J., Représentations linéaires irréductibles d’un groupe réductif sur un corps quelconque. J. Reine Angew. Math. 247(1971), 196–220.Google Scholar
[Ti86] Tits, J., Unipotent elements and parabolic subgroups of reductive groups. II. In: Algebraic Groups, Lecture Notes in Math. 1271, Springer, Berlin, 1987, pp. 265–284.Google Scholar
[Ti90] Tits, J., Strongly inner anisotropic forms of simple algebraic groups. J. Algebra 131(1990), no. 2, 648–677.Google Scholar
[TW02] Tits, J. and Weiss, R., Moufang Polygons. Springer-Verlag, Berlin, 2002.Google Scholar