Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-12T19:41:26.197Z Has data issue: false hasContentIssue false
  • English
  • Français

On Linear Independence of a Certain Multivariate Infinite Product

Published online by Cambridge University Press:  20 November 2018

Stephen Choi  and
Ping Zhou
Stephen Choi
Affiliation:
Department of Mathematics and Statistics, Simon Fraser University, Burnaby, BC, V5A 1S6 e-mail: [email protected]
Ping Zhou
Affiliation:
Department of Mathematics, Statistics, and Computer Science, St. Francis Xavier University, Antigonish, NS, B2G 2W5 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

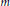Let $q$,$m$,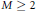$M\,\ge \,2$ be positive integers and 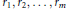${{r}_{1}},\,{{r}_{2}},...,\,{{r}_{m}}$ be positive rationals and consider the following 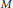$M$ multivariate infinite products

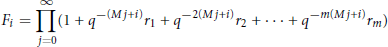$${{F}_{i}}\,=\,\prod\limits_{j=0}^{\infty }{(1\,+\,{{q}^{-(Mj+i)}}\,{{r}_{1}}\,+\,{{q}^{-2(Mj+i)}}\,{{r}_{2}}\,+\,\cdot \cdot \cdot +\,{{q}^{-m(Mj+i)}}\,{{r}_{m}})}$$

for 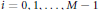$i\,=\,0,\,1,\,.\,.\,.\,,\,M\,-\,1$. In this article, we study the linear independence of these infinite products. In particular, we obtain a lower bound for the dimension of the vector space 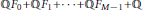$\mathbb{Q}{{F}_{0}}\,+\,\mathbb{Q}{{F}_{1}}\,+\cdot \cdot \cdot +\,\mathbb{Q}{{F}_{M-1}}\,+\,\mathbb{Q}$ over ℚ and show that among these 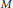$M$ infinite products, 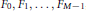${{F}_{0}}\,+\,{{F}_{1}},...,\,{{F}_{M-1}}$ , at least 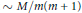$\sim \,M/m\left( m+1 \right)$ of them are irrational for fixed 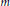$m$ and 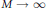$M\,\to \,\infty $.

Keywords

11J72
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 1 , 01 March 2008 , pp. 32 - 46
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Bundschuh, P., Arithmetische Untersuchungen unendlicher Produkte. Invent. Math. 6(1969), 275–295.Google Scholar
[2] Bundschuh, P., Again on the irrationality of a certain infinite product. Analysis 19(1999), no. 1, 93–101.Google Scholar
[3] Bundschuh, P. and Väänänen, K., On the simultaneous Diophantine approximation of new products. Analysis 20(2000), no. 4, 387–393.Google Scholar
[4] Chudnovsky, D. V. and Chudnovsky, G. V., Padé and rational approximation to systems of functions and their arithmetic applications. In: Number Theory. Lecture Notes in Mathematics 1052, Springer-Verlag, Berlin, 1984 pp. 37–84.Google Scholar
[5] Lototsky, A. V., Sur l’irrationalité d’un produit infini. Mat. Sb. 12(54)(1943), 262–272.Google Scholar
[6] Mahler, K., Zur Approximation der Exponentialfunktion und des Logarithmus. J. Reine Angew. Math. 166(1932), 118–150.Google Scholar
[7] Nesterenko, Yu. V., On the linear independence of numbers. (Russian) Vestnik Moskov. Univ. Ser. I Mat. Mekh. 1985 no. 1, 46–49, 108; English translation, Moscow Univ Math. Bull. 40, 69–74.Google Scholar
[8]Yu Popov, A., Arithmetical properties of the values of some infinite products. In: Diophantine Approximations, Moscow, Gos. Univ. 1986, pp. 63–78 (Russian).Google Scholar
[9] Töpfer, T., Arithmetical properties of functions satisfying q-difference equations. Analysis 15(1995), no. 1, 25–49.Google Scholar
[10] Wallisser, R.. Rationale Approximation des q–Analogons der Exponential-funktion und Irrationalitätsaussagen für diese Funktion. Arch. Math. 44(1985), no. 1, 59–64.Google Scholar
[11] Zhou, P., On the irrationality of . Math. Proc. Camb. Phil. Soc. 126(1999), no. 3, 387–397. Erratum. 139(2005), no. 3, 563.Google Scholar
[12] Zhou, P., On the irrationality of a certain multivariate infinite product. Quaest. Math. 29(2006), no. 3, 351–365.Google Scholar
[13] Zhou, P. and Lubinsky, D. S.. On the irrationality of . Analysis 17(1997), 129–153.Google Scholar