Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-24T06:58:24.619Z Has data issue: false hasContentIssue false
  • English
  • Français

Rearrangement-Invariant Functionals with Applications to Traces on Symmetrically Normed Ideals

Published online by Cambridge University Press:  20 November 2018

Nigel Kalton  and
Fyodor Sukochev
Nigel Kalton
Affiliation:
Department of Mathematics, University of Columbia-Missouri, Columbia, MO 65211, U.S.A. e-mail: [email protected]
Fyodor Sukochev
Affiliation:
School of Informatics and Engineering, Flinders University of South Australia, Bedford Park 5042, Australia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

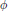We present a construction of singular rearrangement invariant functionals on Marcinkiewicz function/operator spaces. The functionals constructed differ from all previous examples in the literature in that they fail to be symmetric. In other words, the functional $\phi$ fails the condition that if 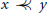$x\prec \prec \,Y$ (Hardy-Littlewood-Polya submajorization) and 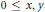$0\,\le \,x,\,y$, then 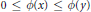$0\,\le \,\phi \left( x \right)\,\le \,\phi \left( y \right)$. We apply our results to singular traces on symmetric operator spaces (in particular on symmetrically-normed ideals of compact operators), answering questions raised by Guido and Isola.

Keywords

46L5247B1046E30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 1 , 01 March 2008 , pp. 67 - 80
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Albeverio, S., Guido, D., Ponosov, A., and Scarlatti, S., Singular traces and compact operators. J. Funct. Anal. 137(1996), no. 2, 281–302.Google Scholar
[2] Braverman, M. and Mekler, A., The Hardy-Littlewood property for symmetric spaces. Sibirsk. Mat. Zh. 18(1977) no. 3, 522–540, 717, (Russian).Google Scholar
[3] Carey, A., Phillips, J., and Sukochev, F., Spectral flow and Dixmier traces. Adv.Math. 173(2003), no. 1, 68–113.Google Scholar
[4] Carey, A. and Sukochev, F., Dixmier traces and some applications in noncommutative geometry. Uspekhi Mat. Nauk 61(2006), no. 6, 45–110 (Russian).Google Scholar
[5] Connes, A., Noncommutative Geometry. Academic Press, San Diego, 1994.Google Scholar
[6] Dixmier, J., Existence de traces non normales, C. R. Acad. Sci. Paris Sér A-B 262(1966), A1107–A1108.Google Scholar
[7] Dodds, P. G., Dodds, T. K., and de Pagter, B., Fully symmetric operator spaces. Integral Equations Operator Theory 15(1992), no. 6, 942–972.Google Scholar
[8] Dodds, P. G., de Pagter, B., Semenov, E., and Sukochev, F., Symmetric functionals and singular traces. Positivity 2(1988), no. 1, 47–75.Google Scholar
[9] Dodds, P. G., de Pagter, B., Sedaev, A., Semenov, E., and Sukochev, F., Singular symmetric functionals. J. Math. Sci. (New York) 124(2004), no. 2, 4867–4885, translation.Google Scholar
[10] Dodds, P. G., de Pagter, B., Sedaev, A., Semenov, E., and Sukochev, F., Singular symmetric functionals and Banach limits with additional invariance properties. Izv. Math. 67(2003), no. 6, 1187–1213.Google Scholar
[11] Dykema, K. J., Figiel, T., Weiss, G., and Wodzicki, M., Commutator structure of operator ideals. Adv. Math. 185(2004), no. 1, 1–79.Google Scholar
[12] Dykema, K. J. and Kalton, N. J., Sums of commutators in ideals and modules of type II factors. Ann. Inst. Fourier (Grenoble) 55(2005), no. 3, 931–971.Google Scholar
[13] Eoff, C. M. and Kalton, N. J., Zeros of entire functions and characteristic determinants. Complex Variables Theory Appl. 14(1990), no. 1–4, 53–63.Google Scholar
[14] Fack, T. and Kosaki, H., Generalised s-numbers of τ-measurable operators. Pacific J. Math. 123(1986), no. 2, 269–300.Google Scholar
[15] Figiel, T. and Kalton, N. J., Symmetric linear functionals on function spaces. In: Function Spaces, Interpolation Theory and Related Topics. de Gruyter, Berlin, 2002, pp. 311–332.Google Scholar
[16] Guido, D. and Isola, T., Singular traces on semifinite von Neumann algebras. J. Funct. Anal. 134(1995), no. 2, 451–485.Google Scholar
[17] Guido, D. and Isola, T., Dimensions and singular traces for spectral triples, with applications to fractals. J. Funct. Anal. 203(2003), no. 2, 362–400.Google Scholar
[18] Gohberg, I. C. and Krein, M. G., Introduction to the theory of non-selfadjoint operators. Translations of Mathematical Monographs 18, American Mathematical Society, Providence, RI, 1969.Google Scholar
[19] Kalton, N. J., Unusual traces on operator ideals. Math. Nachr. 134(1987), 119–130.Google Scholar
[20] Krein, S., Petunin, Y., and Semenov, E., Interpolation of linear operators. Translations of Mathematical Monographs 54, American Mathematical Society, Providence, RI, 1982.Google Scholar
[21] Lord, S., Sedaev, A., and Sukochev, F., Dixmier traces as singular symmetric functionals and applications to measurable operators. J. Funct. Anal. 224(2005), no. 1, 72–106.Google Scholar
[22] Lorentz, G. G.. A contribution to the theory of divergent sequences. Acta. Math. 80(1948), 167–190.Google Scholar
[23] Lindenstrauss, J. and Tzafriri, L., Classical Banach Space I. Sequence Spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete 92, Springer-Verlag, Berlin, 1977.Google Scholar
[24] Lindenstrauss, J. and Tzafriri, L., Classical Banach Space II. Function Spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete 97, Springer-Verlag, Berlin, 1979.Google Scholar
[25] Russu, G., Symmetric spaces of functions that do not have the majorization property. Mat. Issled. 4(1969), 82–93 (Russian).Google Scholar
[26] Ryff, J. V., Extreme points of some convex subsets of L 1(0, 1) . Proc. Amer. Math. Soc. 18(1967), 1026–1034.Google Scholar
[27] Sucheston, L., Banach limits. Amer. Math. Monthly 74(1967), 308–311.Google Scholar
[28] Varga, J. V., Traces on irregular ideals. Proc. Amer. Math. Soc. 107(1989), no. 3, 715–723.Google Scholar