A Remark on Extensions of CR Functions from Hyperplanes

Abstract

In the characterization of the range of the Radon transform, one encounters the problem of the holomorphic extension of functions defined on 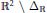${{\mathbb{R}}^{2}}\backslash \,{{\Delta }_{\mathbb{R}}}$ (where 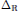${{\Delta }_{\mathbb{R}}}$ is the diagonal in 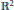${{\mathbb{R}}^{2}}$ ) and which extend as “separately holomorphic” functions of their two arguments. 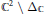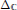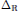In particular, these functions extend in fact to ${{\mathbb{C}}^{2}}\,\backslash \,{{\Delta }_{\mathbb{C}}}$ where ${{\Delta }_{\mathbb{C}}}$ is the complexification of ${{\Delta }_{\mathbb{R}}}$ . We take this theorem from the integral geometry and put it in the more natural context of the 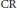$\text{CR}$ geometry where it accepts an easier proof and amore general statement. In this new setting it becomes a variant of the celebrated “edge of the wedge” theorem of Ajrapetyan and Henkin.