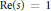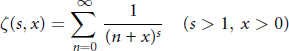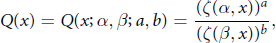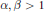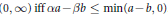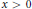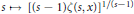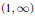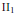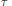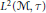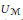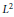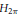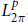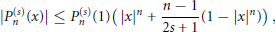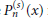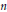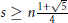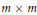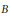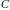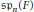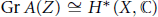Research Article
On Non-Vanishing of Convolution of Dirichlet Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-332
-
- Article
-
- You have access
- Export citation
Monotonicity Properties of the Hurwitz Zeta Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 333-339
-
- Article
-
- You have access
- Export citation
Short Geodesics of Unitaries in the L2 Metric
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 340-354
-
- Article
-
- You have access
- Export citation
On Maps Preserving Products
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 355-369
-
- Article
-
- You have access
- Export citation
Trigonometric Multipliers on H2π
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 370-381
-
- Article
-
- You have access
- Export citation
Uniform Estimates of Ultraspherical Polynomials of Large Order
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 382-393
-
- Article
-
- You have access
- Export citation
Diagonal Plus Tridiagonal Representatives for Symplectic Congruence Classes of Symmetric Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 394-404
-
- Article
-
- You have access
- Export citation
Liouville's Theorem in the Radially Symmetric Case
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 405-408
-
- Article
-
- You have access
- Export citation
The Existence of Universal Inner Functions on the Unit Ball of ℂn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 409-413
-
- Article
-
- You have access
- Export citation
Vector Fields and the Cohomology Ring of Toric Varieties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 414-427
-
- Article
-
- You have access
- Export citation
Reduction of Elliptic Curves in Equal Characteristic 3 (and 2)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 428-444
-
- Article
-
- You have access
- Export citation
On the Garsia Lie Idempotent
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 445-454
-
- Article
-
- You have access
- Export citation
On Gâteaux Differentiability of Convex Functions in WCG Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 455-459
-
- Article
-
- You have access
- Export citation
B-Stable Ideals in the Nilradical of a Borel Subalgebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 460-472
-
- Article
-
- You have access
- Export citation
Logarithms and the Topology of the Complement of a Hypersurface
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 473-480
-
- Article
-
- You have access
- Export citation