Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T17:57:15.057Z Has data issue: false hasContentIssue false
  • English
  • Français

On Gâteaux Differentiability of Convex Functions in WCG Spaces

Published online by Cambridge University Press:  20 November 2018

Jan Rychtář
Jan Rychtář*
Affiliation:
Department of Mathematical Sciences, University of North Carolina at Greensboro, Greensboro, NC 27402, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown, using the Borwein–Preiss variational principle that for every continuous convex function 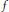$f$ on a weakly compactly generated space 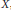$X$, every 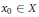${{x}_{0}}\in X$ and every weakly compact convex symmetric set 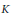$K$ such that 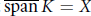$\overline{\text{span}}K=X$, there is a point of Gâteaux differentiability of 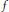$f$ in 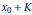${{x}_{0}}+K$. This extends a Klee's result for separable spaces.

Keywords

46B20Gâteaux smoothnessBorwein–Preiss variational principleweakly compactly generated spaces
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 3 , 01 September 2005 , pp. 455 - 459
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Borwein, J. and Preiss, D., A smooth variational principle with applications to subdifferentiability and differentiability of convex functions. Trans. Am. Math. Soc. 303(1987), 517–527.Google Scholar
[2] Deville, R., Godefroy, G., and Zizler, V., Smoothness and renormings in Banach spaces. Pitman Monographs and Surveys in Pure and Applied Mathematics 64, Wiley, New York, 1993.Google Scholar
[3] Fabian, M., Gâteaux differentiability of convex functions and topology. Weak Asplund spaces. Canadian Mathematical Society Series of Monographs and Advanced Texts. John Wiley and Sons, New York, 1997 Google Scholar
[4] Fabian, M., Habala, P., Hájek, P., Santalucia, V. Montesinos, Pelant, J., and Zizler, V.. Functional analysis and infinite-dimensional geometry. CMS Books in Mathematics 8, Springer-Verlag, New York, 2001.Google Scholar
[5] Klee, V., Some new results on smoothness and rotundity in normed linear spaces. Math. Ann. 139(1959), 51–63.Google Scholar
[6] Phelps, R. R., Convex functions, monotone operators and differentiability. Second edition, Lecture Notes in Mathematics 1364, Springer-Verlag, Berlin, 1993.Google Scholar