Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T17:52:22.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotonicity Properties of the Hurwitz Zeta Function

Published online by Cambridge University Press:  20 November 2018

Horst Alzer
Horst Alzer*
Affiliation:
Morsbacher Str. 10, D-51545 Waldbröl, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let

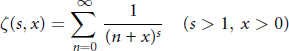$$\zeta \left( s,x \right)=\sum\limits_{n=0}^{\infty }{\frac{1}{{{\left( n+x \right)}^{s}}}}\left( s>1,x>0 \right)$$

be the Hurwitz zeta function and let

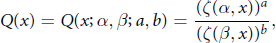$$Q\left( x \right)=Q\left( x;\alpha ,\beta ;a,b \right)=\frac{{{\left( \zeta \left( \alpha ,x \right) \right)}^{a}}}{{{\left( \zeta \left( \beta ,x \right) \right)}^{{{b}'}}}}$$

where 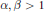$\alpha ,\beta >1$ and 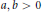$a,b>0$ are real numbers. We prove: (i) The function 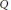$Q$ is decreasing on 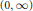$\left( 0,\infty \right)$ iff 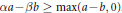$\alpha a-\beta b\ge \max \left( a-b,0 \right)$. (ii) 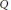$Q$ is increasing on 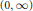$\left( 0,\infty \right)$ iff 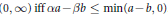$\alpha a-\beta b\le \min \left( a-b,0 \right)$. An application of part (i) reveals that for all 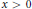$x>0$ the function 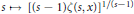$s\mapsto {{\left[ \left( s-1 \right)\zeta \left( s,x \right) \right]}^{1/\left( s-1 \right)}}$ is decreasing on 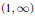$\left( 1,\infty \right)$. This settles a conjecture of Bastien and Rogalski.

Keywords

11M3526D15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 3 , 01 September 2005 , pp. 333 - 339
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Alzer, H., Inequalities for the Hurwitz zeta function. Proc. Roy. Soc. Edinburgh Sect. A 130(2000), 1227–1236.Google Scholar
[2] Andrews, G. E., Askey, R., and Roy, R., Special Functions. Encyclopedia of Mathematics and its Applications 71, Cambridge University Press, Cambridge, 1999.Google Scholar
[3] Apostol, T. M., Introduction to Analytic Number Theory. Springer-Verlag, New York, 1976.Google Scholar
[4] Bastien, G. and Rogalski, M., Convexité, complète monotonie et inégalités sur les fonctions zêta et gamma, sur les fonctions des opérateurs de Baskakov et sur des fonctions arithmétiques. Canad. J. Math. 54(2002), 916–944.Google Scholar
[5] Lippert, R. A., A probabilistic interpretation of the Hurwitz zeta function. Adv. Math. 97(1993), 278–284.Google Scholar
[6] Trimble, S. Y., Wells, J., and Wright, F. T., Superadditive functions and a statistical application. SIAM J. Math. Anal. 20(1989), 1255–1259.Google Scholar
[7] Zhang, N.-Y. and Williams, K. S., Some results on the generalized Stieltjes constants. Analysis 14(1994), 147–162.Google Scholar