Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T17:57:13.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform Estimates of Ultraspherical Polynomials of Large Order

Published online by Cambridge University Press:  20 November 2018

Laura De Carli
Laura De Carli*
Affiliation:
Department of Mathematics, Florida International University, University Park, Miami, FL 33199, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove the sharp inequality

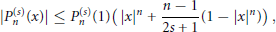$$\left| P_{n}^{\left( s \right)}\left( x \right) \right|\le P_{n}^{\left( s \right)}\left( 1 \right)\left( {{\left| x \right|}^{n}}+\frac{n-1}{2s+1}\left( 1-{{\left| x \right|}^{n}} \right) \right)$$

where 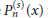$P_{n}^{\left( s \right)}\left( x \right)$ is the classical ultraspherical polynomial of degree 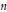$n$ and order 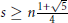$s\ge n\frac{1+\sqrt{5}}{4}$. This inequality can be refined in 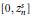$\left[ 0,z_{n}^{s} \right]$ and 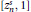$\left[ z_{n}^{s},1 \right]$, where 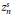$z_{n}^{s}$ denotes the largest zero of 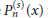$P_{n}^{\left( s \right)}\left( x \right)$.

Keywords

42C0533C47
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 3 , 01 September 2005 , pp. 382 - 393
Copyright
Copyright © Canadian Mathematical Society 2005

References

[AAR] Andrews, G. E., Askey, R., and Roy, R.. Special functions. Encyclopedia of Mathematics and its Applications, Vol. 71. Cambridge University Press, Cambridge, 1999.Google Scholar
[ADGR] Area, I., Dimitrov, D. K., Godoy, E., and Ronveaux, A., Zeros of Gegenbauer and Hermite polynomials and connection coefficients. Math. Comp. 73(2004), 1937–1951.Google Scholar
[E] Elbert, A., Some recent results on the zeros of Bessel functions and orthogonal polynomials. J. Comput. Appl. Math. 133(2001), 65–83.Google Scholar
[EL1] Elbert, A., and Laforgia, A., Upper bounds for the zeros of ultraspherical polynomials. J. Approx. Theory 61(1990), 88–97.Google Scholar
[EL2] Elbert, A., and Laforgia, A., Asymptotic formulas for ultraspherical polynomials and their zeros for large value of λ. Proc. Amer. Math. Soc. 114(1992), 371–377.Google Scholar
[EMO] Erdélyi, A., Magnus, W., Oberhettinger, F., and Tricomi, F. G., Tables of integral transforms, Vol. 2, McGraw-Hill, 1954.Google Scholar
[IS1] Ifantis, E. K., and Siafarikas, P. D., A differential inequality for the zeros of Bessel functions. Applicable Anal. 20(1985), 269–281.Google Scholar
[IS2] Ifantis, E. K., and Siafarikas, P. D., Differential inequality for the positive zeros of Bessel functions. J. Comput. Appl. Math. 30(1990), 139–143.Google Scholar
[I] Ismail, M. E. H., Monotonicity of zeros of orthogonal polynomials. Springer, New York, 1989, pp. 177–190.Google Scholar
[Sz] Szegő, G., Orthogonal polinomials. American Mathematical Society Colloquium Publications Vol. 23, American Mathematical Society, Providence, RI, 1939.Google Scholar