Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-20T18:26:56.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Logarithms and the Topology of the Complement of a Hypersurface

Published online by Cambridge University Press:  20 November 2018

E. S. Zeron
E. S. Zeron*
Affiliation:
Departamento de Matemáticas, Cinvestav, Apartado Postal 14-740, México DF, 07000, México e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is devoted to analysing the relation between the logarithm of a non-constant holomorphic polynomial 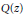$Q\left( z \right)$ and the topology of the complement of the hypersurface defined by 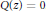$Q\left( z \right)=0$.

Keywords

32Q5514F45Logarithmhomology groups and periods
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 3 , 01 September 2005 , pp. 473 - 480
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Bredon, G. E., Topology and Geometry. Graduate Texts in Mathematics 139, Springer-Verlag, New York, 1993.Google Scholar
[2] Broughton, S. A., On the topology of polynomial hypersurfaces. In: Singularities, Proc. Sympos. Pure Math. 40, Part I, American Mathematical Society, Providence, RI, 1983, pp. 167–178.Google Scholar
[3] Dimca, A., Singularities and Topology of Hypersurfaces. Springer-Verlag, New York, 1992.Google Scholar
[4] Dodson, C. T. J. and Parker, P. E., A user's guide to algebraic topology. Mathematics and its Applications 387, Kluwer Academic Publishers, Dordrecht, 1997.Google Scholar
[5] Griffiths, P. A., On the periods of certain rational integrals. I. Ann. of Math. (2) 90(1969), pp. 460–495.Google Scholar
[6] Griffiths, P. A., On the periods of certain rational integrals. II. Ann. of Math. (2) 90(1969), pp. 496–541.Google Scholar
[7] Hall, M. Jr., The Theory of Groups. Chelsea Publishing, New York, 1976.Google Scholar
[8] Vui, Há Huy and Tráng, Lê Dũng, Sur la topologie des polynômes complexes. Acta Math. Vietnam. 9(1984), pp. 21–32.Google Scholar
[9] Nemirovskiĭ, S. Yu., Topology of hypersurface complements in C n and rationally convex hulls. Tr. Mat. Inst. Steklova 235(2001), pp. 169–180. English translation in Proc. Steklov Inst.Math. 235(2001), pp. 162–172.Google Scholar
[10] Poincaré, H., Sur les résidues des intégrales doubles. Acta Math. 9(1887), pp. 321–380.Google Scholar
[11] Sklyarenko, E. G., Homology and cohomology theories of general spaces. General topology, II, Encyclopaedia Math. Sci. 50, Springer, Berlin, 1996, pp. 119–256.Google Scholar
[12] Spanier, E. H., Algebraic topology, McGraw-Hill, New York, 1966.Google Scholar
[13] Verdier, J. L., Stratifications de Whitney et théorème de Bertini-Sard, Invent. Math. 36(1976), pp. 295–312.Google Scholar