Article contents
On the Garsia Lie Idempotent
Published online by Cambridge University Press: 20 November 2018
Abstract
The orthogonal projection of the free associative algebra onto the free Lie algebra is afforded by an idempotent in the rational group algebra of the symmetric group 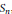 ${{S}_{n}}$, in each homogenous degree
${{S}_{n}}$, in each homogenous degree  $n$. We give various characterizations of this Lie idempotent and show that it is uniquely determined by a certain unit in the group algebra of
$n$. We give various characterizations of this Lie idempotent and show that it is uniquely determined by a certain unit in the group algebra of 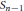 ${{S}_{n-1}}$. The inverse of this unit, or, equivalently, the Gram matrix of the orthogonal projection, is described explicitly. We also show that the Garsia Lie idempotent is not constant on descent classes (in fact, not even on coplactic classes) in
${{S}_{n-1}}$. The inverse of this unit, or, equivalently, the Gram matrix of the orthogonal projection, is described explicitly. We also show that the Garsia Lie idempotent is not constant on descent classes (in fact, not even on coplactic classes) in 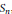 ${{S}_{n}}$.
${{S}_{n}}$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2005
References
- 3
- Cited by


