Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-19T16:47:35.694Z Has data issue: false hasContentIssue false
  • English
  • Français

Short Geodesics of Unitaries in the L2 Metric

Published online by Cambridge University Press:  20 November 2018

Esteban Andruchow
Esteban Andruchow*
Affiliation:
Instituto de Ciencias Universidad Nacional de Gral. Sarmiento, J. M. Gutierrez entre J.L. Suarez y Verdi, (1613) Los Polvorines, Argentina e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

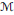Let $\mathcal{M}$ be a type 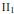$\text{I}{{\text{I}}_{1}}$ von Neumann algebra, 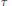$\tau$ a trace in 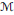$\mathcal{M}$, and 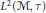${{L}^{2}}\left( \mathcal{M},\tau \right)$ the GNS Hilbert space of 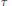$\tau$. We regard the unitary group 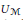${{U}_{\mathcal{M}}}$ as a subset of 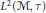${{L}^{2}}\left( \mathcal{M},\tau \right)$ and characterize the shortest smooth curves joining two fixed unitaries in the 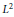${{L}^{2}}$ metric. As a consequence of this we obtain that 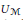${{U}_{\mathcal{M}}}$, though a complete (metric) topological group, is not an embedded riemannian submanifold of 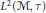${{L}^{2}}\left( \mathcal{M},\tau \right)$

Keywords

46L5158B1058B25unitary groupshort geodesicsinfinite dimensional riemannian manifolds
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 3 , 01 September 2005 , pp. 340 - 354
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Andruchow, E., A non smooth exponential. Studia Math. 155(2003), 265–271.Google Scholar
[2] Atkin, C. J., The Finsler geometry of groups of isometries of Hilbert space. J. Austral. Math. Soc. Ser. A 42(1987), 196–222.Google Scholar
[3] Christensen, E., Universally bounded operators on von Neumann algebras of type II1 . In: Algebraic methods in operator theory, Birkäuser Boston, Boston, MA, 1994, 195–204.Google Scholar
[4] Durán, C. E., Mata-Lorenzo, L. E., and Recht, L., Natural variational problems in the Grassmann manifold of a C*-algebra with trace. Adv. Math. 154(2000), 196–228.Google Scholar
[5] Mata-Lorenzo, L. and Recht, L., Convexity properties of Tr[(a* a)n]. Linear Algebra Appl. 315(2000), 25–38.Google Scholar
[6] Michael, E., Convex structures and continuous selections. Canadian J. Math. 11(1959), 556–575.Google Scholar
[7] Popa, S. and Takesaki, M., The topological structure of the unitary and automorphism groups of a factor. Commun. Math. Phys. 155(1993), 93–101.Google Scholar
[8] Read, M. and Simon, B., Methods of Modern Mathematical Physics, I: Functional Analysis. 2nd ed. Academic Press, New York, 1980.Google Scholar
[9] Segal, I. E., A non commutative extension of abstract integration. Ann. of Math. 57(1953), 401–457.Google Scholar
[10] Takesaki, M., Theory of Operator Algebras. I. Springer-Verlag, New York, 1979.Google Scholar