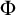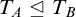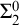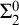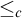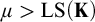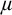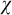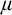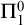Article
THE TURING DEGREES AND KEISLER’S ORDER
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2022, pp. 331-341
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REMARKS ON CONVERGENCE OF MORLEY SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2023, pp. 1339-1357
-
- Article
-
- You have access
- HTML
- Export citation
POLISH SPACE PARTITION PRINCIPLES AND THE HALPERN–LÄUCHLI THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 19 January 2024, pp. 1798-1816
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON COHEN AND PRIKRY FORCING NOTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 September 2023, pp. 858-904
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INFINITARY LOGIC HAS NO EXPRESSIVE EFFICIENCY OVER FINITARY LOGIC
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1817-1834
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLYHEDRAL COMPLETENESS OF INTERMEDIATE LOGICS: THE NERVE CRITERION
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2022, pp. 342-382
-
- Article
-
- You have access
- HTML
- Export citation
ON CUPPING AND AHMAD PAIRS
- Part of:
-
- Published online by Cambridge University Press:
- 12 December 2022, pp. 1358-1369
-
- Article
-
- You have access
- HTML
- Export citation
KEISLER’S THEOREM AND CARDINAL INVARIANTS
-
- Published online by Cambridge University Press:
- 18 November 2022, pp. 905-917
-
- Article
-
- You have access
- HTML
- Export citation
COMPUTABLE VS DESCRIPTIVE COMBINATORICS OF LOCAL PROBLEMS ON TREES
- Part of:
-
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1835-1849
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INVESTIGATING THE COMPUTABLE FRIEDMAN–STANLEY JUMP
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2023, pp. 918-944
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STABILITY RESULTS ASSUMING TAMENESS, MONSTER MODEL, AND CONTINUITY OF NONSPLITTING
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2023, pp. 383-425
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE C.E. DEGREES REALIZABLE IN
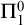 $\Pi ^0_1$ CLASSES
$\Pi ^0_1$ CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1370-1395
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
JSL volume 89 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 27 January 2025, pp. f1-f3
-
- Article
-
- You have access
- Export citation
JSL volume 89 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 21 May 2024, pp. f1-f3
-
- Article
-
- You have access
- Export citation
JSL volume 89 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 April 2024, pp. f1-f3
-
- Article
-
- You have access
- Export citation
JSL volume 89 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 November 2024, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JSL volume 89 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 April 2024, pp. b1-b5
-
- Article
-
- You have access
- Export citation
JSL volume 89 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 November 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation
JSL volume 89 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 21 May 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation
JSL volume 89 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 27 January 2025, pp. b1-b10
-
- Article
-
- You have access
- Export citation