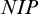REMARKS ON CONVERGENCE OF MORLEY SEQUENCES

Abstract

We refine results of Gannon [6, Theorem 4.7] and Simon [22, Lemma 2.8] on convergence of Morley sequences. We then introduce the notion of eventual$NIP$, as a property of a model, and prove a variant of [15, Corollary 2.2]. Finally, we give new characterizations of generically stable types (for countable theories) and reinforce the main result of Pillay [17] on the model-theoretic meaning of Grothendieck’s double limit theorem.

1 Introduction

Pillay and Tanović [18] introduced the notion of generically stable type, for arbitrary theories, as an abstraction of the crucial properties of definable types in stable theories. All invariant types in $NIP$ theories and all generically stable types in arbitrary theories share an important phenomenon: convergence of Morley sequences. Using this phenomenon/property, although it is not explicitly mentioned, Simon [22] proved the following interesting result:

Simon’s lemma ¹ : Let T be a countable $NIP$ theory and M a countable model of T. Suppose that $p(x)\in S(\cal U)$ is finitely satisfiable in M. Then there is a sequence $(c_i)$ in M such that $\lim tp(c_i/{\cal U})=p$ .

The present paper aims to focus on convergence of Morley sequences. The core of our observations/proofs here is that the convergence of tuples/types depends on a certain type of formulas, namely symmetric formulas. We show that a sequence of types converges if and only if there are some symmetric formulas that are not true in the sequence.

On the other hand, the origin of Simon’s lemma is related to the following crucial theorem in functional analysis due to Bourgain, Fremlin, and Talagrand [3, Theorem 3F]:

BFT theorem: Let X be a Polish space. Then the space $B_1(X)$ of all Baire 1 functions on X is an angelic space with the topology of pointwise convergence.

In [13, Appendix A], it is shown that complete types (not just $\phi $ -types) can be coded by suitable functions, and a refinement of Simon’s lemma is given using the BFT theorem. Recall that every point in the closure of a relatively compact set of an angelic space is the limit of a sequence of its points, and relatively compact sets of $B_1(X)$ possess a property similar to $NIP$ (cf. [16]). In this paper we aim to give a model theoretic version of the Bourgain–Fremlin–Talagrand result in the terms of convergent Morley sequences. ² More precisely, we prove that:

Theorem A: Let T be a countable theory and M a countable model of T. ³

(1) Suppose that $p(x)\in S(\cal U)$ is finitely satisfiable in M and there is a Morley sequence $(d_i)$ of p over M such that $(tp(d_i/{\cal U}):i<\omega )$ converges. Then there is a sequence $(c_i)\in M$ such that $\lim tp(c_i/{\cal U})=p$ .

(2) Furthermore, the following are equivalent:

(i) M is eventually $NIP$ (as in Definition 3.1).

(ii) For any $p(x)\in S(\cal U)$ which is finitely satisfiable in M, there is a sequence $(c_i)\in M$ such that the sequence $(tp(c_i/{\cal U}):i<\omega ) DBSC$ -converges to p (as in Definition 3.4).

(iii) For any $p(x)\in S(\cal U)$ which is finitely satisfiable in M, there is a Morley sequence $(d_i)$ of p over M such that $(tp(d_i/{\cal U}):i<\omega )$ converges.

Recall that Morley sequences in $NIP$ theories are convergent (cf. Definition 2.9). ⁴ Therefore, as the theory T in Theorem A is arbitrary, the equivalences (i)–(iii) of Theorem A(2) refine Simon’s lemma. On the other hand, a result of Gannon [6, Theorem 4.7] asserts that:

Gannon’s theorem: Let T be a countable theory and M a (not necessarily countable) model of T. Suppose that $p(x)\in S(\cal U)$ is generically stable over M. Then there is a sequence $(c_i)$ in M such that $\lim tp(c_i/{\cal U})=p$ .

This follows from Theorem A(1) and the fact that every generically stable type over M is generically stable over a countable elementary substructure of M. We also give a refinement of Gannon’s theorem. In fact, we give a new characterization of generically stable types for countable theories:

Theorem B: Let T be a countable theory, M a model of T, and $p(x)\in S({\cal U})$ a global M-invariant type. The following are equivalent:

(i) p is generically stable over M.

(ii) p is definable over M, AND there is a sequence $(c_i)$ in M such that $(tp(c_i/{\cal U}):i<\omega ) DBSC$ -converges to p (as in Definition 3.4).

Suppose moreover that T has $NSOP$ , then (iii) below is also equivalent to (i) and (ii) above:

(iii) There is a sequence $(c_i)$ in M such that $(tp(c_i/{\cal U}):i<\omega ) DBSC$ -converges to p.

Notice that, as $DBSC$ -convergence is strictly stronger than usual convergence, Theorem B is a clear refinement of Gannon’s theorem. Moreover, this result can be lead to an answer to [6, Question 4.15].

Theorems A and B allow us to reinforce the main result of [17] on generic stability in a model. That is,

Theorem C: Let T be a (countable or uncountable) theory, and let M be a model of T. The following are equivalent:

(i) Any type $p\in S_x(M)$ has an extension to a global type $p'\in S_x({\cal U})$ which is generically stable over M.

(ii) M has no order (as in Definition 4.8) AND M is eventually $NIP$ .

It is worth mentioning that Gannon’s theorem based on the idea of Simon’s lemma, and our results/observations are based on ideas of both of them. This paper is a kind of companion-piece to [16] and [9], although here we are mainly concerned with model-theoretic proofs of variants of results from [16].

This paper is organized as follows. In Section 2, we fix some model theoretic conventions. We will also prove Theorem A(1) (cf. Theorem 2.11) In Section 3, we will provide all necessary functional analysis notions, and introduce the notion of eventual $NIP$ . We will also prove Theorem A(2) (cf. Theorem 3.6) In Section 4, we will study generically stable types in arbitrary/countable theories. We will also prove Theorem B and Theorem C (cf. Theorems 4.4 and 4.10) At the end paper we conclude some remarks/questions on future generalizations and applications of the results/observations.

2 Convergent Morley sequences

The notation is standard, and a text such as [21] will be sufficient background. We fix a first-order language L, a complete countable L-theory T (not necessarily $NIP$ ), and a countable model M of T. The monster model is denoted by $\cal U$ and the space of global types in the variable x is denoted by $S_x({\cal U})$ or $S({\cal U})$ .

Convention 2.1. In this paper, when we say that $(a_i)\subset {\cal U}$ is a sequence, we mean the usual notion in the sense of analysis. That is, every sequence is indexed by $\omega $ . Similarly, we consider Morley sequences indexed by $\omega $ .

Convention 2.2. In this paper, a variable x is a tuple of length n (for $n<\omega $ ). ⁵ Sometimes we write $\bar x$ or $x_1,\ldots ,x_n$ instead of x. All types are n-type (for $n<\omega $ ) unless explicitly stated otherwise. Similarly, a sequence $(a_i)\subset {\cal U}$ is a sequence of tuples of length n (for $n<\omega $ ).

Convention 2.3. In this paper, when we say that $\phi $ is a formula, we mean a formula over $\emptyset $ . Otherwise, we explicitly say that $\phi $ is an $L(A)$ -formula for some set/model A. Although the structure of some important definitions and proofs does not depend on the parameter at all.

Definition 2.4. Let $A\subset \cal U$ and $\phi (x_1,\ldots ,x_n)\in L(A)$ . We say that $\phi (x_1,\ldots ,x_n)$ is symmetric if for any permutation $\sigma $ of $\{1,\ldots ,n\}$ ,

$$\begin{align*}\models\forall\bar x\big(\phi(x_1,\ldots,x_n)\leftrightarrow\phi(x_{\sigma{(1)}},\ldots,x_{\sigma{(n)}})\big).\end{align*}$$

For a formula $\phi (x)$ (with or without parameters) and a sequence $(a_i)$ of x-tuples in $\cal U$ , we write $\lim _{i\to \infty }\phi (a_i)=1$ if there is a natural number n such that ${\cal U}\models \phi (a_i)$ for all $i\geq n$ . If $\lim _{i\to \infty }\neg \phi (a_i)=1$ we write $\lim _{i\to \infty }\phi (a_i)=0$ .

For a formula $\phi (x_{i_0},\ldots ,x_{i_k})$ and a sequence $(b_i)\in \cal U$ , if there exists an $n_\phi $ such that for any $i_k>\cdots >i_0>n_\phi $ we have ${\cal U}\models \phi (b_{i_0},\ldots ,b_{i_k})$ , we write $\lim _{i_0<\cdots <i_k, \ i_0\to \infty } \phi (b_{i_0},\ldots ,b_{i_k})=1$ .

Definition 2.5. (i) Let $(b_i)$ be a sequence of elements in $\cal U$ and $A\subset \cal U$ a set. The eventual Ehrenfeucht–Mostovski type ⁶ (abbreviated $EEM$ -type) of $(b_i)$ over A, which is denoted by $EEM((b_i)/A)$ , is the following (partial) type in $S_\omega (A)$ :

$$\begin{align*}\phi(x_0,\ldots,x_k)\in EEM((b_i)/A) \iff \lim_{i_0<\cdots<i_k, \ i_0\to\infty} \phi(b_{i_0},\ldots,b_{i_k})=1.\end{align*}$$

(ii) Let $(b_i)$ be a sequence of $\cal U$ and $A\subset \cal U$ a set. The symmetric eventual Ehrenfeucht–Mostovski type (abbreviated $SEEM$ -type) of $(b_i)$ over A, which is denoted by $SEEM((b_i)/A)$ , is the following partial type in $S_\omega (A)$ :

$$\begin{align*}\big\{\phi=\phi(x_0,\ldots,x_n):\phi\in EEM((b_i)/A) \text{ and }\phi \text{ is symmetric} \big\}.\end{align*}$$

Whenever $(b_i)$ is A-indiscernible, we sometimes write $SEM((b_i)/A)$ instead of $SEEM((b_i)/A)$ .

(iii) Let $p(x)$ be a type in $S_\omega (A)$ (or $S_\omega ({\cal U})$ ). The symmetric type of p, denoted by Sym $(p)$ , is the following partial type:

$$\begin{align*}\big\{\phi(x)\in p: \phi \text{ is symmetric} \big\}.\end{align*}$$

The sequence $(b_i)$ is called eventually indiscernible over A if $EEM((b_i)/A)$ is a complete type. In this case, for any $L(A)$ -formula $\phi (x)$ , the limit $\lim _{i\to \infty }\phi (b_i)$ is well-defined.

Fact 2.6 [6, Fact 4.2].

Let $ (b_i)$ be a sequence of elements in $\cal U$ and $A\subset \cal U$ such that $|A| = \aleph _0$ . Then there exists a subsequence $(c_i)$ of $ (b_i)$ such that $(c_i)$ is eventually indiscernible over A.

Proof A generalization of this observation (for continuous logic) is proved in Proposition 5.3 of [6].

Let A be a set/model and $p(x)$ a global A-invariant type. The Morley type (or sequence) of $p(x)$ is denoted by $p^{(\omega )}$ (cf. [21, Section 2.2.1]) The restriction of $p(x)$ to A is denoted by $p|_{A}$ . A realisation $(d_i:i<\omega )$ of $p^{(\omega )}|_A$ is called a Morley sequence of/in p over A.

Lemma 2.7. Let $p(x)\in S(\cal U)$ be invariant over A, and $I=(d_i)$ a Morley sequence in p over A.

(i) If there is a sequence $(c_i)\in A$ such that $\lim tp(c_i/AI)=p|_{AI}$ and $(c_i)$ is eventually indiscernible over $AI$ , then $SEEM((c_i)/A)=\text {Sym}(p^{(\omega )}|_A)$ .

(ii) If p is finitely satisfiable in A and $|A|=\aleph _0$ , then there is a sequence $(c_i)$ in A such that $\lim tp(c_i/AI)=p|_{AI}$ and $(c_i)$ is eventually indiscernible over $AI$ . Therefore, $SEEM((c_i)/A)=\text {Sym}(p^{(\omega )}|_A)$ .

Proof (i): Suppose that there is a sequence $(c_i)$ such that $\lim tp(c_i/AI)=p|_{AI}$ and $(c_i)$ is eventually indiscernible over $AI (\dagger )$ . Set $J=(c_i)$ .

We show that $SEEM((c_i)/A)=SEM((d_i)/A)=\text {Sym}(p^{(\omega )}|_A)$ . We remind the reader that $SEM((d_i)/A)=\text {Sym}(p^{(\omega )}|_A)$ follows from the definition of a Morley sequence. The proof is by induction on symmetric formulas. The base case works. Indeed, for any $L(A)$ -formula $\phi (x_0)$ , $\phi (x_0)\in SEEM((c_i)/A)\iff \lim \phi (c_i)=1\iff \phi (x_0)\in p\iff \phi (x_0)\in SEM((d_i)/A)$ .

The induction hypothesis is that for any symmetric formula $\phi (x_0,\ldots ,x_{k-1})$ in $L(A)$ , $\phi (x_0,\ldots ,x_{k-1})\in SEEM((c_i)/A)$ if and only if $\phi (x_0,\ldots ,x_{k-1})\in SEM((d_i)/A)$ .

Let $\phi (x_0,\ldots ,x_{k})$ be a symmetric $L(A)$ -formula $(\ddagger )$ . Clearly, for any $c\in A$ , the $L(A)$ -formula $\phi (c,x_1,\ldots ,x_{k})$ is symmetric. Therefore, by the induction hypothesis,

$\lim _{i\to \infty } \phi (c,c_{i+1},\ldots ,c_{i+k})= \phi (c,d_1,\ldots ,d_{k})$ $(*)$ .

On the other hand, since $\lim _{n\to \infty } tp(c_n/AI)=p|_{AI}$ , we have

$\lim _{n\to \infty }\phi (c_n,d_1,\ldots ,d_{k})=\phi (d_{k+1},d_1,\ldots ,d_{k})$ $(**)$ .

To summarize, for large n,

$$ \begin{align*} \lim_{j\to\infty}\phi(c_j,c_{j+1},\ldots,c_{j+k}) & \stackrel{(\dagger)}{=} \lim_{n\to\infty}\lim_{i\to\infty}\phi(c_n,c_{i+1},\ldots,c_{i+k}) \\ & \stackrel{(*)}{=} \lim_{n\to\infty}\phi(c_n,d_1,\ldots,d_{k}) \\ & \stackrel{(**)}{=} \phi(d_{k+1},d_1,\ldots,d_{k}) \\ & \stackrel{(\ddagger)}{=} \phi(d_1,\ldots,d_{k+1}). \end{align*} $$

This means that $\phi (\bar x)\in SEEM(J/A)$ iff $\phi (\bar x)\in SEM(I/A)$ .

(ii): Let $I'$ be a Morley sequence in p over A. Since T and A are countable, and p is finitely satisfiable in A, there is a sequence $(c_i)$ in A such that $\lim tp(c_i/AI')=p|_{AI'}$ . (Notice that the closure of $\{tp(a/AI'):a\in A\}\subset S_x(AI')$ is second-countable and compact, ⁷ and so metrizable. Therefore, there is a sequence $(c_i)\in A$ such that $\lim tp(c_i/AI')=p|_{AI'}$ .) ⁸

By Fact 2.6, we can assume that $(c_i)$ is eventually indiscernible over $AI (\dagger )$ . That is, the type $EEM((c_i)/AI)$ is complete. (Notice that, as $AI$ and T are countable, using Ramsey’s theorem and a diagonal argument, there is a subsequence of $(c_i)$ which is eventually indiscernible over $AI$ .)

By (i), $SEEM((c_i)/A)=\text {Sym}(p^{(\omega )}|_A)$ .

Remark 2.8. The proof of Lemma 2.7 is essentially the same as [6, Lemma 4.5]. The difference is that we don’t need all formulas, but only symmetric ones. Notice that it is not necessary to assume that A is a model. It is worth recalling that Gannon’s result is based on an idea of Simon [22, Lemma 2.8].

Lemma 2.7 discusses converging of tuples, although in the rest of paper, converging of tuples means convergence of types/tuples over the monster model, but not small sets/models:

Definition 2.9. We say that a sequence $(d_i)\in \cal U$ of x-tuples converges (or is convergent) if the sequence $(tp(d_i/{\cal U}):i<\omega )$ converges in the logic topology. Equivalently, for any $L({\cal U})$ -formula $\phi (x)$ , the truth value of $(\phi (d_i):i<\omega )$ is eventually constant. If $(tp(d_i/{\cal U}):i<\omega )$ converges to a type p, then we write $\lim tp(d_i/{\cal U})=p$ or $tp(d_i/{\cal U})\to p$ . Notice that $tp(d_i/{\cal U})\to p$ iff for any $L({\cal U})$ -formula $\phi (x)$ ,

$$\begin{align*}\lim\phi(d_i)=1 \iff \phi(x)\in p.\end{align*}$$

Fact 2.10. Let $(d_i)$ be a sequence in $\cal U$ of x-tuples. Then the following are equivalent:

(i) $(d_i)$ has a subsequence with no convergent subsequence.

(ii) There are a subsequence $(d_i')\subseteq (d_i)$ and a formula $\phi (x,y)$ (with or without parameters) such that for all (finite) disjoint subsets $E,F\subseteq \Bbb N$ ,

$$\begin{align*}\models\exists y\left(\bigwedge_{i\in E}\phi(d_i',y)\wedge \bigwedge_{i\notin F}\neg\phi(d_i',y)\right).\end{align*}$$

Furthermore, suppose that $(d_i)$ is indiscernible. Then each of (i) and (ii) above is also equivalent to (iii) below:

(iii) The condition (ii) holds for any subsequence of $(d_i)$ . More precisely, there is a formula $\phi (x,y)$ (with or without parameters) such that for any subsequence $(d_i')\subseteq (d_i)$ and for all (finite) disjoint subsets $E,F\subseteq \Bbb N$ ,

$$\begin{align*}\models\exists y\left(\bigwedge_{i\in E}\phi(d_i',y)\wedge \bigwedge_{i\notin F}\neg\phi(d_i',y)\right).\end{align*}$$

Proof The direction (i) $\Rightarrow $ (ii) follows from one of the prettiest result in the Banach space theory due to Rosenthal, Theorem 1 in [20]. (See also Lemma 3.12 of [10] or Appendix B in [11].) Indeed, as T is countable, we can assume ⁹ that there is a subsequence $(c_i)\subseteq (d_i)$ and a formula $\phi (x,y)$ such that the sequence $(\phi (c_i,y):i<\omega )$ has a subsequence with no convergent subsequence. Now use Rosenthal’s theorem for it. (On the other hand, notice that, as T is countable, every complete type can be coded by a function on a suitable space (cf. [13, Appendix A]). This leads to an alternative argument.)

The direction (ii) $\Rightarrow $ (iii) follows from indiscernibility.

(iii) $\Rightarrow $ (ii) $\Rightarrow $ (i) are evident.

We emphasize that, in Fact 2.10, the direction (i) $\Longrightarrow $ (ii) needs countability of the theory. On the other hand, it is easy to verify that, this fact holds for real-valued functions (or types in continuous logic).

Theorem 2.11. Let T be a countable theory, M a countable model, ¹⁰ and $p(x)\in S(\cal U)$ a global type which is finitely satisfiable in M. Let $(d_i)$ be a Morley sequence of p over M. If $(d_i)$ converges then there is a sequence $(c_i)$ in M such that $tp(c_i/{\cal U})\to p$ .

Proof By Lemma 2.7, we can assume that there is a sequence $(c_i)$ in M such that $tp(c_i/M\cup (d_i))\to p|_{M\cup (d_i)}$ and $SEEM((c_i)/M)=\text {Sym}(p^{(\omega )}|_M)$ . We show that $tp(c_i/{\cal U})\to p$ . Let q be an accumulation point of $\{tp(c_i/{\cal U}):i\in \omega \}$ . Then $q|_{M\cup (d_i)}=p|_{M\cup (d_i)}$ . Notice that, as q is finitely satisfiable in M (and so M-invariant), the type $q^{(\omega )}$ is well-defined.

Claim 0: $p^{(\omega )}|_M=q^{(\omega )}|_M$ .

Proof: The proof is by induction. The base case is $q|_{M\cup (d_i)}=p|_{M\cup (d_i)}$ . The induction hypothesis is that $p^{(n+1)}|_M=q^{(n+1)}|_M$ . Let $\phi (x_{n+1},x_n,\ldots ,x_0)\in L(M)$ , and suppose that $p_{x_{n+1}}\otimes p^{(n+1)}_{\bar x} \vdash \phi (x_{n+1},{\bar x})$ , where ${\bar x}=(x_n,\ldots ,x_0)$ . Since $(d_i)$ is a Morley sequence in p over M, $\models \phi (d_{n+1},{\bar d})$ where ${\bar d}=(d_n,\ldots ,d_0)$ . By definition of Morley sequence, $p_{x_{n+1}}\vdash \phi (x_{n+1},{\bar d})$ and ${\bar d}\models p^{(n+1)}_{\bar x}|_M$ . By the hypothesis of induction, ${\bar d}\models q^{(n+1)}_{\bar x}|_M$ . By the base case, $q_{x_{n+1}}\vdash \phi (x_{n+1},{\bar d})$ , and so by definition, $q_{x_{n+1}}\otimes q^{(n+1)}_{\bar x} \vdash \phi (x_{n+1},{\bar x})$ . $\dashv _{\text {claim 0}}$

Claim 1: $p=q$ .

Proof: If not, assume for a contradiction that $p\vdash \phi (x,b)$ and $q\vdash \neg \phi (x,b)$ for some $b\in \cal U$ and formula $\phi (x,y)$ (without parameters). We inductively build a sequence $(a_i)$ as follows:

• If i is even, $a_i\models p|_{M\cup \{a_1, \ldots ,a_{i-1}, b\}}$ .

• If i is odd, $a_i\models q|_{M\cup \{a_1, \ldots ,a_{i-1}, b\}}$ .

As $p^{(\omega )}|_M=q^{(\omega )}|_M$ , the sequence $(a_i)$ is indiscernible and its type over M is $p^{(\omega )}|_M$ . Moreover, $\phi (a_i,b)\iff i \text { is even}$ .

As $(a_i)$ is indiscernible, using the backward direction of [21, Lemma 2.7], ${\cal U}\models \theta _{n,\phi }(a_1,\ldots ,a_n)$ ¹¹ where

$$\begin{align*}\theta_{n,\phi}(x_1,\ldots,x_n)=\forall F\subseteq \{1,\ldots,n\}\exists y_F\left(\bigwedge_{i\in F}\phi(x_i,y_F)\wedge \bigwedge_{i\notin F}\neg\phi(x_i,y_F)\right).\end{align*}$$

(Notice that $\theta _{n,\phi }$ is symmetric, and so $\theta _{n,\phi }\in \text {Sym}(p^{(\omega )}|_M)$ .) This means that $\models \theta _{n,\phi }(d_1,\ldots ,d_n)$ for all n. Therefore, for any infinite subset $I\subseteq \Bbb N$ , the set

$$\begin{align*}\Sigma_I^\phi(y)=\left\{ \bigwedge_{i\in I\cap\{1,\ldots,n\}}\phi(d_i,y)\wedge \bigwedge_{i\notin I\cap\{1,\ldots,n\}}\neg\phi(d_i,y): n\in{\Bbb N}\right\}\end{align*}$$

is a partial type. This means that the sequence $\phi (d_i,y)$ does not converge (and even it has no convergent subsequence), a contradiction. (Alternatively, as both $(a_i),(d_i)$ are Morley sequence over M, there is an automorphism $\sigma \in Aut({\cal U},M)$ which maps $a_i$ to $d_i$ . Then $\phi (d_i,\sigma (b))$ converges iff $\phi (a_i,b)$ converges. ¹² ) $\dashv _{\text {claim 1}}$

Claim 2: The sequence $(tp(c_i/{\cal U}):i<\omega )$ converges.

Proof: If not, without loss of generality we can assume that it has no convergent subsequence. (If $(c_i)$ has a convergent subsequence, we can just choose it to be our sequence and explain why it converges to p.) As T is countable, there is a formula $\psi (x,y)$ (with or without parameters) such that, the sequence $(\psi (c_i,y):i<\omega )$ has no convergent subsequence. ¹³ Then, by Fact 2.10, for any infinite subset $I\subseteq \Bbb N$ , the set

$$\begin{align*}\Sigma_I^\psi(y)=\left\{ \bigwedge_{i\in I\cap\{1,\ldots,n\}}\psi(c_i,y)\wedge \bigwedge_{i\notin I\cap\{1,\ldots,n\}}\neg\psi(c_i,y): n\in{\Bbb N}\right\}\end{align*}$$

is a partial type. As $\theta _{n,\psi }$ is symmetric, this means that $\theta _{n,\psi }\in SEEM((c_i)/M)$ , and so $\models \theta _{n,\psi }(d_1,\ldots ,d_n)$ for all n. Equivalently, $(\psi (d_i,y):i<\omega )$ does not converge, a contradiction. $\dashv _{\text {claim 2}}$

Since $(tp(c_i)/{\cal U}:i\in \omega )$ converges to say a type r, this type is in the topological closure of $\{tp(c_i/{\cal U}):i\in \omega \}$ . Hence by the first portion of the argument, $r=p$ .

Remark 2.12. (i) Let T be a (countable or uncountable) theory, M a model, and $p(x)\in S(\cal U)$ a global type. The argument of Claim 1 in the proof of Theorem 2.11 shows that if there exists a Morley sequence of p which is convergent, then $any$ Morley sequence of p is convergent.

(ii) Let T be a (countable or uncountable) theory, M a model, and $p(x),q(x)$ two global M-invariant types. If the Morley sequence of p is convergent and $p^{(\omega )}|_M=q^{(\omega )}|_M$ , then the argument of Claim 1 in the proof of Theorem 2.11 shows that $p=q$ . ¹⁴ As T is arbitrary, this is a generalization of Proposition 2.36 of [21] (see also Lemma 2.5 of [8]).

(iii) There is a converse to Theorem 2.11: Let T be a countable theory, M a countable model, and $p(x)\in S(\cal U)$ a global type which is finitely satisfiable in M. If there is a sequence $(c_i)$ in M such that $tp(c_i/{\cal U}) DBSC$ -converges to p (as in Definition 3.4), then some/any Morley sequence of p (over M) is convergent. (See the argument of the direction (ii) $\Longrightarrow $ (iii) of Theorem 3.6.)

(iv) (Tanović) Proof of Claim 2 in Theorem 2.11: If not, there are formulas $\psi (x,y)$ (without parameters) and $b\in \cal U$ such that both sets $C_1=\{c_i:\models \psi (c_i,b)\}$ and $C_2=\{c_i:\models \neg \psi (c_i,b)\}$ are infinite. Let $p_1,p_2$ be accumulation points of $\{tp(c_i/{\cal U}):c_i\in C_1\}$ and $\{tp(c_i/{\cal U}):c_i\in C_2\}$ , respectively. Notice that $p_1|_{(d_i)}=p_2|_{(d_i)}$ . We inductively build a sequence $(a_i)$ as follows:

$\bullet $ If i is even, $a_i\models p_1|_{\{a_1,\ldots ,a_{i-1}\}}$ .

$\bullet $ If i is odd, $a_i\models p_2|_{\{a_1,\ldots ,a_{i-1}\}}$ .

Similar to Claim 0, we have $p_1^{(\omega )}|_{(d_i)}=p_2^{(\omega )}|_{(d_i)}$ , and similar to Claim 1, as the Morley sequence $(d_i)$ is convergent, we have $p_1=p_2$ . This is a contradiction, as $p_1\vdash \psi (x,b)$ and $p_2\vdash \neg \psi (x,b)$ . (In fact, it is not necessary to assume that M is a model, and we can assume that $M=(c_i)$ . However, countability remains a key assumption.)

Although with Remark 2.12(iv), we don’t need Fact 2.10, but for better intuition and providing basic concepts in the rest of the article, the approach of Fact 2.10 is useful (cf. Definition 3.1).

Corollary 2.13 [6, Theorem 4.8].

Let T be a countable theory, $p(x)\in S(\cal U)$ and N a (not necessarily countable) model. If p is generically stable over N, then there is a sequence $(c_i)\in N$ such that $tp(c_i/{\cal U})\to p$ .

Proof As T is countable, there is a countable elementary substructure M of N such that p is generically stable over M, and so p is finitely satisfiable in M and every Morley sequence of p is convergent (see also Fact 4.1). Then, by Theorem 2.11, there is a sequence $(c_i)\in M$ such that $tp(c_i/{\cal U})\to p$ .

Notice that in the proof of Theorem 2.11, for any formula $\psi $ there is a natural number n such that $\theta _{n,\psi }\notin SEEM((c_i)/M)$ . This is equivalent to a stronger version of convergence that was studied in [14] and we will recall it in the next section. This implies that our result is strictly stronger than Gannon’s theorem. Cf. Theorem 4.4, the direction (i) $\Rightarrow $ (ii). This is also related to Question 4.15 of [6].

3 Eventual $NIP$

In this section, we want to give a characterization of convergent Morley sequences over countable models. First we introduce the following notions.

Definition 3.1. Let T be a theory, M a model of it and $\phi (x,y)$ a formula (with or without parameters).

(i) We say that $\phi (x,y)$ is eventually $NIP$ in M if for any infinite sequence $(c_i)\in M$ there are a subsequence $(a_i)\subseteq (c_i)$ , a natural number $n=n_{(a_i)}$ and subset $E\subseteq \{1,\ldots ,n\}$ such that for any $i_1<\cdots <i_n<\omega $ , ${\cal U}\models \psi _\phi (a_{i_1},\ldots ,a_{i_n})$ where

$$\begin{align*}\psi_\phi(x_1,\ldots,x_n)=\neg\exists y\left(\bigwedge_{i\in E}\phi(x_i,y)\wedge \bigwedge_{i\in\{1,\ldots,n\}\setminus E}\neg\phi(x_i,y)\right).\end{align*}$$

(ii) We say that M is eventually $NIP$ if every formula is eventually $NIP$ in M.

Note that (i) states that we have a special pattern that never exists. This intuition helps to better understand the notion and how to use it further. In the following, we will explain it better.

Remark 3.2. (i) The subsequence $(a_i)$ in the above is convergent for $\phi $ . ¹⁵ That is, $(\phi (a_i,b):i<\omega )$ converges for any $b\in \cal U$ . Moreover, $\psi _\phi (\bar x)$ is in the Ehrenfeucht–Mostovski type $EM((a_i))$ of $(a_i)$ .

(ii) In some sense, the notion of eventual $NIP$ is not new. In fact, a theory T is $NIP$ (in the usual sense) iff the monster model of T is eventually $NIP$ iff every model of T is eventually $NIP$ iff some model M of T in which all types over the empty set in countably many variables are realized is eventually $NIP$ (cf. Proposition 2.14 in [14]).

(iii) The notion of “eventual $NIP$ ” is strictly stronger than the notion of “ $NIP$ in a model” in [16], and strictly weaker than the notion of “uniform $NIP$ in a model” in [12]. ¹⁶

Let X be a topological space and $f:X\to [0,1]$ be a function. Recall from [14] that f is called a difference of bounded semi-continuous functions (short $DBSC$ ) if there exist bounded semi-continuous functions $F_1$ and $F_2$ on X with $f=F_1-F_2$ . It is a well-known fact that, in general, the class of $DBSC$ functions is a proper subclass of all Baire 1 function (cf. [14, Section 2]).

We let $\phi ^*(y, x)= \phi (x, y)$ . Let $q=tp_{\phi ^*}(b/M)$ be the function $\phi ^*(q,x):M\to \{0,1\}$ defined by $a\mapsto \phi ^*(b,a)$ . This function is called a complete $\phi ^*$ -types over M. The set of all complete $\phi ^*$ -types over M is denoted by $S_{\phi ^*}(M)$ . We equip $S_{\phi ^*}(M)$ with the least topology in which all functions $q\mapsto \phi ^*(q,a)$ (for $a\in M$ ) are continuous. It is compact and Hausdorff, and is totally disconnected.

Definition 3.3. Let $p(x)$ be a global type which is finitely satisfiable in M.

(1) Suppose that $\phi (x,y)$ is a formula, and $p_\phi $ is the restriction of p to $\phi $ -formulas. Define $f_p^\phi :S_{\phi ^*}(M)\to \{0,1\}$ by $f_p^\phi (q)=1$ iff $\phi (x,b)\in p$ for some/any $b\models q$ . We say that:

(i) $p_\phi $ is definable over M if $f_p^\phi $ is continuous.

(ii) $p_\phi $ is $DBSC$ definable over M if $f_p^\phi $ is $DBSC$ .

(iii) $p_\phi $ is Baire 1 definable over M if $f_p^\phi $ is Baire 1.

(2) $p(x)$ is called ( $DBSC$ or Baire 1) definable over M iff for any formula $\phi (x,y)$ the type $p_\phi $ is ( $DBSC$ or Baire 1) definable over M, respectively.

Notice that (i) $\Rightarrow $ (ii) $\Rightarrow $ (iii) but in general (i) $\nLeftarrow $ (ii) $\nLeftarrow $ (iii) (cf. [14]).

Definition 3.4. Let $(a_i)\in \cal U$ be a sequence. We say that $(a_i)$ is $DBSC$ -convergent (or $DBSC$ -converges) if for any formula $\phi (x,y)$ there is a natural number $N=N_\phi $ such that for any $b\in \cal U$ ,

$$\begin{align*}\sum_{i=1}^\infty|\phi(a_i,b)-\phi(a_{i+1},b)|\leq N.\end{align*}$$

In the following we explain the above notions and their relationship.

Remark 3.5. (i) Notice that this notion is equivalent to having finite alternation number. Although, this number depends on both the formula and the sequence; not just on formulas.

(ii) Assuming that $(a_i)$ is eventually indiscernible over the empty set $\emptyset $ . A sequence $(a_i)$ is $DBSC$ -convergent iff for any formula $\phi (x,y)$ (without parameters) there is a formula $\psi _\phi (x_1,\ldots ,x_n)$ , as be in Definition 3.1, such that $\models \psi _\phi (a_{i_1},\ldots ,a_{i_n})$ for any $i_1<\cdots <i_n<\omega $ iff for any formula $\phi (x,y)$ (without parameters) there is a natural number n such that $\theta _{n,\phi }\notin SEEM((a_i)/\emptyset )$ . ¹⁷

(iii) Suppose that $(a_i)$ is $DBSC$ -convergent. Then the sequence $tp(a_i/{\cal U})$ converges. Moreover, for any formula $\phi (x,y)$ the sequence $(tp_\phi (a_i/{\cal U}):i<\omega )$ converges to a type $p_\phi $ which is $DBSC$ definable (over any model $M \supseteq (a_i)$ ).

(iv) Whenever M is countable, $DBSC$ -definability and strong Borel definability (in the sense of [8]) are the same.

Proof (i) was first observed in [14]. (Cf. the paragraph before Remark 2.11 in there.)

(ii) and (iii) follows form Lemma 2.8 of [14]. For the last part of (ii), note that $\models \psi _\phi (a_{i_1},\ldots ,a_{i_n})$ for any $i_1<\cdots <i_n<\omega $ , clearly implies that $\theta _{n,\phi }\notin SEEM((a_i)/\emptyset )$ . For the converse, suppose that there are natural numbers $n, N$ such that for any $N<i_1<\cdots <i_n$ , $\theta _{n,\phi }\notin SEEM((a_i)/\emptyset )$ . Then, we replace $(a_i)$ by $(a_{N+1},a_{N+2},\ldots )$ and use Ramsey’s theorem, if necessary.

(iv) was first mentioned in [14, Remark 2.15] and studied in [13].

We are ready to give a characterization of convergent Morley sequences over countable models in the terms of eventual $NIP$ .

Theorem 3.6. Let T be a countable theory and M a countable model of T. Then the following are equivalent:

(i) is eventually $NIP$ .

(ii) For any $p(x)\in S(\cal U)$ which is finitely satisfiable in M, there is a sequence $(c_i:i<\omega )\in M$ such that the sequence $(tp(c_i/{\cal U}):i<\omega ) DBSC$ -converges to p.

(iii) For any $p(x)\in S(\cal U)$ which is finitely satisfiable in M, there is a Morley sequence $(d_i:i<\omega )$ of p over M such that $(tp(d_i/{\cal U}):i<\omega )$ converges.

Proof (iii) $\Rightarrow $ (i): Let $\phi (x,y)$ be a formula, and $(c_i)$ a sequence in M. Let p be an accumulation point of $\{tp(c_i/{\cal U}):i\in \omega \}$ . (Therefore, p is finitely satisfiable in M.) Let $I=(d_i)$ be a Morley sequence of p over M. By (iii), $(tp(d_i/{\cal U}):i<\omega )$ converges.

Claim: There is a subsequence $(a_i)$ of $(c_i)$ such that $\lim tp(a_i/MI)=p|_{MI}$ . ¹⁸

Proof: The closure of $\{tp(c_i/MI):i<\omega \}\subset S_x(MI)$ is second-countable and compact, and so metrizable. Therefore, there is a sequence $(a_i)\in \{c_i:i<\omega \}$ such that $\lim tp(a_i/MI)=p|_{MI}$ . We can assume that $(a_i)$ is a subsequence of $(c_i)$ . (If not, consider a subsequence of $(a_i)$ which is a subsequence of $(c_i)$ .) $\dashv _{\text {claim}}$

By Fact 2.6, we can assume that $(a_i)$ is eventually indiscernible. Now, by Lemma 2.7, $SEEM((a_i)/M)=SEM((d_i)/M)$ . By Remark 3.5, as $(d_i)$ converges, this means that the condition (i) of Definition 3.1 holds for $(c_i)$ and $\phi (x,y)$ (cf. Remark 2.12(iv)).

(ii) $\Rightarrow $ (iii): Let $p(x)\in S(\cal U)$ be finitely satisfied in M, and $(c_i:i<\omega )\in M$ such that the sequence $(tp(c_i/{\cal U}):i<\omega ) DBSC$ -converges to p. Recall that some Morley sequence of p over M is convergent if and only if every Morley sequence of p over M is convergent. Let $I=(d_i)$ be a Morley sequence in p over M. By (ii), $\lim tp(c_i/MI)=p|_{MI}$ , and so by Lemma 2.7, we have $SEEM((c_i)/M)=SEM((d_i)/M)$ . As $(tp(c_i/{\cal U}):i<\omega )$ is $DBSC$ -convergent, by Remark 3.5, $(d_i)$ converges.

(i) $\Rightarrow $ (ii): Let $p(x)\in S(\cal U)$ be finitely satisfied in M. By Lemma 2.7, there are a sequence $(c_i)$ in M and a Morley sequence $(d_i)$ of p over M such that $tp(c_i/M\cup (d_i))\to p|_{M\cup (d_i)}$ and $SEEM((c_i)/M)=SEM((d_i)/M)$ . By (i), as T is countable, using a diagonal argument, there is a subsequence $(c_i')\subseteq (c_i)$ such that $(tp(c_i'/{\cal U}):i<\omega ) DBSC$ -converges. Therefore, using an argument similar to the proof of Claim 2 in Theorem 2.11 (or directly), we can see that the Morley sequence $(d_i)$ is convergent. By an argument similar to Theorem 2.11, $(tp(c_i'/{\cal U}):i<\omega )$ converges to p (cf. Remark 2.12(iv)).

Remark 3.7. Let T be a countable theory and M a countable model of it. Suppose that any $p(x)\in S(\cal U)$ which is finitely satisfied in M is $DBSC$ definable over M. In this case, using the BFT theorem, it is easy to show that for any such type $p(x)$ there is a sequence $(c_i)\in M$ such that $\lim tp(c_i/{\cal U})=p$ . Notice that there is no reason that $(tp(c_i/{\cal U}):i<\omega ) DBSC$ -converges to p. A question arises. With the above assumptions, for any $p(x)\in S(\cal U)$ which is finitely satisfied in M, is there any sequence $(c_i)\in M$ such that $(tp(c_i/{\cal U}):i<\omega ) DBSC$ -converges to p? We believe that the answer is negative, although we have not found a counterexample yet.

3.1 An application to definable groups

To finish this section, we give an example where the notion of eventual $NIP$ is used to deduce results about definable groups.

Lemma 3.8. Let G be a definable group. Let $p,q$ be invariant types concentrating on G such that both $p_x\otimes q_y$ and $q_y\otimes p_x$ imply $x\cdot y= y\cdot x$ . ¹⁹ If some/any Morley sequence of p converges, then $a\cdot b= b\cdot a$ for any $a\models p$ and $b\models q$ .

Proof The proof is an adaptation of [21, Lemma 2.26]. By compactness, there is a small model M such that $p,q$ are M-invariant and for any $(a,b)$ realizing one of $(p\otimes q)|_M$ or $(q\otimes p)|_M$ we have $a\cdot b= b\cdot a$ .

We claim that there is no infinite sequence $(a_n b_n:n<\omega )$ such that $a_n\models p|_{Ma_{<n}b_{<n}}$ , $b_n\models q|_{Ma_{<n}b_{<n}}$ and $a_n\cdot b_n\neq b_n\cdot a_n$ . If not, by hypothesis $a_n\cdot b_m= b_m\cdot a_n$ for $n\neq m$ . For any $I\subset \omega $ finite, define $b_I=\prod _{n\in I}b_n$ . Therefore, $a_n\cdot b_I= b_I\cdot a_n$ if and only if $n\notin I$ . This means that the sequence $(\phi (a_n,y):N<\omega )$ does not converges where $\phi (a_n,y):=a_n\cdot y\neq y\cdot a_n$ . As $(a_n:n<\omega )$ is a Morley sequence of p, this contradicts the assumption.

Therefore, by the above claim, there is some n such that any sequence with the above construction has the length smaller than n. Let $p_0=p|_{Ma_{<n}b_{<n}}$ and $q_0=q|_{Ma_{<n}b_{<n}}$ . Then $p_0(x)\wedge q_0(y)\rightarrow x\cdot y= y\cdot x$ .

Proposition 3.9. Let T be a countable theory and G a definable group. Assume that there is a countable subset $A\subset G$ such that any two elements of A commute, and A is eventually $NIP$ . Then there is a definable abelian subgroup of G containing A.

Proof Let $S_A\subset S({\cal U})$ be the set of global $1$ -types finitely satisfiable in A. Notice that, as A is eventually $NIP$ , by Theorem 3.6, the Morley sequence of any type in $S_A$ is convergent. Therefore, for any $p,q\in S_A$ , the pair $(p,q)$ satisfies the hypothesis of Lemma 3.8. The rest is similar to the argument of Proposition 2.27 of [21]. Indeed, by Lemma 3.8 and compactness, one can find formulas $\phi (x)$ and $\psi (y)$ such that $\phi (x)\wedge \psi (y)\rightarrow x\cdot y=y\cdot x$ and all types of $S_A$ concentrate on both $\phi (x)$ and $\psi (y)$ . Set $H:=C_G(C_G(\phi \wedge \psi ))$ , where $C_G(X)=\{g\in G:g\cdot x=x\cdot g \text { for all } x\in X\}$ . Then H is a definable abelian subgroup of G containing A.

Remark 3.10. (1) Notice that, if any two elements of a set A commute, then $C_G(C_G(A))$ is abelian, but $C_G(A)$ is not automatically abelian (even when A is a subgroup). ²⁰ In the following, we provide a proof:

Notice that, as any two elements of A commute, $A\subseteq C_G(A)$ . Therefore $C_G(A)\supseteq C_G(C_G(A))$ . ²¹ Let $a,b\in C_G(C_G(A))$ . Since $b\in C_G(A)$ , so by definition $ab=ba$ . As $a,b$ are arbitrary, $C_G(C_G(X))$ is abelian. ²²

(2) In Proposition 3.9, if A is finite, we don’t need eventual $NIP$ : take $H=C_G(C_G(A))$ .

4 Generically stable types

Here we want to give new characterizations of generically stable types for countable theories. The notion of generically stable types in general theories was introduced in [18]. Recall from [4, Proposition 3.2] that a global type p is generically stable over a small set A if p is A-invariant and for any Morley sequence $(a_i:i<\omega )$ of p over A, we have $\lim tp(a_i/{\cal U})=p$ .

Before giving the results let us recall that:

Fact 4.1 [6, Fact 2.6].

Let M be small set, and $p(x)\in S({\cal U})$ a global M-invariant type.

(i) If p is generically stable over M, then p is definable over and finitely satisfiable in M.

(ii) If p is generically stable over M and $M_0$ -invariant, then p is generically stable over $M_0$ . If p is definable over and finitely satisfiable in M and $M_0$ -invariant, the same holds.

(iii) Assuming that T is countable, if p is generically stable over M, there exists a countable elementary substructure $M_0$ such that p is generically stable over $M_0$ . The same holds for definable and finitely satisfiable case.

Lemma 4.2. Let T be a (countable or uncountable) theory, $A\subset {\cal U}$ , and $p(x)\in S({\cal U})$ a global A-invariant type. Suppose that some/any Morley sequence of p is totally indiscernible, AND some/any Morley sequence of p is convergent. Then p is generically stable. ²³

Proof Let $I=(a_i)$ be a Morley sequence of p over A. We show that $\lim tp(a_i/{\cal U})=p$ . Let $\phi (x,b)\in p$ and $J\models p^{(\omega )}|_{AIb}$ . Set $I_n=(a_1,\ldots ,a_n)$ for all n. Notice that all points of J satisfy $\phi (x,b)$ , and $I_n+J$ is a Morley sequence (for all n). ²⁴ We claim that at most a finite number of points of I satisfy $\neg \phi (x,b)$ . If not, for each k, there is a natural number $n_k$ such that $\#\{a_i\in I_{n_k}:\models \neg \phi (a_i,b)\}\geq k$ . As $I_n+J$ is totally indiscernible (for all n), this implies that for each n, $\theta _{n,\phi }(x_1,\ldots ,x_n)\in tp(J)$ where

$$\begin{align*}\theta_{n,\phi}(x_1,\ldots,x_n)=\forall F\subseteq \{1,\ldots,n\}\exists y_F\left(\bigwedge_{i\in F}\phi(x_i,y_F)\wedge \bigwedge_{i\notin F}\neg\phi(x_i,y_F)\right).\end{align*}$$

(Recall that $\theta _{n,\phi }$ was introduced in the proof of Theorem 2.11. Notice that if $\#\{i: \models \phi (a_i,b)\}=\aleph _0$ then we do not need total indiscernibility, but only indiscernibility.) Equivalently, J is not convergent, a contradiction.

Remark 4.3. Let T be a (countable or uncountable) theory, $A\subset {\cal U}$ , and $p(x)\in S({\cal U})$ a global A-invariant type. The following are equivalent.

(i) $p$ is generically stable.

(ii) $p$ is definable over a small model AND there is a Morley sequence $(a_i:i<\omega )$ of p over A such that $\lim tp(a_i/{\cal U})=p$ .

Proof (i) $\Longrightarrow $ (ii) follows from Fact 4.1 (cf. [21, Theorem 2.29]).

(ii) $\Longrightarrow $ (i): Suppose that there is a Morley sequence $I=(a_i)$ of p over A such that $\lim I=p$ . As p is definable and finitely satisfiable, some/any Morley sequence of p is totally indiscernible. (Cf. [12, Corollary 4.11] for a proof that any definable and finitely satisfiable type commutes with itself and a generalization to measures.) Therefore, by Lemma 4.2, p is generically stable.

The following theorem gives new characterizations of generically stable types for countable theories. The important ones to note immediately are (ii) and (v).

Theorem 4.4. Let T be a countable theory, M a small model of T, and $p(x)\in S({\cal U})$ a global M-invariant type. The following are equivalent:

(i) p is generically stable over M.

(ii) p is definable over a small model, AND there is a sequence $(c_i)$ in M such that $(tp(c_i/{\cal U}):i<\omega ) DBSC$ -converges to p.

(iii) p is definable over and finitely satisfiable in some small model, AND there is a convergent Morley sequence of p over M.

(iv) p is definable over a small model, AND there is a Morley sequence $(a_i)$ of p over M such that $\lim tp(a_i/{\cal U})=p$ . Suppose moreover that T has $NSOP$ , then each of (v)–(vii) below is also equivalent to (i)–(iv) above.

(v) There is a sequence $(c_i)$ in M such that $(tp(c_i/{\cal U}):i<\omega ) DBSC$ -converges to p.

(vi) p is finitely satisfiable in a countable model $M_0\prec M$ , AND there is a convergent Morley sequence of p over M.

(vii) There is a Morley sequence $(a_i)$ of p over M such that $\lim tp(a_i/{\cal U})=p$ .

Proof (i) $\Longrightarrow $ (ii): As T is countable, by Fact 4.1, we can assume that p is generically stable over a countable substructure $M_0 \prec M$ . By Corollary 2.13, there is a sequence $(c_i)$ in M such that $(tp(c_i/{\cal U}):i<\omega )$ converges to p. Notice that in the proof of Theorem 2.11 for any formula $\phi $ there is a natural number n such that the formula $\theta _{n,\phi }$ does not belong to $SEEM((c_i)/M)$ . This means that $(tp(c_i/{\cal U}):i<\omega )$ is $DBSC$ -convergent.

(ii) $\Longrightarrow $ (i): Clearly, p is finitely satisfiable in M. As p is definable and finitely satisfiable, any Morley sequence of p is totally indiscernible (cf. [12, Corollary 4.11]). Let $(d_i)$ be a Morley sequence of p over M. By Fact 2.6, we can assume that $(c_i)$ is eventually indiscernible over $M\cup (d_i)$ . By Lemma 2.7, it is easy to see that $SEEM((c_i)/M)=SEM((d_i)/M)$ . Therefore, as $(c_i)$ is $DBSC$ -convergent, the Morley sequence $(d_i)$ converges. By Lemma 4.2, p is generically stable.

(iii) $\Longrightarrow $ (i) follows from Lemma 4.2 and the fact that the Morley sequences of definable and finitely satisfiable types are totally indiscernible.

(i) $\Longrightarrow $ (iii) follows from the direction (i) $\Longrightarrow $ (ii) of [4, Proposition 3.2]. (Recall that generically stable types are definable and finitely satisfiable.)

(iv) $\iff $ (i) follows from Remark 4.3.

The directions (ii) $\Longrightarrow $ (v) and (iii) $\Longrightarrow $ (vi) and (iv) $\Longrightarrow $ (vii) are evident (and hold in any theory).

For the rest of the proof, suppose moreover that T has $NSOP$ .

Then, (v) $\Longrightarrow $ (ii) follows from Proposition 2.10 of [14] and the Eberlein–Grothendieck criterion [14, Fact 2.2]. Indeed, by the direction (i) $\Longrightarrow $ (iv) of [14, Proposition 2.10], for any formula $\phi (x,y)$ , there is no infinite sequence $(b_j)$ such that $\phi (c_i,b_j)$ holds iff $i<j$ . By Fact 2.2 of [14], this means that the limit of $(\phi (c_i,y):i<\omega )$ is a continuous function. Equivalently, p is definable over M (see also Remark 2.11 of [14]).

(vi) $\Longrightarrow $ (iii): Suppose that p is finitely satisfiable in $M_0\prec M$ with $|M_0|=\aleph _0$ . By Theorem 2.11, there is a sequence $(c_i)\in M_0$ such that $(tp(c_i/{\cal U}):i<\omega ) \mathit{DBSC}$ -converges to p. By the direction (i) $\Longrightarrow $ (iv) of [14, Proposition 2.10 and Fact 2.2], p is definable over $M_0$ . Therefore, (iii) holds.

(vii) $\Longrightarrow $ (iv): As $(a_i)$ is indiscernible and convergent, the sequence $(tp(a_i/{\cal U}):i<\omega )$ is $DBSC$ -convergent. This means, by $NSOP$ (i.e., the direction (i) $\Longrightarrow $ (iv) of [14, Proposition 2.10 and Fact 2.2]), that p is definable.

Remark 4.5. (i) It is not hard to give a variant of Theorem 4.4 for uncountable theories. Indeed, we can consider all countable fragments of the languages, and use the above argument.

(ii) With the assumption of Theorem 4.4, then $(*)$ below is also equivalent to (i)–(iv) in Theorem 4.4:

$(*)$ For any $B\supset M$ , p is the unique global nonforking extension of $p|_B$ , AND there is a convergent Morley sequence of p over M.

The argument is an adaptation of the proof of [8, Proposition 3.2]. See also Proposition 4.6(ii).

As the referee pointed out to us, the following proposition is not new. ²⁵ Although for the sake of completeness we give a proof using the above observations.

Proposition 4.6. Let T be a (countable or uncountable) theory and p a generically stable type.

(i) For any invariant type q, $p\otimes q=q\otimes p$ .

(ii) If p is A-invariant, then p is the unique A-invariant extension of $p|_A$ .

Proof (i) follows from the argument of Proposition 2.33 of [21] by replacing [21, Lemma 2.28] with the argument of Lemma 4.2. Indeed, suppose for a contradiction that for some formula $\phi (x,y,c)\in L({\cal U})$ (where c is a tuple of elements) we have $p_x\otimes q_y\vdash \phi (x,y,c)$ and $q_y\otimes p_x\vdash \neg \phi (x,y,c)$ . Let $(a_i:i<\omega )\models p^{(\omega )}$ , $b\models q|_{{\cal U}a_{<\omega }}$ and $(a_i:\omega \leq i<\omega 2)\models p^{(\omega )}|_{{\cal U}a_{<\omega }b}$ . Then for $i<\omega $ , $\neg \phi (a_i,b,c)$ holds and for $i\geq \omega $ , we have $\phi (a_i,b,c)$ . (Recall the definition of Morley products in 2.2.1 of [21].) As $(a_i:i<\omega 2)$ is totally indiscernible, similar to the argument of Lemma 4.2, it is easy to verify that for each n, $\theta _{n,\phi }(x_1,\ldots ,x_n)\in tp((a_i)/\emptyset )$ where

$$\begin{align*}\theta_{n,\phi}(x_1,\ldots,x_n)=\forall F\subseteq \{1,\ldots,n\}\exists y_F\exists y_c\left(\bigwedge_{i\in F}\phi(x_i,y_F,y_c)\wedge \bigwedge_{i\notin F}\neg\phi(x_i,y_F,y_c)\right).\end{align*}$$

Equivalently, the sequence $(\phi (a_i, y_F,y_c):i<\omega )$ is not convergent, a contradiction.

(ii): Let q be any A-invariant extension of $p|_A$ .

Claim: $p^{(\omega )}|_A=q^{(\omega )}|_A$ .

Proof: The proof is by induction, and similar to the argument of Proposition 2.35 of [21]. The base case is $p|_A=q|_A$ . The induction hypothesis is that $p^{(n)}|_A=q^{(n)}|_A$ . Using (i) above and associativity of Morley products, we have

$$ \begin{align*} q^{(n+1)}_{x_1,\ldots,x_{n+1}}|_A & = (q_{x_{n+1}}\otimes q^{(n)}_{x_1,\ldots,x_{n}})|_A \\ & = (q_{x_{n+1}}\otimes p^{(n)}_{x_1,\ldots,x_{n}})|_A \\ & \stackrel{(*)}{=} (p^{(n)}_{x_1,\ldots,x_{n}}\otimes q_{x_{n+1}})|_A \\ & = (p^{(n)}_{x_1,\ldots,x_{n}}\otimes p_{x_{n+1}})|_A \\ & = p^{(n+1)}_{x_1,\ldots,x_{n+1}}|_A. \end{align*} $$

Notice that (i) and associativity of Morley products are used in $(*)$ . ²⁶ $\dashv _{\text {claim}}$

Therefore, every Morley sequence of q is totally indiscernible AND convergent. By Lemma 4.2, q is generically stable and so $\lim I=q$ for any Morley sequence of q. This means that $p=\lim I=q$ for any $I=p^{(\omega )}|_A=q^{(\omega )}|_A$ . (Alternatively, as $p^{(\omega )}|_A=q^{(\omega )}|_A$ , one can use Remark 2.12(ii) above.)

Here we want to give a local version of a classical result [8, Proposition 3.2].

Theorem 4.7. Let T be a (countable or uncountable) theory, M be a model of T, and $p(x)$ a global M-invariant type. Suppose that there is an elementary extension $M'\succ M$ containing a Morley sequence of p such that $M'$ is eventually $NIP$ . Then the following are equivalent.

(i) $p=\lim tp(a_i/{\cal U})$ for any $(a_i)\models p^{(\omega )}|_M$ .

(ii) p is definable over and finitely satisfiable in M.

(iii) $p_x\otimes p_y=p_y\otimes p_x$ .

(iv) Any Morley sequence of p is totally indiscernible.

Proof (i) $\Longrightarrow $ (ii) $\Longrightarrow $ (iii) $\Longrightarrow $ (iv) are standard and hold in any theory (cf. Theorem 2.29 of [21]).

(iv) $\Longrightarrow $ (i): Let $J\in M'$ be a Morley sequence of p. Since $M'$ is eventually $NIP$ , the sequence J is convergent. By Lemma 4.2, p is generically stable.

Notice that the above theorem holds with a weaker assumption, namely every formula has $NIP$ in $M'$ (cf. [16] for the definition of $NIP$ in a model). This easily follows from indiscernibility of Morley sequences.

4.1 Eventually stable models

The story started from Grothendieck’s double limit characterization of weak relative compactness, Theorem 6 in [7]. In [1] Ben Yaacov showed that the “Fundamental Theorem of Stability” is in fact a consequence of Grothendieck’s theorem. Shortly afterwards, Pillay [17] pointed out that the model-theoretic meaning of the Grothendieck theorem is that the formula $\phi (x,y)$ does not have the order property in M if and only if every complete $\phi $ -type $p(x)\in S_\phi (M)$ has an extension to a complete type $p'\in S_\phi ({\cal U})$ which is finitely satisfiable in, and definable over M. There, he called such types “generically stable” and said: “We will investigate later to what extent we can deduce the stronger notions of generic stability from not the order property in M.” Here, using the previous results/observations, we can prove a result similar to [17] for the stronger notions of generic stability. Maybe the following result is the end of this story, and of course the beginning of another story.

Definition 4.8. Let M be a model. (i) We say that M has no order if for any formula $\phi (x,y)$ there do not exist $(a_i),(b_i)$ in M for $i<\omega $ such that $M\models \phi (a_i,b_j)$ iff $i\leq j$ .

(ii) We say that M is eventually stable if:

(1) M has no order, and

(2) M is eventually $NIP$ (as in Definition 3.1).

Remark 4.9. (i) In stable theories, every model is eventually stable.

(ii) In $NIP$ theories, every model which has no order is eventually stable.

Proof (i): If not, similar to the argument of (i) $\Rightarrow $ (iii) of [14, Proposition 2.14], we can find a formula $\phi (x,y)$ , an indiscernible sequence $(c_i)$ , and an element d such that $\phi (c_i,d)$ holds if and only if i is even. This contradicts $NIP$ .

(ii) Suppose that the theory T is $NIP$ and $M\models T$ has no order. Suppose for a contradiction that M is not eventually $NIP$ . Similar to (i), we can find a formula $\phi (x,y)$ , an indiscernible sequence $(c_i)$ (possibly in an elementary extension of M), and an element $d\in \cal U$ such that $\phi (c_i,d)$ holds if and only if i is even, a contradiction.

Theorem 4.10. Let T be a (countable or uncountable) theory, and M be a model of T. The following are equivalent:

(i) M is eventually stable.

(ii) Any type $p\in S_x(M)$ has an extension to a global type $p'\in S_x({\cal U})$ which is generically stable over M.

Proof First, without loss of generality we can assume that T is countable. ²⁷ By Proposition 2.3(c) of [17], M has no order if and only if any type $p\in S_x(M)$ has an extension to a global type $p'\in S_x({\cal U})$ which is finitely satisfiable in, and definable over M. ²⁸ By Theorems 3.6 and 4.4, any global type $p'\in S_x({\cal U})$ which is finitely satisfiable in, and definable over M is generically stable over M if and only if M is eventually $NIP$ . This proves the theorem.

4.2 Concluding remarks/questions

(1) In Example 2.18 of [14], we built a graph N with the following property: (i) there is a sequence $(a_i)\in N$ such that $R(a_i,y)$ converges, and (ii) $R(a_i,y)$ is not $DBSC$ -convergent. We guess that a modification of this example leads to a definable type p such that: (i) there is a sequence $(a_i)$ with $\lim tp(a_i/{\cal U})=p$ , and (ii) p is not the limit of any $DBSC$ -convergent sequence. (For this, one need to remove the axiom schema (1) in Example 2.18, and to check the above properties.) Therefore, by Theorem 4.4, p is not generically stable. This approach probably answer to Question 4.15 of [6].

(2) These results/observations can be generalize to “continuous logic” [2]. On the other hand, one can generalize Theorem 3.6 for measures in classical logic. This is a generalization of another result of Gannon [6, Theorem 5.10]. Recall that measures in classical logic correspond to types in continuous logic. This means that a generalization of Theorem 3.6 to continuous logic leads to a generalization of this theorem for measures in classical logic, and vice versa.

(3) In [11], we claimed that in the language of Banach spaces in continuous logic, there is a Krivine–Maurey type theorem for $NIP$ theories (or even $NIP$ spaces). That is, for any separable $NIP$ space X there exists a spreading model of X containing $c_0$ or $\ell _p$ for some $1\leq p<\infty $ . We believe that the results/observations of the present paper are sufficient tools and they lead to a proof of this conjuncture. For example, notice that $EEM$ -types correspond to spreading models in Banach space theory. On the other hand, types of $c_0$ and $\ell _p$ are symmetric in a strong sense. Finally, the types of $c_0$ or $\ell _p$ are finitely satisfied in any Banach space, by Krivine’s theorem.

(4) In [11], we showed that every $\aleph _0$ -categorical Banach space contains $c_0$ or $\ell _p$ . What is the translation of this observation into “classical logic” (if such a translation is essentially possible)? Similar questions can be asked about the Krivine–Maurey theorem (and the claim in (3) whenever a proof of it is given).

We will study them elsewhere. (See, for example, [15] for (2).)