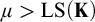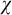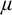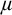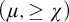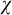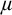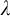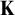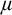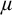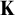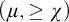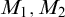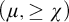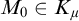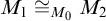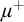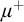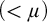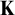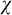STABILITY RESULTS ASSUMING TAMENESS, MONSTER MODEL, AND CONTINUITY OF NONSPLITTING

Abstract

Assuming the existence of a monster model, tameness, and continuity of nonsplitting in an abstract elementary class (AEC), we extend known superstability results: let $\mu>\operatorname {LS}(\mathbf {K})$ be a regular stability cardinal and let $\chi $ be the local character of $\mu $-nonsplitting. The following holds:

1. 1. When $\mu $-nonforking is restricted to $(\mu ,\geq \chi )$-limit models ordered by universal extensions, it enjoys invariance, monotonicity, uniqueness, existence, extension, and continuity. It also has local character $\chi $. This generalizes Vasey’s result [37, Corollary 13.16] which assumed $\mu $-superstability to obtain same properties but with local character $\aleph _0$.

2. 2. There is $\lambda \in [\mu ,h(\mu ))$ such that if $\mathbf {K}$ is stable in every cardinal between $\mu $ and $\lambda $, then $\mathbf {K}$ has $\mu $-symmetry while $\mu $-nonforking in (1) has symmetry. In this case:

   1. (a) $\mathbf {K}$ has the uniqueness of $(\mu ,\geq \chi )$-limit models: if $M_1,M_2$ are both $(\mu ,\geq \chi )$-limit over some $M_0\in K_{\mu }$, then $M_1\cong _{M_0}M_2$;

   2. (b) any increasing chain of $\mu ^+$-saturated models of length $\geq \chi $ has a $\mu ^+$-saturated union. These generalize [31] and remove the symmetry assumption in [10, 38] .

Under $(<\mu )$-tameness, the conclusions of (1), (2)(a)(b) are equivalent to $\mathbf {K}$ having the $\chi $-local character of $\mu $-nonsplitting.

Grossberg and Vasey [18, 38] gave eventual superstability criteria for tame AECs with a monster model. We remove the high cardinal threshold and reduce the cardinal jump between equivalent superstability criteria. We also add two new superstability criteria to the list: a weaker version of solvability and the boundedness of the U-rank.

1 Introduction

The notion of abstract elementary classes (AECs) was created by Shelah [22] to encompass certain classes of models, including models of first-order theories. To develop the classification theory of AECs, notions like types, stability, and superstability were generalized to the AEC context. Superstability is a major topic in AECs because it is implied by categoricity and has good transfer properties (assuming tameness and a monster model). Early results could be found in [17, 23, 26–28], which were later extended by Boney, Grossberg, VanDieren, and Vasey.

Guided by the first-order case, Grossberg and Vasey [18] provided several equivalent definitions of superstability for AECs: no long splitting chains, existence of a good frame, existence of a unique limit model, existence of a superlimit model, solvability, and that the union of an increasing chain of $\lambda $ -saturated models is $\lambda $ -saturated (where $\lambda $ is high enough). Later Vasey [38, Corollary 4.24] added the (expected) criterion of stability in a tail. However, their results had two drawbacks:

1. 1. The cardinal threshold was high (the first Hanf number): if an AEC satisfies one of the criteria in $\operatorname {LS}(\mathbf {K})$ or ${\operatorname {LS}(\mathbf {K})}^+$ , it does not necessarily imply any other criterion.

2. 2. The cardinal jump was high between equivalent criteria: if an AEC satisfies one of the criteria in a (high-enough) cardinal $\lambda $ , it was only known that other criteria hold in a much bigger cardinal (sometimes $\beth _\omega (\lambda )$ ).

In this paper, we aim to refine the list of equivalent superstability criteria using known techniques in the literature. We reduce the cardinal threshold to ${\operatorname {LS}(\mathbf {K})}^+$ and the cardinal jump to a successor cardinal. The missing piece in [18] was to show the uniqueness of limit models from no long splitting chains. The original approach used Galois-Morleyization and averages [11] at the cost of a high cardinal jump. We observe that the tower approach from [31] is cleaner and has no cardinal jump, which allows us to rewrite many results in the literature that involve the uniqueness of limit models.

On the other hand, the equivalent criteria of superstability in first-order theories have their strictly-stable analogues. For example, when the local character of forking $\kappa (T)$ is uncountable, the union of an increasing chain of $\lambda $ -saturated models is $\lambda $ -saturated, provided that the chain has cofinality at least $\kappa (T)$ . This motivates us to look for generalizations of the superstability criteria. It turns out that a key assumption is “continuity of nonsplitting,” which allows us to mimick the proofs of many superstable results. Such assumption was partially explored in [10, 38] but a full picture was yet to be seen. It seems that the study of stability is much more difficult without assuming continuity of nonsplitting: Vasey [38] gave some eventual results of stability which were only applicable to high cardinals.

In the following, we provide an overview of the upcoming sections and highlight some key theorems: Section 2 states the global assumptions and preliminaries. Section 3 studies the properties of nonsplitting, which will be used to build good frames in Section 4. The idea of good frames was developed in [24, IV Theorem 4.10], assuming categoricity and non-ZFC axioms, in order to deduce nice structural properties of an AEC. Later Boney and Grossberg [6] built a good frame from coheir with the assumption of tameness and extension property of coheir in ZFC. Vasey [34, Section 5] further developed on coheir and [32] managed to construct a good frame at a high categoricity cardinal (categoricity can be replaced by superstability and type locality, but the initial cardinal of the good frame is still high).

Another approach to building a good frame is via nonsplitting. It is in general not clear whether uniqueness or transitivity hold for nonsplitting (where models are ordered by universal extensions). To resolve this problem, Vasey [33] constructed nonforking from nonsplitting, which has nicer properties: assuming superstability in $K_{\mu }$ , tameness, and a monster model, nonforking gives rise to a good frame over the limit models in $K_{\mu ^+}$ [31, Corollary 6.14]. Later it was found that uniqueness of nonforking also holds for limit models in $K_{\mu }$ [35].

We will generalize the nonforking results by replacing the superstability assumption by continuity of nonsplitting. A key observation is that the extension property of nonforking still holds if we have continuity of nonsplitting and stability. This allows us to replicate extension, uniqueness, and transitivity properties. Since the assumption of continuity of nonsplitting applies to universal extensions only, we only get continuity and local character for universal extensions. Hence we can build an approximation of a good frame which is over the skeleton (see Definition 2.4) of long enough limit models ordered by universal extensions. We state the known result and our result for comparison.

Theorem 1.1. Let $\mu \geq \operatorname {LS}(\mathbf {K})$ , $\mathbf {K}$ have a monster model, be $\mu $ -tame and stable in $\mu $ . Let $\chi $ be the local character of $\mu $ -nonsplitting.

1. 1. [37, Corollary 13.16] If $\mathbf {K}$ is $\mu $ -superstable, then there exists a good frame over the skeleton of limit models in $K_{\mu }$ ordered by $\leq _u$ , except for symmetry.

2. 2. (Corollary 4.13) If $\mu $ is regular and $\mathbf {K}$ has continuity of $\mu $ -nonsplitting, then there exists a good $\mu $ -frame over the skeleton of $(\mu ,\geq \chi )$ -limit models ordered by $\leq _u$ , except for symmetry. The local character is $\chi $ in place of ${\aleph _0}$ .

In Section 5, we will deduce symmetry under extra stability assumptions. In Section 6, we will generalize known superstability results using the symmetry properties. Symmetry is an important property of a good frame that connects superstability and the uniqueness of limit models. To obtain symmetry for our frame, we look into the argument in [31]. In [29, 30], VanDieren defined a stronger version of symmetry called $\mu $ -symmetry and proved its equivalence with the continuity of reduced towers. VanDieren and Vasey [31, Lemma 4.6] noticed that a weaker version of symmetry is sufficient in one direction and deduced the weaker version of symmetry via superstability. To generalize these arguments, we replace superstability by continuity of nonsplitting and stability in a range of cardinals (the range depends on the no order property of $\mathbf {K}$ , see Proposition 5.9). Then we can obtain a local version of $\mu $ -symmetry, which implies symmetry of our frame for long enough limit models.

Theorem 1.2. Let $\mu \geq \operatorname {LS}(\mathbf {K})$ , $\mathbf {K}$ be $\mu $ -tame and stable in $\mu $ . Let $\chi $ be the local character of $\mu $ -nonsplitting.

1. 1. [31, Corollary 6.9] If $\mathbf {K}$ is $\mu $ -superstable, then it has $\mu $ -symmetry.

2. 2. (Corollary 5.13) If $\mu $ is regular and $\mathbf {K}$ has continuity of $\mu $ -nonsplitting. There is $\lambda <h(\mu )$ such that if $\mathbf {K}$ is stable in every cardinal between $\mu $ and $\lambda $ , then $\mathbf {K}$ has $(\mu ,\chi )$ -symmetry.

The notions of continuity of nonsplitting and of local symmetry were already exploited in [10, Theorem 20] to obtain the uniqueness of long enough limit models (see Fact 6.1). They simply assumed the local symmetry while we used the argument in [31] to deduce it from extra stability and continuity of nonsplitting (Corollary 6.2). On the other hand, [38, Section 11] used continuity of nonsplitting to deduce that a long enough chain of saturated models of the same cardinality is saturated. There he assumed saturation of limit models and managed to satisfy this assumption using his earlier result with Boney [11], which has a high cardinal threshold. Since we already have local symmetry under continuity of nonsplitting and extra stability, we immediately have uniqueness of long limit models, and hence Vasey’s argument can be applied to obtain the above result of saturated models (see Proposition 6.6; a comparison table of the approaches can be found in Remark 6.8(2)).

Vasey [38, Lemma 11.6] observed that a localization of VanDieren’s result [29] can give: if the union of a long enough chain of $\mu ^+$ -saturated models is $\mu ^+$ -saturated, then local symmetry is satisfied. Assuming more tameness, we use this observation to obtain converses of our results (see Main Theorem 8.1(4) $\Rightarrow $ (3)). In particular, local symmetry will lead to uniqueness of long limit models, which implies local character of nonsplitting (Main Theorem 8.1(3) $\Rightarrow $ (1)). Despite the important observation by Vasey, he did not derive these implications.

Theorem 1.3. Let $\mu>\operatorname {LS}(\mathbf {K})$ , $\delta \leq \mu $ be regular, $\mathbf {K}$ have a monster model, be $(<\mu )$ -tame, stable in $\mu $ and has continuity of $\mu $ -nonsplitting. If any increasing chain of $\mu ^+$ -saturated models of cofinality $\geq \delta $ has a $\mu ^+$ -saturated union, then $\mathbf {K}$ has $\delta $ -local character of $\mu $ -nonsplitting.

In the original list inside [18], $(\lambda ,\xi )$ -solvability was considered for $\lambda>\xi $ , which they showed to be an equivalent definition of superstability, with a huge jump of cardinal from no long splitting chains to solvability. Further developments in [36] indicate that such solvability has downward transfer properties which seems too strong to be called superstability. We propose a variation where $\lambda =\xi $ and will prove its equivalence with no long splitting chains in the same cardinal above $\mu ^+$ (under continuity of nonsplitting and stability). At $K_{\mu }$ , we demand $(<\mu )$ -tameness for the equivalence to hold, up to a jump to the successor cardinal.

Theorem 1.4. Let $\mu>\operatorname {LS}(\mathbf {K})$ , $\mathbf {K}$ have a monster model, be $(<\mu )$ -tame, stable in $\mu $ .

1. 1. [26] If there is $\lambda>\mu $ such that $\mathbf {K}$ is $(\lambda ,\mu )$ -solvable, then it is $\mu $ -superstable.

2. 2. [18, Corollary 5.5] If $\mu $ is high enough and $\mathbf {K}$ is $\mu $ -superstable, then there is some $\lambda \geq \mu $ and some $\lambda '<\lambda $ such that $\mathbf {K}$ is $(\lambda ,\lambda ')$ -solvable.

3. 3. (Proposition 6.24) If $\mathbf {K}$ has continuity of $\mu $ -nonsplitting, then it is $\mu $ -superstable iff it is $(\mu ^+,\mu ^+)$ -solvable.

In Section 7, we will consider two characterizations of superstability: stability in a tail and the boundedness of the U-rank. Vasey [38, Corollary 4.24] showed that stability in a tail is also an equivalent definition of superstability, but the starting cardinal of superstability $(\lambda '(\mathbf {K}))^++\chi _1$ is only bounded above by the Hanf number of $\mu $ (he also implicitly assumed continuity of nonsplitting in deriving his results). In contrast, we carry out a slightly different proof to obtain $\mu ^{ }$ -superstability, assuming stability in unboundedly many cardinals below $\mu ^{ }$ , and enough stability above $\mu $ .

Theorem 1.5. Let $\mu>\operatorname {LS}(\mathbf {K})$ with cofinality ${\aleph _0}$ , $\mathbf {K}$ have a monster model, have continuity of nonsplitting, be $\mu $ -tame, stable in both $\mu $ and unboundedly many cardinals below $\mu $ .

1. 1. [38, Corollary 4.14] If $\mu \geq (\lambda '(\mathbf {K}))^++\chi _1$ , then $ \mathbf {K}$ is $\mu $ -superstable.

2. 2. (Proposition 7.5) There is $\lambda <h(\mu )$ such that if $\mathbf {K}$ is stable in $[\mu ,\lambda )$ , then it is $\mu $ -superstable.

It was mentioned at the end of [18] that the no tree property and the boundedness of a rank function could be generalized to AECs. Some partial answers were given in [15] regarding the no tree property (assuming a simple independence relation). Here we prove that the boundedness of the U-rank (with respect to $\mu $ -nonforking for limit models in $K_{\mu }$ ordered by universal extensions) is equivalent to $\mu $ -superstability (Corollary 7.14). We will need to extend our nonforking to longer types, using results from [12]. Then we can quote a lot of known results from [6, 7, 15]. Our strategy of extending frames contrasts with [32] which used a complicated axiomatic framework and drew technical results from [24, III]. Here we directly construct a type-full good $\mu $ -frame from nonforking and the known results apply (which are independent of the technical ones in [24, 32]).

Theorem 1.6. Let $\mu \geq \operatorname {LS}(\mathbf {K})$ be regular, $\mathbf {K}$ have a monster model, be $\mu $ -tame, stable in $\mu $ and have continuity of $\mu $ -nonsplitting. Let $U(\cdot )$ be the U-rank induced by $\mu $ -nonforking restricted to limit models in $K_{\mu }$ ordered by $\leq _u$ . The following are equivalent:

1. 1. $\mathbf {K}$ is $\mu $ -superstable.

2. 2. $U(p)<\infty $ for all $p\in \operatorname {gS}(M)$ and limit model $M\in K_{\mu }$ .

In Section 8, we summarize all our results as two main theorems: one for the superstable case and one for the strictly stable case. We give two applications in algebra: those results were known but here we only rely on model-theoretic techniques.

2 Preliminaries

Throughout this paper, we assume the following:

Assumption 2.1.

1. 1. $\mathbf {K}$ is an AEC with $AP$ , $JEP,$ and $NMM$ .

2. 2. $\mathbf {K}$ is stable in some $\mu \geq \operatorname {LS}(\mathbf {K})$ .

3. 3. $\mathbf {K}$ is $\mu $ -tame.

4. 4. $\mathbf {K}$ satisfies continuity of $\mu $ -nonsplitting (Definition 3.5).

5. 5. $\chi \leq \mu $ where $\chi $ is the minimum local character cardinal of $\mu $ -nonsplitting (see Definition 3.10).

$AP$ stands for amalgamation property, $JEP$ for joint embedding property, and $NMM$ for no maximal model. They allow the construction of a monster model. Given a model $M\in K$ , we write $\operatorname {gS}(M)$ the set of Galois types over M (the ambient model does not matter because of $AP$ ).

Definition 2.2. Let $\lambda $ be an infinite cardinal.

1. 1. $\alpha \geq 2$ be an ordinal, $\mathbf {K}$ is $(<\alpha )$ -stable in $\lambda $ if for any $\Vert M \Vert =\lambda $ , $|\operatorname {gS}^{<\alpha }(M)|\leq \lambda $ . We omit $\alpha $ if $\alpha =2$ .

2. 2. $\mathbf {K}$ is $\lambda $ -tame if for any $N\in K$ , any $p\neq q\in \operatorname {gS}(N)$ , there is $M\leq N$ of size $\lambda $ such that $p\restriction M\neq q\restriction M$ .

Definition 2.3. Let $\lambda \geq \operatorname {LS}(\mathbf {K})$ be a cardinal and $\alpha ,\beta <\lambda ^+$ be regular. Let $M\leq N$ and $\Vert M \Vert =\lambda $ .

1. 1. N is universal over M ( $M<_uN$ ) if $M<N$ and for any $\Vert N' \Vert =\Vert N \Vert $ , there is $f:N'\xrightarrow [M]{}N$ .

2. 2. N is $(\lambda ,\alpha )$ -limit over M if $\Vert N \Vert =\lambda $ and there exists $\langle M_i:i\leq \alpha \rangle \subseteq K_\lambda $ increasing and continuous such that $M_0=M$ , $M_\alpha =N$ and $M_{i+1}$ is universal over $M_i$ for $i<\alpha $ . We call $\alpha $ the length of N.

3. 3. N is $(\lambda ,\alpha )$ -limit if there exists $\Vert M' \Vert =\lambda $ such that N is $(\lambda ,\alpha )$ -limit over $M'$ .

4. 4. N is $(\lambda ,\geq \beta )$ -limit (over M) if there exists $\alpha \geq \beta $ such that (2) (resp. (3)) holds.

5. 5. N is $(\lambda ,\lambda ^+)$ -limit (over M) if $\Vert N \Vert =\lambda ^+$ and we replace $\alpha $ by $\lambda ^+$ in (2) (resp. (3)).

6. 6. Let $\lambda _1\leq \lambda _2$ , then N is $([\lambda _1,\lambda _2],\geq \beta )$ -limit (over M) if there exists $\lambda \in [\lambda _1,\lambda _2]$ such that N is $(\lambda ,\geq \beta )$ -limit (over M).

7. 7. If $\lambda>\operatorname {LS}(\mathbf {K})$ , we say M is $\lambda $ -saturated if for any $M'\leq M$ , $\Vert M' \Vert <\lambda $ , $M\vDash \operatorname {gS}(M')$ .

8. 8. M is saturated if it is $\Vert M \Vert $ -saturated.

In general, we do not know limit models or saturated models are closed under chains, so they do not necessary form an AEC. We adapt [32, Definition 5.3] to capture such behaviours.

Definition 2.4. An abstract class $\mathbf {K}_{\mathbf {1}}$ is a $\mu $ -skeleton of $\mathbf {K}$ if the following is satisfied:

1. 1. $\mathbf {K}_{\mathbf {1}}$ is a sub-AC of $\mathbf {K}_{\boldsymbol {\mu }}$ : $K_1\subseteq K_{\mu }$ and for any $M,N\in K_1$ , $M\leq _{\mathbf {K}_{\mathbf {1}}} N$ implies $M\leq _{\mathbf {K}} N$ .

2. 2. For any $M\in K_{\mu }$ , there is $M'\in K_1$ such that $M\leq _{\mathbf {K}} M'$ .

3. 3. Let $\alpha $ be an ordinal and $\langle M_i:i<\alpha \rangle $ be $\leq _{\mathbf {K}}$ -increasing in $K_1$ . There exists $N\in K_1$ such that for all $i<\alpha $ , $M_i\leq _{\mathbf {K}_{\mathbf {1}}} N$ (the original definition requires strict inequality but it is immaterial under $NMM$ ).

We say $\mathbf {K}_{\mathbf {1}}$ is a $(\geq \mu )$ -skeleton of $\mathbf {K}$ if the above items hold for $K_{\geq \mu }$ in place of $K_{\mu }$ .

By [24, II Claim 1.16], limit models in $\mu $ with $\leq _{\mathbf {K}}$ form a $\mu $ -skeleton of $\mathbf {K}$ . Similarly let $\alpha <\mu ^+$ be regular, then $(\geq \mu ,\geq \alpha )$ -limits form a $(\geq \mu )$ -skeleton of $\mathbf {K}$ .

On the other hand, good frames were developed by Shelah [24] for AECs in a range of cardinals. Vasey [32] defined good frames over a coherent abstract class. We specialize the abstract class to a skeleton of an AEC.

Definition 2.5. Let $\mathbf {K}$ be an AEC, and let $\mathbf {K}_{\mathbf {1}}$ be a $\mu $ -skeleton of $\mathbf {K}$ . We say a nonforking relation is a good $\mu $ -frame over the skeleton of $\mathbf {K}_{\mathbf {1}}$ if the following holds:

1. 1. The nonforking relation is a binary relation between a type $p\in \operatorname {gS}(N)$ and a model $M\leq _{\mathbf {K}_{\mathbf {1}}}N$ . We say p does not fork over M if the relation holds between p and M. Otherwise we say p forks over M.

2. 2. Invariance: if $f\in \operatorname {Aut}(\mathfrak {C})$ and p does not fork over M, then $f(p)$ does not fork over $f[M]$ .

3. 3. Monotonicity: if $p\in \operatorname {gS}(N)$ does not fork over M and $M\leq _{\mathbf {K}_{\mathbf {1}}}M'\leq _{\mathbf {K}_{\mathbf {1}}} N$ for some $M'\in K_1$ , then $p\restriction M'$ does not fork over M while p itself does not fork over $M'$ .

4. 4. Existence: if $M\in K_1$ and $p\in \operatorname {gS}(M)$ , then p does not fork over M.

5. 5. Extension: if $M\leq _{\mathbf {K}_{\mathbf {1}}}N\leq _{\mathbf {K}_{\mathbf {1}}}N'$ and $p\in \operatorname {gS}(N)$ does not fork over M, then there is $q\in \operatorname {gS}(N')$ such that $q\supseteq p$ and q does not fork over M.

6. 6. Uniqueness: if $p,q\in \operatorname {gS}(N)$ do not fork over M and $p\restriction M=q\restriction M$ , then $p=q$ .

7. 7. Transitivity: if $M_0\leq _{\mathbf {K}_{\mathbf {1}}}M_1\leq _{\mathbf {K}_{\mathbf {1}}}M_2$ , $p\in \operatorname {gS}(M_2)$ does not fork over $M_1$ , $p\restriction M_1$ does not fork over $M_0$ , then p does not fork over $M_0$ .

8. 8. Local character ${\aleph _0}$ : if $\delta $ is an ordinal of cofinality $\geq {\aleph _0}$ , $\langle M_i:i\leq \delta \rangle $ is $\leq _{\mathbf {K}_{\mathbf {1}}}$ -increasing and continuous, then there is $i<\delta $ such that p does not fork over $M_i$ .

9. 9. Continuity: Let $\delta $ is a limit ordinal and $\langle M_i:i\leq \delta \rangle $ be $\leq _{\mathbf {K}_{\mathbf {1}}}$ -increasing and continuous. If for all $1\leq i<\delta $ , $p_i\in \operatorname {gS}(M_i)$ does not fork over $M_0$ and $p_{i+1}\supseteq p_i$ , then $p_\delta $ does not fork over $M_0$ .

10. 10. Symmetry: let $M\leq _{\mathbf {K}_{\mathbf {1}}}N$ , $b\in |N|$ , $\operatorname {gtp}(b/M)$ do not fork over M, $\operatorname {gtp}(a/N)$ do not fork over M. There is $N_a\geq _{\mathbf {K}_{\mathbf {1}}}M$ such that $\operatorname {gtp}(b/N_a)$ do not fork over M.

If the above holds for a $(\geq \mu )$ -skeleton $\mathbf {K}_{\mathbf {1}}$ , then we say the nonforking relation is a good $(\geq \mu )$ -frame over the skeleton $\mathbf {K}_{\mathbf {1}}$ . If $\mathbf {K}_{\mathbf {1}}$ is itself an AEC (in $\mu $ ), then we omit “skeleton.” Let $\alpha <\mu ^+$ be regular. We say a nonforking relation has local character $\alpha $ if we replace “ ${\aleph _0}$ ” in item (8) by $\alpha $ .

Remark 2.6.

1. 1. In this paper, $\mathbf {K}_{\mathbf {1}}$ will be the $(\mu ,\geq \alpha )$ -limit models for some $\alpha <\mu ^+$ , with $\leq _{\mathbf {K}_{\mathbf {1}}}=\leq _u$ (the latter is in $\mathbf {K})$ .

2. 2. In Fact 7.20, we will draw results of a good frame over longer types, where we allow the types in the above definition to be of arbitrary length. Extension property will have an extra clause that allows extension of a shorter type to a longer one that still does not fork over the same base.

3. 3. Some of the properties of a good frame imply or simply one another. Instead of using a minimalistic formulation (for example, in [37, Definition 17.1]), we keep all the properties because sometimes it is easier to deduce a certain property first.

3 Properties of nonsplitting

Let $p\in \operatorname {gS}(N)$ , $f:N\rightarrow N'$ , we write $f(p):=\operatorname {gtp}(f^+(d)/f(N))$ where $f^+$ extends f to include some $d\vDash p$ in its domain.

Proposition 3.1. Such $f^+$ exists by $AP$ and $f(p)$ is independent of the choice of $f^+$ .

Proof Pick $a\in N_1\geq $ realizing p, use $AP$ to obtain $f_1^+:a\mapsto c$ extending f (enlarge $N_1$ if necessary so that $f_1^+(N_1)$ contains $f(N)$ ).

Suppose $b\in N_2$ realizes p and there is $f_2^+:b\mapsto d$ extending f. Extend $N_2$ so that $f_2^+$ is an isomorphism. We need to find $h:d\mapsto c$ which fixes $f(N)$ . Since $a,b\vDash p$ , by $AP$ there is $N_3\ni b$ and $g:N_1\xrightarrow [N]{}N_3$ that maps a to b. Extend g to an isomorphism $N_1'\cong _N N_3\geq N_2$ . By $AP$ again, obtain $f_1^{++}$ of domain $N_1'$ extending $f_1^+$ . Therefore, $d\in f(N_2^+)$ and $f_1^{++}\circ g^{-1}\circ \operatorname {id}_{N_2}\circ (f_2^+)^{-1}(d)=c$ . Hence we can take $h:= f_1^{++}\circ g^{-1}\circ \operatorname {id}_{N_2}\circ (f_2^+)^{-1}:f_2^+(N_2)\xrightarrow [f(N)]{}f_1^{++}(N_1') $ .

Definition 3.2. Let $M,N\in K$ , $p\in \operatorname {gS}(N)$ . $p \ \mu $ -splits over M if there exists $N_1,N_2$ of size $\mu $ such that $M\leq N_1,N_2\leq N$ and $f:N_1\xrightarrow [M]{}N_2$ such that $f(p)\restriction N_2\neq p\restriction N_2$ .

Proposition 3.3 (Monotonicity of nonsplitting).

Let $M,N\in K_{\mu }$ , $p\in \operatorname {gS}(N)$ do not $\mu $ -split over M. For any $M_1,N_1$ with $M\leq M_1\leq N_1\leq N$ , we have $p\restriction N_1$ does not $\mu $ -split over $M_1$ .

Proposition 3.4. Let $M,N\in K$ , $M\in K_{\mu }$ and $p\in \operatorname {gS}(N)$ . $p \ 5\mu $ -splits over M iff $p \ (\geq \mu )$ -splits over M (the witnesses $N_1,N_2$ can be in $K_{\geq \mu }$ ).

Proof We sketch the backward direction: pick $N_1,N_2\in K_{\geq \mu }$ witnessing $p \ (\geq \mu )$ -splits over M. By $\mu $ -tameness and Löwenheim–Skolem axiom, we may assume $N_1,N_2\in K_{\mu }$ .

Definition 3.5. Let $\chi $ be a regular cardinal.

1. 1. A chain $\langle M_i:i\leq \delta \rangle $ is u-increasing if $M_{i+1}>_uM_i$ for all $i<\delta $ .

2. 2. $\mathbf {K}$ satisfies continuity of $\mu $ -nonsplitting if for any limit ordinal $\delta $ , $\langle M_i:i\leq \delta \rangle \subseteq K_{\mu }$ u-increasing and continuous, $p\in \operatorname {gS}(M_\delta )$ ,

   $$ \begin{align*} p\restriction M_i \text{ does not } \mu\text{-split over } M_0 \text{ for } i < \delta \Rightarrow p \text{ does not } \mu\text{-split over } M_0. \end{align*} $$

3. 3. $\mathbf {K}$ has $\chi $ -weak local character of $\mu $ -nonsplitting if for any limit ordinal $\delta \geq \chi $ , $\langle M_i:i\leq \delta \rangle \subseteq K_{\mu }$ u-increasing and continuous, $p\in \operatorname {gS}(M_\delta )$ , there is $i<\delta $ such that $p\restriction M_{i+1}$ does not $\mu $ -split over $M_i$ .

4. 4. $\mathbf {K}$ has $\chi $ -local character of $\mu $ -nonsplitting if the conclusion in (3) becomes: p does not $\mu $ -split over $M_i$ .

We call any $\delta $ that satisfies (3) or (4) a (weak) local character cardinal.

Remark 3.6. When defining the continuity of nonsplitting, we can weaken the statement by removing the assumption that p exists and replacing $p\restriction M_i$ by $p_i$ increasing. This is because we can use [4, Proposition 5.2] to recover p. In details, we can use the weaker version of continuity and weak uniqueness (Proposition 3.12) to argue that the $p_i$ ’s form a coherent sequence. p can be defined as the direct limit of the $p_i$ ’s.

The following lemma connects the three properties of $\mu $ -nonsplitting:

Lemma 3.7 [9, Lemma 11(1)].

If $\mu $ is regular, $\mathbf {K}$ satisfies continuity of $\mu $ -nonsplitting and has $\chi $ -weak local character of $\mu $ -nonsplitting, then it has $\chi $ -local character of $\mu $ -nonsplitting.

Proof Let $\delta $ be a limit ordinal of cofinality $\geq \chi $ , $\langle M_i:i\leq \delta \rangle $ u-increasing and continuous. Suppose $p\in \operatorname {gS}(M_\delta )$ splits over $M_i$ for all $i<\delta $ . Define $i_0:=0$ . By $\delta $ regular and continuity of $\mu $ -nonsplitting, build an increasing and continuous sequence of indices $\langle i_k:k<\delta \rangle $ such that $p\restriction M_{i_{k+1}} \ \mu $ -splits over $M_{i_k}$ . Notice that $M_{i_{k+1}}>_uM_{i_k}$ . Then applying $\chi $ -weak local character to $\langle M_{i_k}:k<\delta \rangle $ yields a contradiction.

From stability (even without continuity of nonsplitting), it is always possible to obtain weak local character of nonsplitting. Shelah sketched the proof and alluded to the first-order analog, so we give details here.

Lemma 3.8 [23, Claim 3.3(2)].

If $\mathbf {K}$ is stable in $\mu $ (which is in Assumption 2.1), then for some $\chi \leq \mu $ , it has weak $\chi $ -local character of $\mu $ -nonsplitting.

Proof Pick $\chi \leq \mu $ minimum such that $2^{\chi }>\mu $ . Suppose we have $\langle M_i:i\leq \chi \rangle $ u-increasing and continuous and $d\vDash p\in \operatorname {gS}(M_\chi )$ such that for all $i<\chi $ , $p\restriction M_{i+1} \ \mu $ -splits over $p\restriction M_i$ . Then for $i<\chi $ , we have $N_i^1$ and $N_i^2$ of size $\mu $ , $M_i\leq N_i^1,N_i^2\leq M_{i+1}$ , $f_i:N_i^1\cong _{M_i}N_i^2$ and $f_i(p)\restriction N_i^2\neq p\restriction N_i^2$ . We build $\langle M_i':i\leq \chi \rangle $ and $\langle h_\eta :M_{l(\eta )}\xrightarrow [M_0]{}M_{l(\eta )}'\,|\,\eta \in 2^{\leq \chi }\rangle $ both increasing and continuous with the following requirements:

1. 1. $h_{\langle \rangle }:=\operatorname {id}_{M_0}$ and $M_0':= M_0$ .

2. 2. For $\eta \in 2^{<\chi }$ , $h_{\eta ^\frown 0}\restriction N_{l(\eta )}^2=h_{\eta ^\frown 1}\restriction N_{l(\eta )}^2$ .

We specify the successor step: suppose $l(\nu )=i$ and $h_\nu $ has been constructed. By $AP$ , obtain:

1. 1. $h:N_i^2\rightarrow M^*\geq M_i'$ with $h\supseteq h_\nu $ .

2. 2. $h_{\nu ^\frown 0}:M_{i+1}\rightarrow M^{**}\geq M^*$ with $h_{\nu ^\frown 0}\supseteq h$ .

3. 3. $g_0:M_{i+1}\rightarrow M_{hf_i}\geq M^*$ with $g_0\supseteq h\circ f_i$ .

4. 4. $g_1:M_{hf_i}\rightarrow M_{i+1}'\geq M^{**}$ with $g_1\circ g_0=h_{\nu ^\frown 0}$ .

Define $h_{\nu ^\frown 1}:= g_1\circ g_0:M_{i+1}\rightarrow M_{i+1}'$ . By diagram chasing, $h_{\nu ^\frown 1}\restriction M_i=g_1\circ g_0\restriction M_i=g_1\circ h\circ f_i\restriction M_i=g_1\circ h\restriction M_i=h\restriction M_i=h_\nu \restriction M_i$ . On the other hand, $h_{\nu ^\frown 0}\restriction M_i=h\restriction M_i=h_\nu \restriction M_i$ . Therefore the maps are increasing. Now $h_{\nu ^\frown 1}\restriction N_i^2=g_1\circ g_0\restriction N_i^2=h_{\nu ^\frown 0}\restriction N_i^2$ by item (4) in our construction.

For $\eta \in 2^{\chi }$ , extend $h_\eta $ so that its range includes $M_\chi '$ and its domain includes d. We show that $\{\operatorname {gtp}(h_\eta (d)/M_{\chi }'):\eta \in 2^{\chi }\}$ are pairwise distinct. For any $\eta \neq \nu \in 2^{\chi }$ , pick the minimum $i<\chi $ such that $\eta [i]\neq \nu [i]$ . Without loss of generality, assume $\eta [i]=0$ , $\nu [i]=1$ . Using the diagram above (see the comment before Proposition 3.1),

$$ \begin{align*} \operatorname{gtp}(h_\eta(d)/M_{\chi}')&\supseteq\operatorname{gtp}(h_{\eta}(d)/h(N_i^2))\\ &=h(\operatorname{gtp}(d/N_i^2))\\ &\neq h\circ f_i(\operatorname{gtp}(d/N_i^1))\\ &=g_1\circ h\circ f_i(\operatorname{gtp}(d/N_i^1))\\ &\subseteq\operatorname{gtp}(h_\nu(d)/M_{\chi}'). \end{align*} $$

This contradicts the stability in $\mu $ .

Proposition 3.9. If $\mu $ is regular, then for some $\chi \leq \mu $ , $\mathbf {K}$ has the $\chi $ -local character of $\mu $ -nonsplitting.

Proof By Lemma 3.8 and uniqueness of limit models of the same cofinality, $\mathbf {K}$ has $\mu $ -weak local character of $\mu $ -nonsplitting. By Lemma 3.7 (together with continuity of $\mu $ -nonsplitting in Assumption 2.1), $\mathbf {K}$ has $\mu $ -local character of $\mu $ -nonsplitting. Hence $\chi $ exists and $\chi \leq \mu $ .

From now on, we fix the following.

Definition 3.10. $\chi $ is the minimum local character cardinal of $\mu $ -nonsplitting. $\chi \leq \mu $ if either $\mu $ is regular (by the previous proposition), or $\mu $ is greater than some regular stability cardinal $\xi $ where $\mathbf {K}$ has continuity of $\xi $ -nonsplitting and is $\xi $ -tame (by Lemma 6.7).

Remark 3.11. Without continuity of nonsplitting, it is not clear whether there can be gaps between the local character cardinals: Definition 3.5(4) might hold for $\delta =\aleph _0$ and $\delta =\aleph _2$ but not $\delta =\aleph _1$ . In that case defining $\chi $ as the minimum local character cardinal might not be useful. Similar obstacles form when we only know a particular $\lambda $ is a local character cardinal but not necessary those above $\lambda $ .

Meanwhile, weak local character cardinals close upwards and we can eliminate the above situation by assuming continuity of nonsplitting: if we know $\chi $ is the minimum local character cardinal, then it is also a weak local character cardinal, so are all regular cardinals between $[\chi ,\mu ^+)$ . By the proof of Lemma 3.7, the regular cardinals between $[\chi ,\mu ^+)$ are all local character cardinals.

We now state the existence, extension, weak uniqueness, and weak transitivity properties of $\mu $ -nonsplitting. The original proof for weak uniqueness assumes $\Vert M \Vert =\mu $ but it is not necessary; while that for extension and for weak transitivity assume all models are in $K_{\mu }$ ; but under tameness we can just require $\Vert M \Vert =\Vert N \Vert $ .

Proposition 3.12. Let $M_0<_u M\leq N$ where $\Vert M_0 \Vert =\mu $ .

1. 1. [23, Claim 3.3(1)] (Existence) If $p\in \operatorname {gS}(N)$ , there is $N_0\leq N$ of size $\mu $ such that p does not $\mu $ -split over $N_0$ .

2. 2. [16, Theorem 6.2] (Weak uniqueness) If $p,q\in \operatorname {gS}(N)$ both do not $\mu $ -split over $M_0$ , and $p\restriction M=q\restriction M$ , then $p=q$ .

3. 3. [16, Theorem 6.1] (Extension) Suppose $\Vert M \Vert =\Vert N \Vert $ . For any $p\in \operatorname {gS}(M)$ that does not $\mu $ -split over $M_0$ , there is $q\in \operatorname {gS}(N)$ extending p such that q does not $\mu $ -split over $M_0$ .

4. 4. [33, Proposition 3.7] (Weak transitivity) Suppose $\Vert M \Vert =\Vert N \Vert $ . Let $M^*\leq M_0$ and $p\in \operatorname {gS}(N)$ . If p does not $\mu $ -split over $M_0$ while $p\restriction M$ does not $\mu $ -split over $M^*$ , then p does not $\mu $ -split over $M^*$ .

Proof

1. 1. We skip the proof, which has the same spirit as that of Lemma 3.8.

2. 2. By stability in $\mu $ , we may assume that $\Vert M \Vert =\mu $ . Suppose $p\neq q$ , by tameness in $\mu $ we may find $M'\in K_{\mu }$ such that $M\leq M'\leq N$ and $p\restriction M'\neq q\restriction M'$ . By $M_0<_uM$ and $M_0<N$ , we can find $f:M'\xrightarrow [M_0]{}M$ . Using nonsplitting twice, we have $p\restriction f(M')=f(p)$ and $q\restriction M'=f(q)$ . But $f(M')\leq M$ implies $p\restriction f(M')=q\restriction f(M')$ . Hence $f(p)=f(q)$ and $p=q$ .

3. 3. By universality of M, find $f:N\xrightarrow [M_0]{}M$ . We can set $q:= f^{-1}(p\restriction f(N))$ .

4. 4. Let $q:= p\restriction M$ . By extension, obtain $q'\supseteq q$ in $\operatorname {gS}(N)$ such that $q'$ does not $\mu $ -split over $M^*$ . Now $p\restriction M=q\restriction M=q'\restriction M$ and both $p,q'$ do not $\mu $ -split over $M_0$ (for $q'$ use monotonicity, see Proposition 3.3). By weak uniqueness, $p=q'$ and the latter does not $\mu $ -split over $M^*$ .

Transitivity does not hold in general for $\mu $ -nonsplitting. The following example is sketched in [2, Example 19.3].

Example 3.13. Let T be the first-order theory of a single equivalence relation E with infinitely many equivalence classes and each class is infinite. Let $M\leq N$ where N contains (representatives of) two more classes than M. Let d be an element. Then $\operatorname {\mathrm {tp}}(d/N)$ splits over M iff $dEa$ for some element $a\in N$ but $\neg dEb$ for any $b\in M$ . Meanwhile, suppose $M_0\leq M$ both of size $\mu $ , then $M_0<_u M$ iff M contains $\mu $ -many new classes and each class extends $\mu $ many elements. Now require $M_0<_u M$ while N contains only an extra class than M, say witnessed by d, then $\operatorname {\mathrm {tp}}(d/N)$ cannot split over M. Also $\operatorname {\mathrm {tp}}(d/M)$ does not split over $M_0$ because d is not equivalent to any elements from M. Finally $\operatorname {\mathrm {tp}}(d/N)$ splits over $M_0$ because it contains two more classes than $M_0$ (one must be from M).

The same argument does not work if also $M<_u N$ because N would contain two more classes than M and they will witness $\operatorname {\mathrm {tp}}(d/N)$ splits over M. Baldwin originally assigned it as [2, Exercise 12.9] but later [3] retracted the claim.

Question 3.14. When models are ordered by $\leq _u$ :

1. 1. Does uniqueness of $\mu $ -nonsplitting hold? Namely, let $M<_uN$ both in $K_{\mu }$ , $p,q\in \operatorname {gS}(N)$ both do not $\mu $ -split over M, $p\restriction M=q\restriction M$ , then $p=q$ .

2. 2. Does transitivity of $\mu $ -nonsplitting hold? Namely, let $M_0<_uM<_uN$ all in $K_{\mu }$ , $p\in \operatorname {gS}(N)$ does not $\mu $ -split over M and $p\restriction M$ does not $\mu $ -split over $M_0$ , then p does not $\mu $ -split over $M_0$ .

In Assumption 2.1, we assumed continuity of $\mu $ -nonsplitting. One way to obtain it is to assume superstability which is stronger. Another way is to assume $\omega $ -type locality.

Definition 3.15.

1. 1. [14, Definition 7.12] Let $\lambda \geq \operatorname {LS}(\mathbf {K})$ , $\mathbf {K}$ is $\lambda $ -superstable if it is stable in $\lambda $ and has ${\aleph _0}$ -local character of $\lambda $ -nonsplitting.

2. 2. [2, Definition 11.4] Types in $\mathbf {K}$ are $\omega $ -local if: for any limit ordinal $\alpha $ , $\langle M_i:i\leq \alpha \rangle $ increasing and continuous, $p,q\in \operatorname {gS}(M)$ and $p\restriction M_i=q\restriction M_i$ for all $i<\alpha $ , then $p=q$ .

Proposition 3.16. Let $\mathbf {K}$ satisfy Assumption 2.1 except for the continuity of $\mu $ -nonsplitting. It will satisfy the continuity of $\mu $ -nonsplitting if either:

1. 1. $\mathbf {K}$ is $\mu $ -superstable; or

2. 2. types in $\mathbf {K}$ are $\omega $ -local.

Proof For (1), it suffices to prove that for any regular $\lambda \geq {\aleph _0}$ , $\lambda $ -local character implies continuity of $\mu $ -nonsplitting over chains of cofinality $\geq \lambda $ . Let $\langle M_i:i\leq \lambda \rangle $ be u-increasing and continuous. Suppose $p\in \operatorname {gS}(M_\lambda )$ satisfies $p\restriction M_i$ does not $\mu $ -split over $M_0$ for all $i<\lambda $ . By $\lambda $ -local character, p does not $\mu $ -split over some $M_i$ . If $i=0$ we are done. Otherwise, we have $M_0<_uM_i<_uM_{i+1}<_uM_\lambda $ . By assumption, $p\restriction M_{i+1}$ does not $\mu $ -split over $M_0$ . By weak transitivity (Proposition 3.12), p does not $\mu $ -split over $M_0$ as desired.

For (2), let $\langle M_i:i\leq \lambda \rangle $ and p as above. By assumption $p\restriction M_1$ does not $\mu $ -split over $M_0$ and $M_1>_uM_0$ . By extension (Proposition 3.12), there is $q\supseteq p\restriction M_1$ in $\operatorname {gS}(M_\lambda )$ such that q does not $\mu $ -split over $M_0$ . By monotonicity, for $2\leq i<\lambda $ , $q\restriction M_i$ does not $\mu $ -split over $M_0$ . Now $(q\restriction M_i)\restriction M_1=p\restriction M_1=(p\restriction M_i)\restriction M_1$ , we can use weak uniqueness (Proposition 3.12) to inductively show that $q\restriction M_i=p\restriction M_i$ for all $i<\lambda $ . By $\omega $ -locality, $p=q$ and the latter does not $\mu $ -split over $M_0$ as desired.

Once we have continuity of $\mu $ -nonsplitting in $K_{\mu }$ , it automatically works for $K_{\geq \mu }$ .

Proposition 3.17. Let $\delta $ be a limit ordinal, $\langle M_i:i\leq \delta \rangle \subseteq K_{\geq \mu }$ be u-increasing and continuous, $p\in \operatorname {gS}(M_\delta )$ . If for all $i<\delta $ , $p\restriction M_i$ does not $\mu $ -split over $M_0$ , then p also does not $\mu $ -split over $M_0$ .

Proof The statement is vacuous when $M_0\in K_{>\mu }$ so we assume $M_0\in K_{\mu }$ . By cofinality argument we may also assume $\operatorname {cf}(\delta )\leq \mu $ . Suppose $p \ \mu $ -splits over $M_0$ and pick witnesses $N^a$ and $N^b$ of size $\mu $ . Using stability, define another u-increasing and continuous chain $\langle N_i:i\leq \delta \rangle \subseteq K_{\mu }$ such that:

1. 1. For $i\leq \delta $ , $N_i\leq M_i$ .

2. 2. $N_\delta $ contains $N^a$ and $N^b$ .

3. 3. $N_0:= M_0$ .

4. 4. For $i\leq \delta $ , $|N_i|\supseteq |M_i|\cap (|N^a|\cup |N^b|)$ .

By assumption each $p\restriction M_i$ does not $\mu $ -split over $M_0$ , so by monotonicity $p\restriction N_i$ does not $\mu $ -split over $N_0=M_0$ . By continuity of $\mu $ -nonsplitting, $p\restriction N_\delta $ does not $\mu $ -split over $N_0$ , contradicting item (2) above.

4 Good frame over $(\geq \chi )$ -limit models except symmetry

As seen in Proposition 3.12, $\mu $ -nonsplitting only satisfies weak transitivity but not transitivity, which is a key property of a good frame. We will adapt [33, Definitions 3.8 and 4.2] to define nonforking from nonsplitting to solve this problem.

Definition 4.1. Let $M\leq N$ in $K_{\geq \mu }$ and $p\in \operatorname {gS}(N)$ .

1. 1. p (explicitly) does not $\mu $ -fork over $(M_0,M)$ if $M_0\in K_{\mu }$ , $M_0<_uM$ and p does not $\mu $ -split over $M_0$ .

2. 2. p does not $\mu $ -fork over M if there exists $M_0$ satisfying (1).

We call $M_0$ the witness to $\mu $ -nonforking over M.

The main difficulty of the above definition is that different $\mu $ -nonforkings over M may have different witnesses. For extension, the original approach in [33] was to work in $\mu ^+$ -saturated models. Later [31, Proposition 5.1] replaced it by superstability in an interval, which works for $K_{\geq \mu }$ . We weaken the assumption to stability in an interval and continuity of $\mu $ -nonsplitting, and use a direct limit argument similar to that of [4, Theorem 5.3].

Proposition 4.2 (Extension).

Let $M\leq N\leq N'$ in $K_{\geq \mu }$ . If $\mathbf {K}$ is stable in $[\Vert N \Vert ,\Vert N' \Vert ]$ and $p\in \operatorname {gS}(N)$ does not $\mu $ -fork over M, then there is $q\supseteq p$ in $\operatorname {gS}(N')$ such that q does not $\mu $ -fork over M.

Proof Since p does not $\mu $ -fork over M, we can find witness $M_0\in K_{\mu }$ such that $M_0<_uM$ and p does not $\mu $ -split over $M_0$ . If $\Vert N \Vert =\Vert N' \Vert $ , we can use extension of nonsplitting (Proposition 3.12) to obtain (the unique) $q\in \operatorname {gS}(N')$ extending p which does not $\mu $ -split over $M_0$ . By definition q does not $\mu $ -fork over M.

If $\Vert N \Vert {\kern-1.5pt}<{\kern-1.5pt}\Vert N' \Vert $ , first we assume $N<_uN'$ and resolve $N'{\kern-1.5pt}={\kern-1.5pt}\bigcup \{N_i:i{\kern-1.5pt}\leq{\kern-1.5pt} \alpha +1\}$ u-increasing and continuous where $N_0=N$ , $\Vert N_{\alpha } \Vert =\Vert N' \Vert $ , $N_{\alpha +1}=N'$ . The construction is possible by stability in $[\Vert N \Vert ,\Vert N' \Vert ]$ . We will define a coherent sequence $\langle p_i:i\leq \alpha \rangle $ such that $p_i$ is a nonsplitting extension of p in $\operatorname {gS}(N_i)$ . The first paragraph gives the successor step. For limit step $\delta \leq \alpha $ , we take the direct limit to obtain an extension $p_\delta $ of $\langle p_i:i<\delta \rangle $ . Since all previous $p_i$ does not $\mu $ -split over $M_0$ , by Proposition 3.17, $p_\delta $ also does not $\mu $ -split over $M_0$ . After the construction has finished, we obtain $q:= p_{\alpha }$ a nonsplitting extension of p in $\operatorname {gS}(N')$ . Since $M_0<_uM\leq N'$ , we still have q does not $\mu $ -fork over M.

In the general case where $N\leq N'$ , extend $N'<_u N"$ with $\Vert N" \Vert =\Vert N' \Vert $ . Then we can extend p to a nonforking $q"\in \operatorname {gS}(N")$ and use monotonicity to obtain the desired q.

Corollary 4.3. Let $M_0<_u M\leq N'$ with $M_0\in K_{\mu }$ . If $\mathbf {K}$ is stable in $[\Vert M \Vert ,\Vert N' \Vert ]$ and $p\in \operatorname {gS}(M)$ does not $\mu $ -split over $M_0$ , then there is $q\supseteq p$ in $\operatorname {gS}(N')$ such that q does not $\mu $ -split over $M_0$ .

Proof Run through the exact same proof as in Proposition 4.2, where $M=N$ and $M_0$ is given in the hypothesis.

For continuity, the original approach in [33, Lemma 4.12] was to deduce it from superstability (which we do not assume) and transitivity. Transitivity there was obtained from extension and uniqueness, and uniqueness was proved in [33, Lemma 5.3] for $\mu ^+$ -saturated models only (or assuming superstability in [35, Lemma 2.12]). Our new argument uses weak transitivity and continuity of $\mu $ -nonsplitting to show that continuity of $\mu $ -nonforking holds for a universally increasing chain in $K_{\mu }$ . The case in $K_{\geq \mu }$ will be proved after we have developed transitivity and local character of nonforking.

Proposition 4.4 (Continuity 1).

Let $\delta <\mu ^+$ be a limit ordinal and $\langle M_i:i\leq \delta \rangle \subseteq K_{\mu }$ be u-increasing and continuous. Let $p\in \operatorname {gS}(M_\delta )$ satisfy $p\restriction M_i$ does not $\mu $ -fork over $M_0$ for all $1\leq i<\delta $ . Then p also does not $\mu $ -fork over $M_0$ .

Proof For $1\leq i<\delta $ , since $p\restriction M_i$ does not $\mu $ -fork over $M_0$ , we can find $M^i<_uM_0$ of size $\mu $ such that $p\restriction M_i$ does not $\mu $ -split over $M^i$ . By monotonicity of nonsplitting, $p\restriction M_i$ does not $\mu $ -split over $M_0$ . By continuity of $\mu $ -nonsplitting, p does not $\mu $ -split over $M_0$ . Since $M^1<_u M_0<_u M_1<_u M_\delta $ , by weak transitivity (Proposition 3.12) p does not $\mu $ -split over $M^1$ . (By a similar argument, it does not $\mu $ -split over other $M^i$ .) By definition p does not $\mu $ -fork over $M_0$ .

We now show uniqueness of nonforking in $K_{\mu }$ , by generalizing the argument in [35]. Instead of superstability, we stick to our Assumption 2.1. Fact 2.9 in that paper will be replaced by our Proposition 4.2. The requirement that $M_0,M_1$ be limit models is removed.

Proposition 4.5 (Uniqueness 1).

Let $M_0\leq M_1$ in $K_{\mu }$ and $p_0\neq p_1\in \operatorname {gS}(M_1)$ both do not $\mu $ -fork over $M_0$ . If in addition $p_{\langle \rangle }:= p_0\restriction M_0=p_1\restriction M_0$ , then $p_0=p_1$ .

Proof Suppose the proposition is false. Let $N_0<_u M_0$ and $N_1<_uM_0$ such that $p_0$ does not $\mu $ -split over $N_0$ while $p_1$ does not $\mu $ -split over $N_1$ (necessarily $N_0\neq N_1$ by weak uniqueness of nonsplitting). We will build a u-increasing and continuous $\langle M_i:i\leq \mu \rangle \subseteq K_{\mu }$ and a coherent $\langle p_\eta \in \operatorname {gS}(M_{l(\eta )}):\eta \in 2^{\leq \mu }\rangle $ such that for all $\nu \in 2^{<\mu }$ , $p_{\nu ^\frown 0}$ and $p_{\nu ^\frown 1}$ are distinct nonforking extensions of $p_{\nu }$ . If done $\{p_\eta :\eta \in 2^\mu \}$ will contradict stability in $\mu $ .

The base case is given by the assumption. For successor case, suppose $M_i$ and $\{p_\eta :\eta \in 2^i\}$ have been constructed for some $1\leq i<\mu $ . Define $M_{i+1}'$ to be a $(\mu ,\omega )$ -limit over $M_i$ . Fix $\eta \in 2^i$ , we will define $p_{\eta ^\frown 0},p_{\eta ^\frown 1}\in \operatorname {gS}(M_{i+1}')$ nonforking extensions of $p_\eta $ (nonsplitting will be witnessed by different models; otherwise weak uniqueness of nonsplitting applies). Since $p_\eta $ does not $\mu $ -fork over $M_0$ , we can find $N_{\eta }<_uM_0$ such that $p_\eta $ does not $\mu $ -split over $N_\eta $ . Pick $p_\eta ^+\in \operatorname {gS}(M_{i+1}')$ a nonsplitting extension of $p_\eta $ . On the other hand, obtain $N_\eta '<_uN^*<_uM_0$ such that $N^*$ is a $(\mu ,\omega )$ -limit over $N_\eta '$ and $N_\eta '>_uN_\eta $ . By uniqueness of limit models over $N_\eta $ of the same length, there is $f:M_{i+1}'\cong _{N_\eta '}N^*$ .

By invariance of nonsplitting, $f(p_\eta ^+)$ does not $\mu $ -split over $N_\eta $ . By monotonicity of nonsplitting, $p_\eta $ , and hence $p_\eta \restriction N^*$ does not $\mu $ -split over $N_\eta $ . $f(p_\eta ^+)\restriction N_\eta '=p_\eta ^+\restriction N_\eta '=(p_\eta \restriction N^*)\restriction N_\eta '$ . By weak uniqueness of $\mu $ -nonsplitting, $f(p_\eta ^+)=p_\eta \restriction N^*$ . Since $p_\eta \restriction N^*$ has two nonforking extensions $p_0\neq p_1\in \operatorname {gS}(M_1)$ where $M_1>_uN^*$ , we can obtain their isomorphic copies $p_{\eta ^\frown 0}\neq p_{\eta ^\frown 1}\in \operatorname {gS}(M_{i+1})$ for some $M_{i+1}>_uM_{i+1}'$ . They still do not $\mu $ -fork over $M_0$ because $M_0$ is fixed (actually $p_{\eta ^\frown i}$ does not $\mu $ -split over $N_i<_uM_0$ ). Ensure coherence at the end.

For limit case, let $\eta \in 2^\delta $ for some limit ordinal $\delta \leq \mu $ . Define $p_\eta \in \operatorname {gS}(M_\delta )$ to be the direct limit of $\langle p_{\eta \restriction i}:i<\delta \rangle $ . By Proposition 4.4, $p_\eta $ does not $\mu $ -fork over $M_0$ .

Corollary 4.6 (Uniqueness 2).

Let $M\leq N$ in $K_{\geq \mu }$ and $p,q\in \operatorname {gS}(N)$ both do not $\mu $ -fork over M. If in addition $p\restriction M=q\restriction M$ , then $p=q$ .

Proof Proposition 4.5 takes care of the case $M,N\in K_{\mu }$ . Suppose the corollary is false, then $p\neq q$ and there exist $N^p,N^q<_uM$ such that p does not $\mu $ -fork over $N^p$ and q does not $\mu $ -fork over $N^q$ . We have two cases:

1. 1. Suppose $M\in K_{\mu }$ but $N\in K_{>\mu }$ . By tameness obtain $N'\in K_{\mu }$ such that $M\leq N'\leq N$ and $p\restriction N'\neq q\restriction N'$ . Together with $p\restriction M=q\restriction M$ , it contradicts Proposition 4.5.

2. 2. Suppose $M\in K_{>\mu }$ . Obtain $M^p,M^q\leq M$ of size $\mu $ that are universal over $N^p$ and $N^q$ , respectively. By Löwenheim–Skolem axiom, pick $M'\leq M$ of size $\mu $ containing $M^p$ and $M^q$ . Thus $M'$ is universal over both $N^p$ and $N^q$ , and $p\restriction M'=q\restriction M'$ . Since $p\neq q$ , tameness gives some $N'\in K_{\mu }$ , $M'\leq N'\leq N$ such that $p\restriction N'\neq q\restriction N'$ , which contradicts Proposition 4.5.

Remark 4.7. The strategy of case (2) cannot be applied to Proposition 4.5 because $M'$ might coincide with M and we do not have enough room to invoke weak uniqueness of nonsplitting. This calls for a specific proof in Proposition 4.5. Similarly, we cannot simply invoke weak uniqueness of nonsplitting to prove case (2) because we do not know if M is also universal over $M'$ .

Corollary 4.8 (Transitivity).

Let $M_0\leq M_1\leq M_2$ be in $K_{\geq \mu }$ , $p\in \operatorname {gS}(M_2)$ . If $\mathbf {K}$ is stable in $[\Vert M_1 \Vert ,\Vert M_2 \Vert ]$ , p does not $\mu $ -fork over $M_1$ and $p\restriction M_1$ does not $\mu $ -fork over $M_0$ , then p does not $\mu $ -fork over $M_0$ .

Proof By Proposition 4.2, obtain $q\supseteq p\restriction M_1$ a nonforking extension in $\operatorname {gS}(M_2)$ . Both q and p do not fork over $M_1$ and $q\restriction M_1=p\restriction M_1$ . By Corollary 4.6, $p=q$ , but q does not $\mu $ -fork over $M_0$ .

For local character, we imitate [33, Lemma 4.11] which handled the case of $\mu ^+$ -saturated models ordered by $\leq _{\mathbf {K}}$ instead of $<_u$ . That proof originates from [24, II Claim 2.11(5)].

Proposition 4.9 (Local character).

Let $\delta \geq \chi $ be regular, $\langle M_i:i\leq \delta \rangle \subseteq K_{\geq \mu }$ u-increasing and continuous, $p\in \operatorname {gS}(M_\delta )$ . There is $i<\delta $ such that p does not $\mu $ -fork over $M_i$ .

Proof If $\delta \geq \mu ^+$ , then by existence of nonsplitting (Proposition 3.12) and monotonicity, there is $j<\delta $ such that p does not $\mu $ -split over $M_j$ . As $M_{j+1}$ is universal over $M_j$ , p does not $\mu $ -fork over $M_{j+1}$ .

If $\chi \leq \delta \leq \mu $ and suppose the conclusion fails, then we can build:

1. 1. $\langle N_i:i\leq \delta \rangle \subseteq K_{\mu }$ u-increasing and continuous.

2. 2. $\langle N_i':i\leq \delta \rangle \subseteq K_{\mu }$ increasing and continuous.

3. 3. $N_0=N_0'\leq M_0$ be any model in $K_{\mu }$ .

4. 4. For all $i<\delta $ , $N_i\leq M_i$ and $N_i\leq N_i'\leq M_\delta $ .

5. 5. For all $i<\delta $ , $\bigcup _{j\leq i}(|N_j'|\cap |M_{i+1}|)\subseteq |N_{i+1}|.$

6. 6. For all $j<\delta $ , $p\restriction N_{j+1}' \ \mu $ -splits over $N_j$ .

We specify the successor step of $N_i'$ : suppose $N_i$ has been constructed. Since $p \mu $ -forks over $M_i$ , hence over $N_i$ . Thus $(N_{i-1},N_i)$ cannot witness nonforking, so there is $N_i'\in K_{\mu }$ with $N_i\leq N_i'\leq M_\delta $ such that $p\restriction N_i' \ \mu $ -splits over $N_{i-1}$ . After the construction, by monotonicity $p\restriction N_\delta \supseteq p\restriction N_i' \ \mu $ -splits over $N_{i-1}$ for each successor i, contradicting $\chi $ -local character of $\mu $ -nonsplitting.

In Section 6, we will need the original form of [33, Lemma 4.11], whose proof is similar to Proposition 4.9. We write the statement here for comparison.

Fact 4.10. Let $\delta \geq \chi $ be regular, $\langle M_i:i\leq \delta \rangle $ be an increasing and continuous chain of $\mu ^+$ -saturated models, $p\in \operatorname {gS}(M_\delta )$ . There is $i<\delta $ such that p does not $\mu $ -fork over $M_i$ .

We now show the promised continuity of nonforking. In [33, Lemma 4.12], the chain must be of length $\geq \chi $ . We do not have the restriction here because we have continuity of nonsplitting in Assumption 2.1.

Proposition 4.11 (Continuity 2).

Let $\delta <\mu ^+$ be regular, $\langle M_i:i\leq \delta \rangle \subseteq K_{\geq \mu }$ u-increasing and continuous, and $\mathbf {K}$ is stable in $[\Vert M_1 \Vert ,\Vert M_\delta \Vert )$ . Let $p\in \operatorname {gS}(M_\delta )$ satisfy $p\restriction M_i$ does not $\mu $ -fork over $M_0$ for all $1\leq i<\delta $ . Then p also does not $\mu $ -fork over $M_0$ .

Proof If $\delta \geq \chi $ , by Proposition 4.9 there is $i<\delta $ such that p does not $\mu $ -fork over $M_i$ . By Corollary 4.8, p does not $\mu $ -fork over $M_0$ .

If $\delta <\chi \leq \mu $ , we have two cases: (1) $M_0\in K_{\mu }$ : then for $1\leq i<\delta $ , $p\restriction M_i$ does not $\mu $ -split over $M_0$ . By Proposition 3.17, p does not $\mu $ -split over $M_0$ , so p does not $\mu $ -fork over $M_1$ . By Corollary 4.8, p does not $\mu $ -fork over $M_0$ . (2) $M_0\in K_{>\mu }$ : for $1\leq i<\delta $ , let $N_i<_u M_0$ witness $p\restriction M_i$ does not $\mu $ -fork over $M_0$ . By Löwenheim–Skolem axiom, there is $N\in K_{\mu }$ (here we need $\delta \leq \mu $ ) such that $N_i<_uN\leq M_0$ for all i. Apply case (1) with N replacing $M_0$ .

Existence is more tricky because nonforking requires the base to be universal over the witness of nonsplitting. The second part of the proof is based on [33, Lemma 4.9].

Proposition 4.12 (Existence).

Let M be a $(\geq \mu ,\geq \chi )$ -limit model, $p\in \operatorname {gS}(M)$ . Then p does not $\mu $ -fork over M. Alternatively M can be a $\mu ^+$ -saturated model.

Proof The first part is immediate from Proposition 4.9. For the second part, apply existence of nonsplitting Proposition 3.12 to obtain $N\in K_{\mu }$ , $N\leq M$ such that p does not $\mu $ -split over N. By model-homogeneity, M is universal over N, hence p does not $\mu $ -fork over M.

Corollary 4.13. There exists a good $\mu $ -frame over the $\mu $ -skeleton of $(\mu ,\geq \chi )$ -limit models ordered by $\leq _u$ , except for symmetry and local character $\chi $ in place of ${\aleph _0}$ .

Proof Define nonforking as in Definition 4.1(2). Invariance and monotonicity are immediate. Existence is by Proposition 4.12, $\chi $ -local character is by Proposition 4.9, extension is by Proposition 4.2, uniqueness is by Proposition 4.5, and continuity is by Proposition 4.4.

Remark 4.14.

1. 1. We do not expect $\aleph _0$ -local character because there are strictly stable AECs. For the same reason we restrict models to be $(\mu ,\geq \chi )$ -limit to guarantee existence property.

2. 2. Let $\lambda \geq \mu $ . Our frame extends to $([\mu ,\lambda ],\geq \chi )$ -limit models if we assume stability in $[\mu ,\lambda ]$ . However [33] has already developed $\mu $ -nonforking for $\mu ^+$ -saturated models ordered by $\leq $ , and we will see in Corollary 6.2(2) that under extra stability assumptions, $(>\mu ,\geq \chi )$ -limit models are automatically $\mu ^+$ -saturated, so the interesting part is $K_{\mu }$ here.

3. 3. We will see in Corollary 5.13(2) that symmetry also holds if we have enough stability.

Since we have built an approximation of a good frame in Corollary 4.13, one might ask if it is canonical. We first observe the following fact (Assumption 2.1 is not needed):

Fact 4.15 [37, Theorem 14.1].

Let $\lambda \geq \operatorname {LS}(\mathbf {K})$ . Suppose $\mathbf {K}$ is $\lambda $ -superstable and there is an independence relation over the limit models (ordered by $\leq $ ) in $K_\lambda $ , satisfying invariance, monotonicity, universal local character, uniqueness, and extension. Let $M\leq N$ be limit models in $K_\lambda $ and $p\in \operatorname {gS}(N)$ . Then p is independent over M iff p does not $\lambda $ -fork over M.

Its proof has the advantage that it does not require the independence relation to be for longer types as in [7, Corollary 5.19]. However, it still uses the following lemma from [7, Lemma 4.2]:

Lemma 4.16. Suppose there is an independence relation over models in $K_{\mu }$ ordered by $\leq $ . If it satisfies invariance, monotonicity, and uniqueness, then the relation is extended by $\mu $ -nonsplitting.

Proof Suppose $M\leq N$ in $K_{\mu }$ , $p\in \operatorname {gS}(N)$ is independent over M. For any $N_1,N_2\in K_{\mu }$ with $M\leq N_1,N_2\leq N$ , and any $f:N_1\cong _MN_2$ . We need to show that $f(p)\restriction N_2=p\restriction N_2$ . By monotonicity, $p\restriction N_1$ and $p\restriction N_2$ do not depend on M. By invariance, $f(p)\restriction N_2$ is independent over M. By uniqueness and the fact that f fixes M, we have $f(p)\restriction N_2=p\restriction N_2$ .

In the above proof, it utilizes the assumption that the independence relation is for models ordered by $\leq $ , so it makes sense to talk about $p\restriction N_i$ is independent over M for $i=1,2$ . To generalize Fact 4.15 to our frame in Corollary 4.13, one way is to assume the independence relation to be for models ordered by $\leq $ , and with universal local character $\chi $ . But since we defined our frame to be for models ordered by $\leq _u$ , we want to keep the weaker assumption that the arbitrary independence relation is also for models ordered by $\leq _u$ . Thus we cannot directly invoke Lemma 4.16, where the $N_i$ ’s are not necessarily universal over M. To circumvent this, we adapt the lemma by allowing more room:

Lemma 4.17. Let $M<_uN<_uN'$ all in $K_{\mu }$ , $p\in \operatorname {gS}(N')$ . If $p\restriction N \ \mu $ -splits over M, then p also $\mu $ -splits over M with witnesses universal over M. Namely, there are $N_1',N_2'\leq N'$ such that $N_1'>_uM$ , $N_2'>_uM$ and there is $f':N_1'\cong _MN_2'$ with $f(p)\restriction N_2'\neq p\restriction N_2'$ .

Proof By assumption, there are $N_1,N_2\in K_{\mu }$ such that $M\leq N_1,N_2\leq N$ and there is $f:N_1\cong _MN_2$ such that $f(p\restriction N)\restriction N_2\neq p\restriction N_2$ . Extend f to an isomorphism $\tilde {f}$ of codomain N, and let $N^*\geq N_1$ be the domain of $\tilde {f}$ . Since $N>_uM$ , by invariance $N^*>_uM$ . On the other hand, $N'>_uN$ , then $N'>_uN_1$ and there is $g:N^*\xrightarrow [N_1]{}N'$ . Let the image of g be $N^{**}.$

In the diagram below, we use dashed arrows to indicate isomorphisms. Solid arrows indicate $\leq $ .

Since $\tilde {f}\circ g^{-1}:N^{**}\cong _{M}N$ and $M<_u N^{**},N\leq N'$ , we consider $\tilde {f}\circ g^{-1}(p)\restriction N$ and $p\restriction N$ .

$$ \begin{align*} \tilde{f}\circ g^{-1}(p)\restriction N&\geq[\tilde{f}\circ g^{-1}(p)]\restriction N_2\\ &=\tilde{f}([g^{-1}(p)]\restriction N_1)\restriction N_2\quad\text{as } \tilde{f}^{-1}[N_2]=N_1\\ &=\tilde{f}(p\restriction N_1)\restriction N_2\quad\text{as } g \text{ fixes } N_1\\ &=f(p\restriction N_1)\restriction N_2\quad\text{as } \tilde{f} \text{ extends } f\\ &=f(p\restriction N)\restriction N_2\quad\text{as } f^{-1}[N_2]=N_1\leq N\\ p\restriction N&\geq p\restriction N_2. \end{align*} $$

Since $f(p\restriction N)\restriction N_2\neq p\restriction N_2$ , $\tilde {f}\circ g^{-1}(p)\restriction N\neq p\restriction N$ and we can take $N_1':= N^{**}$ , $N_2':= N$ , $f':=\tilde {f}\circ g^{-1}$ in the statement of the lemma.

Now we can prove a canonicity result for our frame. In order to apply Lemma 4.17, we will need to enlarge N to a universal extension in order to have more room. This procedure is absent in the original forward direction of Fact 4.15 but is similar to the backward direction (to get q below).

Proposition 4.18. Suppose there is an independence relation over the $(\mu ,\geq \chi )$ -limit models ordered by $\leq _u$ satisfying invariance, monotonicity, local character $\chi $ , uniqueness, and extension. Let $M<_u N$ be $(\mu ,\geq \chi )$ -limit models and $p\in \operatorname {gS}(N)$ . Then p is independent over M iff p does not $\mu $ -fork over M.

Proof Suppose p is independent over M. By assumption M is a $(\mu ,\delta )$ -limit for some regular $\delta \in [\chi ,\mu ^+)$ . Resolve $M=\bigcup _{i<\delta }M_i$ such that all $M_i$ are also $(\mu ,\delta )$ -limit. By local character, $p\restriction M$ is independent over $M_i$ for some $i<\delta $ . Since the independence relation satisfies uniqueness and extension, by the proof of Corollary 4.8 it also satisfies transitivity. Therefore p is independent over $M_i$ . Let $N'>_uN$ . By extension, there is $p'\in \operatorname {gS}(N')$ independent over $M_i$ and $p'\supseteq p$ . Now suppose $p \ \mu $ -splits over $M_i$ , by Lemma 4.17 $p' \ \mu $ -splits over $M_i$ with universal witnesses, contradicting Lemma 4.16 (where $\leq $ is replaced by $<_u$ where). As a result, p does not $\mu $ -split over $M_i$ . Since $M_i<_u M$ , p does not $\mu $ -fork over M.

Conversely suppose p does not $\mu $ -fork over M. By local character and monotonicity, $p\restriction M$ is independent over M. By extension, obtain $q\in \operatorname {gS}(N)$ independent over M and $q\supseteq p$ . From the forward direction, q does not $\mu $ -fork over M. By Proposition 4.5, $p=q$ so invariance gives q independent over M.

To conclude this section, we show that the existence of a frame similar to Corollary 4.13 is sufficient to obtain local character of nonsplitting. Continuity of $\mu $ -nonsplitting and $\mu $ -tameness in Assumption 2.1 are not needed.

Proposition 4.19. Let $\delta <\mu ^+$ be regular. Suppose there is an independence relation over the $(\mu ,\geq \delta )$ -limit models ordered by $\leq _u$ satisfying invariance, monotonicity, local character $\delta $ , uniqueness, and extension. Then $\mathbf {K}$ has $\delta $ -local character of $\mu $ -nonsplitting.

Proof Let $\langle M_i:i\leq \delta \rangle $ be u-increasing and continuous, $p\in \operatorname {gS}(M_\delta )$ . There is $i<\delta $ such that p is independent over $M_i$ . By the forward direction of Proposition 4.18 (local character of nonsplitting is not used), p does not $\mu $ -split over $M_i$ .

5 Local symmetry

Tower analysis was used in [29, Theorem 3] to connect a notion of $\mu $ -symmetry and reduced towers. Combining with [17], superstability and $\mu $ -symmetry imply the uniqueness of limit models. VanDieren and Vasey [31, Lemma 4.6] observed that a weaker form of $\mu $ -symmetry is sufficient to deduce one direction of [29, Theorem 3], and enough superstability implies the weaker form of $\mu $ -symmetry. Therefore enough superstability already implies the uniqueness of limit models [31, Corollary 1.4]. Meanwhile, [10] localized the notion of $\mu $ -symmetry and deduced the uniqueness of limit models of length $\geq \chi $ . We will imitate the above argument and replace the hypothesis of local symmetry by sufficient stability. As a corollary we will obtain symmetry property of nonforking. The uniqueness of limit models will be discussed in the next section.

The following is based on [10, Definition 10]. They restricted $M_0$ to be exactly $(\mu ,\delta )$ -limit over N but they should mean $(\mu ,\geq \delta )$ for the proofs to go through. We will use $\delta :=\chi $ in this paper.

Definition 5.1. Let $\delta <\mu ^+$ be a limit ordinal. $\mathbf {K}$ has $(\mu ,\delta )$ -symmetry for $\mu $ -nonsplitting if for any $M,M_0,N\in K_{\mu }$ , elements $a,b$ with:

1. 1. $a\in M-M_0$ ;

2. 2. $M_0<_uM$ and $M_0$ is $(\mu ,\geq \delta )$ -limit over N;

3. 3. $\operatorname {gtp}(a/M_0)$ does not $\mu $ -split over N;

4. 4. $\operatorname {gtp}(b/M)$ does not $\mu $ -split over $M_0$ ,

then there is $M^b\in K_{\mu }$ universal over $M_0$ and containing b such that $\operatorname {gtp}(a/M^b)$ does not $\mu $ -split over N. We will abbreviate $(\mu ,\delta )$ -symmetry for $\mu $ -nonsplitting as $(\mu ,\delta )$ -symmetry.

Now we localize the hierarchy of symmetry properties in [31, Definition 4.3]. The first two items will be important in our improvement of [10].

Definition 5.2. Let $\delta <\mu ^+$ be a limit ordinal. In the following items, we always let $a\in M-M_0$ , $M_0<_uM$ , $M_0$ be $(\mu ,\geq \delta )$ -limit over N and b be an element. In the conclusion, $M^b\in K_{\mu }$ universal over $M_0$ and containing b is guaranteed to exist.

1. 1. $\mathbf {K}$ has uniform $(\mu ,\delta )$ -symmetry: If $\operatorname {gtp}(b/M)$ does not $\mu $ -split over $M_0$ , $\operatorname {gtp}(a/M_0)$ does not $\mu $ -fork over $(N,M_0)$ , then $\operatorname {gtp}(a/M^b)$ does not $\mu $ -fork over $(N,M_0)$ .

2. 2. $\mathbf {K}$ has weak uniform $(\mu ,\delta )$ -symmetry: If $\operatorname {gtp}(b/M)$ does not $\mu $ -fork over $M_0$ , $\operatorname {gtp}(a/M_0)$ does not $\mu $ -fork over $(N,M_0)$ , then $\operatorname {gtp}(a/M^b)$ does not $\mu $ -fork over $(N,M_0)$ .

3. 3. $\mathbf {K}$ has nonuniform $(\mu ,\delta )$ -symmetry: If $\operatorname {gtp}(b/M)$ does not $\mu $ -split over $M_0$ , $\operatorname {gtp}(a/M_0)$ does not $\mu $ -fork over $M_0$ , then $\operatorname {gtp}(a/M^b)$ does not $\mu $ -fork over $M_0$ .

4. 4. $\mathbf {K}$ has weak nonuniform $(\mu ,\delta )$ -symmetry: If $\operatorname {gtp}(b/M)$ does not $\mu $ -fork over $M_0$ , $\operatorname {gtp}(a/M_0)$ does not $\mu $ -fork over $M_0$ , then $\operatorname {gtp}(a/M^b)$ does not $\mu $ -fork over $M_0$ .

The following results generalize [31, Section 4] which assumes superstability and works with full symmetry properties.

Proposition 5.3. Let $\delta <\mu ^+$ be a limit ordinal. $(\mu ,\delta )$ -symmetry is equivalent to uniform $(\mu ,\delta )$ -symmetry. Both imply nonuniform $(\mu ,\delta )$ -symmetry and weak uniform $(\mu ,\delta )$ -symmetry. Nonuniform $(\mu ,\delta )$ -symmetry implies weak nonuniform $(\mu ,\delta )$ -symmetry.

Proof In the definition of the symmetry properties, we always have $N<_uM_0$ , so the following are equivalent:

• • $\operatorname {gtp}(a/M_0)$ does not $\mu $ -fork over $(N,M_0)$ ;

• • $\operatorname {gtp}(a/M_0)$ does not $\mu $ -split over N.

Similarly, the following are equivalent:

• • $\operatorname {gtp}(a/M^b)$ does not $\mu $ -fork over $(N,M_0)$ ;

• • $\operatorname {gtp}(a/M^b)$ does not $\mu $ -split over N.

Therefore, $(\mu ,\delta )$ -symmetry is equivalent to uniform $(\mu ,\delta )$ -symmetry.

Uniform $(\mu ,\delta )$ -symmetry implies weak uniform $(\mu ,\delta )$ -symmetry because nonforking over $M_0$ is a stronger assumption than nonsplitting over $M_0$ . Uniform $(\mu ,\delta )$ -symmetry implies nonuniform $(\mu ,\delta )$ -symmetry because the latter does not require the witness to nonforking be the same, so its conclusion is weaker. Nonuniform $(\mu ,\delta )$ -symmetry implies weak nonuniform $(\mu ,\delta )$ -symmetry because nonforking over $M_0$ is a stronger assumption than nonsplitting over $M_0$ .

The following result modifies the proof of [10] which involves a lot of tower analysis. We will only mention the modifications and refer the readers to the original proof.

Proposition 5.4. Let $\delta <\mu ^+$ be a limit ordinal. If $\delta \geq \chi $ , then weak uniform $(\mu ,\delta )$ -symmetry implies uniform $(\mu ,\delta )$ -symmetry.

Proof sketch

[10, Theorem 18 and Proposition 19] establish that $(\mu ,\delta )$ -symmetry is equivalent to continuity of reduced towers at $\geq \delta $ . We will show that the backward direction only requires weak uniform $(\mu ,\delta )$ -symmetry. Then using the equivalence twice we deduce that weak uniform $(\mu ,\delta )$ -symmetry implies $(\mu ,\delta )$ -symmetry. By the previous proposition, it is equivalent to uniform $(\mu ,\delta )$ -symmetry.

There are three places in [10, Theorem 18] which use $(\mu ,\delta )$ -symmetry. In the first two paragraphs of page 11:

1. 1. By $\chi $ -local character, there is a successor $i^*<\delta $ such that $\operatorname {gtp}(b/M_\delta ^\delta )$ does not $\mu $ -split over $M_{i^*}^{i^*}$ .

2. 2. For any $j<\delta $ , $M_\delta ^\delta $ is universal over $M_{j}^{j}$ .

3. 3. For any $j<\delta $ , $\operatorname {gtp}(a_{j}/M_{j}^{j})$ does not $\mu $ -split over $N_{j}$ .

4. 4. For any successor $j<\delta $ , $M_j^j$ is $(\mu ,\geq \delta )$ -limit over $M_{j-1}^{j-1}$ and over $N_j$ .

Let $j^*:= i^*+1$ which is still a successor ordinal less than $\delta $ . Combining (1) and (4), we have $\operatorname {gtp}(b/M_\delta ^\delta )$ does not $\mu $ -fork over $M_{j^*}^{j^*}$ . Combining (3) and (4), $\operatorname {gtp}(a_{j^*}/M_{j^*}^{j^*})$ does not $\mu $ -fork over $M_{j^*}^{j^*})$ . Moreover, (2) gives $M_\delta ^\delta $ is universal over $M_{j^*}^{j^*}$ . Together with (4) and weak uniform $(\mu ,\delta )$ -symmetry, we can find $M^b \ (\mu ,\geq \delta )$ -limit over $M_{j^*}^{j^*}$ and containing b such that $\operatorname {gtp}(a/M^b)$ does not $\mu $ -fork over $(N_{j^*},M_{j^*}^{j^*})$ . In other words, $\operatorname {gtp}(a/M^b)$ does not $\mu $ -split over $N_{j^*}$ and so the original argument goes through with $i^*$ replaced by $j^*$ .

In “Case 2” on page 12:

1. a. $\operatorname {gtp}(b/\bigcup _{l<\alpha }M_l^l)$ does not $\mu $ -split over $M_{i^*}^{i^*}$ .

2. b. $i^*+2\leq k<\alpha $ and $\operatorname {gtp}(a_k/M_k^{k+1})$ does not $\mu $ -split over $N_k$ .

3. c. $M_k^{k+1}$ is universal over $M_{i^*}^{i^*}$ .

4. d. $\bigcup _{l<\alpha }M_l^l$ is universal over $M_k^{k+1}$ . $M_k^{k+1}$ is $(\mu ,\geq \delta )$ -limit over $N_k$ .

Combining (a) and (c), $\operatorname {gtp}(b/\bigcup _{l<\alpha }M_l^l)$ does not $\mu $ -fork over $M_k^{k+1}$ . (b) gives $\operatorname {gtp}(a_k/M_k^{k+1})$ does not $\mu $ -fork over $(N_k,M_k^{k+1})$ . Together with (d) and weak uniform $(\mu ,\delta )$ -symmetry, we can find $M^b_k \ (\mu ,\geq \delta )$ -limit over $M_{k}^{k+1}$ and containing b such that $\operatorname {gtp}(a_k/M^b_k)$ does not $\mu $ -fork over $(N_{k},M_{k}^{k+1})$ so the proof goes through (we do not change index this time).

Before “Case 1” on page 11, they refer the successor case to the original proof of [29, Theorem 3] which also uses $(\mu ,\delta )$ -symmetry. But the idea from the previous case applies equally.

In [35, Corollary 2.18], it was shown that under superstability, weak nonuniform $\mu $ -symmetry implies weak uniform $\mu $ -symmetry. We generalize this as the following.

Proposition 5.5. Let $\delta <\mu ^+$ be a limit ordinal. Weak nonuniform $(\mu ,\delta )$ -symmetry implies weak uniform $(\mu ,\delta )$ -symmetry.

Proof Using the notation in Definition 5.2, we assume $\operatorname {gtp}(b/M)$ does not $\mu $ -fork over $M_0$ and $\operatorname {gtp}(a/M_0)$ does not $\mu $ -fork over $(N,M_0)$ . By weak nonuniform $(\mu ,\delta )$ -symmetry, we can find $M^b$ such that $\operatorname {gtp}(a/M^b)$ does not $\mu $ -fork over $M_0$ . Since $\operatorname {gtp}(a/M_0)$ does not $\mu $ -fork over $(N,M_0)$ , by extension of nonsplitting (Proposition 3.12), there is $a'$ such that $\operatorname {gtp}(a/M_0)=\operatorname {gtp}(a'/M_0)$ and $\operatorname {gtp}(a'/M^b)$ does not $\mu $ -split over N. Now both $\operatorname {gtp}(a/M^b)$ and $\operatorname {gtp}(a'/M^b)$ do not $\mu $ -fork over $M_0$ and they agree on the restriction of $M_0$ . By uniqueness of nonforking (Proposition 4.5), $\operatorname {gtp}(a/M^b)=\operatorname {gtp}(a'/M^b)$ and hence $\operatorname {gtp}(a/M^b)$ does not $\mu $ -split over N. In other words, it does not $\mu $ -fork over $(N,M_0)$ as desired.

Corollary 5.6. The following are equivalent:

1. 0. $(\mu ,\chi )$ -symmetry for $\mu $ -nonsplitting.

2. 1. Uniform $(\mu ,\chi )$ -symmetry.

3. 2. Weak uniform $(\mu ,\chi )$ -symmetry.

4. 3. Nonuniform $(\mu ,\chi )$ -symmetry.

5. 4. Weak nonuniform $(\mu ,\chi )$ -symmetry.

Proof By Proposition 5.3, (0) and (1) are equivalent, (1) implies (2) and (3) while (3) implies (4). By Proposition 5.4 (this is where we need $\chi $ instead of a general $\delta $ ), (2) implies (1). By Proposition 5.5, (4) implies (2).

The following adapts [31, Lemma 5.6] and fills in some gaps. In particular we need $\mu $ -tameness (in Assumption 2.1) and stability in $\Vert N_\alpha \Vert $ for the proof to go through. It is not clear how to remove $\mu $ -tameness which they do not assume.

Lemma 5.7. Let $M_0\in K_{\mu }$ , $N_\alpha \in K_{\geq \mu }$ with $M_0\leq N_\alpha $ , $b,b_\beta \in |N_\alpha |$ , $a_\alpha $ be an element. If $\mathbf {K}$ is stable in $\Vert N_\alpha \Vert $ , $\operatorname {gtp}(a_\alpha /N_\alpha )$ does not $\mu $ -fork over $M_0$ and $\operatorname {gtp}(b/M_0)=\operatorname {gtp}(b_\beta /M_0)$ , then $\operatorname {gtp}(a_\alpha b/M_0)=\operatorname {gtp}(a_\alpha b_\beta /M_0)$ .

Proof Let $M^*<_u M_0$ witness that $\operatorname {gtp}(a_\alpha /N_\alpha )$ does not $\mu $ -fork over $(M^*,M_0)$ . By stability, extend $N_\alpha $ to $N^*>_u N_\alpha $ such that $\operatorname {gtp}(a_\alpha /N^*)$ does not $\mu $ -split over $M^*$ . As $\operatorname {gtp}(b/M_0)=\operatorname {gtp}(b_\beta /M_0)$ , there is $f:N_\alpha \xrightarrow [M_0]{N^*}$ such that $f(b)=b_\beta $ . As $\operatorname {gtp}(a_\alpha /N_\alpha )$ does not $\mu $ -split over $M^*$ , by Proposition 3.4 $\operatorname {gtp}(f(a_\alpha )/f(N_\alpha ))=\operatorname {gtp}(a_\alpha /f(N_\alpha ))$ . Hence there is $g\in \operatorname {Aut}_{f(N_\alpha )}\mathfrak {C}$ such that $g(f(a_\alpha ))=a_\alpha $ . Then

$$ \begin{align*}\operatorname{gtp}(a_\alpha b/M_0)=\operatorname{gtp}(f(a_\alpha)f(b)/M_0)=\operatorname{gtp}(g(f(a_\alpha))f(b)/M_0)=\operatorname{gtp}(a_\alpha b_\beta/M_0).\end{align*} $$

Remark 5.8. By swapping the dummy variables, we have the following formulation: Let $M_0\in K_{\mu }$ , $N_\beta '\in K_{\geq \mu }$ with $M_0\leq N_\beta '$ , $a,a_\alpha \in |N_\beta '|$ , $b_\beta $ be an element. If $\mathbf {K}$ is stable in $\Vert N_\beta ' \Vert $ , $\operatorname {gtp}(b_\beta /N_\beta ')$ does not $\mu $ -fork over $M_0$ and $\operatorname {gtp}(a/M_0)=\operatorname {gtp}(a_\alpha /M_0)$ , then $\operatorname {gtp}(ab_\beta /M_0)=\operatorname {gtp}(a_\alpha b_\beta /M_0)$ .

The following adapts [31, Lemma 5.7] which assumes superstability in $[\mu ,\lambda )$ . When we write the $\mu $ -order property, we mean tuples that witness order property have length $\mu $ .

Proposition 5.9. Let $\lambda \geq \mu $ be a cardinal. If $\mathbf {K}$ is stable in $[\mu ,\lambda )$ and fails $(\mu ,\chi )$ -symmetry, then it has the $\mu $ -order property of length $\lambda $ .

Proof By Corollary 5.6(2) $\Rightarrow $ (0), $\mathbf {K}$ fails weak uniform $(\mu ,\chi )$ -symmetry. So there are $N,M_0,M\in K_{\mu }$ and elements $a,b$ such that:

• • $a\in M-M_0$ , $M_0<_uM$ and $M_0$ is $(\mu ,\geq \chi )$ -limit over N.

• • $\operatorname {gtp}(b/M)$ does not $\mu $ -fork over $M_0$ .

• • $\operatorname {gtp}(a/M_0)$ does not $\mu $ -fork over $(N,M_0)$ .

• • There is no $M^b\in K_{\mu }$ universal over $M_0$ containing b such that $\operatorname {gtp}(a/M^b)$ does not $\mu $ -fork over $(N,M_0)$ .

Build $\langle a_\alpha ,b_\alpha ,N_\alpha ,N_\alpha '\rangle $ increasing and continuous such that for $\alpha <\lambda $ :

1. 1. $N_\alpha ,N_\alpha '\in K_{\mu +|\alpha |}$ ;

2. 2. $b\in |N_0|$ and $N_0$ is universal over M;

3. 3. $N_\alpha <_u N_\alpha '<_uN_{\alpha +1}$ ;

4. 4. $a_\alpha \in |N_\alpha '|$ and $\operatorname {gtp}(a_\alpha /M_0)=\operatorname {gtp}(a/M_0)$ ;

5. 5. $b_\alpha \in |N_{\alpha +1}|$ and $\operatorname {gtp}(b_\alpha /M)=\operatorname {gtp}(b/M)$ ;

6. 6. $\operatorname {gtp}(a_\alpha /N_\alpha )$ does not $\mu $ -fork over $(N,M_0)$ ;

7. 7. $\operatorname {gtp}(b_\alpha /N_\alpha ')$ does not $\mu $ -fork over $M_0$ .

$N_0$ is specified in (2). We specify the successor step: suppose $N_\alpha $ has been constructed, by Corollary 4.3 there is $a_\alpha $ such that $\operatorname {gtp}(a_\alpha /N_\alpha )$ extends $\operatorname {gtp}(a/M_0)$ and does not $\mu $ -fork over $(N,M_0)$ . Build any $N_\alpha '$ universal over $N_\alpha $ containing $a_\alpha $ . By Proposition 4.2 again, there is $b_\alpha $ such that $\operatorname {gtp}(b_\alpha /N_\alpha ')$ extends $\operatorname {gtp}(b/M)$ and does not $\mu $ -fork over $M_0$ . Build $N_{\alpha +1}$ universal over $N_\alpha '$ containing $b_\alpha $ . Notice that stability is used to guarantee the existence of $N_\alpha ,N_\alpha '$ and the extension of types.

After the construction, we have the following properties for $\alpha ,\beta <\lambda $ :

1. a. $\operatorname {gtp}(a_\alpha b/M_0)\neq \operatorname {gtp}(ab/M_0)$ ;

2. b. $\operatorname {gtp}(ab_\beta /M_0)=\operatorname {gtp}(ab/M_0)$ ;

3. c. If $\beta <\alpha $ , $\operatorname {gtp}(ab/M_0)\neq \operatorname {gtp}(a_\alpha b_\beta /M_0)$ ;

4. d. If $\beta \geq \alpha $ , $\operatorname {gtp}(ab/M_0)=\operatorname {gtp}(a_\alpha b_\beta /M_0)$ .

Suppose (a) is false. By invariance and the choice of $a,b,M_0,N$ there is no $M'\in K_{\mu }$ universal over $M_0$ containing b such that $\operatorname {gtp}(a_\alpha /M')$ does not $\mu $ -fork over $(N,M_0)$ . This contradicts $M':= N_\alpha $ and item (6) in the construction. (b) is true because of item (5) of the construction and $a\in |M|$ . For (c), items (5), (6) and Lemma 5.7 (with the exact same notations) imply $\operatorname {gtp}(a_\alpha b_\beta /M_0)=\operatorname {gtp}(a_\alpha b/M_0)$ which is not equal to $\operatorname {gtp}(ab/M_0)$ by (a). For (d), items (4), (7) and Remark 5.8 imply $\operatorname {gtp}(a_\alpha b_\beta /M_0)=\operatorname {gtp}(ab_\beta /M_0)$ which is equal to $\operatorname {gtp}(ab/M_0)$ by (b).

To finish the proof, let d enumerate $M_0$ , and for $\alpha <\lambda $ , $c_\alpha := a_\alpha b_\alpha d$ . By (c) and (d) above, $\langle c_\alpha :\alpha <\lambda \rangle $ witnesses the $\mu $ -order property of length $\lambda $ .

Remark 5.10. When proving (d), we used Remark 5.8 which requires $\operatorname {gtp}(b_\beta /N_\beta ')$ nonforking over $M_0$ , and this is from extending $\operatorname {gtp}(b/M)$ nonforking over $M_0$ . This called for the failure of weak uniform $(\mu ,\chi )$ -symmetry instead of just $(\mu ,\chi )$ -symmetry. (In the original proof, they claimed the same for (c) in place of (d), which should be a typo.)

Question 5.11. Is it possible to weaken the stability assumption in Proposition 5.9?

Fact 5.12. For any infinite cardinal $\lambda $ , $h(\lambda ):=\beth _{(2^{\lambda })^+}$ . When we write the $\mu $ -stable, we mean stability of tuples of length $\mu $ .

1. 1. [23, Claim 4.6] If $\mathbf {K}$ does not have the $\mu $ -order property, then there is $\lambda <h(\mu )$ such that $\mathbf {K}$ does not have the $\mu $ -order property of length $\lambda $ .

2. 2. [7, Fact 5.13] If $\mathbf {K}$ is $\mu $ -stable (in some cardinal $\geq \mu $ ), then it does not have the $\mu $ -order property.

3. 3. If $\mathbf {K}$ is stable in some $\lambda =\lambda ^\mu $ , then $\mathbf {K}$ is $\mu $ -stable in $\lambda $ .

4. 4. [16, Corollary 6.4] If $\mathbf {K}$ is stable and tame in $\mu $ (these are in Assumption 2.1), then it is stable in all $\lambda =\lambda ^\mu $ . In particular it is stable in $2^\mu $ .

5. 5. For some $\lambda <h(\mu )$ , $\mathbf {K}$ does not have the $\mu $ -order property of length $\lambda $ .

Proof For (1) and (2), see also [20, Proposition 3.4] for a proof sketch. (3) is an immediate corollary of [5, Theorem 3.1], see [20, Theorem 2.1] for a proof. We show (5): by (4) $\mathbf {K}$ is stable in $2^\mu $ . By (3) it is $\mu $ -stable in $2^\mu $ . Combining with (2) and (1) gives the conclusion.

Corollary 5.13. There is $\lambda <h(\mu )$ such that if $\mathbf {K}$ is stable in $[\mu ,\lambda )$ , then:

1. 1. $\mathbf {K}$ has $(\mu ,\chi )$ -symmetry;

2. 2. the frame in Corollary 4.13 satisfies symmetry.

Proof

1. 1. By Fact 5.12(5), there is $\lambda <h(\mu )$ such that $\mathbf {K}$ does not have the $\mu $ -order property of length $\lambda $ . By the contrapositive of Proposition 5.9, $\mathbf {K}$ has $(\mu ,\chi )$ -symmetry.

2. 2. By (1) and Proposition 5.3, $\mathbf {K}$ has weak nonuniform $(\mu ,\chi )$ -symmetry. Compared to symmetry in a good frame, weak nonuniform $(\mu ,\chi )$ -symmetry has the extra assumption that $\operatorname {gtp}(a/M_0)$ does not $\mu $ -fork over $M_0$ , but this is always true by Proposition 4.12.

6 Symmetry and saturated models

As mentioned in the previous section, [31, Corollary 1.4] deduced symmetry from superstability and obtained the uniqueness of limit models. It is natural to localize such argument, which was partially done in the following.

Fact 6.1 [10, Theorem 20].

Assume $\mathbf {K}$ has $(\mu ,\chi )$ -symmetry (together with Assumption 2.1). Then it has the uniqueness of $(\mu ,\geq \chi )$ -limit models: let $M_0,M_1,M_2\in K_{\mu }$ . If both $M_1$ and $M_2$ are $(\mu ,\geq \chi )$ -limit over $M_0$ , then $M_1\cong _{M_0}M_2$ .

In the original proof of the above fact, they did not assume tameness. However, we will need tameness when we remove the symmetry assumption (see also the discussion before Lemma 5.7).

Corollary 6.2. There is $\lambda <h(\mu )$ such that if $\mathbf {K}$ is stable in $[\mu ,\lambda )$ , then:

1. 1. $\mathbf {K}$ has the uniqueness of $(\mu ,\geq \chi )$ -limit models.

2. 2. If also $\mu>\operatorname {LS}(\mathbf {K})$ , any $(\mu ,\geq \chi )$ -limit model is saturated.

Proof

1. 1. By Corollary 5.13(1), $\mathbf {K}$ has $(\mu ,\chi )$ -symmetry. Apply Fact 6.1.

2. 2. Suppose $\mu $ is regular. Since $\chi \leq \mu $ , any $(\mu ,\geq \chi )$ -limit is isomorphic to a $(\mu ,\mu )$ -limit, which is saturated. Suppose $\mu $ is singular. Let M be a $(\mu ,\geq \chi )$ -limit model. We show that it is $\delta $ -saturated for any regular $\delta <\mu $ . Since $\delta +\chi $ is a regular cardinal in $[\chi ,\mu ^+)$ , M is also $(\mu , \delta +\chi )$ -limit, which implies it is $(\delta +\chi )$ -saturated.

Before stating a remark, we quote a fact in order to compare Vasey’s results with ours (but we will not use that fact in our paper). Continuity of $\mu $ -nonsplitting in Assumption 2.1 is not needed.

Fact 6.3 [11, Theorem 5.15].

Let $\chi _0\geq 2^\mu $ be such that $\mathbf {K}$ does not have the $\mu $ -order property of length $\chi _0^+$ , define $\chi _1:=(2^{2^{\chi _0}})^{+3}$ , and let $\xi \geq \chi _1$ . If $\mathbf {K}$ is stable in unboundedly many cardinals $<\xi $ , then any increasing chain of $\xi $ -saturated models of length $\geq \chi $ is $\xi $ -saturated.

Remark 6.4. We assumed enough stability to get a local result: the same $\mu $ was considered throughout. In contrast, [38, Theorems 6.3 and 11.7] are eventual: Fact 6.3 was heavily used. Some of the hypotheses there require unboundedly many ( $H_1$ -closed) stability cardinals.

Now we turn to an AEC version of Harnik’s Theorem. [38, Lemma 11.9] improved [30, Theorem 1] and showed that the following.

Fact 6.5. Let $\mathbf {K}$ be $\mu $ -tame with a monster model. Let $\xi \geq \mu ^+$ . Suppose:

1. 1. $\mathbf {K}$ is stable in $\mu $ and $\xi $ ;

2. 2. $\langle M_i:i<\delta \rangle $ is an increasing chain of $\xi $ -saturated models;

3. 3. $\operatorname {cf}(\delta )\geq \chi $ ;

4. 4. $(\xi ,\delta )$ -limit models are saturated,

then $\bigcup _{i<\delta }M_i$ is $\xi $ -saturated.

We remove the assumption of (4) by assuming more stability and continuity of nonsplitting. Our proof is based on [38, Lemma 11.9] which have some omissions. For comparison, we write down all the assumptions.

Proposition 6.6. Let $\mathbf {K}$ be $\mu $ -tame with a monster model. Let $\xi \geq \mu ^+$ . There is $\lambda <h(\xi )$ such that if:

1. 1. $\mathbf {K}$ is stable in $\mu $ and $[\xi ,\lambda )$ ,

2. 2. $\langle M_i:i<\delta \rangle $ is an increasing chain of $\xi $ -saturated models;

3. 3. $\operatorname {cf}(\delta )\geq \chi $ ;

4. 4. continuity of $\mu $ -nonsplitting and of $\xi $ -nonsplitting holds,

then $\bigcup _{i<\delta }M_i$ is $\xi $ -saturated.

Before proving the proposition, we need to justify that the local character $\chi $ (Definition 3.10), which was defined for $K_{\mu }$ , also applies to $K_\xi $ . In other words, we need to show that $K_\xi $ has local character of nonsplitting (at most) $\chi $ . (Vasey usually cited this fact as [33, Section 4], by which he should mean an adaptation of [33, Lemma 4.11].)

Lemma 6.7 (Local character transfer).

If $\mathbf {K}$ is stable in some $\xi \geq \mu $ , then it has $\chi $ -local character of $\xi $ -nonsplitting.

Proof Let $\langle M_i:i\leq \delta \rangle $ be u-increasing and continuous in $K_\xi $ , $p\in \operatorname {gS}(M_\delta )$ . By Proposition 4.9, there is $i<\delta $ such that p does not $\mu $ -fork over $M_{i}$ . By definition of nonforking, there is $N<_uM_i$ of size $\mu $ such that p does not $\mu $ -split over N. Suppose $p \ \xi $ -splits over $M_{i}$ then it also $\xi $ -splits over N. By $\mu $ -tameness, it $\mu $ -splits over N, contradiction.

Proof of Proposition 6.6

Let $\delta \geq \chi $ be regular. If $\delta \geq \xi $ we can use a cofinality argument. So we assume $\delta <\xi $ . Let $M_\delta :=\bigcup _{i<\delta }M_i$ and $N\in K_\xi $ , $N\leq M_\delta $ . Without loss of generality, we may assume for $i\leq \delta $ , $M_i\in K_\xi $ : Given a saturated $M^*\in K_{\geq \xi ^+}$ and some $N\leq M^*$ of size $\leq \xi $ , we can close N into a $(\xi ,\chi )$ -limit $N^*$ . By $\xi $ -model-homogeneity of $M^*$ , we may assume $N^*\leq M^*$ . By Lemma 6.7 and Corollary 6.2(2), any $(\xi ,\geq \chi )$ -limits are saturated, so $N^*$ is saturated. Therefore we can recursively shrink each $M_i$ to a saturated model in $K_\xi $ while still containing the same intersection with N.

Extend p to a type in $\operatorname {gS}(M_\delta )$ . By Fact 4.10, there is $i<\delta $ such that p does not $\mu $ -fork over $M_i$ . By reindexing assume $i=0$ and let $M_0^0\in K_{\mu }$ witness the nonforking. Obtain $N_0\in K_{\mu }$ such that $M_0^0<_uN_0\leq M_0$ in $K_{\mu }$ . Define $\mu ':=\mu +\delta $ , we build $\langle N_i:1\leq i\leq \delta \rangle $ increasing and continuous in $K_{\mu '}$ such that $N_0\leq N_1\leq N\leq N_\delta $ and for $i\leq \delta $ , $N_i\leq M_i$ . Now we construct:

1. 1. $\langle M_i^*,f_{i,j}:i\leq j<\delta \rangle $ an increasing and continuous directed system.

2. 2. For $i<\delta $ , $M_i^*\in K_\xi $ , $N_i\leq M_i^*\leq M_i$ .

3. 3. For $i<\delta $ , $f_{i,i+1}:M_i^*\xrightarrow [N_i]{}M_{i+1}^*$ .

4. 4. $M_0^*:= M_0$ . For $i<\delta $ , $M_i^*<_uM_{i+1}^*$ .

At limit stage $i<\delta $ , take direct limit $M_i^*$ which contains $N_i$ . Since $\Vert N_i \Vert <\xi $ and $M_i$ is model-homogeneous, we may assume $M_i^*$ is inside $M_i$ . Suppose $M_i^*$ is constructed for some $i<\delta $ , obtain the amalgam $M_{i+1}^{**}$ of $M_i^*$ and $N_{i+1}$ over $N_i$ . Since $\Vert N_{i+1} \Vert <\xi $ and $M_{i+1}$ is model-homogeneous, we may embed the amalgam into $M_{i+1}$ . Call the image of the amalgam $M_{i+1}^*$ . After the construction, take one more direct limit to obtain $(M_\delta ^*,f_{i,\delta })_{i<\delta }$ (but this time we do not know if $M_\delta ^*\leq M_\delta $ ). By item (4) above, we have that $M_\delta ^*$ is a $(\xi ,\delta )$ -limit, hence saturated.

We will work in a local monster model, namely we find a saturated $\tilde {M}\in K_\xi $ such that:

1. a. $\tilde {M}$ contains $M_\delta $ and $M_\delta ^*$ .

2. b. For $i<\delta $ , $f_{i,\delta }$ can be extended to $f_{i,\delta }^*\in \operatorname {Aut}(\tilde {M})$ .

3. c. For $i<\delta $ , $f_{i,\delta }^*[N_\delta ]\leq M_\delta ^*$ .

(c) is possible because $M_\delta ^*$ is universal over $f_{i,\delta }[M_i^*]$ . Finally, we define $N^*\leq M_\delta ^*$ of size $\mu '$ containing $\bigcup _{i<\delta }f_{i,\delta }^*[N_\delta ]$ . By model-homogeneity of $M_\delta ^*$ , we build $M^{**}\in K_\xi $ saturated such that $N^*\leq M^{**}<_uM_\delta ^*$ .

By Proposition 4.2, extend p to $q\in \operatorname {gS}(\tilde {M})$ nonforking over $N_0$ (here we need $N_0\in K_{\mu }$ or else we have to assume more stability). Since $M_\delta ^*>_uM^{**}$ , we can find $b_\delta \in M_\delta ^*$ such that $b_\delta \vDash q\restriction M^{**}$ . Since $M_\delta ^*$ is a direct limit of the $M_i^*$ ’s, there is $i<\delta $ such that $f_{i,\delta }(b)=b_\delta $ . As $b\in M_i^*\subseteq M_i\leq M_\delta $ , it suffices to show that $b\vDash q\restriction (f_{i,\delta }^*)^{-1}[M^{**}]$ , because $N\leq N_\delta \leq (f_{i,\delta }^*)^{-1}[N^*]\leq (f_{i,\delta }^*)^{-1}[M^{**}]$ . In the following diagram, dotted arrows refer to $\leq $ or $<_u$ between models, while the dashed equal sign is our goal.

Since $q\restriction M^{**}=\operatorname {gtp}(b_\delta /M^{**})$ does not $\mu $ -fork over $N_0$ and $f_{i,\delta }^*$ fixes $N_i\geq N_0$ , by invariance $\operatorname {gtp}(b/(f_{i,\delta }^*)^{-1}[M^{**}])$ does not $\mu $ -fork $N_0$ . By monotonicity, q and hence $q\restriction (f_{i,\delta }^*)^{-1}[M^{**}]$ does not $\mu $ -fork over $N_0$ . By invariance again, $\operatorname {gtp}(b/N_0)=\operatorname {gtp}(b_\delta /N_0)=q\restriction N_0$ . By Corollary 4.6, $q\restriction (f_{i,\delta }^*)^{-1}[M^{**}]=\operatorname {gtp}(b/(f_{i,\delta }^*)^{-1}[M^{**}])$ as desired.

Remark 6.8.

1. 1. In Proposition 6.6, the assumption of stability in $[\xi ,\lambda )$ is to guarantee local symmetry from no $\xi $ -order property of length $\lambda $ . We can relax the stability assumption if we have the stronger assumption of no $\xi $ -order property. Namely, if $\mathbf {K}$ does not have $\xi $ -order property of length $\zeta $ where $\zeta>\xi $ , then we can simply assume stability in $[\xi ,\zeta )$ .

2. 2. We compare our approach with Vasey’s. To satisfy hypothesis (4) in Fact 6.5, he used Fact 6.1 which requires $(\xi ,\chi )$ -symmetry and continuity of nonsplitting [38, Theorem 11.11(1)]. Meanwhile he obtained the equivalence of $(\xi ,\chi )$ -symmetry $\Leftrightarrow $ the increasing union of saturated models of length $\geq \chi $ in $K_{\xi ^+}$ is saturated (see Fact 6.15). By Fact 6.3, the latter is true for large enough $\xi $ . In short, he raised the cardinal threshold while we assumed more stability. More curiously, both our stability assumption and his cardinal threshold are linked to no order property.

   A comparison table can be found below. For $\xi \geq \mu $ , we abbreviate the increasing union of saturated models of length $\geq \chi $ in $K_{\xi }$ is saturated by “Union( $\xi $ ).”

Observation 6.9. The $[\xi ,\lambda )$ stability assumption in Proposition 6.6 can be replaced by $(\xi ,\chi )$ -symmetry, because we can directly apply Fact 6.1 instead of using extra stability to invoke Corollary 6.2. This applies to other results in the paper.

We now recover two known results with different proofs. The original proof for [32, Proposition 10.10] is extremely abstract so we supplement a direct argument. (Here we already assumed a monster model which implies no maximal models everywhere. Alternatively, one can adapt the proof of [4, Theorem 7.1] without using symmetry to transfer no maximal models upward.) On the other hand, since we have generalized the arguments in [31], we can specialize them to $\chi ={\aleph _0}$ and recover [31, Corollary 6.10] (see below). In their approach, [30, Theorem 22] was cited for the successor case of $\lambda $ and the limit case was proven by inductive hypothesis. Here we show each case of $\lambda $ separately in Corollary 6.11(2). They also glossed over the computation of the Löwenheim–Skolem number so we add details.

The following facts do not require continuity of nonsplitting.

Fact 6.10.

1. 1. [1, Theorem 1] Let $\xi \geq \mu $ . If $\mathbf {K}$ is stable in $\xi $ , then it is also stable in $\xi ^{+n}$ for all $n<\omega $ .

2. 2. [33, Theorem 5.5] Let $\xi \geq \mu $ , $\delta $ be regular, $\langle \xi _i:i<\delta \rangle $ be strictly increasing stability cardinals and $\xi _0=\xi $ . If $\mathbf {K}$ has $\delta $ -local character of $\xi $ -nonsplitting, then $\sup _{i<\delta }\xi _i$ is also a stability cardinal. In particular, if $\mathbf {K}$ is $\xi $ -superstable, then it is stable in all $\lambda \geq \xi $ .

Corollary 6.11.

1. 1. [32, Proposition 10.10] Let $\xi \geq \mu $ . If $\mathbf {K}$ is $\xi $ -superstable, then it is superstable in all $\zeta \geq \xi $ .

2. 2. Let $\xi \geq \mu ^+$ . If $\mathbf {K}$ is $\xi $ -superstable, then $\mathbf {K}^{\boldsymbol {\xi \text {-}sat}}$ the class of $\xi $ -saturated models in $\mathbf {K}$ forms an AEC with Löwenheim–Skolem number $\xi $ .

3. 3. [31, Corollary 6.10] Let $\xi \geq \mu ^+$ . If $\mathbf {K}$ is $\xi $ -superstable, then for $\lambda \geq \xi $ , $\mathbf {K}^{\boldsymbol {\lambda \text {-}sat}}$ the class of $\lambda $ -saturated models in $\mathbf {K}$ forms an AEC with Löwenheim–Skolem number $\lambda $ .

Proof

1. 1. Combine Fact 6.10(2) and Lemma 6.7.

2. 2. By (1) and Proposition 3.16, we have continuity of $\xi $ -nonsplitting and stability in $[\xi ,\infty )$ . By Proposition 6.6, $\mathbf {K}^{\boldsymbol {\xi \text {-}sat}}$ is closed under chains. Given a $\xi $ -saturated model M and $A\subseteq |M|$ , we need to find $N\leq M$ containing A such that $\Vert N \Vert \leq |A|+\xi $ . We prove this by induction on $|A|$ . The first paragraph of the proof of Proposition 6.6 shows how to handle the case $|{A}|\leq \xi $ . Suppose $|{A}|>\xi $ , then resolve $A=\bigcup _{i<|A|}{A_i}$ where $A_i$ are increasing and of size $<|A|$ . For each $i<|A|$ , use the inductive hypothesis and close each $A_i$ into a $\xi $ -saturated $N_i\leq M$ of size $|A_i|+\xi $ with $N_i\geq N_j$ for $j<i$ . As $\mathbf {K}^{\boldsymbol {\xi \text {-}sat}}$ is closed under chains, $\bigcup _{i<|A|}N_i$ is $\xi $ -saturated, of size $|A|$ and contains A.

3. 3. Combine (1) and (2).

It is natural to ask if there are converses to our results. In particular what are the sufficient conditions to $\mathbf {K}$ having the $\chi $ -local character in $K_\xi $ for some $\xi \geq \mu $ . Vasey [38, Lemma 4.12] gave one useful criterion which we adapt below. The original statement did not cover the case $\delta =\xi $ below and such omission affects the rest of his results. In particular [38, Theorem 4.11] should only apply to singular $\mu $ there. Our result covers regular cardinals because we assume stability and continuity of nonsplitting. Only in [38, Section 11] did he start to assume continuity of nonsplitting and in [38, Theorem 12.1] did he take care of the regular case by under extra assumptions.

We state the full assumptions in the following proposition.

Proposition 6.12. Let $\mu \geq \operatorname {LS}(\mathbf {K})$ . Suppose $\mathbf {K}$ has a monster model, is $\mu $ -tame and stable in some $\xi \geq \mu ^+$ . Let $\delta <\xi ^+$ be regular, $\langle M_i:i\leq \delta \rangle $ be u-increasing and continuous in $K_\xi $ , $M_\delta $ is $(\mu +\delta )^+$ -saturated and $p\in \operatorname {gS}(M_\delta )$ . There is $i<\delta $ such that p does not $\xi $ -split over $M_i$ if one of the following holds:

1. 1. $\delta =\xi $ (so $\xi $ is regular), $\mathbf {K}$ has continuity of $\xi $ -nonsplitting.

2. 2. $\delta =\xi $ , $\mathbf {K}$ is stable in $\mu $ and has continuity of $\mu $ -nonsplitting.

3. 3. $\delta <\xi $ .

Proof The first case is by Proposition 3.9 (with $\xi $ in place of $\mu $ ). The second case is by Lemma 6.7. We consider the case $\delta <\xi $ . Suppose the conclusion is false, then for $i<\delta $ , there exist:

1. 1. $N_i^0,N_i^1,N_i^2\in K_\xi $ with $N_i^0\leq N_i^1,N_i^2\leq M_\delta $ .

2. 2. $f_i:N_i^1\xrightarrow [N_i^0]{}N_i^2$ with $f_i(p\restriction N_i^1)\neq p\restriction N_i^2$ .

3. 3. $M_i^1\leq N_i^1$ and $M_i^2\leq N_i^2$ such that $f_i[M_i^1]\cong M_i^2$ and $f_i(p\restriction M_i^1)\neq p\restriction M_i^2$ .

Let $N\leq M$ of size $\mu +\delta $ containing $M_i^1$ and $M_i^2$ for all $i<\delta $ . Since $M_\delta $ is $(\mu +\delta )^+$ -saturated, there is $b\in |M_\delta |$ realizing $p\restriction N$ . Then there is $i<\delta $ such that $b\in |M_i|$ . Since $f_i$ fixes $M_i$ , it also fixes b. Thus

$$ \begin{align*} f_i(p\restriction M_i^1)=\operatorname{gtp}(f(b)/M_i^2)=\operatorname{gtp}(b/M_i^2)=p\restriction M_i^2, \end{align*} $$

contradicting item (3) above.

Corollary 6.13. Suppose $\xi \geq \mu ^+$ and $\delta <\xi ^+$ be regular. If $\mathbf {K}$ is stable in $\xi $ , has continuity of $\xi $ -nonsplitting and has unique $(\xi ,\geq \delta )$ -limit models, then it has $\delta $ -local character in $K_\xi $ . If in addition $K_\xi $ has unique limit models, then it is $\xi $ -superstable.

Proof Let $\delta '\geq \delta $ be regular and $\langle M_i:i\leq \delta '\rangle $ be u-increasing and continuous, $p\in \operatorname {gS}(M_{\delta '})$ . By the proof of Corollary 6.2(2), $M_{\delta '}$ is saturated. By Proposition 6.12, there is $i<\delta '$ such that p does not $\xi $ -split over $M_i$ .

Remark 6.14. As before, our result is local. Grossberg and Vasey [18, Theorem 3.18] proved a similar result which is eventual: they managed to guarantee superstability after $\beth _\omega (\chi _0)$ where $\mathbf {K}$ has no order property of length $\chi _0$ .

Vasey [38, Fact 11.6] also made another observation that connects saturated models and symmetry. In the original statement, he omitted writing continuity of nonsplitting in the hypothesis and did not give a proof sketch, so we give more details here (Assumption 2.1 applies). As in the discussion before Definition 5.1, we consider the tail of regular cardinals $\delta '\geq \delta $ in place of a fixed $\delta '=\delta $ to match our notations.

Fact 6.15. Let $\delta <\mu ^+$ be regular. If for any $\delta '\in [\delta ,\mu ^+)$ regular, any $\langle M_i:i<\delta '\rangle $ increasing chain of saturated models in $K_{\mu ^+}$ has a saturated union, then $ \mathbf {K}$ has $(\mu ,\delta )$ -symmetry.

Proof In [29, Theorem 2], it was shown that if the above fact holds for any $\delta <\mu ^+$ , then any reduced tower is continuous at all $\delta <\mu ^+$ . We can localize this argument to show that if the above fact holds for a specific $\delta <\mu ^+$ , then any reduced tower is continuous at $\geq \delta $ . By [10, Proposition 19], $\mathbf {K}$ has $(\mu ,\delta )$ -symmetry.

Corollary 6.16. Let $\delta <\mu ^+$ be regular. If for any $\delta '\in [\delta ,\mu ^+)$ regular, any $\langle M_i:i<\delta '\rangle $ increasing chain of saturated models in $K_{\mu ^+}$ has a saturated union, then $ \mathbf {K}$ has uniqueness of $(\mu ,\geq \delta )$ -limit models.

Proof Combine Fact 6.15 and Fact 6.1.

Question 6.17. Is there an analog of Fact 6.15 and Corollary 6.16 where “ $\mu ^+$ ” is replaced by a general $\xi \geq \mu ^+$ ?

We look at superlimits and solvability before ending this section. The following localizes [25, Definition 2.1], which is more natural than [38, Definition 6.2].

Definition 6.18. Let $\xi \geq \mu $ . $M\in K_\xi $ is a $\chi $ -superlimit if M is universal in $K_\xi $ , not maximal, and for any regular $\delta $ with $\chi \leq \delta <\xi ^+$ , $\langle M_i:i<\delta \rangle $ increasing such that $M_i\cong M$ for all $i<\delta $ , then $\bigcup _{i<\delta }M_i\cong M$ . M is called a superlimit if it is a ${\aleph _0}$ -superlimit.

Proposition 6.19. Let $\mathbf {K}$ have continuity of $\xi $ -nonsplitting for some $\xi \geq \mu ^+$ . There is $\lambda <h(\xi )$ such that if $\mathbf {K}$ is stable in $[\xi ,\lambda )$ , then it has a saturated $\chi $ -superlimit in $K_\xi $ .

Proof By Corollary 6.2(2) and Lemma 6.7, any $(\xi ,\geq \chi )$ -limit M is saturated (hence universal in $K_\xi $ ). Let $\delta $ be regular, $\chi \leq \delta <\xi ^+$ , $\langle M_i:i<\delta \rangle $ increasing such that $M_i\cong M$ for all $i<\delta $ . Then all $M_i$ are saturated in $K_\xi $ . By Proposition 6.6, $\bigcup _{i<\delta }M_i$ is also saturated, hence isomorphic to M.

Remark 6.20. The specific $\chi $ -superlimit built above is saturated. Under the same assumptions, it is true for all $\chi $ -superlimits (Lemma 6.23).

The following connects superlimit models with solvability (see [18, Definition 2.17] for a definition).

Fact 6.21 [18, Lemma 2.19].

Let $\lambda \geq \xi $ . The following are equivalent:

1. 1. $\mathbf {K}$ is $(\lambda ,\xi )$ -solvable.

2. 2. There exists an AEC $\mathbf {K'}$ in ${\operatorname {L}(\mathbf {K'})}\supseteq \operatorname {L}( \mathbf {K})$ such that $\operatorname {LS}(\mathbf {K'})\leq \xi $ , $\mathbf {K'}$ has arbitrarily large models and for any $M\in K^{\prime }_\lambda $ , $M\restriction \operatorname {L}(\mathbf {K})$ is a superlimit in $\mathbf {K}$ .

In [18, Theorem 4.9], they showed that $(\lambda ,\xi )$ -solvability is eventually (in $\lambda $ ) equivalent to other criteria of superstability (modulo a jump of $\beth _{\omega +2}$ ). Also, $\lambda $ is required to be greater than $\xi $ . We propose that a better formulation of superstability which has $\lambda =\xi $ . The case $\lambda>\xi $ should be a stronger condition because it allows downward transfer (see [36, Corollary 5.1] for more development on this). Our result proceeds with a series of lemmas.

The next lemma generalizes [18, Fact 2.8(5)] (which is based on [13]).

Lemma 6.22. Let $\xi \geq \mu ^+$ and let M be a saturated model in $K_\xi $ . M is a $\chi $ -superlimit iff for any regular $\delta $ with $\chi \leq \delta <\xi ^+$ , any increasing chain of saturated models in $K_\xi $ of length $\delta $ has a saturated union.

Proof Immediate from the definition of a $\chi $ -superlimit. Notice that we need $\delta <\xi ^+$ to make sure that the chain of saturated models have a union in $K_\xi $ .

The following lemma generalizes [13, Theorem 2.3.11].

Lemma 6.23. Let $\xi>\operatorname {LS}(\mathbf {K})$ . If M is a $\chi $ -superlimit in $K_\xi $ , then M is saturated.

Proof We show that M is a $(\xi ,\delta )$ -limit for regular $\delta \in [\chi ,\xi ^+)$ . If done, the argument in Corollary 6.2(2) shows that it is saturated. Construct $\langle M_i,N_i:i<\delta \rangle $ in $K_\xi $ such that $M_0:= M\cong M_i<_uN_i<M_{i+1}$ for $i<\delta $ . Suppose $N_i$ is constructed, by universality $N_i$ embeds inside M so we can build $M_{i+1}$ , an isomorphic copy of M over $N_i$ . To construct $M_i$ for limit i, we embed the union of previous $N_i$ inside M and repeat the above process. By the property of a $\chi $ -superlimit, $M\cong \bigcup _{i<\delta }M_i=\bigcup _{i<\delta }N_i$ which is a $(\xi ,\delta )$ -limit.

Proposition 6.24.

1. 1. Let $\xi \geq \mu ^+$ , $\mathbf {K}$ have continuity of $\xi $ -nonsplitting and be stable in $\xi $ . $\mathbf {K}$ is $\xi $ -superstable iff it is $(\xi ,\xi )$ -solvable.

2. 2. If $\mu>\operatorname {LS}(\mathbf {K})$ and $\mathbf {K}$ is $(<\mu )$ -tame, then it is $\mu $ -superstable iff it is $(\mu ^+,\mu ^+)$ -solvable.

Proof

1. 1. Suppose $\mathbf {K}$ is $\xi $ -superstable. By Lemma 6.23, superlimits in $K_\xi $ are saturated. By Corollary 6.11(2), $\xi $ -saturated models are closed under chains. By Lemma 6.22, saturated models in $K_\xi $ are superlimits. Therefore, saturated models and superlimits coincide in $K_\xi $ . By Fact 6.21, we can define $\operatorname {L}(\mathbf {K'}):=\operatorname {L}(\mathbf {K})$ and $ \mathbf {K'}$ to be the class of $\xi $ -saturated models. By Corollary 6.11(2) again, it is an AEC with $\operatorname {LS}(\mathbf {K'})=\xi $ .

   The backward direction only requires $\xi>\operatorname {LS}(\mathbf {K})$ instead of $\xi \geq \mu ^+$ : suppose $\mathbf {K}$ is $(\xi ,\xi )$ -solvable. By the proof of Lemma 6.23, superlimits in $K_\xi $ are saturated and are $(\xi ,\delta )$ -limits for $\delta <\xi ^+$ . Now given $\delta <\xi ^+$ , a u-increasing and continuous chain $\langle M_i:i\leq \delta \rangle \subseteq K_\xi $ and $p\in \operatorname {gS}(M_\delta )$ , we need to show that p does not $\xi $ -split over $M_i$ for some $i<\delta $ . As $M_\delta $ is a $(\xi ,\delta )$ -limit, it is also a superlimit and hence saturated. The conclusion follows from Proposition 6.12.

2. 2. The forward direction combines item (1) and Corollary 6.11(1) ( $(<\mu )$ -tameness is not needed). Suppose $\mathbf {K}$ is $(\mu ^+,\mu ^+)$ -solvable. By Lemma 6.23 there is a saturated superlimit in $K_{\mu ^+}$ , which witnesses the union of saturated models in $K_{\mu ^+}$ is $\mu ^+$ -saturated. By Corollary 6.16, it has uniqueness of limit models in $K_{\mu }$ . By $(<\mu )$ -tameness and the proof of Corollary 6.13 (replace “ $\xi $ ” there by $\mu $ and “ $\mu ^+$ ” there by ${\operatorname {LS}( \mathbf {K})}^+$ ), it is $\mu $ -superstable.

Remark 6.25. One might want to generalize the argument to strictly stable AECs. In that case the statement of Fact 6.21(2) should naturally be for a $\chi $ -AEC instead of an AEC, but we do not know how to prove that saturated models are closed under $\chi $ -directed systems (a similar obstacle is in [8, Remark 2.3(4)]). On top of that, the equivalence in Fact 6.21 is not clear in that case because we do not have a first-order presentation theorem on $\chi $ -AECs to extract an Ehrenfeucht–Mostowski blueprint (but we do have a $(<\mu )$ -ary presentation theorem, see [8, Theorem 3.2] or [19, Theorem 5.6]).

7 Stability in a tail and U-rank

In this section we look at two characterizations of superstability. For convenience we follow [38, Section 4] to define some cardinals:

Definition 7.1.

1. 1. $\lambda (\mathbf {K})$ stands for the first stability cardinal above $\operatorname {LS}(\mathbf {K})$ .

2. 2. $\chi (\mathbf {K})$ stands for the least regular cardinal $\delta $ such that $\mathbf {K}$ has $\delta $ -local character of $\xi $ -nonsplitting for some stability cardinal $\xi \geq \operatorname {LS}( \mathbf {K})$ .

3. 3. $\lambda '(\mathbf {K})$ stands for the minimum stability cardinal $\xi $ such that for any stability cardinal $\xi '\geq \xi $ , $\mathbf {K}$ has $\chi (\mathbf {K})$ -local character of $\xi '$ -nonsplitting.

Observation 7.2.

1. 1. By Assumption 2.1, $\lambda (\mathbf {K})\leq \mu $ .

2. 2. By Definition 3.10 (see also the remark after it), $\chi (\mathbf {K})\leq \chi $ .

3. 3. By Lemma 6.7, we can equivalently define $\lambda '(\mathbf {K})$ as the minimum stability cardinal $\xi $ such that $\mathbf {K}$ has $\chi (\mathbf {K})$ -local character of $\xi $ -nonsplitting.

4. 4. $\mathbf {K}$ is eventually superstable ( $\xi $ -superstable for large enough $\xi $ ) iff $\chi ( \mathbf {K})={\aleph _0}$ .

Currently we do not have a nice bound of $\lambda '(\mathbf {K})$ so the cardinal threshold might be very high if we invoke $\lambda '(\mathbf {K})$ or $\chi (\mathbf {K})$ . Vasey built upon [23] and spent several sections to derive:

Fact 7.3 [38, Theorem 11.3(2)].

Suppose $\mathbf {K}$ has continuity of $\xi $ -nonsplitting for all stability cardinal $\xi $ , then $\lambda '( \mathbf {K})<h(\lambda (\mathbf {K}))$ .

We can now state Vasey’s characterization that superstability is equivalent to stability in a tail of cardinals. Since continuity of $\mu $ -nonsplitting is not assumed there, item (1) only holds for singular $\xi $ . Also, the original formulation wrote $\lambda '(\mathbf {K})$ instead of $(\lambda '(\mathbf {K}))^+$ but the proof did not go through.

Fact 7.4. Let $\mathbf {K}$ be $\operatorname {LS}(\mathbf {K})$ -tame with a monster model.

1. 1. [38, Corollary 4.14] Let $\chi _1$ as in Fact 6.3, $\xi \geq (\lambda '(\mathbf {K}))^++\chi _1$ be singular, $\mathbf {K}$ be stable in unboundedly many cardinal $<\xi $ . $\mathbf {K}$ is stable in $\xi $ iff $\operatorname {cf}(\xi )\geq \chi (\mathbf {K})$ .

2. 2. [38, Corollary 4.24] $\chi (\mathbf {K})={\aleph _0}$ iff $\mathbf {K}$ is stable in a tail of cardinals.

We prove a simpler and local analog to Fact 7.4. Rather than looking at the whole tail of cardinals (more accurately the class of singular cardinals with all possible cofinalities) after a potentially high threshold, we directly look for the next $\omega +1$ many cardinals of $\mu $ and verify that $\mathbf {K}$ has enough stability, continuity of nonsplitting and symmetry in those cardinals. Symmetry will be guaranteed by more stability.

Proposition 7.5. There is $\lambda <h(\mu ^{+\omega })$ such that if $\mathbf {K}$ is stable in $[\mu ,\lambda )$ and has continuity of $\mu ^{+\omega }$ -nonsplitting, then it is $\mu ^{+\omega }$ -superstable.

Proof The forward direction does not depend on $\lambda $ and is by Corollary 6.11(1) and Proposition 3.16(1). For the backward direction, obtain $\lambda $ from Corollary 6.2(2) and suppose $\mathbf {K}$ is stable in $[\mu ,\lambda )$ and has continuity of $\mu ^{+\omega }$ . The conclusion of Corollary 6.2(2) (which uses stability in $\mu ^{+\omega }$ and continuity of $\mu ^{+\omega }$ -nonsplitting) gives a saturated model M of size $\mu ^{+\omega }$ . We show that is a $(\mu ^{+\omega },\omega )$ -limit: by stability in $[\mu ,\mu ^{+\omega })$ , build $\langle M_n:n\leq \omega \rangle \subseteq K_{<\mu ^{+\omega }}$ u-increasing and continuous such that for $n<\omega $ , $M_n\in K_{\mu ^{+n}}$ and $M_\omega =M$ . On the other hand, by stability in $\mu ^{+\omega }$ , build $\langle N_i:i\leq \omega \rangle \subseteq K_{\mu ^{+\omega }}$ u-increasing and continuous such that $M_0\leq N_0$ . By a back-and-forth argument, $M\cong _{M_0}N_\omega $ and the latter is a $(\mu ^{+\omega },\omega )$ -limit. By uniqueness of limit models of the same cofinality, any $(\mu ^{+\omega },\omega )$ -limit is saturated.

By Proposition 6.12(3) where $\xi =\mu ^{+\omega }$ , $\delta ={\aleph _0}$ , $\mathbf {K}$ has ${\aleph _0}$ -local character of $\mu ^{+\omega }$ -nonsplitting. Together with stability in $\mu ^{+\omega }$ , we know that $\mathbf {K}$ is superstable in $\mu ^{+\omega }$ .

We state a more general form of the above proposition:

Corollary 7.6. Let $\delta $ be a regular cardinal. There is $\lambda <h(\mu ^{+\delta })$ such that if $\mathbf {K}$ is stable in $[\mu ,\lambda )$ and has continuity of $\mu ^{+\delta }$ -nonsplitting, then it has $\delta $ -local character of $\mu ^{+\delta }$ -nonsplitting. Stability in $[\mu ,\lambda )$ can be replaced by stability in $[\mu ^{+\delta },\lambda )$ and unboundedly many cardinals below $\mu ^{+\delta }$ .

Proof Replace “ $\omega $ ” by $\delta $ in Proposition 7.5. Notice that unboundedly stability many cardinals below $\mu ^{+\delta }$ are sufficient to build $\langle M_i:i<\delta \rangle \subseteq K_{<\mu ^{+\delta }}$ u-increasing.

Remark 7.7.

1. 1. A missing case of Proposition 7.5 is perhaps the regular cardinal ${\aleph _0}$ . In [1, Theorem 2], it was shown that if $\mathbf {K}$ has $\omega $ -locality, $\aleph _0$ -tameness and stability in ${\aleph _0}$ , then $\mathbf {K}$ is stable everywhere. The original proof used a tree argument of height $\omega $ . We provide an alternative proof using our general tools: by $\omega $ -locality and Proposition 3.16(2), $\mathbf {K}$ has continuity of ${\aleph _0}$ -nonsplitting. By Proposition 3.9, $\mathbf {K}$ has ${\aleph _0}$ -local character of ${\aleph _0}$ -nonsplitting. By Corollary 6.11(1), it is (super)stable everywhere.

2. 2. Our proof strategy of Proposition 7.5 is similar to that of [38, Theorem 4.11] but we use different tools. Both assume stability in $\mu ^{+\omega }$ and unboundedly many cardinals in $\mu ^{+\omega }$ . To obtain a saturated model, Vasey raised the threshold of $\mu $ so that the union of $\mu ^{+n}$ -saturated models is $\mu ^{+n}$ -saturated (see Fact 6.3). Then he used an unjustified claim [38, Theorem 4.13] that models in $K_{\mu ^{+\omega }}$ can be closed to a $\mu ^{+n}$ -saturated model (it seems they would invoke [11, Theorem 4.30] but we cannot verify this). These two give a saturated model in $K_{\mu ^{+\omega }}$ . In contrast, we bypass such gap by using the uniqueness of long enough limit models in $K_{\mu ^{+\omega }}$ , this immediately gives us a saturated model in $K_{\mu ^{+\omega }}$ . After that, Vasey and our approaches converge: the saturated model is a $(\mu ^{+\omega },\omega )$ -limit and Proposition 6.12 gives ${\aleph _0}$ -local character of $\mu ^{+\omega }$ -nonsplitting.

Question 7.8.

1. 1. Perhaps under extra assumptions, is it possible to obtain a tighter bound of $\lambda '(\mathbf {K})$ in terms of $\lambda (\mathbf {K})$ than in Fact 7.3?

2. 2. Let $\xi _1,\xi _2$ be stability cardinals. Is there any relationship between continuity of $\xi _1$ -nonsplitting and continuity of $\xi _2$ -nonsplitting? Similarly, can one say anything about continuity of $\xi _1$ -nonsplitting if for unboundedly many stability cardinal $\xi <\xi _1$ , $\mathbf {K}$ has continuity of $\xi $ -nonsplitting? A positive answer might help improve Proposition 7.5.

In [6, Section 7], Boney and Grossberg developed a U-rank for an independence relation over types of arbitrary length.

Definition 7.9. [6, Definition 7.2] Let $\mathbf {K}$ have a monster model and an independence relation over types of length one. U is a class function that maps each Galois type (of length one) in the monster model to an ordinal or $\infty $ , such that for any $M\in K$ , $p\in \operatorname {gS}(M)$ :

1. 1. $U(p)\geq 0$ .

2. 2. For limit ordinal $\alpha $ , $U(p)\geq \alpha $ iff $U(p)\geq \beta $ for all $\beta <\alpha $ .

3. 3. For an ordinal $\beta $ , $U(p)\geq \beta +1$ iff there is $M'\geq M$ , $\Vert M' \Vert =\Vert M \Vert $ and $p'\in \operatorname {gS}(M')$ such that $p'$ is a nonforking (in the sense of the given independence relation) extension of p and $U(p')\geq \beta $ .

4. 4. For an ordinal $\alpha $ , $U(p)=\alpha $ iff $U(p)\geq \alpha $ but $U(p)\not \geq \alpha +1$ .

5. 5. $U(p)=\infty $ iff $U(p)\geq \alpha $ for all ordinals $\alpha $ .

Through a series of lemmas, they managed to obtain the following fact (Assumption 2.1 is not needed).

Fact 7.10 [6, Theorem 7.9].

Let $\mathbf {K}$ have a monster model and an independence relation over types of length one. Suppose the independence relation satisfies invariance and monotonicity. Let $M\in K$ and $p\in \operatorname {gS}(M)$ . The following are equivalent:

1. 1. $U(p)=\infty $ .

2. 2. There is $\langle p_n:n<\omega \rangle $ such that $p_0=p$ and for $n<\omega $ , the domain of $p_n$ has size $\Vert M \Vert $ , and $p_{n+1}$ is a forking extension of $p_n$ .

The original proof proceeds with a lemma followed by the theorem statement. Since the proof of the lemma omitted some details, and that the lemma and the theorem made reference to each other, we straighten the proof as follows:

Lemma 7.11. (2) $\Rightarrow $ (1) holds in Fact 7.10.

Proof By induction on each ordinal $\alpha $ , we show that for each $\alpha $ , for each $n<\omega $ , $U(p_n)\geq \alpha $ . The base case $\alpha =0$ is by the definition of U. The limit case follows from the inductive hypothesis. Suppose we have proven the case $\alpha $ , then for each $n<\omega $ , inductive hypothesis gives $U(p_{n+1})\geq \alpha $ . By the definition of U, $U(p_n)\geq \alpha +1$ .

Lemma 7.12. Let $\mathbf {K}$ have a monster model and an independence relation over types of length one. Suppose the independence relation satisfies invariance and monotonicity. Let $\lambda \geq \operatorname {LS}(\mathbf {K})$ . There is an ordinal $\alpha _\lambda <(2^\lambda )^+$ such that for $M\in K_\lambda $ , $p\in \operatorname {gS}(M)$ , if $U(p)\geq \alpha _\lambda $ then $U(p)=\infty $ .

Proof By invariance, there are at most $2^\lambda $ many U-ranks of types over models of size $\lambda $ . It suffices to show that there is no gap in the U-rank: if $\beta $ is an ordinal, $N\in K_\lambda $ , $q\in \operatorname {gS}(N)$ with $\beta <U(q)<\infty $ , then there is a forking extension $q'$ of q (with domain of size $\lambda $ ) such that $U(q')=\beta $ . Otherwise pick a counterexample $q\in \operatorname {gS}(N)$ . Since $U(q)\geq \beta +1$ , there is a forking extension $q_1$ of q such that $U(q_1)\geq \beta $ . As $U(q_1)$ cannot be $\beta $ , $U(q_1)\geq \beta +1$ . Using monotonicity of forking, we can inductively build $\langle q_n:n<\omega \rangle $ with $q_0:= q$ and for $n<\omega $ , $q_{n+1}$ is a forking extension of $q_n$ . By Lemma 7.11, $U(q_0)=U(q)=\infty $ , contradicting the assumption on $U(q)$ .

Lemma 7.13. Let $\mathbf {K}$ have a monster model and an independence relation over types of length one. Suppose the independence relation satisfies invariance and monotonicity. Then (1) $\Rightarrow $ (2) in Fact 7.10 holds.

Proof Let $\alpha _\lambda $ as in Lemma 7.12 and $p_0:= p$ . Define $\langle p_n:n<\omega \rangle $ inductively such that $U(p_n)=\infty $ . The base case is by assumption on p. Suppose $p_n$ is constructed with $U(p_n)=\infty $ , then in particular $U(p_n)\geq \alpha _\lambda +1$ . By definition of U, there is a forking extension $p_{n+1}$ of $p_n$ (with domain of size $\lambda $ ) such that $U(p_{n+1})\geq \alpha _\lambda $ . By Lemma 7.12 again, $U(p_{n+1})=\infty $ .

Proof of Fact 7.10

Combine Lemma 7.11 and Lemma 7.13.

We have now arrived at an alternative characterization of superstability. At the end of [18, Section 6], they suggested the use of coheir and show that superstability implies bounded U-rank. Since we cannot verify the claim, we use instead $\mu $ -nonforking as the independence relation to characterize superstability as bounded U-rank for limit models in $K_{\mu }$ .

Corollary 7.14. Under Assumption 2.1, restrict $\mu $ -nonforking to limit models in $K_{\mu }$ ordered by $\leq _u$ . Then $ \mathbf {K}$ is $\mu $ -superstable iff $U(p)<\infty $ for all $p\in \operatorname {gS}(M)$ and limit model $M\in K_{\mu }$ .

Proof By Fact 7.10, we need to show $\mu $ -superstability is equivalent to the negation of criterion (2) there. By continuity of $\mu $ -nonforking Proposition 4.4 and the proof of Lemma 3.7, it suffices to prove that $\mu $ -superstability is equivalent to $\mu $ -nonforking having local character ${\aleph _0}$ (under $AP$ it is always possible to extend an omega-chain of types). The forward direction is given by Proposition 4.9 and the backward direction is given by Proposition 4.2, Proposition 4.5, and Proposition 4.19.

We look at one more result of U-rank, which shows the equivalence of being a nonforking extension and having the same U-rank (Fact 7.16). The extra assumption of $\operatorname {LS}(\mathbf {K})$ -witness property for singletons is pointed out by [15, Lemma 8.8] to allow the proof of monotonicity of U-rank [6, Lemma 7.3] to go through. We will adapt their definition of $\operatorname {LS}(\mathbf {K})$ -witness property for singletons because our nonforking is originally defined for model-domains while their independence relations assume set-domains (another approach is perhaps to work in the closure (Definition 7.17) of nonforking, but we will not pursue it here).

Definition 7.15.

1. 1. Let $\lambda $ be a cardinal. An independence relation has the $\lambda $ -witness property if the following holds: let a be a singleton and $M,N\in K$ . If for any $M'$ with $M\leq M'\leq N$ , $\Vert M' \Vert \leq \Vert M \Vert +\lambda $ , we have , then .

2. 2. An independence relation satisfies left transitivity if the following holds: let A be a set, $M_0\leq M_1\leq N$ with and , then .

Fact 7.16 [6, Theorem 7.7].

Let $\mathbf {K}$ have a monster model and an independence relation over types of arbitrary length. Suppose the independence relation satisfies: invariance, monotonicity, left transitivity, existence, extension, uniqueness, symmetry and $\operatorname {LS}(\mathbf {K})$ -witness property for singletons. For any $p\in \operatorname {gS}(M)$ , any $q\in \operatorname {gS}(M_1)$ extending p such that both $U(p),U(q)<\infty $ , then

$$ \begin{align*}U(p)=U(q)\Leftrightarrow q\text{ is a nonforking extension of }p.\end{align*} $$

We notice a gap in [6, Lemma 7.6] which Fact 7.16 depends on (readers can skip after the proof of Proposition 7.19 if they simply use Fact 7.16 as a blackbox). As usual, their definition of independence relations assume that the domain contains the base: if we write , we assume $M\leq N$ . In the proof of [6, Lemma 7.6], they applied monotonicity to obtain . However, $\bar {N_0}\not \leq N_1$ because $c\in \bar {N_0}-N_1$ might happen. We will rewrite the proof in Proposition 7.19 using the idea of a closure of an independence relation, and drawing results from [7].

Definition 7.17 [7, Definition 3.4].

is a closure of an independence relation if it satisfies the following properties:

1. 1. is defined on triples of the form $(A,M,B)$ where $M\in K$ , A and B are sets of elements. We allow $M\not \subseteq B$ .

2. 2. Invariance: if $f\in \operatorname {Aut}(\mathfrak {C})$ and , then .

3. 3. Monotonicity: if , $A'\subseteq A$ , $B'\subseteq B$ , then .

4. 4. Base monotonicity: if and $M\leq M'\subseteq M\cup B$ , then .

The minimal closure of (which is the smallest closure of ) is defined by: iff there is $N\geq M$ , $N\supseteq C$ such that .

We quote the following lemma without proof.

Lemma 7.18 [7, Lemma 5.4].

Let be an independence relation for types of arbitrary length, be the minimal closure of .

1. 1. has symmetry iff has symmetry.

2. 2. Suppose has existence, extension. Then has left transitivity iff does.

Proposition 7.19. Under the same hypothesis as Fact 7.10, let $N_0\leq N_1\leq \bar {N_1}$ ; $N_0\leq \bar {N_0}\leq \bar {N_1}$ ; $N_0\leq N_2$ ; $c\in |N_0|$ . If

then there is some $N_3$ extending both $N_1$ and $N_2$ such that

Proof We write

to mean the minimal closure of the given independence relation

. By symmetry twice on

, there is $\bar {N_2}$ containing c and extending $\bar {N_0},N_2$ such that

. By definition of the minimal closure,

On the other hand, by symmetry (and monotonicity) on

,

. Then

. Applying Lemma 7.18(2) to the last two closure independence, we have

. By Lemma 7.18(1), there is $N_3'\geq N_2$ and containing c such that

. By definition of the minimal closure,

. (Here we return to the original proof.) By base monotonicity,

. By symmetry, there is $N_3$ extending $N_1$ and $N_2$ such that

. By monotonicity,

as desired.

Back to Fact 7.16, we would like to know if there are any examples of independence relations that satisfy its hypotheses. The approach in [6] is to consider coheir [6, Definition 3.2], assuming tameness, shortness, no weak order property and that coheir satisfies extension. More developments of coheir can be found in [32] but the framework there is too abstract to handle. Another natural candidate is $\mu $ -nonforking. The obstacle is that the hypotheses require the independence relation to be over types of arbitrary length, so the properties required (say symmetry) are stronger. In the following, we will use known results to extend $\mu $ -nonforking to longer types.

We state the full assumptions of the following facts.

Fact 7.20. Let $\mathbf {K}$ have a monster model, $\lambda \geq \operatorname {LS}(\mathbf {K})$ .

1. 1. [12, Theorem 1.1] Suppose $\mathbf {K}$ is $\lambda $ -tame and there is a good $(\geq \lambda )$ -frame perhaps except the symmetry property. Then the frame can be extended to a good frame for types of arbitrary length and satisfying symmetry.

2. 2. [7, Lemma 5.9] Let be an independence relation for types of arbitrary length. Suppose satisfies symmetry and right transitivity, then it satisfies left transitivity.

Remark 7.21.

1. 1. The way that [12, Definition 4.1] extends a good frame to longer types is via “independent sequences.” In general the extended frame is not necessarily type-full (existence holds for independent sequences only). However, our original $\mu $ -nonforking for singletons is type-full and we start from singletons as input for the U-rank, so our argument goes through.

2. 2. If we simply extend nonsplitting of singletons to nonsplitting of longer types (allowing $p\in \operatorname {gS}^{<\infty }(N)$ in Definition 3.2), then it changes the definition of nonforking and many results do not generalize (stability of $\mu $ -types in $K_{\mu }$ immediately fails).

We can now derive an independence relation that satisfies the hypotheses of Fact 7.16 under $\mu $ -superstability. We will use Assumption 2.1.

Proposition 7.22. Let $\mathbf {K}$ be $\mu $ -superstable. Let $\mathbf {K'}$ be the AEC of the limit models in $K_{\geq \mu }$ ordered by $\leq _u$ . Then $\mu $ -nonforking restricted to $\mathbf {K'}$ can be extended to a good frame for types of arbitrary length. Also it satisfies left transitivity and $\mu $ -witness property for singletons.

Proof By Corollary 4.13 and Remark 4.14(2), $\mu $ -nonforking restricted to $\mathbf {K'}$ forms a good ( $\geq \mu $ )-frame perhaps except symmetry (it actually satisfies symmetry by Corollary 5.13(2) but we do not need this result here). $\mathbf {K'}$ is also $\mu $ -tame because $\mathbf {K}$ is $\mu $ -tame under Assumption 2.1 and we can extend a model in $K_{\mu }$ to a limit model which is in $K'$ . By Fact 7.20(1), $\mu $ -nonforking can be extended to a good $(\geq \mu )$ -frame for types of arbitrary length.

Since the extended frame enjoys symmetry and right transitivity, by Fact 7.20(2) it satisfies left transitivity. We check the $\mu $ -witness property for singletons: let $M\leq _uN$ both in $K'$ , $p\in \operatorname {gS}(N)$ . Suppose for any $M'$ with $M\leq _u M'\leq _u N$ , $\Vert M' \Vert \leq \Vert M \Vert +\mu =\Vert M \Vert $ , we have $p\restriction N'$ does not $\mu $ -fork over M. We need to show that p does not $\mu $ -fork over M. Without loss of generality assume $\Vert N \Vert>\Vert M \Vert $ . By existence of $\mu $ -nonsplitting (Proposition 3.12), there is $N'\in K$ , $N'\leq N$ such that p does not $\mu $ -split over $N'$ . As N is saturated (replace “ $\mu $ ” by $\Vert N \Vert $ in Corollary 6.2(2)), we can obtain $N"\in K^{\prime }_{\Vert M \Vert }$ such that $N'<_uN"<_uN$ and $M\leq _uN"$ . By definition p does not $\mu $ -fork over $N"$ . Since $p\restriction N"$ does not $\mu $ -fork over M by assumption, Corollary 4.8 guarantees that p does not $\mu $ -fork over M.

Corollary 7.23. Let $\mathbf {K}$ be $\mu $ -superstable, and let $\mathbf {K'}$ be the AEC of the limit models in $K_{\geq \mu }$ ordered by $\leq _u$ . Let be the extended frame from Proposition 7.22 and define the U-rank for . For any $M<_uM_1\in K'$ , $p\in \operatorname {gS}(M)$ , any $q\in \operatorname {gS}(M_1)$ extending p such that both $U(p),U(q)<\infty $ , then

$$ \begin{align*}U(p)=U(q)\Leftrightarrow q\text{ is a nonforking extension of }p.\end{align*} $$

Proof Combine Fact 7.16 and Proposition 7.22.

8 The main theorems and applications

We summarize our results in two main theorems. The first one concerns stable AECs while the second one concerns superstable ones. Some of the following items allow $\mu \geq \operatorname {LS}(\mathbf {K})$ but we assume $\mu>\operatorname {LS}(\mathbf {K})$ for a uniform statement. The proofs will come after the main theorems.

Main Theorem 8.1. Let $\mathbf {K}$ be an AEC with a monster model, $\mu>\operatorname {LS}(\mathbf {K})$ , $\delta \leq \mu $ both be regular. Suppose $\mathbf {K}$ is $\mu $ -tame, stable in $\mu $ and has continuity of $\mu $ -nonsplitting. The following statements are equivalent under extra assumptions specified after the list:

1. 1. $\mathbf {K}$ has $\delta $ -local character of $\mu $ -nonsplitting.

2. 2. There is a good frame over the skeleton of $(\mu ,\geq \delta )$ -limit models ordered by $\leq _u$ , except for symmetry and local character $\delta $ in place of ${\aleph _0}$ . In this case the frame is canonical.

3. 3. $\mathbf {K}$ has uniqueness of $(\mu ,\geq \delta )$ -limit models.

4. 4. For any increasing chain of $\mu ^+$ -saturated models, if the length of the chain has cofinality $\geq \delta $ , then the union is also $\mu ^+$ -saturated.

5. 5. $K_{\mu ^+}$ has a $\delta $ -superlimit.

(1) and (2) are equivalent. If $\mathbf {K}$ is $(<\mu )$ -tame, then (3) implies (1). There is $\lambda _1<h(\mu )$ such that if $\mathbf {K}$ is stable in $[\mu ,\lambda _1)$ , then (1) implies (3). Given any $\zeta \geq \mu ^+$ , stability in $[\mu ,\lambda _1)$ can be replaced by stability in $[\mu ,\zeta )$ plus no $\mu $ -order property of length $\zeta $ .

There is $\lambda _2<h(\mu ^+)$ such that if $\mathbf {K}$ is stable in $[\mu ^+,\lambda _2)$ and has continuity of $\mu ^+$ -nonsplitting, then (1) implies (4). Given any $\zeta \geq \mu ^{++}$ , stability in $[\mu ^+,\lambda _2)$ can be replaced by stability in $[\mu ^+,\zeta )$ plus no $\mu ^+$ -order property of length $\zeta $ . Always (4) and (5) are equivalent and they imply (3).

The following diagram summarizes the implications in Main Theorem 8.1. Labels on the arrows indicate the extra assumptions needed, in addition to a monster model, $\mu $ -tameness, stability in $\mu $ and continuity of $\mu $ -nonsplitting. As in the theorem statement, whenever we require stability in the form $[\xi ,\lambda )$ , we can replace it by stability in $[\xi ,\zeta )$ plus no $\xi $ -order property of length $\zeta $ .

Main Theorem 8.2. Let $\mathbf {K}$ be an AEC with a monster model, $\mu>\operatorname {LS}(\mathbf {K})$ and $\delta $ be a regular cardinal $\leq \mu $ . Suppose $\mathbf {K}$ is $\mu $ -tame, stable in $\mu $ and has continuity of $\mu $ -nonsplitting. The following statements are equivalent modulo $(<\mu )$ -tameness and a jump in cardinal (specified after the list):

1. 1. $\mathbf {K}$ has ${\aleph _0}$ -local character of $\mu $ -nonsplitting.

2. 2. There is a good frame over the limit models in $K_{\mu }$ ordered by $\leq _u$ , except for symmetry. In this case the frame is canonical.

3. 3. $K_{\mu }$ has uniqueness of limit models.

4. 4. For any increasing chain of $\mu ^+$ -saturated models, the union of the chain is also $\mu ^+$ -saturated.

5. 5. $K_{\mu ^+}$ has a superlimit.

6. 6. $\mathbf {K}$ is $(\mu ^+,\mu ^+)$ -solvable.

7. 7. $\mathbf {K}$ is stable in $\geq \mu $ and has continuity of $\mu ^{+\omega }$ -nonsplitting.

8. 8. U-rank is bounded when $\mu $ -nonforking is restricted to the limit models in $K_{\mu }$ ordered by $\leq _u$ .

(1), (2), and (8) are equivalent and each of them implies (3) and (4). If $\mathbf {K}$ is $(<\mu )$ -tame, then (3) implies (1). Always (4) and (5) are equivalent and they imply (3). (1) implies (6) and (7) while (6) implies (4). (7) implies $(1)_{\mu ^{+\omega }}$ : $\mathbf {K}$ has ${\aleph _0}$ -local character of $\mu ^{+\omega }$ -nonsplitting.

The jump in cardinal is due to the lack of a precise bound on $\lambda '(\mathbf {K})$ in deducing (7) $\Rightarrow $ (1) (see Question 7.8(1)). The following diagram summarizes the implications in Main Theorem 8.2. “ $\mu ^{+\omega }$ ” indicates the jump in cardinal.

Proof of Main Theorem 8.1

(1) and (2) are equivalent by Corollary 4.13 and Proposition 4.19. The canonicity of the frame is by Proposition 4.18. Suppose (3) holds. Then the proof of Corollary 6.2(2) and Proposition 6.12(1) give (1).

Suppose (1) holds. Obtain $\lambda _1=\lambda $ from Corollary 6.2 and take $\chi =\delta $ . If $\mathbf {K}$ is stable in $[\mu ,\lambda _1)$ , then it has uniqueness of $(\mu ,\geq \delta )$ -limit models, so (3) holds. The alternative hypotheses of stability and no-order-property work because we can replace $\lambda $ in the proof of Proposition 5.9 by $\zeta $ .

The direction of (1)–(4) is by Proposition 6.6. The alternative hypotheses work because we can replace $\lambda $ in the proof of Proposition 5.9 by $\zeta $ . (4) and (5) are equivalent by Lemma 6.22 and Lemma 6.23. They imply (3) by Corollary 6.16.

For the proof of Main Theorem 8.2, we show the additional directions and refer the readers to the proof of Main Theorem 8.1 for the original directions.

Proof of Main Theorem 8.2

Compared to Main Theorem 8.1, we do not need the extra stability and continuity of nonsplitting assumptions because superstability already implies them (Corollary 6.11(1) and Proposition 3.16(1)). (1) and (8) are equivalent by Corollary 7.14. (1) implies (7) by Corollary 6.11(1) while (1) implies (6) by the forward direction of Proposition 6.24(2). (6) plus $(<\mu )$ -tameness implies (4) by the proof of the backward direction of Proposition 6.24(2). (7) implies $(1)_{\mu ^{+\omega }}$ by Proposition 7.5.

Remark 8.3. In [18, Corollary 5.5], they did not assume continuity of nonsplitting and showed that: if item (4) in Main Theorem 8.2 holds for $\mu \geq \beth _\omega (\chi _0+\mu )$ (see Fact 6.3 for the definition of $\chi _0$ ), then every limit model in $K_{\mu ^+}$ is $\beth _\omega (\chi _0+\mu )$ -saturated. This implies ${\aleph _0}$ -local character of $\mu ^+$ -nonsplitting. Using [12, Theorem 7.1], there is a $\lambda <h(\mu ^+)$ such that (3) holds with $\mu $ replaced by $\lambda $ . From hindsight, the last argument can be improved by quoting Corollary 6.11(3) instead and having $\lambda =\mu ^{++}$ . In comparison, our (4) $\Rightarrow $ (3) allows (3) to still be in $K_{\mu }$ and does not have the high cardinal threshold.

Corollary 8.4. Let $\xi>\operatorname {LS}(\mathbf {K})$ and $\mathbf {K}$ have a monster model, continuity of $\xi $ -nonsplitting and be $(<\xi )$ -tame. Then the following are equivalent:

1. 1. $\mathbf {K}$ has uniqueness of limit models in $K_\xi $ : for any $M_0,M_1,M_2\in K_\xi $ , if both $M_1$ and $M_2$ are limit over $M_0$ , then $M_1\cong _{M_0}M_2$ .

2. 2. $\mathbf {K}$ has uniqueness of limit models without base in $K_\xi $ : any limit models in $K_\xi $ are isomorphic.

Proof The forward direction is immediate and only requires $JEP$ . For the backward direction, the proof of (3) $\Rightarrow $ (1) in Main Theorem 8.2 goes through ( $JEP$ is needed) and we have $\xi $ -superstability. By (1) $\Rightarrow $ (3) in Main Theorem 8.2, it has uniqueness of limit models in $K_\xi $ .

As applications, we present alternative proofs to the results in [21, 25] with stronger assumptions. In [21], limit models of abelian groups are studied.

Fact 8.5.

1. 1. [21, Definition 3.1 and Fact 3.2] Let $\mathbf {K}^{ab}$ be the class of abelian groups ordered by subgroup relation. Then $\mathbf {K}^{ab}$ is an AEC with $\operatorname {LS}(\mathbf {K}^{ab})={\aleph _0}$ , has a monster model and is $(<{\aleph _0})$ -tame.

2. 2. [21, Fact 3.3(2)] $\mathbf {K}^{ab}$ is stable in all infinite cardinals.

3. 3. [21, Corollary 3.8] $\mathbf {K}^{ab}$ has uniqueness of limit models in all infinite cardinals.

In the original proof of Fact 8.5(3), an explicit algebraic expression of limit models was obtained, so that limit models of the same cardinality are isomorphic to each other. In [21, Remark 3.9], it was remarked that [38] could be used to obtain uniqueness of limit models for high enough cardinals (above $\geq \beth _{(2^{{\aleph _0}})^+}$ ). We write down the exact argument using known results. Then we present another proof that covers lower cardinals using results in this paper (but not any algebraic description of limit models).

First proof of Fact 8.5(3).

In Fact 7.4(1), pick $\xi \geq (\lambda '(\mathbf {K}))^++\chi _1$ with $\operatorname {cf}(\xi )={\aleph _0}$ . By Fact 8.5(2), $\mathbf {K}^{ab}$ is stable in $\xi $ . So the conclusion of Fact 7.4(1) gives superstability in $\geq \lambda '(\mathbf {K}^{ab})$ . By [31, Corollary 1.4] (which combines [31, Fact 2.16 and Corollary 6.9]), $\mathbf {K}^{ab}$ has uniqueness of limit models in $K^{ab}_{\geq \lambda '(\mathbf {K}^{ab})}$ . Notice that by Fact 7.3, $\lambda '( \mathbf {K}^{ab})<h(\lambda (\mathbf {K}^{ab}))=h({\aleph _0})=\beth _{(2^{{\aleph _0}})^+}$ , so we can guarantee uniqueness of limit models above $\beth _{(2^{{\aleph _0}})^+}$ .

Second proof of Fact 8.5(3).

By Fact 8.5(1)(2), $\mathbf {K}^{ab}$ is stable in ${\aleph _0}$ and is $(<{\aleph _0})$ -tame. The latter implies $\omega $ -locality. By Proposition 3.16(2), $\mathbf {K}^{ab}$ has continuity of ${\aleph _0}$ -nonsplitting. By Remark 7.7(1), it is superstable in $\geq {\aleph _0}$ . By Corollary 6.2(1) (or simply [31, Corollary 1.4]), it has uniqueness of limit models in all infinite cardinals.

We turn to look at a strictly stable AEC.

Fact 8.6.

1. 1. [21, Definition 4.1 and Facts 4.2 and 4.5] Let $\mathbf {K}^{tf}$ be the class of torsion-free abelian groups ordered by pure subgroup relation. Then $\mathbf {K}^{tf}$ is an AEC with $\operatorname {LS}(\mathbf {K}^{tf})={\aleph _0}$ , has a monster model and is $(<{\aleph _0})$ -tame.

2. 2. [21, Fact 4.7] $\mathbf {K}^{tf}$ is stable in $\lambda $ iff $\lambda ^{{\aleph _0}}=\lambda $ . In particular $\mathbf {K}^{tf}$ is strictly stable.

3. 3. [21, Corollary 4.18] Let $\lambda \geq \aleph _1$ . $\mathbf {K}^{tf}$ has uniqueness of $(\lambda ,\geq \aleph _1)$ -limit models.

4. 4. [21, Theorem 4.22] Let $\lambda \geq {\aleph _0}$ . Any $(\lambda ,{\aleph _0})$ -limit model in $\mathbf {K}^{tf}$ is not algebraically compact.

5. 5. [21, Lemmas 4.10 and 4.14] Let $\lambda \geq \aleph _1$ . Any $(\lambda ,\geq \aleph _1)$ -limit model in $\mathbf {K}^{tf}$ is algebraically compact. Any two algebraically compact limit models in $K^{tf}_\lambda $ are isomorphic.

The original proof of the second part of Fact 8.6(3) uses an explicit algebraic expression of algebraically compact groups [21, Fact 4.13]. Using the results of this paper, we give a weaker version but without using any algebraic expression of algebraically compact groups.

Proposition 8.7. Assume CH. If $\mathbf {K}^{tf}$ does not have $\aleph _1$ -order property of length $\aleph _\omega $ , then for all $\lambda \geq \aleph _1$ , it has uniqueness of $(\lambda ,\geq \aleph _1)$ -limit models.

Proof By CH and Fact 8.6(2), $\mathbf {K}^{tf}$ is stable in $\aleph _1$ . By Fact 8.6(1), $\mathbf {K}^{tf}$ is $(<{\aleph _0})$ -tame, hence it has $\omega $ -locality. By Proposition 3.16(2), $\mathbf {K}^{tf}$ has continuity of $\lambda $ -nonsplitting for all $\lambda \geq \aleph _1$ . Proposition 3.9 and Lemma 6.7 give $\aleph _1$ -local character of $\lambda $ -nonsplitting for all $\lambda \geq \aleph _1$ . By Fact 6.10(1), $\mathbf {K}^{tf}$ is stable in $[\aleph _1,\aleph _\omega )$ . By Corollary 6.2(1) and Remark 6.8(1), $\mathbf {K}^{tf}$ has uniqueness of $(\lambda ,\geq \aleph _1)$ -limit models for all $\lambda \geq \aleph _1$ .

Question 8.8. Is it true that $\mathbf {K}^{tf}$ does not have $\aleph _1$ -order property of length $\aleph _\omega $ ?

For Fact 8.6(4), the original proof argued that uniqueness of limit models eventually leads to superstability for large enough $\lambda $ (from an older result in [18]). Then a specific construction deals with small $\lambda $ . In [21, Remark 4.23], it was noted that [38, Lemma 4.12] could deal with both cases of $\lambda $ . We give a full proof here (the algebraic description of limit models is needed):

Proof of Fact 8.6(4)

Let $\lambda \geq {\aleph _0}$ and M be a $(\lambda ,{\aleph _0})$ -limit model. Then $\mathbf {K}^{tf}$ is stable in $\lambda $ and by Fact 8.6(2) $\lambda>{\aleph _0}$ . Suppose M is algebraically compact, by Fact 8.6(5) and Corollary 6.2(2) M is isomorphic to $(\lambda ,\geq \aleph _1)$ -limit models and is saturated. By Proposition 6.12(3) (where $\langle M_i:i\leq {\aleph _0}\rangle $ witnesses that M is $(\lambda ,{\aleph _0})$ -limit), ${\aleph _0}$ -local character of $\lambda $ -nonsplitting applies to M. Since M is arbitrary, $\mathbf {K}^{tf}$ has ${\aleph _0}$ -local character of $\lambda $ -nonsplitting, which implies stability in $\geq \lambda $ by Fact 6.10(2), contradicting Fact 8.6(2).

Remark 8.9. [38, Lemma 4.12] happened to work because we do not care about the case ${\aleph _0}$ (which is not stable) and we can always apply item (3) in Proposition 6.12.

In [25], $\aleph _0$ -stable AECs with ${\aleph _0}$ - $AP$ , ${\aleph _0}$ - $JEP,$ and ${\aleph _0}$ - $NMM$ were studied. They built a superlimit model in ${\aleph _0}$ by connecting limit models with sequentially homogeneous models [25, Theorem 4.4]. Then they defined splitting over finite sets where types have countable domains and obtained finite character assuming categoricity in ${\aleph _0}$ [25, Fact 5.3]. This allowed them to build a good ${\aleph _0}$ -frame over models generated by the superlimit. These methods are absent in our paper because we studied AECs with a general $\operatorname {LS}(\mathbf {K})$ , and our splitting is defined for types of model-domains.

In [25, Corollary 5.9], they showed the existence of a superlimit in $\aleph _1$ assuming weak $(<{\aleph _0},{\aleph _0})$ -locality among other assumptions. We will strengthen the locality assumption to $\omega $ -locality, and work in a monster model to give an alternative proof. This allows us to bypass the machineries in [25] that are sensitive to the cardinal ${\aleph _0}$ , and the technical manipulation of symmetry in [25, Section 3]. Also, our result extends to a general $\operatorname {LS}(\mathbf {K})$ .

Proposition 8.10. Let $\mathbf {K}$ is an ${\aleph _0}$ -stable AEC with a monster model and has $\omega $ -locality. Then there is a superlimit in $\aleph _1$ . In general, let $\lambda \geq \operatorname {LS}(\mathbf {K})$ , and if $\mathbf {K}$ is stable in $\lambda $ instead of ${\aleph _0}$ , then it has a superlimit in $\lambda ^+$ .

Proof Apply Main Theorem 8.2(1) $\Rightarrow $ (5) where $\mu =\operatorname {LS}(\mathbf {K})$ (that direction does not require $\mu>\operatorname {LS}(\mathbf {K})$ ). Notice that $\omega $ -locality implies $\operatorname {LS}(\mathbf {K})$ -tameness.

Tracing our proof, we require global assumptions of a monster model and $\omega $ -locality in order to use our symmetry results, especially Proposition 5.9. We end this section with the following:

Question 8.11. Instead of global assumptions like monster model and no-order-property, is it possible to obtain local symmetry properties in Section 5 using more local assumptions?