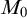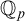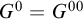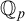Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
ITERATION THEOREMS FOR SUBVERSIONS OF FORCING CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1-51
-
- Article
- Export citation
A NOTE ON THE NON-EXISTENCE OF PRIME MODELS OF THEORIES OF PSEUDO-FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 03 March 2025, pp. 52-67
-
- Article
- Export citation
DIMENSION AND MEASURE IN PSEUDOFINITE H-STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2025, pp. 68-104
-
- Article
- Export citation
COLORING ISOSCELES TRIANGLES IN CHOICELESS SET THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 11 September 2023, pp. 105-134
-
- Article
- Export citation
ON PROVING CONSISTENCY OF EQUATIONAL THEORIES IN BOUNDED ARITHMETIC
- Part of:
-
- Published online by Cambridge University Press:
- 27 January 2025, pp. 135-165
-
- Article
- Export citation
WEAK HEIRS, COHEIRS, AND THE ELLIS SEMIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2023, pp. 166-187
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTABLE TOPOLOGICAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 18 September 2023, pp. 188-220
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON EQUIVALENCE RELATIONS INDUCED BY LOCALLY COMPACT ABELIAN POLISH GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2023, pp. 221-236
-
- Article
- Export citation
COFINALITY QUANTIFIERS IN ABSTRACT ELEMENTARY CLASSES AND BEYOND
- Part of:
-
- Published online by Cambridge University Press:
- 26 May 2023, pp. 237-251
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COVERING NUMBERS OF SOME MYCIELSKI IDEALS MAY BE DIFFERENT
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2025, pp. 252-277
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A TERMINATING INTUITIONISTIC CALCULUS
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2023, pp. 278-297
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUSLIN TREE PRESERVATION AND CLUB ISOMORPHISMS
- Part of:
-
- Published online by Cambridge University Press:
- 22 December 2022, pp. 298-309
-
- Article
- Export citation
A TOPOMETRIC EFFROS THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2023, pp. 310-320
-
- Article
- Export citation
HYBRID PARTIAL TYPE THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2023, pp. 321-363
-
- Article
- Export citation
ON A CONJECTURE REGARDING THE MOUSE ORDER FOR WEASELS
- Part of:
-
- Published online by Cambridge University Press:
- 17 March 2025, pp. 364-390
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEMI-EQUATIONAL THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2023, pp. 391-422
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISCRETE SETS DEFINABLE IN STRONG EXPANSIONS OF ORDERED ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2024, pp. 423-459
-
- Article
-
- You have access
- HTML
- Export citation
ABELIAN GROUPS DEFINABLE IN p-ADICALLY CLOSED FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2023, pp. 460-481
-
- Article
- Export citation
JSL volume 90 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 10 April 2025, pp. f1-f3
-
- Article
-
- You have access
- Export citation
JSL volume 90 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 10 April 2025, pp. b1-b2
-
- Article
-
- You have access
- Export citation

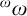
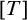

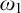








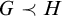
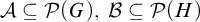
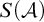

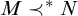
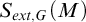
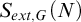
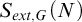
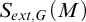

























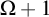



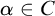
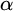
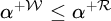
 -Woodin cardinal. On the other hand, we show that assuming there is no transitive model of KP with a Woodin cardinal the conjecture holds. In the course of this we will also show that if
-Woodin cardinal. On the other hand, we show that assuming there is no transitive model of KP with a Woodin cardinal the conjecture holds. In the course of this we will also show that if