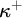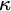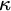0 Introduction
0.1 Intermediate models of the tree-Prikry forcing
In many mathematical theories, such as groups, vector spaces, topological spaces, and graphs, the study of submodels of a given model is indispensable to the understanding of the model and in some sense measures its complexity. In forcing theory, subforcings of a given forcing generate intermediate models to a generic extension by the forcing. Hence, the study of intermediate models is somehow parallel to the one regarding subforcings. There are numerous classification results in this spirit, for example, some forcing such as the Sacks forcing [Reference Sacks34] and variants of the tree-Prikry forcing [Reference Koepke, Rasch and Schlicht25] do not have proper intermediate models. Other forcings such as the Cohen forcing [Reference Kanamori24], Random forcing [Reference Maharam27], Prikry forcing [Reference Gitik, Kanovei and Koepke20], and Magidor forcing [Reference Benhamou and Gitik6, Reference Benhamou and Gitik8] have intermediate models of the same type. A tree-Prikry forcing or its particular case, which will be central for us in this paper, the Prikry forcing with a non-normal ultrafilter can behave differently. For example, under suitable large cardinal assumptions, every
![]() $\kappa $
-distributive forcing of cardinality
$\kappa $
-distributive forcing of cardinality
![]() $\kappa $
is a projection of this forcing. Actually, more is true, under the assumption that
$\kappa $
is a projection of this forcing. Actually, more is true, under the assumption that
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa $
-compact there is a single Prikry-type forcing which absorbs all the
$\kappa $
-compact there is a single Prikry-type forcing which absorbs all the
![]() $\kappa $
-distributive forcings of cardinality
$\kappa $
-distributive forcings of cardinality
![]() $\kappa $
(see [Reference Gitik19]). In the absence of very large cardinals, the situation changes; indeed, Hayut and the authors [Reference Benhamou, Gitik and Hayut9] proved that if a certain
$\kappa $
(see [Reference Gitik19]). In the absence of very large cardinals, the situation changes; indeed, Hayut and the authors [Reference Benhamou, Gitik and Hayut9] proved that if a certain
![]() $<\kappa $
-strategically closed forcing of cardinality
$<\kappa $
-strategically closed forcing of cardinality
![]() $\kappa $
is a projection of the tree-Prikry forcing then it is consistent that there is a cardinal
$\kappa $
is a projection of the tree-Prikry forcing then it is consistent that there is a cardinal
![]() $\lambda $
with high Mitchell order, namely
$\lambda $
with high Mitchell order, namely
![]() $o(\lambda )>\lambda ^+$
. In [Reference Benhamou and Gitik6], the authors proved that starting from a measurable cardinal (which is the minimal large cardinal assumption in the context of Prikry forcing) it is consistent that there is a (non-normal) ultrafilter U, such that the Prikry forcing with U projects onto the Cohen forcing
$o(\lambda )>\lambda ^+$
. In [Reference Benhamou and Gitik6], the authors proved that starting from a measurable cardinal (which is the minimal large cardinal assumption in the context of Prikry forcing) it is consistent that there is a (non-normal) ultrafilter U, such that the Prikry forcing with U projects onto the Cohen forcing
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,1)$
; this was improved later in [Reference Benhamou, Gitik and Hayut9] to a larger class of forcing notions called Masterable forcings. In the context of Prikry-type forcings, the existence of such embeddings and projections allows one to iterate distributive forcing notions on different cardinals (see [Reference Gitik, Foreman and Kanamori17, Section 6.4]).
$\operatorname {\mathrm {Cohen}}(\kappa ,1)$
; this was improved later in [Reference Benhamou, Gitik and Hayut9] to a larger class of forcing notions called Masterable forcings. In the context of Prikry-type forcings, the existence of such embeddings and projections allows one to iterate distributive forcing notions on different cardinals (see [Reference Gitik, Foreman and Kanamori17, Section 6.4]).
It remained open whether it is possible to get more Cohen subsets of
![]() $\kappa $
after forcing with the Prikry forcing with a
$\kappa $
after forcing with the Prikry forcing with a
![]() $\kappa $
-complete ultrafilter U over
$\kappa $
-complete ultrafilter U over
![]() $\kappa $
. This was asked explicitly in [Reference Benhamou, Gitik and Hayut9].
$\kappa $
. This was asked explicitly in [Reference Benhamou, Gitik and Hayut9].
The basic difficulty is that the size of
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
is
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
is
![]() $\kappa ^+$
and it is not hard to see (Proposition 2.9) that this cannot happen, if U has the Galvin property.
$\kappa ^+$
and it is not hard to see (Proposition 2.9) that this cannot happen, if U has the Galvin property.
We formulate a certain strengthening of the negation of the Galvin property, show its consistency starting with a measurable cardinal, and finally apply it in order to construct an ultrafilter U such that the Prikry forcing (for a formal definition of the Prikry forcing with non-normal ultrafilter, see Definition 1.2) with it adds a generic subset to
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
.
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
.
0.2 Extender-based Prikry forcing and a question of Woodin
Magidor and the second author developed the Extender-based Prikry forcing in [Reference Gitik and Magidor21] to violate the SCH under mild large cardinal assumptions. Later Merimovich [Reference Merimovich29, Reference Merimovich30] presented a variation of this forcing which will be used in this paper.
H. Woodin askedFootnote
1
in the early
![]() $90$
s whether, assuming that there is no inner model with a strong cardinal, it is possible to have a model M in which
$90$
s whether, assuming that there is no inner model with a strong cardinal, it is possible to have a model M in which
![]() $2^{\aleph _\omega }\geq \aleph _{\omega +3}$
, GCH holds below
$2^{\aleph _\omega }\geq \aleph _{\omega +3}$
, GCH holds below
![]() $\aleph _\omega $
, there is an inner model N such that
$\aleph _\omega $
, there is an inner model N such that
![]() $\kappa =(\aleph _\omega )^M$
is a measurable and
$\kappa =(\aleph _\omega )^M$
is a measurable and
![]() $2^{\kappa }\geq (\aleph _{\omega +3})^M$
.
$2^{\kappa }\geq (\aleph _{\omega +3})^M$
.
A natural approach to tackle Woodin’s question is to use the Extender-based Prikry with interleaved collapses forcing, defined by the second author and Magidor in [Reference Gitik and Magidor21]. This forcing collapses a measurable cardinal to
![]() $\aleph _\omega $
and simultaneously blows up the powerset of that measurable. Hence, if one can show that a generic extension by the Extender-based Prikry forcing has an intermediate model where
$\aleph _\omega $
and simultaneously blows up the powerset of that measurable. Hence, if one can show that a generic extension by the Extender-based Prikry forcing has an intermediate model where
![]() $\kappa $
stays measurable and
$\kappa $
stays measurable and
![]() $2^{\kappa }$
is large, this will provide a positive answer to Woodin’s question. In this paper we show that this approach is doomed. More precisely, we address in general the question whether it is possible to add many subsets of
$2^{\kappa }$
is large, this will provide a positive answer to Woodin’s question. In this paper we show that this approach is doomed. More precisely, we address in general the question whether it is possible to add many subsets of
![]() $\kappa \ {\langle } x_\alpha \mid \alpha <\lambda {\rangle }, \ \lambda \geq \kappa ^{++}$
with the Extender-based Prikry forcing over
$\kappa \ {\langle } x_\alpha \mid \alpha <\lambda {\rangle }, \ \lambda \geq \kappa ^{++}$
with the Extender-based Prikry forcing over
![]() $ \kappa $
such that
$ \kappa $
such that
![]() $\kappa $
remains a regular cardinal in
$\kappa $
remains a regular cardinal in
![]() $V[ {\langle } x_\alpha \mid \alpha <\lambda {\rangle }]$
. We give a negative answer to this question with respect to the Extender-based Prikry forcing as defined in [Reference Gitik and Magidor21] and the Merimovich version of the forcing presented in [Reference Merimovich30, Reference Merimovich31]. In particular, as a consequence of our results (Theorems 4.5 and 4.6), the Extender-based Prikry forcing cannot be used to answer Woodin’s question.
$V[ {\langle } x_\alpha \mid \alpha <\lambda {\rangle }]$
. We give a negative answer to this question with respect to the Extender-based Prikry forcing as defined in [Reference Gitik and Magidor21] and the Merimovich version of the forcing presented in [Reference Merimovich30, Reference Merimovich31]. In particular, as a consequence of our results (Theorems 4.5 and 4.6), the Extender-based Prikry forcing cannot be used to answer Woodin’s question.
0.3 The Galvin property
F. Galvin [Reference Baumgartner, Ha̧jņal and Mate2], in the 70s, showed that if
![]() $\kappa ^{<\kappa }=\kappa $
and F is a normal filter over
$\kappa ^{<\kappa }=\kappa $
and F is a normal filter over
![]() $\kappa $
then the following combinatorial property holds:
$\kappa $
then the following combinatorial property holds:
We denote this statement by
![]() $Gal(F,\kappa ,\kappa ^+)$
. In particular, this holds for the club filter
$Gal(F,\kappa ,\kappa ^+)$
. In particular, this holds for the club filter
![]() $Cub_{\kappa }$
as it is a normal filter over a cardinal
$Cub_{\kappa }$
as it is a normal filter over a cardinal
![]() $\kappa $
.
$\kappa $
.
In [Reference Abraham and Shelah1], Abraham and Shelah constructed a model where
![]() $ Gal(Cub_{\kappa ^+},\kappa ^+,\kappa ^{++})$
fails for a regular
$ Gal(Cub_{\kappa ^+},\kappa ^+,\kappa ^{++})$
fails for a regular
![]() $\kappa $
. Garti [Reference Garti13, Reference Garti14] and later together with the first author and Poveda [Reference Benhamou, Garti and Poveda4] continued the investigation of the Galvin property for the club filter. The Galvin property for
$\kappa $
. Garti [Reference Garti13, Reference Garti14] and later together with the first author and Poveda [Reference Benhamou, Garti and Poveda4] continued the investigation of the Galvin property for the club filter. The Galvin property for
![]() $\kappa $
-complete ultrafilters over a measurable cardinal
$\kappa $
-complete ultrafilters over a measurable cardinal
![]() $\kappa $
was used recently in [Reference Benhamou and Gitik7, Reference Gitik18]. The question of failure of the Galvin property for such ultrafilters was shown to be independent. Namely, in [Reference Benhamou and Gitik7] the authors observed that in
$\kappa $
was used recently in [Reference Benhamou and Gitik7, Reference Gitik18]. The question of failure of the Galvin property for such ultrafilters was shown to be independent. Namely, in [Reference Benhamou and Gitik7] the authors observed that in
![]() $L[U]$
every
$L[U]$
every
![]() $\kappa $
-complete ultrafilter has the Galvin property, and Garti, Shelah, and the first author, starting with a supercompact cardinal, produced a model with a
$\kappa $
-complete ultrafilter has the Galvin property, and Garti, Shelah, and the first author, starting with a supercompact cardinal, produced a model with a
![]() $\kappa $
-complete ultrafilter which contains
$\kappa $
-complete ultrafilter which contains
![]() $Cub_\kappa $
and fails to satisfy the Galvin property.
$Cub_\kappa $
and fails to satisfy the Galvin property.
In Section 2, we isolate a property of sequences we call a strong witness for the failure of Galvin’s property which implies in particular the failure of Galvin’s property. This property is used in Theorem 2.6, where we start from a single measurable cardinal, and construct a model with an ultrafilter which fails to satisfy the Galvin property. This improves the initial large cardinal assumption of [Reference Benhamou, Garti and Shelah5].
Later in Theorem 2.10, we were able to slightly modify the construction of Theorem 2.6, construct an ultrafilter W and a strong witness for the failure of the Galvin property for it, which serves to glue together initial segments of functions, and obtain
![]() $\kappa ^+$
-mutually generic Cohen function on
$\kappa ^+$
-mutually generic Cohen function on
![]() $\kappa $
. This idea is generalized to longer sequences (and in turn to more Cohen functions) in Theorems 3.1 and 3.3.
$\kappa $
. This idea is generalized to longer sequences (and in turn to more Cohen functions) in Theorems 3.1 and 3.3.
Our main results are:
Theorem 2.6. Assume GCH and let
![]() $\kappa $
be measurable in V. Then there is a cofinality preserving forcing extension
$\kappa $
be measurable in V. Then there is a cofinality preserving forcing extension
![]() $V^*$
in which there is a
$V^*$
in which there is a
![]() $\kappa $
-complete ultrafilter W over
$\kappa $
-complete ultrafilter W over
![]() $\kappa $
which concentrates on regulars, extends
$\kappa $
which concentrates on regulars, extends
![]() $Cub_\kappa $
, and has a strong witness for the failure of Galvin’s property.
$Cub_\kappa $
, and has a strong witness for the failure of Galvin’s property.
Theorem 2.10. Assume
![]() $GCH$
and that
$GCH$
and that
![]() $\kappa $
is a measurable cardinal in V. Then there is a cofinality preserving forcing extension
$\kappa $
is a measurable cardinal in V. Then there is a cofinality preserving forcing extension
![]() $V^*$
in which
$V^*$
in which
![]() $GCH$
still holds, and there is a
$GCH$
still holds, and there is a
![]() $\kappa $
-complete ultrafilter
$\kappa $
-complete ultrafilter
![]() $U^*\in V^*$
over
$U^*\in V^*$
over
![]() $\kappa $
such that forcing with Prikry forcing
$\kappa $
such that forcing with Prikry forcing
![]() $Prikry(U^*)$
introduces a
$Prikry(U^*)$
introduces a
![]() $V^*$
-generic filter for
$V^*$
-generic filter for
![]() $Cohen^{V^*}(\kappa ,\kappa ^+)$
.
$Cohen^{V^*}(\kappa ,\kappa ^+)$
.
Theorem 3.1. Assume GCH and that there is a
![]() $(\kappa ,\kappa ^{++})$
-extender over
$(\kappa ,\kappa ^{++})$
-extender over
![]() $\kappa $
in V. Then there is a cofinality preserving forcing extension
$\kappa $
in V. Then there is a cofinality preserving forcing extension
![]() $V^*$
such that
$V^*$
such that
![]() $V^*\models 2^{\kappa }=\kappa ^{++}$
, in
$V^*\models 2^{\kappa }=\kappa ^{++}$
, in
![]() $V^*$
there is a
$V^*$
there is a
![]() $\kappa $
-complete ultrafilter W over
$\kappa $
-complete ultrafilter W over
![]() $\kappa $
which concentrates on regulars, extends
$\kappa $
which concentrates on regulars, extends
![]() $Cub_\kappa $
, and has a strong witness of length
$Cub_\kappa $
, and has a strong witness of length
![]() $\kappa ^{++}$
for the failure of Galvin’s property.
$\kappa ^{++}$
for the failure of Galvin’s property.
Theorem 3.3. Assume
![]() $GCH$
and that E is a
$GCH$
and that E is a
![]() $(\kappa ,\kappa ^{++})$
-extender in V. Then there is a cofinality preserving forcing extension
$(\kappa ,\kappa ^{++})$
-extender in V. Then there is a cofinality preserving forcing extension
![]() $V^*$
in which
$V^*$
in which
![]() $2^{\kappa }=\kappa ^{++}$
and a non-Galvin ultrafilter
$2^{\kappa }=\kappa ^{++}$
and a non-Galvin ultrafilter
![]() $W\in V^*$
such that forcing with
$W\in V^*$
such that forcing with
![]() $\operatorname {\mathrm {Prikry}}(W)$
introduces a
$\operatorname {\mathrm {Prikry}}(W)$
introduces a
![]() $V^*$
-generic filter for
$V^*$
-generic filter for
![]() $Cohen^{V^*}(\kappa ,\kappa ^{++})$
-generic filter.
$Cohen^{V^*}(\kappa ,\kappa ^{++})$
-generic filter.
Theorem 4.5. Let
![]() ${\mathcal P}_E$
be the Extender-based Prikry forcing of [Reference Gitik and Magidor21], and
${\mathcal P}_E$
be the Extender-based Prikry forcing of [Reference Gitik and Magidor21], and
![]() $G\subseteq {\mathcal P}$
be a generic. Suppose that
$G\subseteq {\mathcal P}$
be a generic. Suppose that
![]() $A\in V[G]\setminus V$
is a subset of
$A\in V[G]\setminus V$
is a subset of
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $\kappa $
changes its cofinality to
$\kappa $
changes its cofinality to
![]() $\omega $
in
$\omega $
in
![]() $V[A]$
.
$V[A]$
.
Theorem 4.6. Assume GCH, let E be an extender over
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $\mathbb {P}_E$
be the Merimovich version of the Extender-based Prikry forcing of [Reference Merimovich29–Reference Merimovich31]. Let G be a generic subset of
$\mathbb {P}_E$
be the Merimovich version of the Extender-based Prikry forcing of [Reference Merimovich29–Reference Merimovich31]. Let G be a generic subset of
![]() $\mathbb {P}_E$
and let
$\mathbb {P}_E$
and let
![]() ${\langle } {A}_\alpha \mid \alpha <\kappa ^{++} {\rangle }$
be different subsets of
${\langle } {A}_\alpha \mid \alpha <\kappa ^{++} {\rangle }$
be different subsets of
![]() $\kappa $
in
$\kappa $
in
![]() $V[G]$
. Then there is
$V[G]$
. Then there is
![]() $I\subseteq \kappa ^{++}, I\in V, |I|=\kappa $
such that
$I\subseteq \kappa ^{++}, I\in V, |I|=\kappa $
such that
![]() $\kappa $
is a singular cardinal of cofinality
$\kappa $
is a singular cardinal of cofinality
![]() $\omega $
in
$\omega $
in
![]() $V[{\langle } {A}_\alpha \mid \alpha \in I{\rangle }]$
. In particular, there is no intermediate model of
$V[{\langle } {A}_\alpha \mid \alpha \in I{\rangle }]$
. In particular, there is no intermediate model of
![]() $V[G]$
where
$V[G]$
where
![]() $\kappa $
is measurable and
$\kappa $
is measurable and
![]() $2^{\kappa }>\kappa ^+$
.
$2^{\kappa }>\kappa ^+$
.
This paper is organized as follows:
1 Basics
1.1 The forcing notions
In our notations
![]() $p\leq q$
means that q is stronger than p. We assume that the reader is familiar with the forcing method and iterated forcing. Most of our notations are inspired by [Reference Cummings, Foreman and Kanamori12, Reference Gitik, Foreman and Kanamori17] where we refer the reader for more information regarding forcing and iterations. Let us present the definitions of the forcing we intend to use:
$p\leq q$
means that q is stronger than p. We assume that the reader is familiar with the forcing method and iterated forcing. Most of our notations are inspired by [Reference Cummings, Foreman and Kanamori12, Reference Gitik, Foreman and Kanamori17] where we refer the reader for more information regarding forcing and iterations. Let us present the definitions of the forcing we intend to use:
Definition 1.1. The forcing adding
![]() $\lambda $
-many Cohen functions to
$\lambda $
-many Cohen functions to
![]() $\kappa $
denoted by
$\kappa $
denoted by
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\lambda )$
consists of all partial functions
$\operatorname {\mathrm {Cohen}}(\kappa ,\lambda )$
consists of all partial functions
![]() $f:\kappa \times \lambda \rightarrow \{0,1\}$
such that
$f:\kappa \times \lambda \rightarrow \{0,1\}$
such that
![]() $|f|<\kappa $
. The order is defined by
$|f|<\kappa $
. The order is defined by
![]() $f\leq g$
iff
$f\leq g$
iff
![]() $f\subseteq g$
.
$f\subseteq g$
.
Definition 1.2. Let U be a
![]() $\kappa $
-complete non-trivial ultrafilter over
$\kappa $
-complete non-trivial ultrafilter over
![]() $\kappa $
and let
$\kappa $
and let
![]() $\pi :\kappa \rightarrow \kappa $
be the function representing
$\pi :\kappa \rightarrow \kappa $
be the function representing
![]() $\kappa $
in the
$\kappa $
in the
![]() $\mathrm {Ult}(V,U)$
. The Prikry forcing with U, denoted by
$\mathrm {Ult}(V,U)$
. The Prikry forcing with U, denoted by
![]() $\operatorname {\mathrm {Prikry}}(U)$
, consists of all sequences
$\operatorname {\mathrm {Prikry}}(U)$
, consists of all sequences
![]() ${\langle }\alpha _1,...,\alpha _n, A{\rangle }$
such that:
${\langle }\alpha _1,...,\alpha _n, A{\rangle }$
such that:
-
(1)
 ${\langle }\alpha _1,...,\alpha _n{\rangle }$
is a
${\langle }\alpha _1,...,\alpha _n{\rangle }$
is a
 $\pi $
-increasing sequence of ordinals below
$\pi $
-increasing sequence of ordinals below
 $\kappa $
, i.e., for every
$\kappa $
, i.e., for every
 $1\leq i<n$
,
$1\leq i<n$
,
 $\alpha _i<\pi (\alpha _{i+1}),$
$\alpha _i<\pi (\alpha _{i+1}),$
-
(2)
 $A\in U$
,
$A\in U$
,
 $\pi (\min (A))>\alpha _n$
.
$\pi (\min (A))>\alpha _n$
.
The order is defined by
![]() ${\langle }\alpha _1,...,\alpha _n,A{\rangle }\leq {\langle }\beta _1,...,\beta _m,B{\rangle }$
iff:
${\langle }\alpha _1,...,\alpha _n,A{\rangle }\leq {\langle }\beta _1,...,\beta _m,B{\rangle }$
iff:
-
(1)
 $n\leq m$
and for every
$n\leq m$
and for every
 $i\leq n$
,
$i\leq n$
,
 $\alpha _i=\beta _i$
,
$\alpha _i=\beta _i$
, -
(2) for every
 $n<i\leq m$
,
$n<i\leq m$
,
 $\beta _i\in A$
,
$\beta _i\in A$
, -
(3)
 $B\subseteq A$
.
$B\subseteq A$
.
If
![]() $n=m$
we say that q directly extends p and denote it by
$n=m$
we say that q directly extends p and denote it by
![]() $p\leq ^* q$
.
$p\leq ^* q$
.
If U is normal then we can take
![]() $\pi =id$
and the forcing
$\pi =id$
and the forcing
![]() $\operatorname {\mathrm {Prikry}}(U)$
is the standard Prikry forcing. The requirement that the sequence is
$\operatorname {\mathrm {Prikry}}(U)$
is the standard Prikry forcing. The requirement that the sequence is
![]() $\pi $
-increasing ensures that the forcing
$\pi $
-increasing ensures that the forcing
![]() $\operatorname {\mathrm {Prikry}}(U)$
is forcing equivalent to the tree-Prikry forcing defined in [Reference Gitik, Foreman and Kanamori17]. Also, it enables to define a diagonal intersection suitable for the non-normal case, namely, for
$\operatorname {\mathrm {Prikry}}(U)$
is forcing equivalent to the tree-Prikry forcing defined in [Reference Gitik, Foreman and Kanamori17]. Also, it enables to define a diagonal intersection suitable for the non-normal case, namely, for
![]() $\{A_i\mid i<\kappa \}\subseteq U$
define
$\{A_i\mid i<\kappa \}\subseteq U$
define
This kind of diagonal intersection instead of the standard one is used to prove the Prikry property of
![]() $\operatorname {\mathrm {Prikry}}(U)$
.
$\operatorname {\mathrm {Prikry}}(U)$
.
Later we will need the easy direction of the Mathias criterion [Reference Mathias28] for Prikry-generic sequences, and the proof can be found in [Reference Benhamou3, Corollary 4.22]:
Lemma 1.3. Let
![]() $G\subseteq \operatorname {\mathrm {Prikry}}(U)$
be a generic filter producing a Prikry sequence
$G\subseteq \operatorname {\mathrm {Prikry}}(U)$
be a generic filter producing a Prikry sequence
![]() $\{c_n\mid n<\omega \}$
. Then for every
$\{c_n\mid n<\omega \}$
. Then for every
![]() $A\in U$
, there is
$A\in U$
, there is
![]() $N<\omega $
such that for every
$N<\omega $
such that for every
![]() $n\geq N$
,
$n\geq N$
,
![]() $c_n\in A$
.
$c_n\in A$
.
For more information regarding the tree-Prikry forcing see [Reference Gitik, Foreman and Kanamori17] or [Reference Benhamou3]. In the following, we define the notion of lottery sum. The terminology “lottery sum” is due to Hamkins, although the concept of the lottery sum of partial orderings has been around for quite some time and has been referred to, for example, as “disjoint sum of partial orderings”:
Definition 1.4. Let
![]() $\mathbb {P}_0,\mathbb {P}_1$
be two forcing notions. The lottery sum of
$\mathbb {P}_0,\mathbb {P}_1$
be two forcing notions. The lottery sum of
![]() $\mathbb {P}_0$
and
$\mathbb {P}_0$
and
![]() $\mathbb {P}_1$
denoted by
$\mathbb {P}_1$
denoted by
![]() $\operatorname {\mathrm {LOTT}}(\mathbb {P}_0,\mathbb {P}_1)$
is the forcing whose underlining set is
$\operatorname {\mathrm {LOTT}}(\mathbb {P}_0,\mathbb {P}_1)$
is the forcing whose underlining set is
![]() $\mathbb {P}_0\times \{0\}\cup \mathbb {P}_1\times \{1\}$
and the order is define by
$\mathbb {P}_0\times \{0\}\cup \mathbb {P}_1\times \{1\}$
and the order is define by
![]() ${\langle } p,i{\rangle }\leq {\langle } p',j{\rangle }$
iff
${\langle } p,i{\rangle }\leq {\langle } p',j{\rangle }$
iff
![]() $i=j$
and
$i=j$
and
![]() $p\leq _{\mathbb {P}_i} p'$
.
$p\leq _{\mathbb {P}_i} p'$
.
The forcing
![]() $\operatorname {\mathrm {LOTT}}(\mathbb {P}_0,\mathbb {P}_1)$
generically chooses
$\operatorname {\mathrm {LOTT}}(\mathbb {P}_0,\mathbb {P}_1)$
generically chooses
![]() $\mathbb {P}_0$
or
$\mathbb {P}_0$
or
![]() $\mathbb {P}_1$
and adds a V-generic filter for it. As Hamkins observed in [Reference Hamkins22], iterating such forcing notions leaves a certain amount of freedom when lifting ground model embeddings; this will be exploited in most of our construction.
$\mathbb {P}_1$
and adds a V-generic filter for it. As Hamkins observed in [Reference Hamkins22], iterating such forcing notions leaves a certain amount of freedom when lifting ground model embeddings; this will be exploited in most of our construction.
In Section 4 we will discuss the Extender-based Prikry forcing which was originally defined by Magidor and the second author in [Reference Gitik and Magidor21]. A more recent variation of it is due to Merimovich [Reference Merimovich29–Reference Merimovich31].
Let us present the two versions. Let E be a
![]() $(\kappa ,\lambda )$
-extender and
$(\kappa ,\lambda )$
-extender and
![]() $j=j_E:V\rightarrow M_E\simeq Ult(V,E)$
the natural elementary embedding (see [Reference Jech23] for the definition of extenders and related constructions) and suppose that
$j=j_E:V\rightarrow M_E\simeq Ult(V,E)$
the natural elementary embedding (see [Reference Jech23] for the definition of extenders and related constructions) and suppose that
![]() $f_\lambda :\kappa \rightarrow \kappa $
is a function such that
$f_\lambda :\kappa \rightarrow \kappa $
is a function such that
![]() $j(f_\lambda )(\kappa )=\lambda $
(our result uses
$j(f_\lambda )(\kappa )=\lambda $
(our result uses
![]() $\lambda =\kappa ^{++}$
and we can simply take
$\lambda =\kappa ^{++}$
and we can simply take
![]() $f_\lambda (\nu )=\nu ^{++}$
). Let us first present the Merimovich version of the Extender-based Prikry forcing.
$f_\lambda (\nu )=\nu ^{++}$
). Let us first present the Merimovich version of the Extender-based Prikry forcing.
For each set of cardinality
![]() $\leq \kappa $
,
$\leq \kappa $
,
![]() $d\in [\lambda \setminus \kappa ]^{\leq \kappa }$
with
$d\in [\lambda \setminus \kappa ]^{\leq \kappa }$
with
![]() $\kappa \in d$
. Define
$\kappa \in d$
. Define
If
![]() $A\in E(d)$
we can assume that for every
$A\in E(d)$
we can assume that for every
![]() $\nu ,\mu \in A$
,
$\nu ,\mu \in A$
,
![]() $\nu :d\rightarrow \kappa $
is order preserving,
$\nu :d\rightarrow \kappa $
is order preserving,
![]() $\kappa \in \operatorname {\mathrm {dom}}(\nu )$
,
$\kappa \in \operatorname {\mathrm {dom}}(\nu )$
,
![]() $|\nu |\leq \nu (\kappa )$
,
$|\nu |\leq \nu (\kappa )$
,
![]() $\nu (\kappa )=\mu (\kappa )\rightarrow \operatorname {\mathrm {dom}}(\nu )=\operatorname {\mathrm {dom}}(\mu )$
. Merimovich calls such a set a good set.
$\nu (\kappa )=\mu (\kappa )\rightarrow \operatorname {\mathrm {dom}}(\nu )=\operatorname {\mathrm {dom}}(\mu )$
. Merimovich calls such a set a good set.
Definition 1.5. The conditions of
![]() $\mathbb {P}_E$
are pairs
$\mathbb {P}_E$
are pairs
![]() $p={\langle } f^p,A^p{\rangle }$
such that:
$p={\langle } f^p,A^p{\rangle }$
such that:
-
(1)
 $f^p:d\rightarrow [\kappa ]^{<\omega }$
is the “Cohen Part” of the condition,
$f^p:d\rightarrow [\kappa ]^{<\omega }$
is the “Cohen Part” of the condition,
 $d\in [\lambda \setminus \kappa ]^{<\omega }$
,
$d\in [\lambda \setminus \kappa ]^{<\omega }$
,
 $\kappa \in d$
.
$\kappa \in d$
. -
(2)
 $A^p\in E(d)$
is a good set.
$A^p\in E(d)$
is a good set. -
(3) For every
 $\nu \in A^p$
and
$\nu \in A^p$
and
 $\alpha \in \operatorname {\mathrm {dom}}(\nu )$
,
$\alpha \in \operatorname {\mathrm {dom}}(\nu )$
,
 $\max (f^p(\alpha ))<\nu (\kappa )$
.
$\max (f^p(\alpha ))<\nu (\kappa )$
.
The order of
![]() $\mathbb {P}_E$
is defined in two steps: a direct extension is defined by
$\mathbb {P}_E$
is defined in two steps: a direct extension is defined by
![]() ${\langle } f,A{\rangle }\leq ^* {\langle } g,B{\rangle }$
if:
${\langle } f,A{\rangle }\leq ^* {\langle } g,B{\rangle }$
if:
-
(1)
 $f\subseteq g$
.
$f\subseteq g$
. -
(2)
 $B\restriction \operatorname {\mathrm {dom}}(f):=\{\nu \restriction \operatorname {\mathrm {dom}}(\nu )\cap \operatorname {\mathrm {dom}}(f)\mid \nu \in B\}\subseteq A$
.
$B\restriction \operatorname {\mathrm {dom}}(f):=\{\nu \restriction \operatorname {\mathrm {dom}}(\nu )\cap \operatorname {\mathrm {dom}}(f)\mid \nu \in B\}\subseteq A$
.
A one-point extension of
![]() $p={\langle } f,A{\rangle }$
for
$p={\langle } f,A{\rangle }$
for
![]() $\nu \in A$
is defined by
$\nu \in A$
is defined by
![]() $p^{\smallfrown }\nu ={\langle } g,B{\rangle }$
where:
$p^{\smallfrown }\nu ={\langle } g,B{\rangle }$
where:
-
(1)
 $\operatorname {\mathrm {dom}}(g)=\operatorname {\mathrm {dom}}(f)$
.
$\operatorname {\mathrm {dom}}(g)=\operatorname {\mathrm {dom}}(f)$
. -
(2) For every
 $\alpha \in \operatorname {\mathrm {dom}}(g),$
$\alpha \in \operatorname {\mathrm {dom}}(g),$
 $$ \begin{align*}g(\alpha)=\begin{cases} f(\alpha)^{\smallfrown}\nu(\alpha), & \alpha\in\operatorname{\mathrm{dom}}(\nu),\\ f(\alpha), & \text{else}.\end{cases}\end{align*} $$
$$ \begin{align*}g(\alpha)=\begin{cases} f(\alpha)^{\smallfrown}\nu(\alpha), & \alpha\in\operatorname{\mathrm{dom}}(\nu),\\ f(\alpha), & \text{else}.\end{cases}\end{align*} $$
-
(3)
 $B=\{\mu \in A\mid \sup _{\alpha \in \operatorname {\mathrm {dom}}(\nu )}(\nu (\alpha )+1)\leq \mu (\kappa )\}$
.
$B=\{\mu \in A\mid \sup _{\alpha \in \operatorname {\mathrm {dom}}(\nu )}(\nu (\alpha )+1)\leq \mu (\kappa )\}$
.
An n-point extension
![]() $p{}^{\smallfrown }\vec {\nu }$
is defined recursively by consecutive one-point extensions. A general extension is defined by
$p{}^{\smallfrown }\vec {\nu }$
is defined recursively by consecutive one-point extensions. A general extension is defined by
![]() $p\leq q$
iff for some
$p\leq q$
iff for some
![]() $\vec {\nu }\in [A^p]^{<\omega }$
,
$\vec {\nu }\in [A^p]^{<\omega }$
,
![]() $p^{\smallfrown }\vec {\nu }\leq ^* q$
.
$p^{\smallfrown }\vec {\nu }\leq ^* q$
.
As in [Reference Merimovich30], we will sometime replace the large set A in a condition
![]() ${\langle } f,A{\rangle }$
with a Tree T which is
${\langle } f,A{\rangle }$
with a Tree T which is
![]() $E(\operatorname {\mathrm {dom}}(f))$
-fat.
$E(\operatorname {\mathrm {dom}}(f))$
-fat.
Let us now present the original version defined by Magidor and the second author from [Reference Gitik and Magidor21]. Define for every
![]() $\kappa \leq \alpha <\lambda $
:
$\kappa \leq \alpha <\lambda $
:
These are P-point ultrafilters. For every
![]() $\alpha \leq \beta <\lambda $
we define that
$\alpha \leq \beta <\lambda $
we define that
![]() $\alpha \leq _E\beta $
if there is some
$\alpha \leq _E\beta $
if there is some
![]() $f:\kappa \rightarrow \kappa $
,
$f:\kappa \rightarrow \kappa $
,
![]() $j(f)(\beta )=\alpha $
. This implies that f Rudin–Keisler projects
$j(f)(\beta )=\alpha $
. This implies that f Rudin–Keisler projects
![]() $U_\beta $
onto
$U_\beta $
onto
![]() $U_\alpha $
. For every such pair
$U_\alpha $
. For every such pair
![]() $\alpha \leq _E\beta $
fix such a projection
$\alpha \leq _E\beta $
fix such a projection
![]() $\pi _{\beta ,\alpha }$
such that
$\pi _{\beta ,\alpha }$
such that
![]() $\pi _{\alpha ,\alpha }=id$
. The projections to the normal measure
$\pi _{\alpha ,\alpha }=id$
. The projections to the normal measure
![]() $U_\kappa $
have a uniform definition,
$U_\kappa $
have a uniform definition,
![]() $\pi _{\alpha ,\kappa }(\nu )=\nu ^0$
where
$\pi _{\alpha ,\kappa }(\nu )=\nu ^0$
where
![]() $\nu ^0$
is the maximal inaccessible
$\nu ^0$
is the maximal inaccessible
![]() $\nu ^*\leq \nu $
such that
$\nu ^*\leq \nu $
such that
![]() $f_\lambda \restriction \nu ^*:\nu ^*\rightarrow \nu ^*$
,
$f_\lambda \restriction \nu ^*:\nu ^*\rightarrow \nu ^*$
,
![]() $f_\lambda (\nu ^*)>\nu $
, and
$f_\lambda (\nu ^*)>\nu $
, and
![]() $\pi _{\alpha ,\kappa }(\nu )=0$
if there is no such
$\pi _{\alpha ,\kappa }(\nu )=0$
if there is no such
![]() $\nu ^*$
. Suppose that the system
$\nu ^*$
. Suppose that the system
![]() ${\langle } U_\alpha ,\pi _{\alpha ,\beta }\mid \alpha \leq \beta <\lambda , \alpha \leq _E\beta {\rangle }$
is a nice system (see [Reference Gitik and Magidor21] or [Reference Gitik, Foreman and Kanamori17, Discussion after Lemma 3.5]). Let us say that
${\langle } U_\alpha ,\pi _{\alpha ,\beta }\mid \alpha \leq \beta <\lambda , \alpha \leq _E\beta {\rangle }$
is a nice system (see [Reference Gitik and Magidor21] or [Reference Gitik, Foreman and Kanamori17, Discussion after Lemma 3.5]). Let us say that
![]() $\nu $
is permitted for
$\nu $
is permitted for
![]() $\nu _0,...,\nu _n$
is
$\nu _0,...,\nu _n$
is
![]() $\nu ^0>\max _{i=0,...,n}\nu ^0_i$
.
$\nu ^0>\max _{i=0,...,n}\nu ^0_i$
.
Definition 1.6.
The conditions of the forcing
![]() $\mathcal {P}_E$
are pairs
$\mathcal {P}_E$
are pairs
![]() $p={\langle } f,T{\rangle }$
such that:
$p={\langle } f,T{\rangle }$
such that:
-
(1)
 $f:\lambda \setminus \kappa \rightarrow [\kappa ]^{<\omega }$
,
$f:\lambda \setminus \kappa \rightarrow [\kappa ]^{<\omega }$
,
 $\kappa \in \operatorname {\mathrm {dom}}(f)$
,
$\kappa \in \operatorname {\mathrm {dom}}(f)$
,
 $|f|\leq \kappa $
.
$|f|\leq \kappa $
. -
(2) For each
 $\alpha \in \operatorname {\mathrm {Supp}}(p):=\operatorname {\mathrm {dom}}(f)$
,
$\alpha \in \operatorname {\mathrm {Supp}}(p):=\operatorname {\mathrm {dom}}(f)$
,
 $\pi _{\alpha ,\kappa }^{\prime \prime }f(\alpha )$
is a finite increasing sequence.
$\pi _{\alpha ,\kappa }^{\prime \prime }f(\alpha )$
is a finite increasing sequence. -
(3) The domain of f has a
 $\leq _E$
-maximal element
$\leq _E$
-maximal element
 $mc(p):=\alpha =\max (\operatorname {\mathrm {Supp}}(p))$
.
$mc(p):=\alpha =\max (\operatorname {\mathrm {Supp}}(p))$
. -
(4)
 $\pi _{mc(p),\kappa }"f(mc(p))=f(\kappa )$
.
$\pi _{mc(p),\kappa }"f(mc(p))=f(\kappa )$
. -
(5) For every
 $\gamma \in \operatorname {\mathrm {Supp}}(p)$
,
$\gamma \in \operatorname {\mathrm {Supp}}(p)$
,
 $\pi _{mc(p),\gamma }(\max (f(mc(p)))$
is not permitted to
$\pi _{mc(p),\gamma }(\max (f(mc(p)))$
is not permitted to
 $f(\gamma )$
.
$f(\gamma )$
. -
(6) T is a
 $U_{mc(p)}$
-splitting tree with stem
$U_{mc(p)}$
-splitting tree with stem
 $f(mc(p))$
, namely, for
$f(mc(p))$
, namely, for
 $s\in T$
, either
$s\in T$
, either
 $s\leq t$
, or
$s\leq t$
, or
 $s\geq t$
and
$s\geq t$
and
 $\operatorname {\mathrm {Succ}}_T(s):=\{\alpha <\kappa \mid s{}^{\smallfrown }\alpha \in T\}\in U_{mc(p)}$
.
$\operatorname {\mathrm {Succ}}_T(s):=\{\alpha <\kappa \mid s{}^{\smallfrown }\alpha \in T\}\in U_{mc(p)}$
. -
(7) For every
 $\nu \in \operatorname {\mathrm {Succ}}_T(f(mc(p)))$
,
$\nu \in \operatorname {\mathrm {Succ}}_T(f(mc(p)))$
,  $$ \begin{align*}|\{\gamma\in \operatorname{\mathrm{Supp}}(p)\mid \nu\text{ is permitted to } f(\gamma)\}|\leq \nu^0.\end{align*} $$
$$ \begin{align*}|\{\gamma\in \operatorname{\mathrm{Supp}}(p)\mid \nu\text{ is permitted to } f(\gamma)\}|\leq \nu^0.\end{align*} $$
The order is defined
![]() $p\leq q$
if:
$p\leq q$
if:
-
(1)
 $\operatorname {\mathrm {Supp}}(p)\subseteq \operatorname {\mathrm {Supp}}(q)$
.
$\operatorname {\mathrm {Supp}}(p)\subseteq \operatorname {\mathrm {Supp}}(q)$
. -
(2) For
 $\gamma \in \operatorname {\mathrm {Supp}}(p)$
,
$\gamma \in \operatorname {\mathrm {Supp}}(p)$
,
 $f^q(\gamma )$
is an end-extension of
$f^q(\gamma )$
is an end-extension of
 $f^p(\gamma )$
.
$f^p(\gamma )$
. -
(3)
 $f^q(mc(p))\in T^p$
.
$f^q(mc(p))\in T^p$
. -
(4) For
 $\gamma\hspace{-0.5pt} \in\hspace{-0.5pt} \operatorname {\mathrm {Supp}}(p)$
,
$\gamma\hspace{-0.5pt} \in\hspace{-0.5pt} \operatorname {\mathrm {Supp}}(p)$
,
 $f^q(\gamma )\setminus f^p(\gamma )\hspace{-0.5pt}=\hspace{-0.5pt}\pi _{mc(p),\gamma }^{\prime \prime }f^q(mc(p))\hspace{-0.5pt}\setminus\hspace{-0.5pt} f^p(mc(p))\restriction (i+1)$
, where i is maximal such that
$f^q(\gamma )\setminus f^p(\gamma )\hspace{-0.5pt}=\hspace{-0.5pt}\pi _{mc(p),\gamma }^{\prime \prime }f^q(mc(p))\hspace{-0.5pt}\setminus\hspace{-0.5pt} f^p(mc(p))\restriction (i+1)$
, where i is maximal such that
 $f^q(mc(p))$
is not permitted for
$f^q(mc(p))$
is not permitted for
 $f^p(\gamma )$
.
$f^p(\gamma )$
. -
(5)
 $\pi _{mc(q),mc(p)}^{\prime \prime }T^q\subseteq T^p$
.
$\pi _{mc(q),mc(p)}^{\prime \prime }T^q\subseteq T^p$
. -
(6) For every
 $\gamma \in \operatorname {\mathrm {Supp}}(p)$
, and
$\gamma \in \operatorname {\mathrm {Supp}}(p)$
, and
 $\nu \in \operatorname {\mathrm {Succ}}_{T^q}(f^q(mc(q)))$
, such that
$\nu \in \operatorname {\mathrm {Succ}}_{T^q}(f^q(mc(q)))$
, such that
 $\nu $
is permitted for
$\nu $
is permitted for
 $f^q(\gamma )$
(so by condition (7) there are only
$f^q(\gamma )$
(so by condition (7) there are only
 $\nu ^0$
-many such
$\nu ^0$
-many such
 $\gamma $
’s) then
$\gamma $
’s) then
 $\pi _{mc(q),\gamma }(\nu )=\pi _{mc(p),\gamma }(\pi _{mc(q),mc(p)}(\nu )).$
$\pi _{mc(q),\gamma }(\nu )=\pi _{mc(p),\gamma }(\pi _{mc(q),mc(p)}(\nu )).$
1.2 Canonical functions
The main construction of this paper uses the notion of canonical functions:
Definition 1.7. For every limit ordinal
![]() $\delta <\kappa ^+$
, fix a cofinal sequence
$\delta <\kappa ^+$
, fix a cofinal sequence
![]() $\bar {\delta }=\{ \delta _i\mid i<cf(\delta )\}$
. Let us define inductively functions
$\bar {\delta }=\{ \delta _i\mid i<cf(\delta )\}$
. Let us define inductively functions
![]() $\tau _\alpha :\kappa \rightarrow \kappa $
for
$\tau _\alpha :\kappa \rightarrow \kappa $
for
![]() $\alpha <\kappa ^+$
:
$\alpha <\kappa ^+$
:
Proposition 1.8. Let
![]() $\lambda \leq \kappa $
be a regular cardinal. Then:
$\lambda \leq \kappa $
be a regular cardinal. Then:
-
(1) For every
 $\alpha <\beta <\lambda ^+$
,
$\alpha <\beta <\lambda ^+$
,
 $\{\nu \mid \tau _{\alpha }(\nu )\geq \tau _{\beta }(\nu )\}$
is bounded in
$\{\nu \mid \tau _{\alpha }(\nu )\geq \tau _{\beta }(\nu )\}$
is bounded in
 $\lambda $
.
$\lambda $
. -
(2) For every any
 $\alpha <\lambda ^+$
,
$\alpha <\lambda ^+$
,
 $\tau _{\alpha }:\lambda \rightarrow \lambda $
.
$\tau _{\alpha }:\lambda \rightarrow \lambda $
. -
(3) For every normal measure
 $\mathcal {V}$
on
$\mathcal {V}$
on
 $\lambda $
, and for every
$\lambda $
, and for every
 $\alpha <\lambda ^+$
,
$\alpha <\lambda ^+$
,
 $[\tau _{\alpha }]_{\mathcal {V}}=\alpha $
.
$[\tau _{\alpha }]_{\mathcal {V}}=\alpha $
. -
(4) If
 $\lambda <\kappa $
, then for every
$\lambda <\kappa $
, then for every
 $\beta $
,
$\beta $
,
 $\tau _{\beta }(\lambda )<\lambda ^+$
.
$\tau _{\beta }(\lambda )<\lambda ^+$
.
Proof For
![]() $(1)$
, we prove inductively on
$(1)$
, we prove inductively on
![]() $\beta <\lambda ^+$
that for every
$\beta <\lambda ^+$
that for every
![]() $\alpha <\beta $
,
$\alpha <\beta $
,
![]() $(1)$
holds. For
$(1)$
holds. For
![]() $\beta =0$
this is vacuous. The successor stage is also easy since for every x,
$\beta =0$
this is vacuous. The successor stage is also easy since for every x,
![]() $\tau _{\beta }(x)<\tau _{\beta +1}(x)$
so if
$\tau _{\beta }(x)<\tau _{\beta +1}(x)$
so if
![]() $\alpha <\beta $
then by induction hypothesis there is
$\alpha <\beta $
then by induction hypothesis there is
![]() $\xi <\lambda $
from which
$\xi <\lambda $
from which
![]() $\tau _{\beta }$
dominates
$\tau _{\beta }$
dominates
![]() $\tau _{\alpha }$
, i.e.,
$\tau _{\alpha }$
, i.e.,
![]() $\forall \nu \in (\xi ,\lambda ).\tau _\alpha (\nu )<\tau _{\beta }(\nu )$
. It follows that for the same
$\forall \nu \in (\xi ,\lambda ).\tau _\alpha (\nu )<\tau _{\beta }(\nu )$
. It follows that for the same
![]() $\xi $
,
$\xi $
,
![]() $\tau _{\alpha }(\nu )<\tau _{\beta +1}(\nu )$
. As for limit points
$\tau _{\alpha }(\nu )<\tau _{\beta +1}(\nu )$
. As for limit points
![]() $\delta $
. Fix any
$\delta $
. Fix any
![]() $\alpha <\delta $
, then there is
$\alpha <\delta $
, then there is
![]() $i< cf(\delta )\leq \lambda $
such that
$i< cf(\delta )\leq \lambda $
such that
![]() $\delta _i>\alpha $
. By induction hypothesis there is
$\delta _i>\alpha $
. By induction hypothesis there is
![]() $\xi _i<\lambda $
such that
$\xi _i<\lambda $
such that
![]() $\tau _{\delta _i}(\nu )>\tau _{\alpha }(\nu )$
for every
$\tau _{\delta _i}(\nu )>\tau _{\alpha }(\nu )$
for every
![]() $\nu \in (\xi _i,\lambda )$
. Let
$\nu \in (\xi _i,\lambda )$
. Let
![]() $\xi ^*:=\max \{\xi _i, i\}+1<\lambda $
. It follows that for every
$\xi ^*:=\max \{\xi _i, i\}+1<\lambda $
. It follows that for every
![]() $\nu \in (\xi ^*,\lambda )$
,
$\nu \in (\xi ^*,\lambda )$
,
![]() $\nu>i$
, and hence
$\nu>i$
, and hence
Prove
![]() $(2)$
–
$(2)$
–
![]() $(4)$
by induction on
$(4)$
by induction on
![]() $\alpha <\lambda ^+$
. For
$\alpha <\lambda ^+$
. For
![]() $\alpha =0$
this is trivial. Suppose that
$\alpha =0$
this is trivial. Suppose that
![]() $(2)$
–
$(2)$
–
![]() $(4)$
hold for
$(4)$
hold for
![]() $\alpha $
then clearly by induction hypothesis
$\alpha $
then clearly by induction hypothesis
![]() $\tau _{\alpha +1}:\lambda \rightarrow \lambda $
, and
$\tau _{\alpha +1}:\lambda \rightarrow \lambda $
, and
![]() $\tau _{\alpha +1}(\lambda )=\tau _{\alpha }(\lambda )+1<\lambda ^+$
, namely
$\tau _{\alpha +1}(\lambda )=\tau _{\alpha }(\lambda )+1<\lambda ^+$
, namely
![]() $(2)$
and
$(2)$
and
![]() $(4)$
follow. Also,
$(4)$
follow. Also,
![]() $\lambda =\{\nu <\lambda \mid \tau _{\alpha }(\nu )+1=\tau _{\alpha +1}(\nu )\}\in \mathcal {V}$
, ane hence by the Lós theorem and the induction hypothesis:
$\lambda =\{\nu <\lambda \mid \tau _{\alpha }(\nu )+1=\tau _{\alpha +1}(\nu )\}\in \mathcal {V}$
, ane hence by the Lós theorem and the induction hypothesis:
Suppose that
![]() $\delta <\lambda ^+$
is limit, then by induction hypothesis, for every
$\delta <\lambda ^+$
is limit, then by induction hypothesis, for every
![]() $x<\lambda $
and
$x<\lambda $
and
![]() $y<\min (x,cf(\delta ))<\lambda $
,
$y<\min (x,cf(\delta ))<\lambda $
,
![]() $\tau _{\delta _y}(x)<\lambda $
. It follows from the regularity of
$\tau _{\delta _y}(x)<\lambda $
. It follows from the regularity of
![]() $\lambda $
that
$\lambda $
that
This concludes
![]() $(2)$
. Also,
$(2)$
. Also,
![]() $(4)$
follows similarly using the regularity of
$(4)$
follows similarly using the regularity of
![]() $\lambda ^+$
. As for
$\lambda ^+$
. As for
![]() $(3)$
, we use
$(3)$
, we use
![]() $(1)$
to conclude that for every
$(1)$
to conclude that for every
![]() $\alpha <\delta $
,
$\alpha <\delta $
,
![]() $\{\nu <\lambda \mid \tau _{\alpha }(\nu )\geq \tau _{\delta }(\nu )\}$
is bounded. Hence by induction
$\{\nu <\lambda \mid \tau _{\alpha }(\nu )\geq \tau _{\delta }(\nu )\}$
is bounded. Hence by induction
![]() $\alpha =[\tau _{\alpha }]_{\mathcal {V}}<[\tau _{\delta }]_{\mathcal {V}}$
. It follows that
$\alpha =[\tau _{\alpha }]_{\mathcal {V}}<[\tau _{\delta }]_{\mathcal {V}}$
. It follows that
![]() $\delta \leq [\tau _{\delta }]_{\mathcal {V}}$
. For the other direction, suppose that
$\delta \leq [\tau _{\delta }]_{\mathcal {V}}$
. For the other direction, suppose that
![]() $[f]_{\mathcal {V}}<[\tau _{\delta }]_{\mathcal {V}}$
, then
$[f]_{\mathcal {V}}<[\tau _{\delta }]_{\mathcal {V}}$
, then
By definition of
![]() $\tau _{\delta }$
, for every
$\tau _{\delta }$
, for every
![]() $x\in E$
, there is
$x\in E$
, there is
![]() $y_x<\min (x,cf(\delta ))$
such that
$y_x<\min (x,cf(\delta ))$
such that
![]() $\tau _{\delta _{t_x}}(x)>f(x)$
. The function
$\tau _{\delta _{t_x}}(x)>f(x)$
. The function
![]() $x\mapsto y_x$
is regressive, and by normality we conclude that there is
$x\mapsto y_x$
is regressive, and by normality we conclude that there is
![]() $y^*<cf(\delta )$
and
$y^*<cf(\delta )$
and
![]() $E'\subseteq E$
such that for every
$E'\subseteq E$
such that for every
![]() $x\in E'$
,
$x\in E'$
,
![]() $f(x)<\tau _{\delta _{y^*}}(x)$
. Hence
$f(x)<\tau _{\delta _{y^*}}(x)$
. Hence
![]() $[f]_{\mathcal {V}}<[\tau _{\delta _{y^*}}]_{\mathcal {V}}=\delta _{y^*}<\delta $
and in turn
$[f]_{\mathcal {V}}<[\tau _{\delta _{y^*}}]_{\mathcal {V}}=\delta _{y^*}<\delta $
and in turn
![]() $\delta =[\tau _{\delta }]_{\mathcal {V}}$
.
$\delta =[\tau _{\delta }]_{\mathcal {V}}$
.
2 The results where GCH holds
2.1 Non-Galvin ultrafilter from optimal assumption
In [Reference Benhamou, Garti and Shelah5], Garti, Shelah, and the first author constructed a model with a
![]() $\kappa $
-complete ultrafilter which contains
$\kappa $
-complete ultrafilter which contains
![]() $Cub_\kappa $
and fails to satisfy the Galvin property. The initial assumption was a supercompact cardinal and the construction went through adding slim Kurepa trees.
$Cub_\kappa $
and fails to satisfy the Galvin property. The initial assumption was a supercompact cardinal and the construction went through adding slim Kurepa trees.
Here we present a different construction. Our initial assumption will be a measurable cardinal and the property obtained will be a certain strengthening of the negation of the Galvin property. It will be used further to produce many Cohens.
Let us first present the stronger form of negation:
Definition 2.1. Let U be a
![]() $\kappa $
-complete ultrafilter non-normal over
$\kappa $
-complete ultrafilter non-normal over
![]() $\kappa $
. We call a family
$\kappa $
. We call a family
![]() $\{ A_\alpha \mid \alpha <\kappa ^+\}\subseteq U$
a strong witness for the failure of the Galvin property iff for every subfamily
$\{ A_\alpha \mid \alpha <\kappa ^+\}\subseteq U$
a strong witness for the failure of the Galvin property iff for every subfamily
![]() ${\langle } A_{\alpha _\xi } \mid \xi <\kappa {\rangle }$
of size
${\langle } A_{\alpha _\xi } \mid \xi <\kappa {\rangle }$
of size
![]() $\kappa $
the following holds:
$\kappa $
the following holds:
Remark 2.2.
-
(1) Note that the interval
 $[\kappa , [id]_U)$
is non-empty since U is not normal.
$[\kappa , [id]_U)$
is non-empty since U is not normal. -
(2) The family
 $\{ A_\alpha \mid \alpha <\kappa ^+\}$
witnesses the failure of the Galvin property for U.
$\{ A_\alpha \mid \alpha <\kappa ^+\}$
witnesses the failure of the Galvin property for U.
Proof Since whenever
![]() ${\langle } A_{\alpha _\xi } \mid \xi <\kappa {\rangle }$
is a subfamily of size
${\langle } A_{\alpha _\xi } \mid \xi <\kappa {\rangle }$
is a subfamily of size
![]() $\kappa $
, then
$\kappa $
, then
![]() $\bigcap _{\xi <\kappa } A_{\alpha _\xi }$
is not in U. Otherwise, suppose that
$\bigcap _{\xi <\kappa } A_{\alpha _\xi }$
is not in U. Otherwise, suppose that
![]() $\bigcap _{\xi <\kappa } A_{\alpha _\xi }=B \in U$
. Then
$\bigcap _{\xi <\kappa } A_{\alpha _\xi }=B \in U$
. Then
![]() $[id]_U \in j_U(B)$
, but
$[id]_U \in j_U(B)$
, but
![]() $j_U(B)=\bigcap _{\zeta <j_U(\kappa )}A^{\prime }_{\alpha _\zeta }$
. However,
$j_U(B)=\bigcap _{\zeta <j_U(\kappa )}A^{\prime }_{\alpha _\zeta }$
. However,
![]() $[id]_U \not \in A^{\prime }_{\alpha _\zeta }$
, for every
$[id]_U \not \in A^{\prime }_{\alpha _\zeta }$
, for every
![]() $\zeta , \kappa \leq \zeta < [id]_U$
. Contradiction.
$\zeta , \kappa \leq \zeta < [id]_U$
. Contradiction.
Lemma 2.3. Suppose that
![]() $\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness for the failure of the Galvin property of the ultrafilter U over
$\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness for the failure of the Galvin property of the ultrafilter U over
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $U^0=\{X\subseteq \kappa \mid \kappa \in j_U(X)\}$
be a projection of U to a normal ultrafilter,
$U^0=\{X\subseteq \kappa \mid \kappa \in j_U(X)\}$
be a projection of U to a normal ultrafilter,
![]() $\nu \mapsto \pi _{nor}(\nu )$
a projection map, and
$\nu \mapsto \pi _{nor}(\nu )$
a projection map, and
![]() $k: M_{U^0}\to M_U$
the corresponding elementary embedding. Assume that
$k: M_{U^0}\to M_U$
the corresponding elementary embedding. Assume that
![]() $crit(k)=j_{U^0}(\kappa )=[id]_U$
. Then
$crit(k)=j_{U^0}(\kappa )=[id]_U$
. Then
![]() $[id]_U \not \in B$
, for every
$[id]_U \not \in B$
, for every
![]() $B \in j_U(\{ A_\alpha \mid \alpha <\kappa ^+\})$
which is in
$B \in j_U(\{ A_\alpha \mid \alpha <\kappa ^+\})$
which is in
![]() $\operatorname {\mathrm {rng}}(k)\setminus \operatorname {\mathrm {rng}}(j_U)$
.
$\operatorname {\mathrm {rng}}(k)\setminus \operatorname {\mathrm {rng}}(j_U)$
.
Proof Let B be as in the statement of the lemma. Pick
![]() $A'\subseteq j_{U^0}(\kappa )$
such that
$A'\subseteq j_{U^0}(\kappa )$
such that
![]() $k(A')=B$
. Then
$k(A')=B$
. Then
![]() $A' \not \in \operatorname {\mathrm {rng}}(j_{U^0})$
, since otherwise its image B will be in the range of
$A' \not \in \operatorname {\mathrm {rng}}(j_{U^0})$
, since otherwise its image B will be in the range of
![]() $j_U=k\circ j_{U^0}$
. Denote by
$j_U=k\circ j_{U^0}$
. Denote by
Since
![]() $U^0$
is normal, there is
$U^0$
is normal, there is
![]() $f:\kappa \rightarrow \kappa ^+$
such that
$f:\kappa \rightarrow \kappa ^+$
such that
![]() $A'=A^{\prime }_{j_{U^0}(f)(\kappa )}$
and thus
$A'=A^{\prime }_{j_{U^0}(f)(\kappa )}$
and thus
Since B is not in the range of k, f is not constant. Recall that
![]() $\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness for U being non-Galvin ultrafilter over
$\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness for U being non-Galvin ultrafilter over
![]() $\kappa $
. Apply this to the family
$\kappa $
. Apply this to the family
![]() $\{ A_{f(\nu )} \mid \nu <\kappa \}.$
It follows that
$\{ A_{f(\nu )} \mid \nu <\kappa \}.$
It follows that
![]() $[id]_U\not \in A^{\prime \prime }_{j_{U}(f)(\kappa )}=B.$
$[id]_U\not \in A^{\prime \prime }_{j_{U}(f)(\kappa )}=B.$
Before proving the main result of this section we present two preservation theorems for being a strong witnesses for the failure of the Galvin property. These theorems are not used later and the reader can proceed directly to Theorem 2.6.
Theorem 2.4. Assume
![]() $2^{\kappa }=\kappa ^+$
. Suppose that the family
$2^{\kappa }=\kappa ^+$
. Suppose that the family
![]() $\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness for U being a non-Galvin ultrafilter over
$\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness for U being a non-Galvin ultrafilter over
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $U^0=\{X\subseteq \kappa \mid \kappa \in j_U(X)\}$
be a projection of U to a normal ultrafilter,
$U^0=\{X\subseteq \kappa \mid \kappa \in j_U(X)\}$
be a projection of U to a normal ultrafilter,
![]() $\nu \mapsto \pi _{nor}(\nu )$
a projection map, and
$\nu \mapsto \pi _{nor}(\nu )$
a projection map, and
![]() $k: M_{U^0}\to M_U$
the corresponding elementary embedding. Assume that
$k: M_{U^0}\to M_U$
the corresponding elementary embedding. Assume that
![]() $crit(k)=j_{U^0}(\kappa )$
and
$crit(k)=j_{U^0}(\kappa )$
and
![]() $[id]_U=j_{U^0}(\kappa )$
.
$[id]_U=j_{U^0}(\kappa )$
.
Suppose that
![]() $V^*$
is an extension of V in which all the embeddings
$V^*$
is an extension of V in which all the embeddings
![]() $j_{U^0},j_U, k$
extend to an elementary embedding
$j_{U^0},j_U, k$
extend to an elementary embedding
![]() $j^{0*}:V^*\to M^{0*},j^*:V^*\to M^*$
,
$j^{0*}:V^*\to M^{0*},j^*:V^*\to M^*$
,
![]() $k^*:M^{0*}\to M^*$
. Define
$k^*:M^{0*}\to M^*$
. Define
![]() $U^*=\{X \subseteq \kappa \mid [id]_U \in j^*(X)\}$
.
$U^*=\{X \subseteq \kappa \mid [id]_U \in j^*(X)\}$
.
Then
![]() $\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness that
$\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness that
![]() $U^*$
is a non-Galvin ultrafilter over
$U^*$
is a non-Galvin ultrafilter over
![]() $\kappa $
.
$\kappa $
.
Proof Note that
![]() $(\kappa ^+)^{V^*}=(\kappa ^+)^V$
. Just otherwise,
$(\kappa ^+)^{V^*}=(\kappa ^+)^V$
. Just otherwise,
![]() $(\kappa ^{++})^V $
will be
$(\kappa ^{++})^V $
will be
![]() $\leq (\kappa ^+)^{V^*}$
, and then,
$\leq (\kappa ^+)^{V^*}$
, and then,
![]() $j^*(\kappa )>(\kappa ^{++})^V$
. This is impossible, since
$j^*(\kappa )>(\kappa ^{++})^V$
. This is impossible, since
![]() $j^*$
extends
$j^*$
extends
![]() $j_U$
. The rest follows from the previous lemma and the fact that
$j_U$
. The rest follows from the previous lemma and the fact that
![]() $[\kappa , [id]_U)\subseteq \operatorname {\mathrm {rng}}(k)\setminus \operatorname {\mathrm {rng}}(j_{U})$
since
$[\kappa , [id]_U)\subseteq \operatorname {\mathrm {rng}}(k)\setminus \operatorname {\mathrm {rng}}(j_{U})$
since
![]() $crit(k)=j_{U^0}(\kappa )=[id]_U$
.
$crit(k)=j_{U^0}(\kappa )=[id]_U$
.
Theorem 2.5. Assume
![]() $2^{\kappa }=\kappa ^+$
. Suppose that
$2^{\kappa }=\kappa ^+$
. Suppose that
![]() $\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness for U being a non-Galvin ultrafilter over
$\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness for U being a non-Galvin ultrafilter over
![]() $\kappa $
which contains
$\kappa $
which contains
![]() $Cub_\kappa $
and be a witnessing family.
$Cub_\kappa $
and be a witnessing family.
Let
![]() $V^*$
be a
$V^*$
be a
![]() $\kappa $
-c.c. extension of V in which
$\kappa $
-c.c. extension of V in which
![]() $j_U$
extends to an elementary embedding
$j_U$
extends to an elementary embedding
![]() $j^*:V^*\to M^*$
, where
$j^*:V^*\to M^*$
, where
![]() $M^*$
is a corresponding extension of
$M^*$
is a corresponding extension of
![]() $M_U$
.
$M_U$
.
Define
![]() $U^*=\{X \subseteq \kappa \mid [id]_U \in j^*(X)\}$
.
$U^*=\{X \subseteq \kappa \mid [id]_U \in j^*(X)\}$
.
Then
![]() $\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness that
$\{ A_\alpha \mid \alpha <\kappa ^+\}$
is a strong witness that
![]() $U^*$
is a non-Galvin ultrafilter over
$U^*$
is a non-Galvin ultrafilter over
![]() $\kappa $
.
$\kappa $
.
Proof Suppose now that
![]() ${\langle } A_{\alpha _\xi } \mid \xi <\kappa {\rangle }$
is a subfamily of
${\langle } A_{\alpha _\xi } \mid \xi <\kappa {\rangle }$
is a subfamily of
![]() $\{ A_\alpha \mid \alpha <\kappa ^+\}$
of size
$\{ A_\alpha \mid \alpha <\kappa ^+\}$
of size
![]() $\kappa $
in
$\kappa $
in
![]() ${V^*}$
.
${V^*}$
.
Work in V. Let
![]() be a name of
be a name of
![]() $\alpha _\xi $
. By
$\alpha _\xi $
. By
![]() $\kappa $
-c.c., then for every
$\kappa $
-c.c., then for every
![]() $\xi <\kappa $
there will be
$\xi <\kappa $
there will be
![]() $s_\xi \subseteq \kappa ^+$
of cardinality less than
$s_\xi \subseteq \kappa ^+$
of cardinality less than
![]() $\kappa $
, such that
$\kappa $
, such that
![]() .
.
Let
![]() $S=\sup _{\xi <\kappa }s_\xi $
. Enumerate
$S=\sup _{\xi <\kappa }s_\xi $
. Enumerate
![]() $S={\langle } \beta _i\mid i<\kappa {\rangle }$
such that we if
$S={\langle } \beta _i\mid i<\kappa {\rangle }$
such that we if
![]() $\beta _i\in s_\zeta $
and
$\beta _i\in s_\zeta $
and
![]() $\beta _j\in s_\mu $
where
$\beta _j\in s_\mu $
where
![]() $\zeta <\mu $
then
$\zeta <\mu $
then
![]() $i<j$
, i.e., enumerate first
$i<j$
, i.e., enumerate first
![]() $s_0$
then
$s_0$
then
![]() $s_1$
and so on, such that the resulting enumeration of S is of order-type
$s_1$
and so on, such that the resulting enumeration of S is of order-type
![]() $\kappa $
. This is possible since each
$\kappa $
. This is possible since each
![]() $s_\zeta $
has cardinality less than
$s_\zeta $
has cardinality less than
![]() $\kappa $
. Define
$\kappa $
. Define
Clearly, C is a club. Hence
![]() $[id]_U\in j_U(C)$
. Then, by elementarity, for every
$[id]_U\in j_U(C)$
. Then, by elementarity, for every
![]() $\zeta <[id]_U$
, and every
$\zeta <[id]_U$
, and every
![]() $\beta _i\in s^{\prime }_\zeta $
,
$\beta _i\in s^{\prime }_\zeta $
,
![]() $i<[id]_U$
.
$i<[id]_U$
.
Let us use the fact that the sequence
![]() ${\langle } A_\alpha \mid \alpha <\kappa ^+{\rangle }$
is a strong witness for U being non-Galvin, hence
${\langle } A_\alpha \mid \alpha <\kappa ^+{\rangle }$
is a strong witness for U being non-Galvin, hence
![]() $[id]_U \not \in A^{\prime }_{\beta _\zeta }$
, for every
$[id]_U \not \in A^{\prime }_{\beta _\zeta }$
, for every
![]() $\kappa \leq \zeta < [id]_U$
. Fix any
$\kappa \leq \zeta < [id]_U$
. Fix any
![]() $\kappa \leq \xi <[id]_U$
, then by elementarity we have
$\kappa \leq \xi <[id]_U$
, then by elementarity we have
![]() in
in
![]() $M_U$
. Therefore there is some
$M_U$
. Therefore there is some
![]() $\gamma <\kappa $
such that
$\gamma <\kappa $
such that
![]() $\alpha ^{\prime }_\xi =\beta _\gamma $
. Clearly,
$\alpha ^{\prime }_\xi =\beta _\gamma $
. Clearly,
![]() $\gamma \geq \kappa $
, and by the closure property of
$\gamma \geq \kappa $
, and by the closure property of
![]() $[id]_U$
, we conclude that
$[id]_U$
, we conclude that
![]() $\gamma <[id]_U$
. Hence, in
$\gamma <[id]_U$
. Hence, in
![]() $M^*$
,
$M^*$
,
![]() $[id]_U \not \in A^{\prime }_{\beta ^{\prime }_\gamma }=A^{\prime }_{\alpha ^{\prime }_\xi }$
, as wanted.
$[id]_U \not \in A^{\prime }_{\beta ^{\prime }_\gamma }=A^{\prime }_{\alpha ^{\prime }_\xi }$
, as wanted.
Theorem 2.6. Assume GCH and let
![]() $\kappa $
be measurable in V. Then there is a cofinality preserving forcing extension
$\kappa $
be measurable in V. Then there is a cofinality preserving forcing extension
![]() $V^*$
in which there is a
$V^*$
in which there is a
![]() $\kappa $
-complete ultrafilter W over
$\kappa $
-complete ultrafilter W over
![]() $\kappa $
which concentrates on regulars, extends
$\kappa $
which concentrates on regulars, extends
![]() $Cub_\kappa $
, and has a strong witness for the failure of Galvin’s property.
$Cub_\kappa $
, and has a strong witness for the failure of Galvin’s property.
Proof The forcing is simply adding for each inaccessible
![]() $\alpha \leq \kappa $
,
$\alpha \leq \kappa $
,
![]() $\alpha ^+$
-many Cohen functions to
$\alpha ^+$
-many Cohen functions to
![]() $\alpha $
. Namely, consider the Easton support iteration
$\alpha $
. Namely, consider the Easton support iteration
such that for
![]() $\alpha \leq \kappa $
,
$\alpha \leq \kappa $
,
is trivial unless
![]() $\alpha $
is inaccessible, in which case it is a
$\alpha $
is inaccessible, in which case it is a
![]() $\mathcal {P}_\alpha $
-name for
$\mathcal {P}_\alpha $
-name for
![]() $\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)$
.
$\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)$
.
Let
![]() $G:=G_\kappa *g_\kappa $
be V-generic for
$G:=G_\kappa *g_\kappa $
be V-generic for
![]() . Denote
. Denote
![]() ${\langle } f_{\kappa ,\alpha }\mid \alpha <\kappa ^+{\rangle }$
be the enumeration of the
${\langle } f_{\kappa ,\alpha }\mid \alpha <\kappa ^+{\rangle }$
be the enumeration of the
![]() $\kappa ^+$
Cohen functions added by
$\kappa ^+$
Cohen functions added by
![]() $g_\kappa $
. The idea is that the sets which are going to be a strong witness for the failure of the Galvin property are
$g_\kappa $
. The idea is that the sets which are going to be a strong witness for the failure of the Galvin property are
![]() ${\langle } A_\alpha \mid \alpha <\kappa ^+{\rangle }$
, where
${\langle } A_\alpha \mid \alpha <\kappa ^+{\rangle }$
, where
The next step is to construct the measure for this witness by extending ground model embeddings to
![]() $V[G]$
. Let
$V[G]$
. Let
![]() $U\in V$
be a normal measure over
$U\in V$
be a normal measure over
![]() $\kappa $
and consider the second ultrapower by U and the corresponding commutative diagram
$\kappa $
and consider the second ultrapower by U and the corresponding commutative diagram
where k is simply the ultrapower embedding defined in
![]() $M_U$
using the ultrafilter
$M_U$
using the ultrafilter
![]() $j_{1}(U)$
. Denote
$j_{1}(U)$
. Denote
![]() $\kappa _1=j_1(\kappa )$
and
$\kappa _1=j_1(\kappa )$
and
![]() $\kappa _2=j_{2}(\kappa )$
, then
$\kappa _2=j_{2}(\kappa )$
, then
![]() $k(\kappa _1)=\kappa _2$
.
$k(\kappa _1)=\kappa _2$
.
By Easton support and elementarity,
where
is the quotient forcing above
![]() $\kappa $
, which is forcing equivalent to the continuation of the iteration above
$\kappa $
, which is forcing equivalent to the continuation of the iteration above
![]() $\kappa $
using the same recipe as
$\kappa $
using the same recipe as
![]() $\mathcal {P}_\kappa $
.
$\mathcal {P}_\kappa $
.
In
![]() $V[G]$
, let us first construct an M-generic filter for
$V[G]$
, let us first construct an M-generic filter for
![]() . Take
. Take
![]() $G_{\kappa }*g_{\kappa }$
to be the generic up to
$G_{\kappa }*g_{\kappa }$
to be the generic up to
![]() $\kappa $
including
$\kappa $
including
![]() $\kappa $
. Above
$\kappa $
. Above
![]() $\kappa $
, from the point of view of
$\kappa $
, from the point of view of
![]() $V[G]$
, we have
$V[G]$
, we have
![]() $\kappa ^+$
-closure for
$\kappa ^+$
-closure for
![]() $\mathcal {P}_{(\kappa ,\kappa _1)}$
. By
$\mathcal {P}_{(\kappa ,\kappa _1)}$
. By
![]() $GCH$
, and since
$GCH$
, and since
![]() $j_1$
is an ultrapower by a measure, there are only
$j_1$
is an ultrapower by a measure, there are only
![]() $\kappa ^+$
-many dense open subsets of this forcing to meet. Therefore we can construct in
$\kappa ^+$
-many dense open subsets of this forcing to meet. Therefore we can construct in
![]() $V[G]$
by standard construction an
$V[G]$
by standard construction an
![]() $M_1[G]$
-generic filter
$M_1[G]$
-generic filter
![]() $G_{(\kappa ,\kappa _1)}$
for
$G_{(\kappa ,\kappa _1)}$
for
![]() $\mathcal {P}_{(\kappa ,\kappa _1)}$
. By
$\mathcal {P}_{(\kappa ,\kappa _1)}$
. By
![]() $\kappa _1^+-cc$
of
$\kappa _1^+-cc$
of
![]() $Q_{\kappa _1}$
, we can find
$Q_{\kappa _1}$
, we can find
![]() $g^{\prime }_{\kappa _1}$
which is
$g^{\prime }_{\kappa _1}$
which is
![]() $M_1[G*G_{(\kappa ,\kappa _1)}]$
-generic for
$M_1[G*G_{(\kappa ,\kappa _1)}]$
-generic for
![]() $Q_{\kappa _1}$
. We need to change the values of
$Q_{\kappa _1}$
. We need to change the values of
![]() $g^{\prime }_{\kappa _1}={\langle } f^{\prime }_{\kappa _1,\alpha }\mid \alpha <\kappa _1^{+}{\rangle }$
to
$g^{\prime }_{\kappa _1}={\langle } f^{\prime }_{\kappa _1,\alpha }\mid \alpha <\kappa _1^{+}{\rangle }$
to
![]() $g_{\kappa _1}={\langle } f_{\kappa _1,\alpha }\mid \alpha <\kappa _1^{+}{\rangle }$
such that for every
$g_{\kappa _1}={\langle } f_{\kappa _1,\alpha }\mid \alpha <\kappa _1^{+}{\rangle }$
such that for every
![]() $\alpha <\kappa ^{+}$
,
$\alpha <\kappa ^{+}$
,
![]() $f_{\kappa _1,j_1(\alpha )}\restriction \kappa =f_{\kappa ,\alpha }$
. This will ensure that the Silver criterion to lift an elementary embedding holds, namely,
$f_{\kappa _1,j_1(\alpha )}\restriction \kappa =f_{\kappa ,\alpha }$
. This will ensure that the Silver criterion to lift an elementary embedding holds, namely,
![]() $j_1^{\prime \prime }G_{\kappa }*g\subseteq G_{\kappa }*g*G_{(\kappa ,\kappa _1)}*g^{\prime }_{\kappa _1}$
. Also, we would like to tweak the values of
$j_1^{\prime \prime }G_{\kappa }*g\subseteq G_{\kappa }*g*G_{(\kappa ,\kappa _1)}*g^{\prime }_{\kappa _1}$
. Also, we would like to tweak the values of
![]() $f_{\kappa _1,j_1(\alpha )}(\kappa )$
to ensure that the sets
$f_{\kappa _1,j_1(\alpha )}(\kappa )$
to ensure that the sets
![]() $A_\alpha $
are members of the ultrafilter generated by
$A_\alpha $
are members of the ultrafilter generated by
![]() $\kappa $
. By the definition of
$\kappa $
. By the definition of
![]() $A_\alpha $
, the way to do this is to set
$A_\alpha $
, the way to do this is to set
![]() $f_{\kappa _1,j_1(\alpha )}(\kappa )=1$
.
$f_{\kappa _1,j_1(\alpha )}(\kappa )=1$
.
Formally, for each condition
![]() $p\in \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
, define a function
$p\in \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
, define a function
![]() $p^*$
with
$p^*$
with
![]() $\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and for every
$\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and for every
![]() ${\langle } \gamma ,\alpha {\rangle }\in \operatorname {\mathrm {dom}}(p^*)$
,
${\langle } \gamma ,\alpha {\rangle }\in \operatorname {\mathrm {dom}}(p^*)$
,
 $$ \begin{align*}p^*({\langle}\gamma,\alpha{\rangle})=\begin{cases} f_{\kappa,\beta}(\gamma), & \gamma<\kappa\wedge j_1(\beta)=\alpha,\\ 1, & \gamma=\kappa\wedge j_1(\beta)=\alpha,\\ p({\langle}\gamma,\alpha{\rangle}), & \text{else}.\end{cases}\end{align*} $$
$$ \begin{align*}p^*({\langle}\gamma,\alpha{\rangle})=\begin{cases} f_{\kappa,\beta}(\gamma), & \gamma<\kappa\wedge j_1(\beta)=\alpha,\\ 1, & \gamma=\kappa\wedge j_1(\beta)=\alpha,\\ p({\langle}\gamma,\alpha{\rangle}), & \text{else}.\end{cases}\end{align*} $$
Let
![]() $g_{\kappa _1}:=\{p^*\mid p\in g^{\prime }_{\kappa _1}\}$
. Clearly, the functions
$g_{\kappa _1}:=\{p^*\mid p\in g^{\prime }_{\kappa _1}\}$
. Clearly, the functions
![]() ${\langle } f_{\kappa _1,\alpha }\mid \alpha <\kappa _1^+{\rangle }$
derived from
${\langle } f_{\kappa _1,\alpha }\mid \alpha <\kappa _1^+{\rangle }$
derived from
![]() $g_{\kappa _1}$
satisfy that
$g_{\kappa _1}$
satisfy that
![]() $f_{\kappa _1,j_1(\beta )}\restriction \kappa =f_{\kappa ,\beta }$
and
$f_{\kappa _1,j_1(\beta )}\restriction \kappa =f_{\kappa ,\beta }$
and
![]() $f_{\kappa _1,j_1(\beta )}(\kappa )=1$
for every
$f_{\kappa _1,j_1(\beta )}(\kappa )=1$
for every
![]() $\beta <\kappa ^+$
. It remains to show that
$\beta <\kappa ^+$
. It remains to show that
![]() $g_{\kappa _1}$
is generic:
$g_{\kappa _1}$
is generic:
Lemma 2.7. The filter
![]() $g_{\kappa _1}$
is
$g_{\kappa _1}$
is
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
-generic filter over
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
-generic filter over
![]() $M_1[G_{\kappa }*g*G_{(\kappa ,\kappa _1)}]$
.
$M_1[G_{\kappa }*g*G_{(\kappa ,\kappa _1)}]$
.
Proof First let us prove that
![]() $g_{\kappa _1}\subseteq \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
. Indeed,
$g_{\kappa _1}\subseteq \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
. Indeed,
![]() $g^{\prime }_{\kappa _1}\subseteq \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
and for any
$g^{\prime }_{\kappa _1}\subseteq \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
and for any
![]() $p\in g^{\prime }_{\kappa _1}$
,
$p\in g^{\prime }_{\kappa _1}$
,
and hence
![]() $\operatorname {\mathrm {dom}}(p)_{\leq \kappa }:=\{\alpha \mid \exists {\langle }\gamma ,\alpha {\rangle }\in \operatorname {\mathrm {dom}}(p),\gamma \leq \kappa \}$
is bounded in
$\operatorname {\mathrm {dom}}(p)_{\leq \kappa }:=\{\alpha \mid \exists {\langle }\gamma ,\alpha {\rangle }\in \operatorname {\mathrm {dom}}(p),\gamma \leq \kappa \}$
is bounded in
![]() $\kappa _1^+$
while
$\kappa _1^+$
while
![]() $j_1^{\prime \prime }\kappa ^+$
is unbounded. It follows that there is
$j_1^{\prime \prime }\kappa ^+$
is unbounded. It follows that there is
![]() $\theta <\kappa ^+$
such that
$\theta <\kappa ^+$
such that
Hence from the V-perspective,
![]() $|\operatorname {\mathrm {dom}}(p)_{\leq \kappa }\cap j_1^{\prime \prime }\kappa ^+|\leq \kappa $
. The difference between p and
$|\operatorname {\mathrm {dom}}(p)_{\leq \kappa }\cap j_1^{\prime \prime }\kappa ^+|\leq \kappa $
. The difference between p and
![]() $p^*$
is only on the coordinates of
$p^*$
is only on the coordinates of
![]() $\operatorname {\mathrm {dom}}(p)_{\leq \kappa }\cap j_1^{\prime \prime }\kappa ^+$
and by closure of
$\operatorname {\mathrm {dom}}(p)_{\leq \kappa }\cap j_1^{\prime \prime }\kappa ^+$
and by closure of
![]() $M_1[G_{\kappa }*g*G_{(\kappa ,\kappa _1)}]$
to
$M_1[G_{\kappa }*g*G_{(\kappa ,\kappa _1)}]$
to
![]() $\kappa $
-sequences it follows that
$\kappa $
-sequences it follows that
To see that
![]() $g_{\kappa _1}$
is generic over
$g_{\kappa _1}$
is generic over
![]() $M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]$
, let
$M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]$
, let
![]() $D\in M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]$
be dense open. In
$D\in M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]$
be dense open. In
![]() $M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]$
, define
$M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]$
, define
![]() $D^*$
to consist of all conditions
$D^*$
to consist of all conditions
![]() $p\in \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
. Such that
$p\in \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
. Such that
then
![]() $D^*$
is dense open. To see this, pick any
$D^*$
is dense open. To see this, pick any
![]() $p\in \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
and enumerate by
$p\in \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_1[G_{\kappa }*G*G_{(\kappa ,\kappa _1)}]}$
and enumerate by
![]() ${\langle } q_r\mid r<\theta {\rangle }$
all the conditions q such that
${\langle } q_r\mid r<\theta {\rangle }$
all the conditions q such that
Note
![]() $\theta <\kappa _1$
since
$\theta <\kappa _1$
since
![]() $\kappa _1$
is inaccessible in
$\kappa _1$
is inaccessible in
![]() $ M_U[G_{\kappa }*g*G_{(\kappa ,\kappa _1)}]$
. We define inductively and increasing sequence
$ M_U[G_{\kappa }*g*G_{(\kappa ,\kappa _1)}]$
. We define inductively and increasing sequence
![]() ${\langle } p_r\mid r<\theta {\rangle }$
, and exploit the
${\langle } p_r\mid r<\theta {\rangle }$
, and exploit the
![]() $\kappa _1$
-closure of
$\kappa _1$
-closure of
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
to take care of limit stages. Define
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
to take care of limit stages. Define
![]() $p_0=p$
, and suppose that
$p_0=p$
, and suppose that
![]() $p_r$
is defined, let
$p_r$
is defined, let
![]() $p_{r+1}^{\prime }:=q_r\cup p_r\restriction (\operatorname {\mathrm {dom}}(p_r)\setminus \operatorname {\mathrm {dom}}(p))$
, find
$p_{r+1}^{\prime }:=q_r\cup p_r\restriction (\operatorname {\mathrm {dom}}(p_r)\setminus \operatorname {\mathrm {dom}}(p))$
, find
![]() $p_{r+1}^{\prime }\leq t_{r+1}\in D$
which exists by density and set
$p_{r+1}^{\prime }\leq t_{r+1}\in D$
which exists by density and set
Then
![]() $p_r\leq p_{r+1}$
. Let
$p_r\leq p_{r+1}$
. Let
then
![]() $p^{*}$
has the property that for
$p^{*}$
has the property that for
![]() $\kappa $
many changes of
$\kappa $
many changes of
![]() $p^*$
from the domain of p stays inside D. Namely any q with
$p^*$
from the domain of p stays inside D. Namely any q with
![]() $\operatorname {\mathrm {dom}}(q)=\operatorname {\mathrm {dom}}(p^*)$
,
$\operatorname {\mathrm {dom}}(q)=\operatorname {\mathrm {dom}}(p^*)$
,
and
![]() $|\{x\in \operatorname {\mathrm {dom}}(p)\mid p(x)\neq q(x)\}|\leq \kappa $
,
$|\{x\in \operatorname {\mathrm {dom}}(p)\mid p(x)\neq q(x)\}|\leq \kappa $
,
![]() $q\restriction \operatorname {\mathrm {dom}}(p)=q_r$
for some r, therefore
$q\restriction \operatorname {\mathrm {dom}}(p)=q_r$
for some r, therefore
![]() $q\geq t_{r+1}\in D$
. Now we define inductively
$q\geq t_{r+1}\in D$
. Now we define inductively
![]() ${\langle } p^{(r)}\mid r<\kappa ^+{\rangle }$
,
${\langle } p^{(r)}\mid r<\kappa ^+{\rangle }$
,
![]() $p^{(0)}=p$
at limit we take union, and at successor step we take
$p^{(0)}=p$
at limit we take union, and at successor step we take
![]() $p^{(r+1)}=(p^{(r)})^*$
. We claim that
$p^{(r+1)}=(p^{(r)})^*$
. We claim that
![]() $p_*:=\cup _{r<\kappa ^+}p^{(r)}\in D^*$
. First note that
$p_*:=\cup _{r<\kappa ^+}p^{(r)}\in D^*$
. First note that
![]() $\kappa ^+<\kappa _1$
, hence
$\kappa ^+<\kappa _1$
, hence
![]() $|p_*|<\kappa _1$
(all the definition is inside
$|p_*|<\kappa _1$
(all the definition is inside
![]() $M_U[G_{\kappa }*g_{\kappa }*G_{(\kappa ,\kappa _1)}]$
). Let q be any condition with
$M_U[G_{\kappa }*g_{\kappa }*G_{(\kappa ,\kappa _1)}]$
). Let q be any condition with
![]() $\operatorname {\mathrm {dom}}(q)=\operatorname {\mathrm {dom}}(p^*)$
and denote by
$\operatorname {\mathrm {dom}}(q)=\operatorname {\mathrm {dom}}(p^*)$
and denote by
and suppose that
![]() $|I|\leq \kappa $
. Since
$|I|\leq \kappa $
. Since
![]() $\operatorname {\mathrm {dom}}(p_*)=\cup _{r<\kappa ^+}\operatorname {\mathrm {dom}}(p^{(r)})$
and
$\operatorname {\mathrm {dom}}(p_*)=\cup _{r<\kappa ^+}\operatorname {\mathrm {dom}}(p^{(r)})$
and
![]() $\operatorname {\mathrm {dom}}(p^{(r)})$
is
$\operatorname {\mathrm {dom}}(p^{(r)})$
is
![]() $\subseteq $
-increasing, there is
$\subseteq $
-increasing, there is
![]() $j<\kappa ^+$
such that
$j<\kappa ^+$
such that
![]() $I\subseteq \operatorname {\mathrm {dom}}(p^{(j)})$
. The condition
$I\subseteq \operatorname {\mathrm {dom}}(p^{(j)})$
. The condition
![]() $q\restriction I$
is enumerated in the construction of
$q\restriction I$
is enumerated in the construction of
![]() $p^{(j+1)}$
, hence
$p^{(j+1)}$
, hence
![]() $q\restriction \operatorname {\mathrm {dom}}(p^{(j+1)})\in D$
and since D is open,
$q\restriction \operatorname {\mathrm {dom}}(p^{(j+1)})\in D$
and since D is open,
![]() $q\in D$
. This means that
$q\in D$
. This means that
![]() $p_*\in D^*$
.
$p_*\in D^*$
.
Finally, by genericity of
![]() $g^{\prime }_{\kappa _1}$
, we can find
$g^{\prime }_{\kappa _1}$
, we can find
![]() $p\in D^*\cap g^{\prime }_{\kappa _1}$
. By definition,
$p\in D^*\cap g^{\prime }_{\kappa _1}$
. By definition,
![]() $p^*\in g_{\kappa _1}$
and since
$p^*\in g_{\kappa _1}$
and since
![]() $\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and
$\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and
![]() $|\{x\mid p(x)\neq p^*(x)\}|\leq \kappa $
it follows that
$|\{x\mid p(x)\neq p^*(x)\}|\leq \kappa $
it follows that
![]() $p^*\in D$
.
$p^*\in D$
.
Denote by
![]() $H=G_\kappa *g_{\kappa }*G_{(\kappa ,\kappa _1)}*g_{\kappa _1}$
, then
$H=G_\kappa *g_{\kappa }*G_{(\kappa ,\kappa _1)}*g_{\kappa _1}$
, then
![]() $j_1^{\prime \prime }G\subseteq H$
. Let
$j_1^{\prime \prime }G\subseteq H$
. Let
be the extended ultrapower and derive the normal ultrafilter over
![]() $\kappa $
,
$\kappa $
,
then
![]() $U\subseteq U_1$
and
$U\subseteq U_1$
and
![]() $j^*_1=j_{U_1}$
. Indeed let
$j^*_1=j_{U_1}$
. Indeed let
![]() $k_1:M_{U_1}\rightarrow M_1[H]$
be the usual factor map
$k_1:M_{U_1}\rightarrow M_1[H]$
be the usual factor map
![]() $k_1(j_{U_1}(f)(\kappa ))=j^*_1(f)(\kappa )$
. We will prove that
$k_1(j_{U_1}(f)(\kappa ))=j^*_1(f)(\kappa )$
. We will prove that
![]() $k_1$
is onto and therefore
$k_1$
is onto and therefore
![]() $k_1=id$
. For every
$k_1=id$
. For every
![]() $A\in M_1[H]$
, there is a name
$A\in M_1[H]$
, there is a name
such that
.
![]() $M_U$
is the ultrapower by U, hence there is
$M_U$
is the ultrapower by U, hence there is
![]() $f\in V$
such that
$f\in V$
such that
. By elementarity for every
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $f(\alpha )$
is a name. In
$f(\alpha )$
is a name. In
![]() $V[G]$
define
$V[G]$
define
![]() $f^*(\alpha )=(f(\alpha ))_G$
, then by elementarity
$f^*(\alpha )=(f(\alpha ))_G$
, then by elementarity
Denote by
![]() $M_1^*=M_1[H]$
and consider
$M_1^*=M_1[H]$
and consider
![]() $j^*_1(U_1)\in M^*_1$
. Let us now define inside
$j^*_1(U_1)\in M^*_1$
. Let us now define inside
![]() $M^*_1$
an
$M^*_1$
an
![]() $M_{2}$
-generic filter for
$M_{2}$
-generic filter for
in a similar fashion as H was defined. First we take H to be the generic for
. Note that
![]() $M_{2}$
is closed under
$M_{2}$
is closed under
![]() $\kappa _1$
-sequences with respect to
$\kappa _1$
-sequences with respect to
![]() $M_1$
. Therefore, from the
$M_1$
. Therefore, from the
![]() $M^*_1$
-point of view,
$M^*_1$
-point of view,
is
![]() $\kappa _1^+$
-closed, and we can construct an
$\kappa _1^+$
-closed, and we can construct an
![]() $M_{2}[H]$
-generic filter
$M_{2}[H]$
-generic filter
![]() $G_{(\kappa _1,\kappa _2)}*g^{\prime }_{\kappa _2}\in M_1^*$
for it. We change the values of
$G_{(\kappa _1,\kappa _2)}*g^{\prime }_{\kappa _2}\in M_1^*$
for it. We change the values of
![]() $g^{\prime }_{\kappa _2}$
a bit differently from the way we changed the values of
$g^{\prime }_{\kappa _2}$
a bit differently from the way we changed the values of
![]() $g^{\prime }_{\kappa _1}$
. If
$g^{\prime }_{\kappa _1}$
. If
![]() $\alpha <\kappa _1^+$
is of the form
$\alpha <\kappa _1^+$
is of the form
![]() $j_1(\beta )$
let
$j_1(\beta )$
let
![]() $f_{\kappa _2,k(\alpha )}(\kappa _1)=1$
(to guarantee that
$f_{\kappa _2,k(\alpha )}(\kappa _1)=1$
(to guarantee that
![]() $A_\alpha $
’s belong to the ultrafilter generated by
$A_\alpha $
’s belong to the ultrafilter generated by
![]() $\kappa _1$
) and if
$\kappa _1$
) and if
![]() $\alpha \in \kappa _1^+\setminus j_1^{\prime \prime }\kappa ^+$
letFootnote
2
$\alpha \in \kappa _1^+\setminus j_1^{\prime \prime }\kappa ^+$
letFootnote
2
![]() $f_{\kappa _2,k(\alpha )}(\kappa _1)=0$
. Also, we would like that
$f_{\kappa _2,k(\alpha )}(\kappa _1)=0$
. Also, we would like that
![]() $f_{\kappa _2,\kappa _1}(0)=\kappa $
. Formally, for every
$f_{\kappa _2,\kappa _1}(0)=\kappa $
. Formally, for every
![]() $p\in \operatorname {\mathrm {Cohen}}(\kappa _2,\kappa _2^+)^{M_2[H*G_{(\kappa _1,\kappa _2)}]}$
, define
$p\in \operatorname {\mathrm {Cohen}}(\kappa _2,\kappa _2^+)^{M_2[H*G_{(\kappa _1,\kappa _2)}]}$
, define
![]() $p^*$
to be a function with
$p^*$
to be a function with
![]() $\operatorname {\mathrm {dom}}(p)=\operatorname {\mathrm {dom}}(p^*)$
and for every
$\operatorname {\mathrm {dom}}(p)=\operatorname {\mathrm {dom}}(p^*)$
and for every
![]() ${\langle }\gamma ,\alpha {\rangle }\in \operatorname {\mathrm {dom}}(p^*)$
,
${\langle }\gamma ,\alpha {\rangle }\in \operatorname {\mathrm {dom}}(p^*)$
,
 $$ \begin{align*}p^*({\langle}\gamma,\alpha{\rangle})=\begin{cases} f_{\kappa_1,\beta}(\gamma),& \gamma<\kappa_1\wedge \alpha=k(\beta), \\ 1, & \gamma=\kappa_1\wedge \alpha=k(j_1(\beta)),\\ 0, & \gamma=\kappa_1\wedge \alpha=k(\beta),\beta\notin j_1^{\prime\prime}\kappa^+,\\ \kappa, & \gamma=0\wedge \alpha=\kappa_1,\\ p({\langle}\gamma,\alpha{\rangle}), & \text{else}.\end{cases}\end{align*} $$
$$ \begin{align*}p^*({\langle}\gamma,\alpha{\rangle})=\begin{cases} f_{\kappa_1,\beta}(\gamma),& \gamma<\kappa_1\wedge \alpha=k(\beta), \\ 1, & \gamma=\kappa_1\wedge \alpha=k(j_1(\beta)),\\ 0, & \gamma=\kappa_1\wedge \alpha=k(\beta),\beta\notin j_1^{\prime\prime}\kappa^+,\\ \kappa, & \gamma=0\wedge \alpha=\kappa_1,\\ p({\langle}\gamma,\alpha{\rangle}), & \text{else}.\end{cases}\end{align*} $$
Denote by
![]() $g_{\kappa _2}=\{p^*\mid p\in g^{\prime }_{\kappa _2}\}\in V[G]$
the resulting filter. It is important that for each
$g_{\kappa _2}=\{p^*\mid p\in g^{\prime }_{\kappa _2}\}\in V[G]$
the resulting filter. It is important that for each
![]() $p\in g^{\prime }_2$
, the set
$p\in g^{\prime }_2$
, the set
has size at most
![]() $\kappa $
. This ensured that
$\kappa $
. This ensured that
![]() $X_1\in M_1^*$
. Also,
$X_1\in M_1^*$
. Also,
![]() $k"\kappa _1^+$
is unbounded in
$k"\kappa _1^+$
is unbounded in
![]() $\kappa _2^+$
and conditions in
$\kappa _2^+$
and conditions in
![]() $\operatorname {\mathrm {Cohen}}(\kappa _2,\kappa _2^+)^{M_2[H*G_{(\kappa _1,\kappa _2)}]}$
have
$\operatorname {\mathrm {Cohen}}(\kappa _2,\kappa _2^+)^{M_2[H*G_{(\kappa _1,\kappa _2)}]}$
have
![]() $M_{2}[H*G_{(\kappa _1,\kappa _2)}]$
-cardinality less than
$M_{2}[H*G_{(\kappa _1,\kappa _2)}]$
-cardinality less than
![]() $\kappa _2$
, which guarantees that for each
$\kappa _2$
, which guarantees that for each
![]() $p\in \operatorname {\mathrm {Cohen}}(\kappa _2,\kappa _2^+)$
,
$p\in \operatorname {\mathrm {Cohen}}(\kappa _2,\kappa _2^+)$
,
has size at most
![]() $\kappa _1$
. Note that
$\kappa _1$
. Note that
![]() $p^*$
is definable in
$p^*$
is definable in
![]() $M_1^*$
from the parameters
$M_1^*$
from the parameters
![]() $p,X_1,X_2\in M_1^*$
, and
$p,X_1,X_2\in M_1^*$
, and
![]() $p^*$
differs from p at most on
$p^*$
differs from p at most on
![]() $\kappa _1$
-many values. By the closure of
$\kappa _1$
-many values. By the closure of
![]() $M_{2}[H*G_{(\kappa _1,\kappa _2)}]$
to
$M_{2}[H*G_{(\kappa _1,\kappa _2)}]$
to
![]() $\kappa _1$
-sequences from
$\kappa _1$
-sequences from
![]() $M_1^*$
,
$M_1^*$
,
The genericity argument of Lemma 2.7 extends to the models
![]() $M_1$
and
$M_1$
and
![]() $M_{2}[H*G_{(\kappa _1,\kappa _2)}]$
, hence
$M_{2}[H*G_{(\kappa _1,\kappa _2)}]$
, hence
![]() $g_{\kappa _2}$
is
$g_{\kappa _2}$
is
![]() $M_{2}[H*G_{(\kappa _1,\kappa _2)}]$
-generic. Denote by
$M_{2}[H*G_{(\kappa _1,\kappa _2)}]$
-generic. Denote by
![]() $M_2^*=M_{2}[H*G_{(\kappa _1,\kappa _2)}*g_{\kappa _2}]$
. It follows that k can be extended (in
$M_2^*=M_{2}[H*G_{(\kappa _1,\kappa _2)}*g_{\kappa _2}]$
. It follows that k can be extended (in
![]() $V[G]$
) to
$V[G]$
) to
![]() $k^*$
and also
$k^*$
and also
![]() $j_{2}$
to
$j_{2}$
to
![]() $j^*_2=k^*\circ j^*_1:V[G]\rightarrow M^*_2$
. Finally, let
$j^*_2=k^*\circ j^*_1:V[G]\rightarrow M^*_2$
. Finally, let
Let us prove that W witnesses the theorem:
Claim 2.8.
W is a
![]() $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
![]() $\kappa $
such that:
$\kappa $
such that:
-
(1)
 $j_W=j^*_2$
and
$j_W=j^*_2$
and
 $[id]_W=\kappa _1$
.
$[id]_W=\kappa _1$
. -
(2)
 $Cub_\kappa \subseteq W$
.
$Cub_\kappa \subseteq W$
. -
(3)
 $\{\alpha <\kappa \mid cf(\alpha )=\alpha \}\in W$
.
$\{\alpha <\kappa \mid cf(\alpha )=\alpha \}\in W$
. -
(4)
 ${\langle } A_\alpha \mid \alpha <\kappa ^+{\rangle }$
is a strong witness for the failure of the Galvin property.
${\langle } A_\alpha \mid \alpha <\kappa ^+{\rangle }$
is a strong witness for the failure of the Galvin property.
Proof To see (1), let us denote by
![]() $j_W:V[G]\rightarrow M_W$
the ultrapower embedding by W and
$j_W:V[G]\rightarrow M_W$
the ultrapower embedding by W and
![]() $k_W:M_W\rightarrow M^*_2$
defined by
$k_W:M_W\rightarrow M^*_2$
defined by
![]() $k_W([f]_W)=j^*_2(f)(\kappa _1)$
the factor map satisfying
$k_W([f]_W)=j^*_2(f)(\kappa _1)$
the factor map satisfying
![]() $k_W\circ j_W=j^*_2$
. Let us argue that
$k_W\circ j_W=j^*_2$
. Let us argue that
![]() $k_W$
is onto and therefore
$k_W$
is onto and therefore
![]() $k_W=id$
and
$k_W=id$
and
![]() $[id]_W=\kappa _1$
. Indeed, let
$[id]_W=\kappa _1$
. Indeed, let
![]() $A\in M_2^*$
then there is
$A\in M_2^*$
then there is
such that
. Since
![]() $j_2=j_{U^2}$
there is
$j_2=j_{U^2}$
there is
![]() $h\in V$
such that
$h\in V$
such that
. Note that
![]() $\kappa =j^*_2(f_\kappa )_{\kappa _1}(0)$
, hence define in
$\kappa =j^*_2(f_\kappa )_{\kappa _1}(0)$
, hence define in
![]() $V[G]$
,
$V[G]$
,
![]() $h^*(\alpha )=(h(f_{\kappa ,\alpha }(0),\alpha ))_G$
. We have that
$h^*(\alpha )=(h(f_{\kappa ,\alpha }(0),\alpha ))_G$
. We have that
To see
![]() $(2)$
, for every club
$(2)$
, for every club
![]() $C\in Cub_\kappa $
,
$C\in Cub_\kappa $
,
![]() $j^*_2(C)$
is closed and
$j^*_2(C)$
is closed and
![]() $j^*_1(C)$
is unbounded in
$j^*_1(C)$
is unbounded in
![]() $\kappa _1$
. Since
$\kappa _1$
. Since
![]() $crit(k^*)=\kappa _1$
and
$crit(k^*)=\kappa _1$
and
![]() $j^*_{2}(C)=k^*(j^*_1(C))$
it follows that
$j^*_{2}(C)=k^*(j^*_1(C))$
it follows that
![]() $j^*_2(C)\cap \kappa _1=j^*_1(C)$
, hence
$j^*_2(C)\cap \kappa _1=j^*_1(C)$
, hence
![]() $j^*_2(C)\cap \kappa _1$
is unbounded in
$j^*_2(C)\cap \kappa _1$
is unbounded in
![]() $\kappa _1$
which implies that
$\kappa _1$
which implies that
![]() $\kappa _1\in j^*_2(C)$
.
$\kappa _1\in j^*_2(C)$
.
For
![]() $(3)$
, since
$(3)$
, since
![]() $M_2^*\models cf(\kappa _1)=\kappa _1$
, it follows that
$M_2^*\models cf(\kappa _1)=\kappa _1$
, it follows that
![]() $\{\alpha \mid cf(\alpha )=\alpha \}\in W$
. Finally, for every
$\{\alpha \mid cf(\alpha )=\alpha \}\in W$
. Finally, for every
![]() $\alpha <\kappa ^+$
,
$\alpha <\kappa ^+$
,
Since
![]() $j_2(\alpha )=k(j_1(\alpha ))$
, by the definition of
$j_2(\alpha )=k(j_1(\alpha ))$
, by the definition of
![]() $g_{\kappa _2}$
,
$g_{\kappa _2}$
,
![]() $f_{\kappa _2,j_2(\alpha )}(\kappa _1)=1$
, thus
$f_{\kappa _2,j_2(\alpha )}(\kappa _1)=1$
, thus
![]() $\kappa _1\in j^*_2(A_\alpha )$
, and by definition of W,
$\kappa _1\in j^*_2(A_\alpha )$
, and by definition of W,
![]() $A_\alpha \in W$
.
$A_\alpha \in W$
.
For (3), let
![]() $\{A_{\alpha _i}\mid i<\kappa \}$
be any subfamily of length
$\{A_{\alpha _i}\mid i<\kappa \}$
be any subfamily of length
![]() $\kappa $
and
$\kappa $
and
![]() $\kappa \leq \eta <[id]_W=\kappa _1$
. Denote
$\kappa \leq \eta <[id]_W=\kappa _1$
. Denote
Since
![]() $\kappa \leq \eta <\kappa _1$
, then
$\kappa \leq \eta <\kappa _1$
, then
![]() $\eta \notin j_1^{\prime \prime }\kappa ^+$
and thus
$\eta \notin j_1^{\prime \prime }\kappa ^+$
and thus
![]() $\alpha ^{(1)}_\eta \notin j_1^{\prime \prime }\kappa ^+$
. Also,
$\alpha ^{(1)}_\eta \notin j_1^{\prime \prime }\kappa ^+$
. Also,
![]() $k(\alpha ^{(1)}_\eta )=\alpha ^{(2)}_{k(\eta )}=\alpha ^{(2)}_\eta $
. Hence by definition,
$k(\alpha ^{(1)}_\eta )=\alpha ^{(2)}_{k(\eta )}=\alpha ^{(2)}_\eta $
. Hence by definition,
![]() $f_{\kappa _2,\alpha ^{(2)}_\eta }(\kappa _1)=0$
, hence
$f_{\kappa _2,\alpha ^{(2)}_\eta }(\kappa _1)=0$
, hence
![]() $\kappa _1\notin A^{\prime }_{\alpha ^{(2)}_\eta }.$
$\kappa _1\notin A^{\prime }_{\alpha ^{(2)}_\eta }.$
2.2 Adding
 $\kappa ^+$
-Cohen subsets to
$\kappa ^+$
-Cohen subsets to
 $\kappa $
by Prikry forcing
$\kappa $
by Prikry forcing
In this section we will construct a model in which there is a
![]() $\kappa $
-complete ultrafilter W such that forcing with
$\kappa $
-complete ultrafilter W such that forcing with
![]() $\operatorname {\mathrm {Prikry}}(W)$
adds a generic for
$\operatorname {\mathrm {Prikry}}(W)$
adds a generic for
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
. Let us first observe that such an ultrafilter must fail to satisfy the Galvin property:
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
. Let us first observe that such an ultrafilter must fail to satisfy the Galvin property:
Proposition 2.9. If
![]() $Gal(U,\kappa ,\kappa ^+)$
holds then
$Gal(U,\kappa ,\kappa ^+)$
holds then
![]() $\operatorname {\mathrm {Prikry}}(U)$
does not add a V-generic filter for
$\operatorname {\mathrm {Prikry}}(U)$
does not add a V-generic filter for
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
.
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
.
Proof Suppose that
![]() $Gal(U,\kappa ,\kappa ^+)$
holds and let
$Gal(U,\kappa ,\kappa ^+)$
holds and let
![]() $G\subseteq \operatorname {\mathrm {Prikry}}(U)$
be V-generic. By [Reference Gitik18, Proposition 1.3] every set
$G\subseteq \operatorname {\mathrm {Prikry}}(U)$
be V-generic. By [Reference Gitik18, Proposition 1.3] every set
![]() $A\in V[G]$
of size
$A\in V[G]$
of size
![]() $\kappa ^+$
contains a set
$\kappa ^+$
contains a set
![]() $B\in V$
of cardinality
$B\in V$
of cardinality
![]() $\kappa $
. Toward a contradiction suppose that
$\kappa $
. Toward a contradiction suppose that
![]() $H\in V[G]$
is a V-generic filter for
$H\in V[G]$
is a V-generic filter for
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
. Code
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
. Code
![]() $H:\kappa \times \kappa ^+\rightarrow 2$
as
$H:\kappa \times \kappa ^+\rightarrow 2$
as
![]() $X\subseteq \kappa ^+$
, just pick a bijection
$X\subseteq \kappa ^+$
, just pick a bijection
![]() $\phi $
from
$\phi $
from
![]() $\kappa ^+$
to
$\kappa ^+$
to
![]() $\kappa ^+\times \kappa $
, and let
$\kappa ^+\times \kappa $
, and let
![]() $X=\{\alpha <\kappa ^+\mid H(\phi (\alpha ))=1\}$
. The set X does not contain an old subset of cardinality
$X=\{\alpha <\kappa ^+\mid H(\phi (\alpha ))=1\}$
. The set X does not contain an old subset of cardinality
![]() $\kappa $
; this is a contradiction. To see this, let
$\kappa $
; this is a contradiction. To see this, let
![]() $Y\in V$
such that
$Y\in V$
such that
![]() $|Y|=\kappa $
, proceed with a density argument: any condition
$|Y|=\kappa $
, proceed with a density argument: any condition
![]() $p\in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
has size
$p\in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
has size
![]() $<\kappa $
and therefore can be extended to a condition
$<\kappa $
and therefore can be extended to a condition
![]() $p'$
such that for some
$p'$
such that for some
![]() $y\in Y$
,
$y\in Y$
,
![]() $\phi (y)\in \operatorname {\mathrm {dom}}(p')$
and
$\phi (y)\in \operatorname {\mathrm {dom}}(p')$
and
![]() $p'(\phi (y))=0$
.
$p'(\phi (y))=0$
.
Hence the failure of the Galvin property is necessary.
Theorem 2.10. Assume
![]() $GCH$
and that
$GCH$
and that
![]() $\kappa $
is a measurable cardinal in V. Then there is a cofinality preserving forcing extension
$\kappa $
is a measurable cardinal in V. Then there is a cofinality preserving forcing extension
![]() $V^*$
in which
$V^*$
in which
![]() $GCH$
still holds, and there is a
$GCH$
still holds, and there is a
![]() $\kappa $
-complete ultrafilter
$\kappa $
-complete ultrafilter
![]() $U^*\in V^*$
over
$U^*\in V^*$
over
![]() $\kappa $
such that forcing with Prikry forcing
$\kappa $
such that forcing with Prikry forcing
![]() $Pikry(U^*)$
introduces a
$Pikry(U^*)$
introduces a
![]() $V^*$
-generic filter for
$V^*$
-generic filter for
![]() $Cohen^{V^*}(\kappa ,\kappa ^+)$
.
$Cohen^{V^*}(\kappa ,\kappa ^+)$
.
Proof The model
![]() $V^*$
is obtained by iterating with Easton support the lottery sum of Cohen forcings for adding
$V^*$
is obtained by iterating with Easton support the lottery sum of Cohen forcings for adding
![]() $\alpha ^+$
-Cohen functions
$\alpha ^+$
-Cohen functions
![]() ${\langle } f_{\alpha \gamma }\mid \gamma <\alpha ^+{\rangle }$
over
${\langle } f_{\alpha \gamma }\mid \gamma <\alpha ^+{\rangle }$
over
![]() $\alpha $
, and Cohen
$\alpha $
, and Cohen
![]() ${}^2$
for adding two blocks of
${}^2$
for adding two blocks of
![]() $\alpha ^+$
-Cohen functions
$\alpha ^+$
-Cohen functions
More specifically, let
denotes the Easton support iteration, such that for each
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
is the trivial forcing unless
![]() $\alpha $
is inaccessible in which case
$\alpha $
is inaccessible in which case
is a
![]() ${\mathcal P}_\alpha $
-name for the lottery sum
${\mathcal P}_\alpha $
-name for the lottery sum
At
![]() $\kappa $
itself we let
$\kappa $
itself we let
. Let
![]() $G_\kappa *F_\kappa $
be a V-generic subset of
$G_\kappa *F_\kappa $
be a V-generic subset of
and let
![]() $V^*=V[G_\kappa *F_\kappa ]$
. We denote by
$V^*=V[G_\kappa *F_\kappa ]$
. We denote by
![]() $F_\alpha :={\langle } f_{\alpha \gamma }\mid \gamma <\alpha ^+{\rangle }$
the generic Cohen function if
$F_\alpha :={\langle } f_{\alpha \gamma }\mid \gamma <\alpha ^+{\rangle }$
the generic Cohen function if
![]() $\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)$
was forced in
$\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)$
was forced in
![]() $G_\kappa $
and by
$G_\kappa $
and by
if
![]() $\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)\times \operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)$
was.
$\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)\times \operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)$
was.
Let
![]() $U\in V$
be a normal ultrafilter,
$U\in V$
be a normal ultrafilter,
![]() $j_1:=j_U:V\rightarrow M_U$
the corresponding elementary embedding,
$j_1:=j_U:V\rightarrow M_U$
the corresponding elementary embedding,
![]() $\kappa _1=j_1(\kappa )$
,
$\kappa _1=j_1(\kappa )$
,
![]() $k:=j_{j_1(U)}:M_U\rightarrow M_{U^2}$
,
$k:=j_{j_1(U)}:M_U\rightarrow M_{U^2}$
,
![]() $j_2=k\circ j_1$
, and
$j_2=k\circ j_1$
, and
![]() $\kappa _2=j_2(\kappa )$
. Let us extend
$\kappa _2=j_2(\kappa )$
. Let us extend
![]() $j_1, k,j_2$
in
$j_1, k,j_2$
in
![]() $V[G_{\kappa }*F_\kappa ]$
:
$V[G_{\kappa }*F_\kappa ]$
:
We first extend
![]() $j_{1}: V \to M_{{U}}$
to
$j_{1}: V \to M_{{U}}$
to
![]() $j_1^{*}: V[G_\kappa *F_\kappa ]\to M_{U}[G_{\kappa _1}*F_{\kappa _1}]$
. Do this by taking first
$j_1^{*}: V[G_\kappa *F_\kappa ]\to M_{U}[G_{\kappa _1}*F_{\kappa _1}]$
. Do this by taking first
![]() $G_{\kappa _1}\cap P_{\kappa }=G_\kappa $
, at
$G_{\kappa _1}\cap P_{\kappa }=G_\kappa $
, at
![]() $\kappa $
we force with the lottery sum so we can choose to force only one block of Cohens and take
$\kappa $
we force with the lottery sum so we can choose to force only one block of Cohens and take
![]() $F_\kappa $
as a generic. Then defining a master condition sequence, using the closure of the forcing above
$F_\kappa $
as a generic. Then defining a master condition sequence, using the closure of the forcing above
![]() $\kappa $
in
$\kappa $
in
![]() $M_{U}$
exploiting
$M_{U}$
exploiting
![]() $GCH$
to ensure that there are only
$GCH$
to ensure that there are only
![]() $\kappa ^+$
-many dense sets to meet. This defines
$\kappa ^+$
-many dense sets to meet. This defines
![]() $G_{\kappa _1}$
. As for
$G_{\kappa _1}$
. As for
![]() $F_{\kappa _1}$
, we first find an
$F_{\kappa _1}$
, we first find an
![]() $M_U[G_{\kappa _1}]$
-generic
$M_U[G_{\kappa _1}]$
-generic
![]() $F^{\prime }_{\kappa _1}\times H^{\prime }_{\kappa _1}\in V[G_{\kappa }*F_\kappa ]$
again using
$F^{\prime }_{\kappa _1}\times H^{\prime }_{\kappa _1}\in V[G_{\kappa }*F_\kappa ]$
again using
![]() $GCH$
, closure of
$GCH$
, closure of
![]() $M_U[G_{\kappa _1}]$
under
$M_U[G_{\kappa _1}]$
under
![]() $\kappa $
-sequences and the closure of the forcing
$\kappa $
-sequences and the closure of the forcing
![]() $(\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^2)^{M_U[G_{\kappa _1}]}$
. Let us alter some values of
$(\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^2)^{M_U[G_{\kappa _1}]}$
. Let us alter some values of
![]() $F^{\prime }_{\kappa _1}$
and
$F^{\prime }_{\kappa _1}$
and
![]() $H^{\prime }_{\kappa _1}$
to define
$H^{\prime }_{\kappa _1}$
to define
![]() $F_{\kappa _1}={\langle } f_{\kappa _1,\gamma }\mid \gamma <\kappa _1^+{\rangle }$
and
$F_{\kappa _1}={\langle } f_{\kappa _1,\gamma }\mid \gamma <\kappa _1^+{\rangle }$
and
![]() $H_{\kappa _1}={\langle } h_{\kappa _1,\gamma }\mid \gamma <\kappa _1^+{\rangle }$
such that for every
$H_{\kappa _1}={\langle } h_{\kappa _1,\gamma }\mid \gamma <\kappa _1^+{\rangle }$
such that for every
![]() $\alpha <\kappa _1^+$
:
$\alpha <\kappa _1^+$
:
-
(1)
 $f_{\kappa _1,j_1(\alpha )}\restriction \kappa =h_{\kappa _1,j_1(\alpha )}\restriction \kappa =f_{\kappa ,\alpha }$
.
$f_{\kappa _1,j_1(\alpha )}\restriction \kappa =h_{\kappa _1,j_1(\alpha )}\restriction \kappa =f_{\kappa ,\alpha }$
. -
(2)
 $f_{\kappa _1,j_1(\alpha )}(\kappa )=\alpha $
.
$f_{\kappa _1,j_1(\alpha )}(\kappa )=\alpha $
.
Formally, we change every pair of partial functions
![]() $p={\langle } p_0,p_1{\rangle } \in F^{\prime }_{\kappa _1}\times H^{\prime }_{\kappa _1}$
to the pair of partial functions
$p={\langle } p_0,p_1{\rangle } \in F^{\prime }_{\kappa _1}\times H^{\prime }_{\kappa _1}$
to the pair of partial functions
![]() $p_*={\langle } p_0^*,p_1^*{\rangle }$
such that
$p_*={\langle } p_0^*,p_1^*{\rangle }$
such that
![]() $\operatorname {\mathrm {dom}}(p_0^*)=\operatorname {\mathrm {dom}}(p_0)$
,
$\operatorname {\mathrm {dom}}(p_0^*)=\operatorname {\mathrm {dom}}(p_0)$
,
![]() $\operatorname {\mathrm {dom}}(p_1^*)=\operatorname {\mathrm {dom}}(p_1)$
and for every
$\operatorname {\mathrm {dom}}(p_1^*)=\operatorname {\mathrm {dom}}(p_1)$
and for every
![]() ${\langle } \alpha ,\delta {\rangle }\in \operatorname {\mathrm {dom}}(p_0)$
:
${\langle } \alpha ,\delta {\rangle }\in \operatorname {\mathrm {dom}}(p_0)$
:
 $$ \begin{align*}p^*_0({\langle}\alpha,\delta{\rangle})=\begin{cases} f_{\kappa,\alpha_0}(\delta), &\exists \alpha_0<\kappa^+.\alpha=j_1(\alpha_0)\text{ and }\delta<\kappa,\\ \alpha_0, & \exists \alpha_0<\kappa^+.\alpha=j_1(\alpha_0)\text{ and }\delta=\kappa,\\ p_0({\langle}\alpha,\delta{\rangle}), & \text{else}.\end{cases}\end{align*} $$
$$ \begin{align*}p^*_0({\langle}\alpha,\delta{\rangle})=\begin{cases} f_{\kappa,\alpha_0}(\delta), &\exists \alpha_0<\kappa^+.\alpha=j_1(\alpha_0)\text{ and }\delta<\kappa,\\ \alpha_0, & \exists \alpha_0<\kappa^+.\alpha=j_1(\alpha_0)\text{ and }\delta=\kappa,\\ p_0({\langle}\alpha,\delta{\rangle}), & \text{else}.\end{cases}\end{align*} $$
 $$ \begin{align*}p^*_1({\langle}\alpha,\delta{\rangle})=\begin{cases} f_{\kappa,\alpha_0}(\delta), &\exists \alpha_0<\kappa^+.\alpha=j_1(\alpha_0)\text{ and }\delta<\kappa,\\ p_1({\langle}\alpha,\delta{\rangle}), & \text{else}.\end{cases}\end{align*} $$
$$ \begin{align*}p^*_1({\langle}\alpha,\delta{\rangle})=\begin{cases} f_{\kappa,\alpha_0}(\delta), &\exists \alpha_0<\kappa^+.\alpha=j_1(\alpha_0)\text{ and }\delta<\kappa,\\ p_1({\langle}\alpha,\delta{\rangle}), & \text{else}.\end{cases}\end{align*} $$
Note that for every
![]() $p_0,p_1\subseteq \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_U[G_{\kappa _1}]}$
we only change
$p_0,p_1\subseteq \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^{M_U[G_{\kappa _1}]}$
we only change
![]() $\kappa $
-many values as
$\kappa $
-many values as
![]() $M_U[G_{\kappa _1}]\models |\operatorname {\mathrm {dom}}(p_0)|,|\operatorname {\mathrm {dom}}(p_1)|<\kappa _1$
, hence
$M_U[G_{\kappa _1}]\models |\operatorname {\mathrm {dom}}(p_0)|,|\operatorname {\mathrm {dom}}(p_1)|<\kappa _1$
, hence
since
![]() $j_1(\kappa ^+)=\bigcup j_1^{\prime \prime }\kappa ^+$
, the same holds for
$j_1(\kappa ^+)=\bigcup j_1^{\prime \prime }\kappa ^+$
, the same holds for
![]() $p_1$
. It follows that
$p_1$
. It follows that
Changing less than
![]() $\kappa _1$
-many values of a generic for
$\kappa _1$
-many values of a generic for
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^2$
does not impact the genericity. Hence
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^2$
does not impact the genericity. Hence
![]() $F_{\kappa _1}\times H_{\kappa _1}:=\{p^*\mid p\in F^{\prime }_{\kappa _1}\times H^{\prime }_{\kappa _1}\}\in V[G_{\kappa }*F_\kappa ]$
is still
$F_{\kappa _1}\times H_{\kappa _1}:=\{p^*\mid p\in F^{\prime }_{\kappa _1}\times H^{\prime }_{\kappa _1}\}\in V[G_{\kappa }*F_\kappa ]$
is still
![]() $M_U[G_{\kappa _1}]$
-generic.
$M_U[G_{\kappa _1}]$
-generic.
Since at
![]() $\kappa $
we only force
$\kappa $
we only force
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
, in order to extend
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
, in order to extend
![]() $j_1$
we only need a generic for
$j_1$
we only need a generic for
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
in the
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
in the
![]() $M_U$
-side. We constructed
$M_U$
-side. We constructed
![]() $F_{\kappa _1}$
so that
$F_{\kappa _1}$
so that
![]() $j_1^{\prime \prime }F_\kappa \subseteq F_{\kappa _1}$
, hence
$j_1^{\prime \prime }F_\kappa \subseteq F_{\kappa _1}$
, hence
![]() $j_1^{\prime \prime }G_\kappa *F_\kappa \subseteq G_{\kappa _1}*F_{\kappa _1}$
(
$j_1^{\prime \prime }G_\kappa *F_\kappa \subseteq G_{\kappa _1}*F_{\kappa _1}$
(
![]() $H_{\kappa _1}$
will be used later). Thus in
$H_{\kappa _1}$
will be used later). Thus in
![]() $V[G_{\kappa }*F_{\kappa }]$
, we have extended
$V[G_{\kappa }*F_{\kappa }]$
, we have extended
![]() $j_1\subseteq j_1^*:V[G_{\kappa }*F_{\kappa }]\rightarrow M_U[G_{\kappa _1}*F_{\kappa _1}]$
. Let us note that
$j_1\subseteq j_1^*:V[G_{\kappa }*F_{\kappa }]\rightarrow M_U[G_{\kappa _1}*F_{\kappa _1}]$
. Let us note that
![]() $j_1^*$
is actually the elementary embedding derived from the normal measure
$j_1^*$
is actually the elementary embedding derived from the normal measure
![]() $U\subseteq U^0:=\{X\in P^{V[G_\kappa *F_\kappa ]}(\kappa )\mid \kappa \in j_1^*(X)\}$
:
$U\subseteq U^0:=\{X\in P^{V[G_\kappa *F_\kappa ]}(\kappa )\mid \kappa \in j_1^*(X)\}$
:
Clearly the function
![]() $k_0:M_{U^0}\rightarrow M_U[G_{\kappa _1}*F_{\kappa _1}]$
defined by
$k_0:M_{U^0}\rightarrow M_U[G_{\kappa _1}*F_{\kappa _1}]$
defined by
![]() $k_0([f]_{U^0})=j^*_1(f)(\kappa )$
is elementary. To see the
$k_0([f]_{U^0})=j^*_1(f)(\kappa )$
is elementary. To see the
![]() $k_0=id$
let us prove that
$k_0=id$
let us prove that
![]() $k_0$
is onto. Fix
$k_0$
is onto. Fix
and let
![]() $f\in V$
be such that
$f\in V$
be such that
and define in
![]() $V[G_{\kappa }*F_\kappa ]$
the function
$V[G_{\kappa }*F_\kappa ]$
the function
![]() $f^*(x)=(f(f_{\kappa ,\kappa }(x)))_{G_{\kappa }*F_{\kappa }}$
. Then
$f^*(x)=(f(f_{\kappa ,\kappa }(x)))_{G_{\kappa }*F_{\kappa }}$
. Then
Recall that we have constructed the function
![]() $H_{\kappa _1}\in V[G_{\kappa }*F_{\kappa }]$
such that
$H_{\kappa _1}\in V[G_{\kappa }*F_{\kappa }]$
such that
![]() $F_{\kappa _1}\times H_{\kappa _1}$
is
$F_{\kappa _1}\times H_{\kappa _1}$
is
![]() $M_U[G_{\kappa _1}]$
-generic for
$M_U[G_{\kappa _1}]$
-generic for
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^2$
. Now we wish to extend
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)^2$
. Now we wish to extend
![]() $k:M_U\rightarrow M_{U^2}$
to
$k:M_U\rightarrow M_{U^2}$
to
![]() $k^*:M_U[G_{\kappa _1}*F_{\kappa _1}]\rightarrow M_{U^2}[G_{\kappa _2}*F_{\kappa _2}]$
in
$k^*:M_U[G_{\kappa _1}*F_{\kappa _1}]\rightarrow M_{U^2}[G_{\kappa _2}*F_{\kappa _2}]$
in
![]() $V[G_{\kappa }*F_{\kappa }]$
. We do this by taking
$V[G_{\kappa }*F_{\kappa }]$
. We do this by taking
![]() $G_{\kappa _2}\cap \kappa _1= G_{\kappa _1}$
, at
$G_{\kappa _2}\cap \kappa _1= G_{\kappa _1}$
, at
![]() $\kappa _1$
we force
$\kappa _1$
we force
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)\times \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
putting the generic
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)\times \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
putting the generic
![]() $F_{\kappa _1}\times H_{\kappa _1}$
, then exploiting the closure and
$F_{\kappa _1}\times H_{\kappa _1}$
, then exploiting the closure and
![]() $GCH$
to complete to a generic
$GCH$
to complete to a generic
![]() $G_{\kappa _2}*F^{\prime }_{\kappa _2}\in V[G_\kappa *F_\kappa ]$
. Finally, we wish to modify some values of
$G_{\kappa _2}*F^{\prime }_{\kappa _2}\in V[G_\kappa *F_\kappa ]$
. Finally, we wish to modify some values of
![]() $F^{\prime }_{\kappa _2}$
to a generic
$F^{\prime }_{\kappa _2}$
to a generic
![]() $F_{\kappa _2}={\langle } f_{\kappa _2,\gamma }\mid \gamma <\kappa _2^+{\rangle }$
so that for every
$F_{\kappa _2}={\langle } f_{\kappa _2,\gamma }\mid \gamma <\kappa _2^+{\rangle }$
so that for every
![]() $\alpha <\kappa _1^+$
:
$\alpha <\kappa _1^+$
:
-
(1)
 $f_{\kappa _2,k(\alpha )}\restriction \kappa _1=f_{\kappa _1,\alpha }$
.
$f_{\kappa _2,k(\alpha )}\restriction \kappa _1=f_{\kappa _1,\alpha }$
. -
(2) For
 $\alpha \in j_1^{\prime \prime }\kappa ^+$
,
$\alpha \in j_1^{\prime \prime }\kappa ^+$
,
 $f_{\kappa _2,k(\alpha )}(\kappa _1)=1$
.
$f_{\kappa _2,k(\alpha )}(\kappa _1)=1$
. -
(3) For
 $\alpha \in \kappa _1^+\setminus j_1^{\prime \prime }\kappa ^+$
,
$\alpha \in \kappa _1^+\setminus j_1^{\prime \prime }\kappa ^+$
,
 $f_{\kappa _2,k(\alpha )}(\kappa _1)=0$
.
$f_{\kappa _2,k(\alpha )}(\kappa _1)=0$
. -
(4)
 $f_{\kappa _2,\kappa _1}(\kappa _1)=\kappa $
.
$f_{\kappa _2,\kappa _1}(\kappa _1)=\kappa $
.
Again, this is possible since we do not change too many values of
![]() $F^{\prime }_{\kappa _2}$
. At this point, let us emphasize that we do not use
$F^{\prime }_{\kappa _2}$
. At this point, let us emphasize that we do not use
![]() $H_{\kappa _1}$
in the generic we have in the
$H_{\kappa _1}$
in the generic we have in the
![]() $M_U$
-side Footnote
3
. The generic
$M_U$
-side Footnote
3
. The generic
![]() $H_{\kappa _1}$
is used in the construction of the generic on the
$H_{\kappa _1}$
is used in the construction of the generic on the
![]() $M_{U^2}$
-side where we can choose (due to the lottery sum) to force at
$M_{U^2}$
-side where we can choose (due to the lottery sum) to force at
![]() $\kappa _1$
two copies of
$\kappa _1$
two copies of
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
, of course, that at
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^+)$
, of course, that at
![]() $\kappa _2=j_{2}(\kappa )$
we are still obligated to force one copy of
$\kappa _2=j_{2}(\kappa )$
we are still obligated to force one copy of
![]() $\operatorname {\mathrm {Cohen}}(\kappa _2\kappa _2^+)$
which contains the point-wise image of
$\operatorname {\mathrm {Cohen}}(\kappa _2\kappa _2^+)$
which contains the point-wise image of
![]() $F_{\kappa _1}$
under the factor map k.
$F_{\kappa _1}$
under the factor map k.
Hence we extended in
![]() $V[G_{\kappa }*F_\kappa ]$
,
$V[G_{\kappa }*F_\kappa ]$
,
![]() $k\subseteq k^*:M_U[G_{\kappa _1}*F_{\kappa _1}]\rightarrow M_{U^2}[G_{\kappa _2}*F_{\kappa _2}]$
.
$k\subseteq k^*:M_U[G_{\kappa _1}*F_{\kappa _1}]\rightarrow M_{U^2}[G_{\kappa _2}*F_{\kappa _2}]$
.

Let
![]() $j_2^*=k^*\circ j_1^*$
,
$j_2^*=k^*\circ j_1^*$
,
![]() $V^*=V[G_{\kappa }*F_\kappa ]$
,
$V^*=V[G_{\kappa }*F_\kappa ]$
,
![]() $M_1^*=M_U[G_{\kappa _1}*F_{\kappa _1}]$
and
$M_1^*=M_U[G_{\kappa _1}*F_{\kappa _1}]$
and
![]() $M_2^*=M_{U^2}[G_{\kappa _2}*F_{\kappa _2}]$
.
$M_2^*=M_{U^2}[G_{\kappa _2}*F_{\kappa _2}]$
.
In
![]() $V^*$
, define
$V^*$
, define
and for every
![]() $\alpha <\kappa ^+$
,
$\alpha <\kappa ^+$
,
Then as in Claim 2.8, we have that W is a
![]() $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
![]() $\kappa $
such that:
$\kappa $
such that:
-
(1)
 $j_1^*=j_U^*$
,
$j_1^*=j_U^*$
,
 $j^*_2=j_W$
and
$j^*_2=j_W$
and
 $[id]_W=\kappa _1$
.
$[id]_W=\kappa _1$
. -
(2)
 ${\langle } A_\alpha \mid \alpha <\kappa ^+{\rangle }$
is a strong witness for W being non-Galvin.
${\langle } A_\alpha \mid \alpha <\kappa ^+{\rangle }$
is a strong witness for W being non-Galvin. -
(3)
 $Cub_\kappa \subseteq W$
.
$Cub_\kappa \subseteq W$
. -
(4)
 $L_0=\{\alpha <\kappa \mid \operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)\times \operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)\text { was forced in }G_\kappa \}\in W$
.
$L_0=\{\alpha <\kappa \mid \operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)\times \operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)\text { was forced in }G_\kappa \}\in W$
.
Also, recall that
![]() $j_2:V\rightarrow M_2$
is also the ultrapower by
$j_2:V\rightarrow M_2$
is also the ultrapower by
![]() $U\times U$
under the identification(isomorphism):
$U\times U$
under the identification(isomorphism):
Clearly, the projections
![]() $\pi _{1},\pi _2:\kappa \times \kappa \rightarrow \kappa $
on the first and second coordinates (resp. Rudin–Keisler) project
$\pi _{1},\pi _2:\kappa \times \kappa \rightarrow \kappa $
on the first and second coordinates (resp. Rudin–Keisler) project
![]() $U^2$
on U. Also,
$U^2$
on U. Also,
![]() $W\cap V=U^*\cap V=U$
and
$W\cap V=U^*\cap V=U$
and
![]() $U^*\leq _{R-K} W$
and the projection map is denoted by
$U^*\leq _{R-K} W$
and the projection map is denoted by
![]() $\nu \mapsto \pi _{nor}(\nu )$
.Footnote
4
$\nu \mapsto \pi _{nor}(\nu )$
.Footnote
4
Let us prove that W witnesses the theorem:
Theorem 2.11. Let
![]() $H\subseteq \operatorname {\mathrm {Prikry}}(W)$
be a
$H\subseteq \operatorname {\mathrm {Prikry}}(W)$
be a
![]() $V^*$
-generic filter. There is
$V^*$
-generic filter. There is
![]() $G^*\in V^*[H]$
which is
$G^*\in V^*[H]$
which is
![]() $V^*$
-generic for
$V^*$
-generic for
![]() $Cohen(\kappa ,\kappa ^+)^{V^*}$
.
$Cohen(\kappa ,\kappa ^+)^{V^*}$
.
Proof of Theorem 2.11
Let
![]() ${\langle } c_n \mid n<\omega {\rangle } $
be the W-Prikry sequence corresponding to H. Suppose without loss of generality that for every
${\langle } c_n \mid n<\omega {\rangle } $
be the W-Prikry sequence corresponding to H. Suppose without loss of generality that for every
![]() $n<\omega $
,
$n<\omega $
,
![]() $c_n\in L_0$
, this will hold from a certain point and the proof can be adjusted in a straightforward way. This guarantees that the generic
$c_n\in L_0$
, this will hold from a certain point and the proof can be adjusted in a straightforward way. This guarantees that the generic
![]() $H_{c_n}={\langle } h_{c_n,\gamma }\mid \gamma <\alpha ^+{\rangle }$
for the second component of the generic we have in
$H_{c_n}={\langle } h_{c_n,\gamma }\mid \gamma <\alpha ^+{\rangle }$
for the second component of the generic we have in
![]() $G_\kappa $
for
$G_\kappa $
for
![]() $\operatorname {\mathrm {Cohen}}(c_n,c_n^+)\times \operatorname {\mathrm {Cohen}}(c_n,c_n^+)$
is defined for every
$\operatorname {\mathrm {Cohen}}(c_n,c_n^+)\times \operatorname {\mathrm {Cohen}}(c_n,c_n^+)$
is defined for every
![]() $n<\omega $
. The functions
$n<\omega $
. The functions
![]() $h_{c_n,\gamma }$
will be used below to define the Cohen generic functions.
$h_{c_n,\gamma }$
will be used below to define the Cohen generic functions.
Define, for every
![]() $n<\omega $
, the set
$n<\omega $
, the set
For every
![]() $\alpha <\kappa ^+$
, let
$\alpha <\kappa ^+$
, let
![]() $n_\alpha $
be the unique n such that
$n_\alpha $
be the unique n such that
![]() $\alpha \in Z_n$
. Let
$\alpha \in Z_n$
. Let
![]() $\alpha <\kappa ^+$
, and define
$\alpha <\kappa ^+$
, and define
![]() $f^*_\alpha :\kappa \to \kappa $
as follows:
$f^*_\alpha :\kappa \to \kappa $
as follows:
Fix a sequence
![]() ${\langle } s_\alpha \mid \alpha <\kappa ^+ {\rangle }\in V^*$
of canonical functions in
${\langle } s_\alpha \mid \alpha <\kappa ^+ {\rangle }\in V^*$
of canonical functions in
![]() $\prod _{\nu <\kappa }\nu ^+$
:
$\prod _{\nu <\kappa }\nu ^+$
:
Let us argue that
![]() $F={\langle } f^*_\alpha \mid \alpha <\kappa ^+{\rangle } $
induces a
$F={\langle } f^*_\alpha \mid \alpha <\kappa ^+{\rangle } $
induces a
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)^{V^*}$
generic filter over
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)^{V^*}$
generic filter over
![]() $V^*$
.
$V^*$
.
Claim 2.12. Let
![]() $G^*=\{p\in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)^{V^*}\mid p\subseteq F\}$
, then
$G^*=\{p\in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)^{V^*}\mid p\subseteq F\}$
, then
![]() $G^*$
is a
$G^*$
is a
![]() $V^*$
-generic filter.
$V^*$
-generic filter.
Let
![]() $\mathcal {A}\in V^*$
be a maximal antichain in the forcing
$\mathcal {A}\in V^*$
be a maximal antichain in the forcing
![]() $\operatorname {\mathrm {Cohen}}(\kappa , \kappa ^+)^{V^*}$
. Note that since
$\operatorname {\mathrm {Cohen}}(\kappa , \kappa ^+)^{V^*}$
. Note that since
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{+})^{V^*}$
is
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{+})^{V^*}$
is
![]() $\kappa $
-closed then
$\kappa $
-closed then
By
![]() $\kappa ^+$
-cc of the forcing
$\kappa ^+$
-cc of the forcing
![]() $\mathcal {P}_{\kappa +1}$
, there is
$\mathcal {P}_{\kappa +1}$
, there is
![]() $Y\subseteq \kappa ^{+}$
,
$Y\subseteq \kappa ^{+}$
,
![]() $Y\in V$
such that
$Y\in V$
such that
![]() $|Y|=\kappa $
and
$|Y|=\kappa $
and
![]() $\mathcal {A}\subseteq \operatorname {\mathrm {Cohen}}(\kappa ,Y)^{V^*}$
. Also, since
$\mathcal {A}\subseteq \operatorname {\mathrm {Cohen}}(\kappa ,Y)^{V^*}$
. Also, since
![]() $|\mathcal {A}|=\kappa $
,
$|\mathcal {A}|=\kappa $
,
![]() $\mathcal {A}\in V[G_\kappa *F_\kappa ]$
, there is
$\mathcal {A}\in V[G_\kappa *F_\kappa ]$
, there is
![]() $Z\subseteq \kappa ^{+}$
such that
$Z\subseteq \kappa ^{+}$
such that
![]() $|Z|=\kappa $
such that
$|Z|=\kappa $
such that
![]() $\mathcal {A}\in V[G_\kappa *F_\kappa \restriction Z]$
. Without loss of generality assume that
$\mathcal {A}\in V[G_\kappa *F_\kappa \restriction Z]$
. Without loss of generality assume that
![]() $Z=Y\in V$
(Otherwise just take the union). Let
$Z=Y\in V$
(Otherwise just take the union). Let
![]() $V\ni \phi :\kappa \rightarrow Y$
be a bijection.
$V\ni \phi :\kappa \rightarrow Y$
be a bijection.
Claim 2.13. There is an
![]() $\in $
-increasing continuous chain
$\in $
-increasing continuous chain
![]() ${\langle } N_\beta \mid \beta <\kappa {\rangle }$
of elementary submodels of
${\langle } N_\beta \mid \beta <\kappa {\rangle }$
of elementary submodels of
![]() $H_\chi $
such that:
$H_\chi $
such that:
-
(1)
 $|N_\beta |<\kappa $
.
$|N_\beta |<\kappa $
. -
(2)
 $G_\kappa ,F_\kappa ,\mathcal {A},\phi ,{\langle } s_\alpha \mid \alpha <\kappa ^+{\rangle }\in N_0$
.
$G_\kappa ,F_\kappa ,\mathcal {A},\phi ,{\langle } s_\alpha \mid \alpha <\kappa ^+{\rangle }\in N_0$
. -
(3)
 $N_\beta \cap \kappa =\gamma _\beta $
is a cardinal
$N_\beta \cap \kappa =\gamma _\beta $
is a cardinal
 $<\kappa $
,
$<\kappa $
,
 $\gamma _{\beta +1}$
is regular.
$\gamma _{\beta +1}$
is regular. -
(4) For every
 $\rho ,\delta \in \phi "\gamma _\beta .\rho <\delta \rightarrow \forall \gamma _\beta \leq \mu <\kappa , s_\rho (\mu )<s_\delta (\mu )$
.
$\rho ,\delta \in \phi "\gamma _\beta .\rho <\delta \rightarrow \forall \gamma _\beta \leq \mu <\kappa , s_\rho (\mu )<s_\delta (\mu )$
. -
(5) If
 $\gamma _\beta $
is regular, then
$\gamma _\beta $
is regular, then
 $N_\beta ^{<\gamma _\beta }\subseteq N_\beta $
. In particular
$N_\beta ^{<\gamma _\beta }\subseteq N_\beta $
. In particular
 $\operatorname {\mathrm {Cohen}}(\gamma _\beta ,\phi "\gamma _\beta )=\operatorname {\mathrm {Cohen}}(\kappa ,Y)\cap N_\beta $
.
$\operatorname {\mathrm {Cohen}}(\gamma _\beta ,\phi "\gamma _\beta )=\operatorname {\mathrm {Cohen}}(\kappa ,Y)\cap N_\beta $
.
Proof of Claim 2.13
Let us construct such a sequence inductively. Note that
![]() $(4)$
follows from elementarity and
$(4)$
follows from elementarity and
![]() $(2)$
. Requirements
$(2)$
. Requirements
![]() $(1)$
–
$(1)$
–
![]() $(5)$
are preserved at limit stages due to continuity. At successor stages, suppose we have constructed
$(5)$
are preserved at limit stages due to continuity. At successor stages, suppose we have constructed
![]() $N_\beta $
, find an elementary submodel
$N_\beta $
, find an elementary submodel
![]() $N^0_{\beta +1}$
such that
$N^0_{\beta +1}$
such that
![]() $N_\beta \subseteq N^0_{\beta +1}, \ {\langle } N_\alpha \mid \alpha <\beta {\rangle }\in N^0_{\beta +1}$
, then we construct an auxiliary
$N_\beta \subseteq N^0_{\beta +1}, \ {\langle } N_\alpha \mid \alpha <\beta {\rangle }\in N^0_{\beta +1}$
, then we construct an auxiliary
![]() $\in $
-increasing and continuous chain of elementary submodels
$\in $
-increasing and continuous chain of elementary submodels
![]() ${\langle } N^\alpha _{\beta +1}\mid \alpha <\kappa {\rangle }$
as follows:
${\langle } N^\alpha _{\beta +1}\mid \alpha <\kappa {\rangle }$
as follows:
![]() $N^0_{\beta +1}$
is already defined. At limits we take the union and at successor let us take care of requirements 3 and 5. Let
$N^0_{\beta +1}$
is already defined. At limits we take the union and at successor let us take care of requirements 3 and 5. Let
![]() $\gamma ^{\prime }_\alpha =\sup (N^{\alpha }_{\beta +1}\cap \kappa )<\kappa $
. Let
$\gamma ^{\prime }_\alpha =\sup (N^{\alpha }_{\beta +1}\cap \kappa )<\kappa $
. Let
![]() $N^{\alpha +1}_{\beta +1}$
be an elementary submodel such that
$N^{\alpha +1}_{\beta +1}$
be an elementary submodel such that
![]() $N^{\alpha }_\beta ,^{<\gamma ^{\prime }_\alpha },\subseteq N^{\alpha +1}_{\beta +1}$
and
$N^{\alpha }_\beta ,^{<\gamma ^{\prime }_\alpha },\subseteq N^{\alpha +1}_{\beta +1}$
and
![]() $|N^{\alpha +1}_{\beta +1}|<\kappa $
. Note that the sets
$|N^{\alpha +1}_{\beta +1}|<\kappa $
. Note that the sets
are clubs and also
![]() $\bar C=C_1\cap C_2$
is. It follows that
$\bar C=C_1\cap C_2$
is. It follows that
![]() $\{\gamma ^{\prime }_\alpha \mid \alpha \in \bar C\}$
is a club and since
$\{\gamma ^{\prime }_\alpha \mid \alpha \in \bar C\}$
is a club and since
![]() $\kappa $
is measurable, there is a
$\kappa $
is measurable, there is a
![]() $\alpha ^*\in \bar C$
limit such that
$\alpha ^*\in \bar C$
limit such that
![]() $\gamma ^{\prime }_{\alpha ^*}$
is regular. Let
$\gamma ^{\prime }_{\alpha ^*}$
is regular. Let
![]() $N_{\beta +1}=N^{\alpha ^*}_{\beta +1}$
, to conclude
$N_{\beta +1}=N^{\alpha ^*}_{\beta +1}$
, to conclude
![]() $2$
since
$2$
since
![]() $\gamma _{\beta +1}=\gamma ^{\prime }_{\alpha ^*}$
is regular.
$\gamma _{\beta +1}=\gamma ^{\prime }_{\alpha ^*}$
is regular.
Set
This is club in
![]() $\kappa $
since the sequence
$\kappa $
since the sequence
![]() $\gamma _\beta $
is continuous and since the set
$\gamma _\beta $
is continuous and since the set
![]() $\{\beta \mid \gamma _\beta =\beta \}$
is a club.
$\{\beta \mid \gamma _\beta =\beta \}$
is a club.
Claim 2.14. Let
Then
![]() $E\in W$
.
$E\in W$
.
Proof of Claim 2.14
By construction, for every
![]() $\alpha <\kappa _1^{+}$
,
$\alpha <\kappa _1^{+}$
,
![]() $f_{\kappa _2,k(\alpha )}\restriction \kappa _1=f_{\kappa _1,\alpha }$
and therefore for every
$f_{\kappa _2,k(\alpha )}\restriction \kappa _1=f_{\kappa _1,\alpha }$
and therefore for every
![]() $\alpha \in j^*_2(\phi )"\kappa _1$
, there is
$\alpha \in j^*_2(\phi )"\kappa _1$
, there is
![]() $\nu <\kappa _1^+$
such that
$\nu <\kappa _1^+$
such that
![]() $\alpha =k^*(j_1^*(\phi ))(\nu )=k^*(j_1^*(\phi )(\nu ))$
and
$\alpha =k^*(j_1^*(\phi ))(\nu )=k^*(j_1^*(\phi )(\nu ))$
and
![]() $j_1^*(\phi )(\nu )<\kappa _1^{+}$
. Hence
$j_1^*(\phi )(\nu )<\kappa _1^{+}$
. Hence
![]() $f_{\kappa _2,\alpha }\restriction \kappa _1=f_{\kappa _1,\beta }$
for some
$f_{\kappa _2,\alpha }\restriction \kappa _1=f_{\kappa _1,\beta }$
for some
![]() $\beta <\kappa _1^{+}$
. Reflecting this we obtain the set
$\beta <\kappa _1^{+}$
. Reflecting this we obtain the set
![]() $E\in W$
.
$E\in W$
.
To see that
![]() $G^*\cap \mathcal {A}\neq \emptyset $
, we will need to catch a piece of
$G^*\cap \mathcal {A}\neq \emptyset $
, we will need to catch a piece of
![]() $\mathcal {A}$
in the elementary submodels constructed and pick the Prikry points in the club C prepared:
$\mathcal {A}$
in the elementary submodels constructed and pick the Prikry points in the club C prepared:
Claim 2.15. For every
![]() $\nu _0\in C\cap E$
, there is
$\nu _0\in C\cap E$
, there is
![]() $d=d^{\nu _0}\in N_{\nu _0}\cap \mathcal {A}$
such that d is extended by
$d=d^{\nu _0}\in N_{\nu _0}\cap \mathcal {A}$
such that d is extended by
![]() ${\langle } h_{\nu _0,s_{\tau }(\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
.
${\langle } h_{\nu _0,s_{\tau }(\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
.
Proof of Claim 2.15
Fix any
![]() $\nu _0\in C\cap E$
. Consider the transitive collapse of
$\nu _0\in C\cap E$
. Consider the transitive collapse of
![]() $\pi :N_{\nu _0}\rightarrow N_{\nu _0}^*$
. Then the critical point of
$\pi :N_{\nu _0}\rightarrow N_{\nu _0}^*$
. Then the critical point of
![]() $\pi ^{-1}:N_{\nu _0}^*\rightarrow N_{\nu _0}$
is
$\pi ^{-1}:N_{\nu _0}^*\rightarrow N_{\nu _0}$
is
![]() $\nu _0$
and
$\nu _0$
and
![]() $\pi ^{-1}(\nu _0)=\kappa $
. Denote by
$\pi ^{-1}(\nu _0)=\kappa $
. Denote by
![]() $\overline {F}_\kappa =\pi (F_\kappa ), \overline {\phi }=\pi (\phi )$
. Denote
$\overline {F}_\kappa =\pi (F_\kappa ), \overline {\phi }=\pi (\phi )$
. Denote
![]() $\overline {F}_\kappa ={\langle } \overline {f}_{\kappa ,\gamma }\mid \gamma < \pi (\kappa ^+){\rangle }$
. For every
$\overline {F}_\kappa ={\langle } \overline {f}_{\kappa ,\gamma }\mid \gamma < \pi (\kappa ^+){\rangle }$
. For every
![]() $\gamma \in \overline {\phi }"{\nu _0}$
, there is some
$\gamma \in \overline {\phi }"{\nu _0}$
, there is some
![]() $\delta <{\nu _0}$
such that
$\delta <{\nu _0}$
such that
Moreover, since
![]() ${\nu _0}\in E$
,
${\nu _0}\in E$
,
![]() $f_{\kappa ,\phi (\delta )}\restriction {\nu _0}=f_{{\nu _0},\rho }$
for some
$f_{\kappa ,\phi (\delta )}\restriction {\nu _0}=f_{{\nu _0},\rho }$
for some
![]() $\rho <{\nu _0}^{+}$
and therefore
$\rho <{\nu _0}^{+}$
and therefore
![]() $\overline {f}_{\kappa ,\gamma }=f_{{\nu _0},\rho }$
. Recall that
$\overline {f}_{\kappa ,\gamma }=f_{{\nu _0},\rho }$
. Recall that
, hence
. We conclude that for some subset
![]() $Z\subseteq {\nu _0}^{+}$
,
$Z\subseteq {\nu _0}^{+}$
,
Since
![]() ${\nu _0}\in L_0$
, in
${\nu _0}\in L_0$
, in
![]() $V[G_{\kappa }*F_\kappa ]$
we also have
$V[G_{\kappa }*F_\kappa ]$
we also have
![]() $H_{\nu _0}={\langle } h_{\nu _0,\alpha }\mid \alpha <\nu _0^+{\rangle }$
which are mutually Cohen-generic over
$H_{\nu _0}={\langle } h_{\nu _0,\alpha }\mid \alpha <\nu _0^+{\rangle }$
which are mutually Cohen-generic over
![]() $V[G_{\nu _0}*F_{\nu _0}\restriction Z]$
.
$V[G_{\nu _0}*F_{\nu _0}\restriction Z]$
.
By construction,
![]() $\forall \tau _1<\tau _2\in \phi "\nu _0$
,
$\forall \tau _1<\tau _2\in \phi "\nu _0$
,
![]() $s_{\tau _1}(\nu _0)<s_{\tau _2}(\nu _0)$
, hence
$s_{\tau _1}(\nu _0)<s_{\tau _2}(\nu _0)$
, hence
![]() ${\langle } h_{\nu _0,s_\tau (\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
are Cohen functions over
${\langle } h_{\nu _0,s_\tau (\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
are Cohen functions over
![]() $\nu _0$
which are distinct mutually
$\nu _0$
which are distinct mutually
![]() $V[G_{\nu _0}*F_{\nu _0}\restriction Z]$
-generic. Also,
$V[G_{\nu _0}*F_{\nu _0}\restriction Z]$
-generic. Also,
![]() $\overline {\mathcal {A}}\subseteq \pi (\operatorname {\mathrm {Cohen}}(\kappa ,Y))= \operatorname {\mathrm {Cohen}}(\nu _0,\pi (\phi )"\nu _0)=\operatorname {\mathrm {Cohen}}(\nu _0,\pi "[\phi "\nu _0])$
is a maximal antichain. Since
$\overline {\mathcal {A}}\subseteq \pi (\operatorname {\mathrm {Cohen}}(\kappa ,Y))= \operatorname {\mathrm {Cohen}}(\nu _0,\pi (\phi )"\nu _0)=\operatorname {\mathrm {Cohen}}(\nu _0,\pi "[\phi "\nu _0])$
is a maximal antichain. Since
![]() $|\pi "\phi "\nu _0|=\nu _0=|\phi "\nu _0|$
, we can change the enumeration of the functions
$|\pi "\phi "\nu _0|=\nu _0=|\phi "\nu _0|$
, we can change the enumeration of the functions
![]() ${\langle } h_{\nu _0,s_{\tau }(\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
to
${\langle } h_{\nu _0,s_{\tau }(\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
to
![]() $h^{\prime }_{\pi (\tau )}=h_{\nu _0,s_{\tau }(\nu _0)}$
so that
$h^{\prime }_{\pi (\tau )}=h_{\nu _0,s_{\tau }(\nu _0)}$
so that
![]() ${\langle } h^{\prime }_{\rho }\mid \rho \in \pi "\phi "\nu _0{\rangle }$
is generic for
${\langle } h^{\prime }_{\rho }\mid \rho \in \pi "\phi "\nu _0{\rangle }$
is generic for
![]() $\operatorname {\mathrm {Cohen}}(\nu _0,\pi "\phi _0)$
. Thus pick
$\operatorname {\mathrm {Cohen}}(\nu _0,\pi "\phi _0)$
. Thus pick
![]() $d_0 \in \overline {\mathcal {A}}$
such that
$d_0 \in \overline {\mathcal {A}}$
such that
![]() $d_0$
is extended by
$d_0$
is extended by
![]() ${\langle } h^{\prime }_{\rho }\mid \rho \in \pi "\phi "\nu _0{\rangle }$
. It follows that
${\langle } h^{\prime }_{\rho }\mid \rho \in \pi "\phi "\nu _0{\rangle }$
. It follows that
is a condition with
![]() $\operatorname {\mathrm {dom}}(d)=\pi ^{-1}(\operatorname {\mathrm {dom}}(d_0))$
. Since the critical point of
$\operatorname {\mathrm {dom}}(d)=\pi ^{-1}(\operatorname {\mathrm {dom}}(d_0))$
. Since the critical point of
![]() $\pi $
is
$\pi $
is
![]() $\nu _0$
, for every
$\nu _0$
, for every
![]() ${\langle }\alpha ,\beta {\rangle }\in \operatorname {\mathrm {dom}}(d_0)$
,
${\langle }\alpha ,\beta {\rangle }\in \operatorname {\mathrm {dom}}(d_0)$
,
![]() $\pi ^{-1}({\langle }\alpha ,\beta {\rangle }))={\langle }\alpha ,\pi ^{-1}(\beta ){\rangle }$
, hence
$\pi ^{-1}({\langle }\alpha ,\beta {\rangle }))={\langle }\alpha ,\pi ^{-1}(\beta ){\rangle }$
, hence
In particular for every
![]() ${\langle }\gamma ,\alpha {\rangle }\in \operatorname {\mathrm {dom}}(d)$
,
${\langle }\gamma ,\alpha {\rangle }\in \operatorname {\mathrm {dom}}(d)$
,
Thus d is extended by
![]() ${\langle } h_{\nu _0,s_\tau (\nu _0)}\mid \tau \in \phi "\nu _0 {\rangle }$
.
${\langle } h_{\nu _0,s_\tau (\nu _0)}\mid \tau \in \phi "\nu _0 {\rangle }$
.
It suffices to show that any condition in
![]() $\operatorname {\mathrm {Prikry}}(W)$
has an extension which forces that
$\operatorname {\mathrm {Prikry}}(W)$
has an extension which forces that
![]() $G^*$
meets a member of
$G^*$
meets a member of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Let
![]() $p={\langle } {\langle }{\rangle }, B{\rangle }$
be a condition (we assume for simplicity that its finite sequence is empty) and shrink B to
$p={\langle } {\langle }{\rangle }, B{\rangle }$
be a condition (we assume for simplicity that its finite sequence is empty) and shrink B to
![]() $B\cap C\cap E$
. For any
$B\cap C\cap E$
. For any
![]() $\nu _0\in B\cap C\cap E$
, we split
$\nu _0\in B\cap C\cap E$
, we split
![]() $\phi "\nu _0$
into two sets:
$\phi "\nu _0$
into two sets:
The condition
![]() $p_0={\langle } {\langle } \nu _0{\rangle }, B\cap C\cap E\cap X\cap (\bigcap _{\tau \in \phi "\nu _0}A_\tau ){\rangle }$
forces the following:
$p_0={\langle } {\langle } \nu _0{\rangle }, B\cap C\cap E\cap X\cap (\bigcap _{\tau \in \phi "\nu _0}A_\tau ){\rangle }$
forces the following:
-
(1) The Prikry sequence is included in each
 $A_\tau $
,
$A_\tau $
,
 $\tau \in X^{\nu _0}_0$
, i.e.,
$\tau \in X^{\nu _0}_0$
, i.e.,
 $n_\tau =0$
.
$n_\tau =0$
. -
(2)
 $n_\tau =1$
, for every
$n_\tau =1$
, for every
 $\tau \in X^{\nu _0}_1$
.
$\tau \in X^{\nu _0}_1$
.
In particular, this condition forces some information about the Cohen functions. Namely that:
-
(1) For
 $\tau \in X_0^{\nu _0}$
,
$\tau \in X_0^{\nu _0}$
,
 $f^*_{\tau }\restriction \nu _0=h_{\nu _0,s_\tau (\nu _0)}.$
$f^*_{\tau }\restriction \nu _0=h_{\nu _0,s_\tau (\nu _0)}.$
-
(2) For
 $\tau \in X_1^{\nu _0}$
,
$\tau \in X_1^{\nu _0}$
,
 .
.
We would like to find a condition in
![]() $\mathcal {A}$
which is below these decided parts of the Cohen. By the previous proposition, there is
$\mathcal {A}$
which is below these decided parts of the Cohen. By the previous proposition, there is
![]() $d\in N_{\nu _0}\cap \operatorname {\mathrm {Cohen}}(\kappa ,Y)=\operatorname {\mathrm {Cohen}}(\nu _0,\phi "\nu _0)$
, which is extended by
$d\in N_{\nu _0}\cap \operatorname {\mathrm {Cohen}}(\kappa ,Y)=\operatorname {\mathrm {Cohen}}(\nu _0,\phi "\nu _0)$
, which is extended by
![]() ${\langle } h_{\nu _0,s_\tau (\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
. However, by
${\langle } h_{\nu _0,s_\tau (\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
. However, by
![]() $(1)$
and
$(1)$
and
![]() $(2)$
we can only ensure that the generic
$(2)$
we can only ensure that the generic
![]() $f^*_\tau $
to extend
$f^*_\tau $
to extend
![]() $d\restriction \nu _0\times X^{\nu _0}_0$
in
$d\restriction \nu _0\times X^{\nu _0}_0$
in
![]() $X^{\nu _0}_0$
. We are left to extend
$X^{\nu _0}_0$
. We are left to extend
![]() $d\restriction \nu _0\times X^{\nu _0}_1$
. Let us show that for many
$d\restriction \nu _0\times X^{\nu _0}_1$
. Let us show that for many
![]() $\nu _0$
,
$\nu _0$
,
![]() $X^{\nu }_0$
is a relatively large subset of
$X^{\nu }_0$
is a relatively large subset of
![]() $\phi "\nu _0$
:
$\phi "\nu _0$
:
Claim 2.16. Let
Then
![]() $R\in W$
.
$R\in W$
.
Proof Clearly, for every
![]() $\alpha \in j^*_2(\phi )"\kappa $
,
$\alpha \in j^*_2(\phi )"\kappa $
,
![]() $\alpha =j^*_2(\phi (\gamma ))$
, and
$\alpha =j^*_2(\phi (\gamma ))$
, and
![]() $f_{\kappa _2,\alpha }(\kappa _1)=1$
, reflecting this, we can find a W-large set of
$f_{\kappa _2,\alpha }(\kappa _1)=1$
, reflecting this, we can find a W-large set of
![]() $\nu $
’s such that for every
$\nu $
’s such that for every
![]() $\alpha \in \phi "\pi _{nor}(\nu )$
,
$\alpha \in \phi "\pi _{nor}(\nu )$
,
![]() $f_{\kappa ,\alpha }(\nu )=1$
. And by definition of
$f_{\kappa ,\alpha }(\nu )=1$
. And by definition of
![]() $A_\alpha $
,
$A_\alpha $
,
![]() $\nu \in A_\alpha $
.
$\nu \in A_\alpha $
.
Denote
![]() $B_0:=B\cap C\cap E\cap R$
. In order to extend
$B_0:=B\cap C\cap E\cap R$
. In order to extend
![]() $d\restriction \nu _0\times X_1$
, we will need to pick
$d\restriction \nu _0\times X_1$
, we will need to pick
![]() $\nu _0$
high enough in
$\nu _0$
high enough in
![]() $B_0$
, but also the next point
$B_0$
, but also the next point
![]() $\nu _1\in B_0\setminus \nu _0+1$
in the Prikry sequence such that it will belong to all
$\nu _1\in B_0\setminus \nu _0+1$
in the Prikry sequence such that it will belong to all
![]() $A_\tau $
with
$A_\tau $
with
![]() $\tau \in X_1$
and in addition the relevant Cohen functions over
$\tau \in X_1$
and in addition the relevant Cohen functions over
![]() $\nu _1$
extend
$\nu _1$
extend
![]() $d\restriction \nu _0\times X_1$
.
$d\restriction \nu _0\times X_1$
.
Let us look at
![]() $B_0$
more carefully. Let
$B_0$
more carefully. Let
be its name in V. We fix a condition
![]() $m_0\in G_\kappa *F_\kappa $
which forces that if
$m_0\in G_\kappa *F_\kappa $
which forces that if
then the properties of Claims 2.15 and 2.16 hold, namely there is
which is extended by
, and
. Recall that by the construction of
![]() $G_{\kappa _2}$
, we have
$G_{\kappa _2}$
, we have
![]() $m_0\in G_{\kappa _2}*F_{\kappa _2}$
. Let
$m_0\in G_{\kappa _2}*F_{\kappa _2}$
. Let
![]() $ m_0\leq t\in G_{\kappa _2}*F_{\kappa _2}$
be a condition such that
$ m_0\leq t\in G_{\kappa _2}*F_{\kappa _2}$
be a condition such that
By the construction of
![]() $G_{\kappa _2}*F_{\kappa _2}$
, t has the form:
$G_{\kappa _2}*F_{\kappa _2}$
, t has the form:
 $$ \begin{align*}t={\langle} t_{<\kappa}, t_{\kappa},t_{(\kappa,\kappa_1)},\underset{t_{\kappa_1}}{\underbrace{{\langle} t_{\kappa_1}^0,t_{\kappa_1}^1{\rangle}}},t_{(\kappa_1,\kappa_2)},t_{\kappa_2}{\rangle}.\end{align*} $$
$$ \begin{align*}t={\langle} t_{<\kappa}, t_{\kappa},t_{(\kappa,\kappa_1)},\underset{t_{\kappa_1}}{\underbrace{{\langle} t_{\kappa_1}^0,t_{\kappa_1}^1{\rangle}}},t_{(\kappa_1,\kappa_2)},t_{\kappa_2}{\rangle}.\end{align*} $$
Since
![]() $f_{\kappa _2,j_2(\alpha )}(\kappa _1)=1$
for every
$f_{\kappa _2,j_2(\alpha )}(\kappa _1)=1$
for every
![]() $\alpha <\kappa ^+$
, this will hold for every
$\alpha <\kappa ^+$
, this will hold for every
![]() $\alpha \in \phi "\kappa $
as well. Also, recall that
$\alpha \in \phi "\kappa $
as well. Also, recall that
![]() $Y\in V$
, hence
$Y\in V$
, hence
![]() $\phi \in V$
. Thus
$\phi \in V$
. Thus
![]() $j_2(\phi )\in M_2$
and
$j_2(\phi )\in M_2$
and
![]() $j_2(\phi )"\kappa \in M_2$
. Also, for
$j_2(\phi )"\kappa \in M_2$
. Also, for
![]() $(t_{\kappa _2})_{G_{\kappa _2}}\in M_2[G_{\kappa _2}]$
,
$(t_{\kappa _2})_{G_{\kappa _2}}\in M_2[G_{\kappa _2}]$
,
and
![]() $(t_{\kappa _2})_{G_{\kappa _2}}\restriction \kappa \times \{j_2(\alpha )\}\subseteq f_{\kappa ,\alpha }$
. We also fix
$(t_{\kappa _2})_{G_{\kappa _2}}\restriction \kappa \times \{j_2(\alpha )\}\subseteq f_{\kappa ,\alpha }$
. We also fix
![]() $\theta <\kappa ^+$
such that
$\theta <\kappa ^+$
such that
![]() $\operatorname {\mathrm {Supp}}((t_{\kappa _2})_{G_{\kappa _2}})\subseteq j_2(\theta )$
, there is such
$\operatorname {\mathrm {Supp}}((t_{\kappa _2})_{G_{\kappa _2}})\subseteq j_2(\theta )$
, there is such
![]() $\theta $
since
$\theta $
since
![]() $j_2^{\prime \prime }\kappa ^+$
is unbounded in
$j_2^{\prime \prime }\kappa ^+$
is unbounded in
![]() $j_2(\kappa ^+)$
. Therefore, we can extend if necessary t such that
$j_2(\kappa ^+)$
. Therefore, we can extend if necessary t such that
Next consider
![]() $t_{\kappa _1}={\langle } t_{\kappa _1}^0,t_{\kappa _1}^1{\rangle }$
; it is a
$t_{\kappa _1}={\langle } t_{\kappa _1}^0,t_{\kappa _1}^1{\rangle }$
; it is a
![]() ${\mathcal P}_{\kappa _1}$
-name for a condition in
${\mathcal P}_{\kappa _1}$
-name for a condition in
![]() $F_{\kappa _1}\times H_{\kappa _1}$
. By the construction of the generic
$F_{\kappa _1}\times H_{\kappa _1}$
. By the construction of the generic
![]() $F_{\kappa _1}\times H_{\kappa _1}$
, for every
$F_{\kappa _1}\times H_{\kappa _1}$
, for every
![]() $\alpha <\kappa ^+$
, we made sure that
$\alpha <\kappa ^+$
, we made sure that
![]() $h_{\kappa _1,j_1(\alpha )}\restriction \kappa =f_{\kappa ,\alpha }$
. Also,
$h_{\kappa _1,j_1(\alpha )}\restriction \kappa =f_{\kappa ,\alpha }$
. Also,
![]() $j_1(\phi )"\kappa \in M_2$
. Let
$j_1(\phi )"\kappa \in M_2$
. Let
Note that for every
![]() $\beta <\kappa ^+$
,
$\beta <\kappa ^+$
,
![]() $j_1(s_\beta )=s_{j_1(\beta )}:\kappa _1\rightarrow \kappa _1$
is the canonical function for
$j_1(s_\beta )=s_{j_1(\beta )}:\kappa _1\rightarrow \kappa _1$
is the canonical function for
![]() $j_1(\beta )$
defined in
$j_1(\beta )$
defined in
![]() $M_U$
, hence
$M_U$
, hence
![]() $j_2(s_\beta )(\kappa _1)=k(s_{j_1(\beta )})(\kappa _1)=j_1(\beta )$
. Hence
$j_2(s_\beta )(\kappa _1)=k(s_{j_1(\beta )})(\kappa _1)=j_1(\beta )$
. Hence
Extend if necessary
![]() $t_{<\kappa _1}$
, and assume that
$t_{<\kappa _1}$
, and assume that
As for the lower part, due to the Easton support, we have
Fix functions
![]() $r,\Gamma _1$
which represents
$r,\Gamma _1$
which represents
![]() $t,\mu $
resp. in the ultrapower
$t,\mu $
resp. in the ultrapower
![]() $M_{U^2}$
, namely
$M_{U^2}$
, namely
![]() $j_2(r)(\kappa ,\kappa _1)=t, \ j_2(\Gamma _1)(\kappa ,\kappa _1)=\mu $
. Without loss of generality, suppose that for every
$j_2(r)(\kappa ,\kappa _1)=t, \ j_2(\Gamma _1)(\kappa ,\kappa _1)=\mu $
. Without loss of generality, suppose that for every
![]() $(\nu ',\nu )$
, it takes the form
$(\nu ',\nu )$
, it takes the form
Reflecting some of the properties of t we obtain a set
![]() $B'\in U^2$
such that for every
$B'\in U^2$
such that for every
![]() $(\nu ',\nu )\in B'$
:
$(\nu ',\nu )\in B'$
:
-
 $(1)_{(\nu ',\nu )}$
$(1)_{(\nu ',\nu )}$
 .
. -
 $(2a)_{(\nu ',\nu )}$
$(2a)_{(\nu ',\nu )}$
 $ r_{<\kappa }\Vdash (\nu '\cup \{\nu \})\times \phi "\nu '\hspace{-1pt} \subseteq\hspace{-1pt} \operatorname {\mathrm {dom}}(r_{\kappa })\wedge {\langle }0,\nu {\rangle }\in \operatorname {\mathrm {dom}}(r_{\kappa })\wedge \operatorname {\mathrm {Supp}}(r_{\kappa }) \subseteq \theta .$
$ r_{<\kappa }\Vdash (\nu '\cup \{\nu \})\times \phi "\nu '\hspace{-1pt} \subseteq\hspace{-1pt} \operatorname {\mathrm {dom}}(r_{\kappa })\wedge {\langle }0,\nu {\rangle }\in \operatorname {\mathrm {dom}}(r_{\kappa })\wedge \operatorname {\mathrm {Supp}}(r_{\kappa }) \subseteq \theta .$
-
 $(2b)_{(\nu ',\nu )}$
$(2b)_{(\nu ',\nu )}$
 $r_{<\kappa }\Vdash \forall \alpha \in \phi "\nu '.r_{\kappa ,\alpha }(\nu )=1$
and
$r_{<\kappa }\Vdash \forall \alpha \in \phi "\nu '.r_{\kappa ,\alpha }(\nu )=1$
and
 $r_{\kappa ,\nu }(0)=\nu '$
.
$r_{\kappa ,\nu }(0)=\nu '$
. -
 $(3)_{(\nu ',\nu )}$
$(3)_{(\nu ',\nu )}$
 $ r_{<\nu }\Vdash \nu '\times \operatorname {\mathrm {dom}}(\Gamma _1(\nu ',\nu ))\hspace{-1pt}\subseteq\hspace{-1pt} \operatorname {\mathrm {dom}}(r^1_\nu )$
and for every
$ r_{<\nu }\Vdash \nu '\times \operatorname {\mathrm {dom}}(\Gamma _1(\nu ',\nu ))\hspace{-1pt}\subseteq\hspace{-1pt} \operatorname {\mathrm {dom}}(r^1_\nu )$
and for every
 .
. -
 $(4)_{(\nu ',\nu )}$
$(4)_{(\nu ',\nu )}$
 $r_{<\nu '}=t_{<\kappa }\in V_{\nu '}$
.
$r_{<\nu '}=t_{<\kappa }\in V_{\nu '}$
.
Let
Since
![]() $B'\in U^2$
we have that
$B'\in U^2$
we have that
![]() $(\kappa ,\kappa _1)\in j_2(B')$
and since
$(\kappa ,\kappa _1)\in j_2(B')$
and since
![]() $j_2(r)(\kappa ,\kappa _1)=t\in j^*_2(G_\kappa *F_\kappa )=G_{\kappa _2}*F_{\kappa _2}$
, we conclude that
$j_2(r)(\kappa ,\kappa _1)=t\in j^*_2(G_\kappa *F_\kappa )=G_{\kappa _2}*F_{\kappa _2}$
, we conclude that
![]() $B"\in W$
. Also,
$B"\in W$
. Also,
![]() $B"\subseteq B_0$
by clause
$B"\subseteq B_0$
by clause
![]() $(1)$
.
$(1)$
.
We proceed by a density argument, recalling that by the definition of
![]() $G_2$
, we have that
$G_2$
, we have that
![]() ${\langle } t_{<\kappa },t_\kappa {\rangle }\in G_\kappa *F_\kappa $
.
${\langle } t_{<\kappa },t_\kappa {\rangle }\in G_\kappa *F_\kappa $
.
Claim 2.17. Let D be the set of all conditions
![]() $q\in \mathcal {P}_{\kappa +1}$
, such that exists
$q\in \mathcal {P}_{\kappa +1}$
, such that exists
![]() $(\nu ^{\prime }_0,\nu _0),(\nu ^{\prime }_1,\nu _1)\in B', \ \nu ^{\prime }_1>\nu _0$
and a
$(\nu ^{\prime }_0,\nu _0),(\nu ^{\prime }_1,\nu _1)\in B', \ \nu ^{\prime }_1>\nu _0$
and a
![]() $\mathcal {P}_{\nu _0}$
-name
$\mathcal {P}_{\nu _0}$
-name
![]() such that:
such that:
-
(a)
 $r(\nu ^{\prime }_0,\nu _0),r(\nu ^{\prime }_1,\nu _1)\leq q$
.
$r(\nu ^{\prime }_0,\nu _0),r(\nu ^{\prime }_1,\nu _1)\leq q$
. -
(b)
 .
. -
(c)

Then D is dense (open) above
![]() ${\langle } t_{<\kappa },t_\kappa {\rangle }$
and thus
${\langle } t_{<\kappa },t_\kappa {\rangle }$
and thus
![]() $D\cap G_\kappa *F_\kappa \neq \emptyset .$
$D\cap G_\kappa *F_\kappa \neq \emptyset .$
Proof Work in V, and let
![]() ${\langle } t_{<\kappa },t_\kappa {\rangle }\leq p:={\langle } p_{<\kappa },p_\kappa {\rangle } \in {\mathcal P}_{\kappa +1}$
. We will define two extensions
${\langle } t_{<\kappa },t_\kappa {\rangle }\leq p:={\langle } p_{<\kappa },p_\kappa {\rangle } \in {\mathcal P}_{\kappa +1}$
. We will define two extensions
![]() $p\leq q\leq q^*$
which corresponds to the choice of
$p\leq q\leq q^*$
which corresponds to the choice of
![]() $(\nu ^{\prime }_0,\nu _0),(\nu ^{\prime }_1,\nu _1)$
such that
$(\nu ^{\prime }_0,\nu _0),(\nu ^{\prime }_1,\nu _1)$
such that
![]() $q^*\in D$
. By definition of
$q^*\in D$
. By definition of
![]() $\mathcal {P}_{\kappa +1}$
,
$\mathcal {P}_{\kappa +1}$
,
![]() $p_{<\kappa }\Vdash p_\kappa \in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
, by
$p_{<\kappa }\Vdash p_\kappa \in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
, by
![]() $\kappa -$
cc of
$\kappa -$
cc of
![]() $\mathcal {P}_\kappa $
, for some
$\mathcal {P}_\kappa $
, for some
![]() $Z\subseteq \kappa ^+,\ Z\in V$
,
$Z\subseteq \kappa ^+,\ Z\in V$
,
![]() $|Z|<\kappa $
and some
$|Z|<\kappa $
and some
![]() $\gamma <\kappa $
,
$\gamma <\kappa $
,
![]() $p_{<\kappa }\Vdash \operatorname {\mathrm {dom}}(p_\kappa )\subseteq \gamma \times Z$
. Applying
$p_{<\kappa }\Vdash \operatorname {\mathrm {dom}}(p_\kappa )\subseteq \gamma \times Z$
. Applying
![]() $j_2$
, we have that
$j_2$
, we have that
Combining with
![]() $(2c)$
, we have both
$(2c)$
, we have both
To reflect this, denote
![]() $\mu =(j_2\restriction (Z\cup \theta ))^{-1}\in M_2$
, then
$\mu =(j_2\restriction (Z\cup \theta ))^{-1}\in M_2$
, then
and we can reformulate
Also, since we can find
![]() $\delta <\kappa $
such that
$\delta <\kappa $
such that
![]() $t_{<\kappa }\Vdash \phi "(\delta ,\kappa )\cap Z=\emptyset .$
There exists such
$t_{<\kappa }\Vdash \phi "(\delta ,\kappa )\cap Z=\emptyset .$
There exists such
![]() $\delta $
since
$\delta $
since
![]() $|Z|<\kappa $
,
$|Z|<\kappa $
,
![]() $t_{<\kappa }\Vdash |\operatorname {\mathrm {Supp}}(t_{\kappa })|<\kappa $
and by
$t_{<\kappa }\Vdash |\operatorname {\mathrm {Supp}}(t_{\kappa })|<\kappa $
and by
![]() $\kappa $
-cc of
$\kappa $
-cc of
![]() $\mathcal {P}_\kappa $
. Recall that by the definition of
$\mathcal {P}_\kappa $
. Recall that by the definition of
![]() $\mu _1$
,
$\mu _1$
,
![]() $\phi "(\delta ,\kappa )=\mu _1^{\prime \prime }\{s_\gamma (\kappa _1)\mid \gamma \in j_2(\phi )"(\delta ,\kappa )\}$
and that
$\phi "(\delta ,\kappa )=\mu _1^{\prime \prime }\{s_\gamma (\kappa _1)\mid \gamma \in j_2(\phi )"(\delta ,\kappa )\}$
and that
![]() $\mu "\operatorname {\mathrm {Supp}}(j_2(p_\kappa ))=Z$
. Therefore in
$\mu "\operatorname {\mathrm {Supp}}(j_2(p_\kappa ))=Z$
. Therefore in
![]() $M_2$
we will have that
$M_2$
we will have that
Let
![]() $\Gamma $
be such that
$\Gamma $
be such that
![]() $j_2(\Gamma )(\kappa ,\kappa _1)=\mu $
, and there is a set
$j_2(\Gamma )(\kappa ,\kappa _1)=\mu $
, and there is a set
![]() $\overline {B}_0\subseteq B'$
,
$\overline {B}_0\subseteq B'$
,
![]() $\overline {B}_0\in U^2$
such that for every
$\overline {B}_0\in U^2$
such that for every
![]() $(\nu ',\nu )\in \overline {B}_0$
,
$(\nu ',\nu )\in \overline {B}_0$
,
Let us move to the choice of
![]() $(\nu ^{\prime }_0,\nu _0),(\nu ^{\prime }_1,\nu _1)$
. In
$(\nu ^{\prime }_0,\nu _0),(\nu ^{\prime }_1,\nu _1)$
. In
![]() $V[G_{\kappa }*F_{\kappa }]$
, there exists
$V[G_{\kappa }*F_{\kappa }]$
, there exists
![]() $(\nu ^0_0,\nu _0),(\nu ^0_1,\nu _1)\in \overline {B}_0$
such that
$(\nu ^0_0,\nu _0),(\nu ^0_1,\nu _1)\in \overline {B}_0$
such that
![]() $r(\nu ^0_0,\nu _0),r(\nu ^0_1,\nu _1)\in G_{\kappa }*F_{\kappa }$
(hence they are compatible) such that
$r(\nu ^0_0,\nu _0),r(\nu ^0_1,\nu _1)\in G_{\kappa }*F_{\kappa }$
(hence they are compatible) such that
![]() $\nu ^0_0>\delta ,\gamma ,\sup (\operatorname {\mathrm {Supp}}(p_{<\kappa }))$
and
$\nu ^0_0>\delta ,\gamma ,\sup (\operatorname {\mathrm {Supp}}(p_{<\kappa }))$
and
![]() $\nu ^0_1>\nu _0,\operatorname {\mathrm {Supp}}(r_{<\kappa }(\nu ^0_0,\nu _0))$
. In particular, in V we can find
$\nu ^0_1>\nu _0,\operatorname {\mathrm {Supp}}(r_{<\kappa }(\nu ^0_0,\nu _0))$
. In particular, in V we can find
![]() $(\nu ^{\prime }_0,\nu _0),(\nu ^{\prime }_1,\nu _1)\in \overline {B}_0$
such that
$(\nu ^{\prime }_0,\nu _0),(\nu ^{\prime }_1,\nu _1)\in \overline {B}_0$
such that
![]() $r(\nu _0^{\prime },\nu _0),r(\nu _1^{\prime },\nu _1)$
are compatible,
$r(\nu _0^{\prime },\nu _0),r(\nu _1^{\prime },\nu _1)$
are compatible,
![]() $\nu ^{\prime }_0>\delta ,\gamma ,\sup (\operatorname {\mathrm {Supp}}(p_{<\kappa }))$
, and
$\nu ^{\prime }_0>\delta ,\gamma ,\sup (\operatorname {\mathrm {Supp}}(p_{<\kappa }))$
, and
![]() $\nu ^{\prime }_1>\nu _0,\sup (\operatorname {\mathrm {Supp}}(r_{<\kappa }(\nu _0^{\prime },\nu _0)))$
. Denote
$\nu ^{\prime }_1>\nu _0,\sup (\operatorname {\mathrm {Supp}}(r_{<\kappa }(\nu _0^{\prime },\nu _0)))$
. Denote
Let us define the first extension q, and it has the form:
First,
![]() $q_{\nu ^{\prime }_0}$
is a
$q_{\nu ^{\prime }_0}$
is a
![]() $\mathcal {P}_{\nu ^{\prime }_0}$
-name for a condition with
$\mathcal {P}_{\nu ^{\prime }_0}$
-name for a condition with
![]() $\operatorname {\mathrm {Supp}}(q_{\nu ^{\prime }_0})= \Gamma (\nu ^{\prime }_0,\nu _0)"Z$
, by
$\operatorname {\mathrm {Supp}}(q_{\nu ^{\prime }_0})= \Gamma (\nu ^{\prime }_0,\nu _0)"Z$
, by
![]() $(i) \ \operatorname {\mathrm {Supp}}(q_{\nu ^{\prime }_0})\supseteq \operatorname {\mathrm {Supp}}(r^0_{\nu ^{\prime }_0})$
. Set
$(i) \ \operatorname {\mathrm {Supp}}(q_{\nu ^{\prime }_0})\supseteq \operatorname {\mathrm {Supp}}(r^0_{\nu ^{\prime }_0})$
. Set
![]() $q_{\nu ^{\prime }_0,\Gamma (\nu ^{\prime }_0,\nu _0)(\beta )}= p_{\kappa ,\beta }$
. As for
$q_{\nu ^{\prime }_0,\Gamma (\nu ^{\prime }_0,\nu _0)(\beta )}= p_{\kappa ,\beta }$
. As for
![]() $q_\kappa $
, we set it to be a
$q_\kappa $
, we set it to be a
![]() $\mathcal {P}_\kappa $
-name for
$\mathcal {P}_\kappa $
-name for
![]() $r^0_\kappa \cup p_\kappa $
.
$r^0_\kappa \cup p_\kappa $
.
Once we will prove that
![]() $p_{<\kappa },r^0_{<\kappa }\leq q_{<\kappa }$
, from
$p_{<\kappa },r^0_{<\kappa }\leq q_{<\kappa }$
, from
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
it will follow that
$(ii)$
it will follow that
![]() $q_{<\kappa }$
forces
$q_{<\kappa }$
forces
![]() $q_\kappa $
to be a partial function. Indeed, for every
$q_\kappa $
to be a partial function. Indeed, for every
![]() $\beta \in \operatorname {\mathrm {Supp}}(r^0_\kappa )\cap Z$
,
$\beta \in \operatorname {\mathrm {Supp}}(r^0_\kappa )\cap Z$
,
![]() $q_{<\kappa }$
will force
$q_{<\kappa }$
will force
Clearly
![]() $p\leq q$
. To see that
$p\leq q$
. To see that
![]() $r^0\leq q$
, up to
$r^0\leq q$
, up to
![]() $\nu ^{\prime }_0$
, we have that by
$\nu ^{\prime }_0$
, we have that by
![]() $(4)_{(\nu ^{\prime }_0,\nu _0)}$
that
$(4)_{(\nu ^{\prime }_0,\nu _0)}$
that
At
![]() $\nu ^{\prime }_0$
, if
$\nu ^{\prime }_0$
, if
![]() $\alpha = \Gamma (\nu ^{\prime }_0,\nu _0)(\beta )$
, then
$\alpha = \Gamma (\nu ^{\prime }_0,\nu _0)(\beta )$
, then
![]() $(i)$
insures that
$(i)$
insures that
![]() $q_{\nu ^{\prime }_0,\alpha }=p_{\kappa ,\beta }\geq r^0_{\nu ',\alpha }$
. Since in the interval
$q_{\nu ^{\prime }_0,\alpha }=p_{\kappa ,\beta }\geq r^0_{\nu ',\alpha }$
. Since in the interval
![]() $(\nu ^{\prime }_0,\kappa )$
, q and
$(\nu ^{\prime }_0,\kappa )$
, q and
![]() $r^0$
are the same, it follows that
$r^0$
are the same, it follows that
![]() $q_{<\kappa }\geq r^0_{<\kappa }$
and at
$q_{<\kappa }\geq r^0_{<\kappa }$
and at
![]() $\kappa $
it is clear that
$\kappa $
it is clear that
![]() $q_{<\kappa }\Vdash r^0_\kappa \leq q_\kappa $
.
$q_{<\kappa }\Vdash r^0_\kappa \leq q_\kappa $
.
Next let us move to the choice of
![]() . Since
. Since
![]() $r^0\leq q$
and
$r^0\leq q$
and
![]() , use the maximality principal to find a
, use the maximality principal to find a
![]() $\mathcal {P}_{\nu _0}$
-name,
$\mathcal {P}_{\nu _0}$
-name,
![]() such that q forces
such that q forces
![]() $(b)$
.Footnote
5
$(b)$
.Footnote
5
Define the final condition
![]() $q\leq q^*$
,
$q\leq q^*$
,
The crucial point here is that by
![]() $(2b)_{(\nu ^{\prime }_1,\nu _1)}$
,
$(2b)_{(\nu ^{\prime }_1,\nu _1)}$
,
and since
we have that
![]() $r^0\Vdash X_1^{\nu _0}\subseteq \phi "(\nu ^{\prime }_0,\nu _0)\subseteq \phi "(\nu ^{\prime }_0,\nu _1^{\prime })$
. By
$r^0\Vdash X_1^{\nu _0}\subseteq \phi "(\nu ^{\prime }_0,\nu _0)\subseteq \phi "(\nu ^{\prime }_0,\nu _1^{\prime })$
. By
![]() $(iii)$
we have that
$(iii)$
we have that
![]() $q_{<\kappa }\Vdash [\Gamma _1(\nu ^{\prime }_1,\nu _1)"\{s_\gamma (\nu _1)\mid \gamma \in X^{\nu _0}_1\}]\cap [\Gamma (\nu _1^{\prime },\nu _1)"Z]=\emptyset $
. This will permit to code
$q_{<\kappa }\Vdash [\Gamma _1(\nu ^{\prime }_1,\nu _1)"\{s_\gamma (\nu _1)\mid \gamma \in X^{\nu _0}_1\}]\cap [\Gamma (\nu _1^{\prime },\nu _1)"Z]=\emptyset $
. This will permit to code
![]() $d^{\nu _0}$
, let
$d^{\nu _0}$
, let
and

and
![]() $q^*_\kappa =q_\kappa \cup r^1_\kappa $
. Note that if
$q^*_\kappa =q_\kappa \cup r^1_\kappa $
. Note that if
![]() $\tau \in \operatorname {\mathrm {Supp}}(q_{\kappa })\cap \operatorname {\mathrm {Supp}}(r^1_{\kappa })$
then either
$\tau \in \operatorname {\mathrm {Supp}}(q_{\kappa })\cap \operatorname {\mathrm {Supp}}(r^1_{\kappa })$
then either
![]() $\tau \in \operatorname {\mathrm {Supp}}(r^0_{\kappa })\cap \operatorname {\mathrm {Supp}}(r^1_{\kappa })$
, and
$\tau \in \operatorname {\mathrm {Supp}}(r^0_{\kappa })\cap \operatorname {\mathrm {Supp}}(r^1_{\kappa })$
, and
![]() $r^0_{\kappa },r^1_{\kappa }$
are forced to be compatible by
$r^0_{\kappa },r^1_{\kappa }$
are forced to be compatible by
![]() $q_{<\kappa }$
and if
$q_{<\kappa }$
and if
![]() $\tau \in Z\cap \operatorname {\mathrm {Supp}}(r^1_{\kappa })$
then the same argument as before works. We conclude that
$\tau \in Z\cap \operatorname {\mathrm {Supp}}(r^1_{\kappa })$
then the same argument as before works. We conclude that
![]() $r^0\leq q\leq q^*$
,
$r^0\leq q\leq q^*$
,
![]() $r^1\leq q^*$
, namely
$r^1\leq q^*$
, namely
![]() $(a)$
. Finally, for every
$(a)$
. Finally, for every
![]() $\tau \in X^{\nu _0}_1$
,
$\tau \in X^{\nu _0}_1$
,
![]() $s_\tau (\nu _1)\in \operatorname {\mathrm {dom}}(\Gamma _1(\nu ^{\prime }_1,\nu _1))$
and by
$s_\tau (\nu _1)\in \operatorname {\mathrm {dom}}(\Gamma _1(\nu ^{\prime }_1,\nu _1))$
and by
![]() $(3)_{(\nu ^{\prime }_1,\nu _1)}$
we have that
$(3)_{(\nu ^{\prime }_1,\nu _1)}$
we have that
![]() $q^*$
forces that
$q^*$
forces that
Then
![]() $p\leq q^*$
and
$p\leq q^*$
and
![]() $q^*\in D.$
$q^*\in D.$
By density, we can find such a condition
![]() $p^*\in G_\kappa *F_\kappa \cap D$
and points
$p^*\in G_\kappa *F_\kappa \cap D$
and points
![]() $(\nu ^{\prime }_0,\nu _0),(\nu _1^{\prime },\nu _1)\in B'$
witnessing
$(\nu ^{\prime }_0,\nu _0),(\nu _1^{\prime },\nu _1)\in B'$
witnessing
![]() $p^*\in D$
. It follows that
$p^*\in D$
. It follows that
![]() $r(\nu ^{\prime }_0,\nu _0),r(\nu ^{\prime }_1,\nu _1)\in G_\kappa *F_\kappa $
, and by
$r(\nu ^{\prime }_0,\nu _0),r(\nu ^{\prime }_1,\nu _1)\in G_\kappa *F_\kappa $
, and by
![]() $(1)_{(\nu ^{\prime }_0,\nu _0)},(1)_{(\nu ^{\prime }_1,\nu _1)}$
,
$(1)_{(\nu ^{\prime }_0,\nu _0)},(1)_{(\nu ^{\prime }_1,\nu _1)}$
,
![]() $\nu _0,\nu _1\in B_0$
. Extend
$\nu _0,\nu _1\in B_0$
. Extend
![]() ${\langle } {\langle }{\rangle },B{\rangle }$
by
${\langle } {\langle }{\rangle },B{\rangle }$
by
![]() $p^*={\langle } \nu _0,\nu _1,B_0\cap (\cap _{\tau \in \phi "\nu _0}A_\tau {\rangle }\setminus \nu _1+1{\rangle }$
. By
$p^*={\langle } \nu _0,\nu _1,B_0\cap (\cap _{\tau \in \phi "\nu _0}A_\tau {\rangle }\setminus \nu _1+1{\rangle }$
. By
![]() $(2b)_{(\nu ^{\prime }_1,\nu _1)}$
, for every
$(2b)_{(\nu ^{\prime }_1,\nu _1)}$
, for every
![]() $\tau \in \phi "\nu _0\subseteq \phi "\nu ^{\prime }_1$
,
$\tau \in \phi "\nu _0\subseteq \phi "\nu ^{\prime }_1$
,
![]() $f_{\kappa ,\tau }(\nu _1)=r_{\kappa ,\tau }(\nu _1)=1$
, hence
$f_{\kappa ,\tau }(\nu _1)=r_{\kappa ,\tau }(\nu _1)=1$
, hence
![]() $\nu _1\in \cap _{\tau \in \phi "\nu _0}A_\tau $
and
$\nu _1\in \cap _{\tau \in \phi "\nu _0}A_\tau $
and
 $p^*\Vdash n_\tau =\begin {cases} 0, &\tau \in X_0,\\ 1, & \tau \in X_1.\end {cases}$
In other words, since
$p^*\Vdash n_\tau =\begin {cases} 0, &\tau \in X_0,\\ 1, & \tau \in X_1.\end {cases}$
In other words, since
![]() $\nu _0\in B_0$
,
$\nu _0\in B_0$
,
Let
, it follows that
extends
![]() $d_\tau $
, and by
$d_\tau $
, and by
![]() $(c)$
of the definition of D,
$(c)$
of the definition of D,
extends
![]() $d_\tau $
. Thus
$d_\tau $
. Thus
. This concludes the genericity proof.
⊣
3 The results where
 $2^{\kappa }=\kappa ^{++}$
$2^{\kappa }=\kappa ^{++}$
3.1 Strong non-Galvin witnesses of length
 $2^{\kappa }=\kappa ^{++}$
$2^{\kappa }=\kappa ^{++}$
In this section we produce a model with a non-Galvin ultrafilter with a strong witnessing sequence of length
![]() $2^{\kappa }=\kappa ^{++}$
. This will of course require to violate GCH on a measurable cardinal and in turn to start with a stronger large cardinal assumption (see [Reference Gitik15, Reference Mitchell32]). We will follow a similar construction to the one given in the case of
$2^{\kappa }=\kappa ^{++}$
. This will of course require to violate GCH on a measurable cardinal and in turn to start with a stronger large cardinal assumption (see [Reference Gitik15, Reference Mitchell32]). We will follow a similar construction to the one given in the case of
![]() $\kappa ^+$
addressed in previous sections. Indeed, instead of iterating
$\kappa ^+$
addressed in previous sections. Indeed, instead of iterating
![]() $\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)$
we will iterate
$\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^+)$
we will iterate
![]() $\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^{++})$
aiming to force
$\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^{++})$
aiming to force
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})$
, from which we will be able to define a non-Galvin ultrafilter and a strong witness of length
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})$
, from which we will be able to define a non-Galvin ultrafilter and a strong witness of length
![]() $\kappa ^{++}$
in a similar fashion to the one we have on
$\kappa ^{++}$
in a similar fashion to the one we have on
![]() $\kappa ^+$
, distinguishing between
$\kappa ^+$
, distinguishing between
![]() $\alpha $
’s which are in the image of the second iteration and those which are in the image of the factor map. The difficulty is, as always, to extend a ground model embedding. By the large cardinal lower bound, we can no longer work with an ultrapower by an ultrafilter. The usual embedding to lift in the context of violation of GCH at measurables is a
$\alpha $
’s which are in the image of the second iteration and those which are in the image of the factor map. The difficulty is, as always, to extend a ground model embedding. By the large cardinal lower bound, we can no longer work with an ultrapower by an ultrafilter. The usual embedding to lift in the context of violation of GCH at measurables is a
![]() $(\kappa ,\kappa ^{++})$
-extender ultrapower embedding, which we will use here. This makes the lifting argument more involved and the existence of generic filters for the iteration requires variations of Woodin’s surgery method (see [Reference Cummings, Foreman and Kanamori12, Section 25]).
$(\kappa ,\kappa ^{++})$
-extender ultrapower embedding, which we will use here. This makes the lifting argument more involved and the existence of generic filters for the iteration requires variations of Woodin’s surgery method (see [Reference Cummings, Foreman and Kanamori12, Section 25]).
Theorem 3.1. Assume GCH and that there is a
![]() $(\kappa ,\kappa ^{++})$
-extender over
$(\kappa ,\kappa ^{++})$
-extender over
![]() $\kappa $
in V. Then there is a cofinality preserving forcing extension
$\kappa $
in V. Then there is a cofinality preserving forcing extension
![]() $V^*$
such that
$V^*$
such that
![]() $V^*\models 2^{\kappa }=\kappa ^{++}$
, and in
$V^*\models 2^{\kappa }=\kappa ^{++}$
, and in
![]() $V^*$
there is a
$V^*$
there is a
![]() $\kappa $
-complete ultrafilter W over
$\kappa $
-complete ultrafilter W over
![]() $\kappa $
which concentrates on regulars, extends
$\kappa $
which concentrates on regulars, extends
![]() $Cub_\kappa $
, and has a strong witness of length
$Cub_\kappa $
, and has a strong witness of length
![]() $\kappa ^{++}$
for the failure of Galvin’s property.
$\kappa ^{++}$
for the failure of Galvin’s property.
Proof Let E be a
![]() $(\kappa ,\kappa ^{++})$
-extender. Let
$(\kappa ,\kappa ^{++})$
-extender. Let
![]() $j_1=j_E:V\to M_E=:M_1$
be its ultrapower embedding with
$j_1=j_E:V\to M_E=:M_1$
be its ultrapower embedding with
![]() $crit(j_E)=\kappa $
and
$crit(j_E)=\kappa $
and
![]() ${}^{\kappa } M_E\subseteq M_E$
. Denote by
${}^{\kappa } M_E\subseteq M_E$
. Denote by
![]() $E_\alpha $
the ultrafilter
$E_\alpha $
the ultrafilter
Denote
![]() $U:=E_\kappa $
the normal ultrafilter and let
$U:=E_\kappa $
the normal ultrafilter and let
![]() $k:M_U \to M_E$
be the factor map defined by setting
$k:M_U \to M_E$
be the factor map defined by setting
![]() $k(j_U(f)(\kappa ))=j_E(f)(\kappa )$
such that
$k(j_U(f)(\kappa ))=j_E(f)(\kappa )$
such that
![]() $j_E=k\circ j_U$
. Define an Easton support iteration
$j_E=k\circ j_U$
. Define an Easton support iteration
![]() as follows:
as follows:
![]() is trivial unless
is trivial unless
![]() $\beta $
is inaccessible, in which case
$\beta $
is inaccessible, in which case
![]() $Q_{\beta }=\operatorname {\mathrm {Cohen}}(\beta , \beta ^{++})$
.
$Q_{\beta }=\operatorname {\mathrm {Cohen}}(\beta , \beta ^{++})$
.
Let
![]() $G_{\kappa +1}:=G_\kappa *g_\kappa $
be a V-generic subset of
$G_{\kappa +1}:=G_\kappa *g_\kappa $
be a V-generic subset of
![]() . Keeping similar notations to those from previous sections, let
. Keeping similar notations to those from previous sections, let
![]() ${\langle } f_{\kappa ,\alpha } \mid \alpha <\kappa ^{++}{\rangle } $
be the Cohen generic functions from
${\langle } f_{\kappa ,\alpha } \mid \alpha <\kappa ^{++}{\rangle } $
be the Cohen generic functions from
![]() $\kappa $
to
$\kappa $
to
![]() $2$
introduced by
$2$
introduced by
![]() $g_\kappa $
.
$g_\kappa $
.
Now we apply Woodin’s argument (see [Reference Cummings, Foreman and Kanamori12, Section 25], and [Reference Ben-Shalom10] for constructing generics without additional forcing) to see that there will be
![]() $G_{j_E(\kappa )+1}*H^*\subseteq j_E({\mathcal P}_{\kappa +1})*\mathbb {S}_0$
in
$G_{j_E(\kappa )+1}*H^*\subseteq j_E({\mathcal P}_{\kappa +1})*\mathbb {S}_0$
in
![]() $V^*_1:=V[G_{\kappa +1}][H]$
, where
$V^*_1:=V[G_{\kappa +1}][H]$
, where
![]() $H\subseteq \mathbb {S}_0$
is a
$H\subseteq \mathbb {S}_0$
is a
![]() $V[G_{\kappa +1}]$
-generic filter, where
$V[G_{\kappa +1}]$
-generic filter, where
![]() $\mathbb {S}_0$
is some
$\mathbb {S}_0$
is some
![]() $\kappa ^+$
-distributive in
$\kappa ^+$
-distributive in
![]() $V[G_{\kappa +1}]$
(in the case of Ben-Shalom, there is no need for
$V[G_{\kappa +1}]$
(in the case of Ben-Shalom, there is no need for
![]() $H^*$
and we can work directly in
$H^*$
and we can work directly in
![]() $V[G_{\kappa +1}]$
) generic over
$V[G_{\kappa +1}]$
) generic over
![]() $M_E$
and an elementary embedding
$M_E$
and an elementary embedding
which extends
![]() $j_1$
. Recall that the generic filter constructed for
$j_1$
. Recall that the generic filter constructed for
![]() $j_1(Q_\kappa )$
is obtained by a surgery argument, making small changes on an
$j_1(Q_\kappa )$
is obtained by a surgery argument, making small changes on an
![]() $M_1[G_{j_1(\kappa )}]$
-generic filter f to be compatible with
$M_1[G_{j_1(\kappa )}]$
-generic filter f to be compatible with
![]() $j^{\prime \prime }_1g_\kappa $
. For our purposes, we need some additional changes to be made; for every
$j^{\prime \prime }_1g_\kappa $
. For our purposes, we need some additional changes to be made; for every
![]() $p\in f$
we change p to
$p\in f$
we change p to
![]() $p^*$
such that
$p^*$
such that
![]() $\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and
$\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and
 $$ \begin{align*}p^*({\langle}\gamma,\alpha{\rangle})=\begin{cases}f_\beta(\gamma), & \gamma<\kappa \wedge \alpha=j_1(\beta),\\ \beta, & \gamma=\kappa\wedge \alpha=j_1(\beta),\\ p({\langle}\gamma,\alpha{\rangle}), & \text{else}.\end{cases}\end{align*} $$
$$ \begin{align*}p^*({\langle}\gamma,\alpha{\rangle})=\begin{cases}f_\beta(\gamma), & \gamma<\kappa \wedge \alpha=j_1(\beta),\\ \beta, & \gamma=\kappa\wedge \alpha=j_1(\beta),\\ p({\langle}\gamma,\alpha{\rangle}), & \text{else}.\end{cases}\end{align*} $$
To see that p was only changed at
![]() $\kappa $
-many places, find
$\kappa $
-many places, find
![]() $a\in [\kappa ^{++}]^{<\omega }$
such that
$a\in [\kappa ^{++}]^{<\omega }$
such that
![]() $j_E(P)(a)=p$
, where
$j_E(P)(a)=p$
, where
![]() $P:\kappa ^{|a|}\rightarrow Q_\kappa $
. By elementarity, for every
$P:\kappa ^{|a|}\rightarrow Q_\kappa $
. By elementarity, for every
![]() ${\langle } \alpha ,j_1(\beta ){\rangle }\in \kappa \times j_1^{\prime \prime }\kappa ^{++}\cap \operatorname {\mathrm {dom}}(p)$
, there is
${\langle } \alpha ,j_1(\beta ){\rangle }\in \kappa \times j_1^{\prime \prime }\kappa ^{++}\cap \operatorname {\mathrm {dom}}(p)$
, there is
![]() $x\in [\kappa ]^{|a|}$
such that
$x\in [\kappa ]^{|a|}$
such that
![]() ${\langle }\alpha ,\beta {\rangle }\in \operatorname {\mathrm {dom}}(P(x))$
. It follows that
${\langle }\alpha ,\beta {\rangle }\in \operatorname {\mathrm {dom}}(P(x))$
. It follows that
![]() $|\kappa \times j_1^{\prime \prime }\kappa ^{++}\cap \operatorname {\mathrm {dom}}(p)|\leq \kappa $
. Moreover,
$|\kappa \times j_1^{\prime \prime }\kappa ^{++}\cap \operatorname {\mathrm {dom}}(p)|\leq \kappa $
. Moreover,
![]() $|\{\kappa \}\times j^{\prime \prime }_1\kappa ^{++}\cap \operatorname {\mathrm {dom}}(p)|\leq \kappa $
, since otherwise there would be some
$|\{\kappa \}\times j^{\prime \prime }_1\kappa ^{++}\cap \operatorname {\mathrm {dom}}(p)|\leq \kappa $
, since otherwise there would be some
![]() $\alpha <\kappa ^{++}$
such that
$\alpha <\kappa ^{++}$
such that
But
![]() $|\operatorname {\mathrm {dom}}(p)|^{M_1}<j_1(\kappa )$
and
$|\operatorname {\mathrm {dom}}(p)|^{M_1}<j_1(\kappa )$
and
![]() ${\mathrm {cf}}^{M_1}(j_1(\alpha ))=j_1(\kappa )^+$
which is a contradiction. Hence
${\mathrm {cf}}^{M_1}(j_1(\alpha ))=j_1(\kappa )^+$
which is a contradiction. Hence
![]() $p^*\in M_1[G_{j_1(\kappa )}]$
since we have only changed p at
$p^*\in M_1[G_{j_1(\kappa )}]$
since we have only changed p at
![]() $\kappa $
-many values and
$\kappa $
-many values and
![]() ${}^{\kappa } M_1[G_{j_1(\kappa )}]\subseteq M_1[G_{j_1(\kappa )}]$
.
${}^{\kappa } M_1[G_{j_1(\kappa )}]\subseteq M_1[G_{j_1(\kappa )}]$
.
The argument that such changes do not affect the genericity is the same as in [Reference Cummings, Foreman and Kanamori12]. So we additionally obtain that
![]() $f_{\kappa _1,j_1(\beta )}(\kappa )=\beta ,$
for every
$f_{\kappa _1,j_1(\beta )}(\kappa )=\beta ,$
for every
![]() $\beta <\kappa ^{++}$
.
$\beta <\kappa ^{++}$
.
We also claim that
![]() $j^*_1$
is actually the ultrapower embedding by the normal ultrafilter
$j^*_1$
is actually the ultrapower embedding by the normal ultrafilter
extending U. To see this, consider
![]() $k^*:M_{U^*}\rightarrow M_1[G_{j_1(\kappa )+1}*H^*]$
defined by
$k^*:M_{U^*}\rightarrow M_1[G_{j_1(\kappa )+1}*H^*]$
defined by
![]() $k^*([f]_{U^*})=j^*_1(f)(\kappa )$
, which is clearly elementary. To see that
$k^*([f]_{U^*})=j^*_1(f)(\kappa )$
, which is clearly elementary. To see that
![]() $k^*=id$
, let us prove that
$k^*=id$
, let us prove that
![]() $k^*$
is onto. Fix
$k^*$
is onto. Fix
and let
![]() $f\in V$
,
$f\in V$
,
![]() $a=\{\alpha _1,...,\alpha _r\}\in [\kappa ^{++}]^{<\omega }$
be such that
$a=\{\alpha _1,...,\alpha _r\}\in [\kappa ^{++}]^{<\omega }$
be such that
. Define in
![]() $V[G_{\kappa +1}]$
the function
$V[G_{\kappa +1}]$
the function
![]() $f^*(x)=(f(\{f_{\alpha _1}(x),...,f_{\alpha _r}(x)\}))_{G_{\kappa +1}*H}$
. Then
$f^*(x)=(f(\{f_{\alpha _1}(x),...,f_{\alpha _r}(x)\}))_{G_{\kappa +1}*H}$
. Then
We would like now to construct a
![]() $\kappa $
-complete ultrafilter
$\kappa $
-complete ultrafilter
![]() $W\in V[G_{\kappa +1}]$
over
$W\in V[G_{\kappa +1}]$
over
![]() $\kappa $
which includes
$\kappa $
which includes
![]() $Cub_\kappa $
and the family
$Cub_\kappa $
and the family
![]() ${\langle } A_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
which is a strong witness that W fails to satisfy the Galvin Property. Set
${\langle } A_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
which is a strong witness that W fails to satisfy the Galvin Property. Set
for every
![]() $\alpha <\kappa ^{++}$
.
$\alpha <\kappa ^{++}$
.
Consider the second ultrapower (of V) by E, i.e.,
![]() $\mathrm {Ult}(M_E, j_E(E))$
. In order to simplify the notation let us denote
$\mathrm {Ult}(M_E, j_E(E))$
. In order to simplify the notation let us denote
![]() $M_E$
by
$M_E$
by
![]() $M_1$
and
$M_1$
and
![]() $\mathrm {Ult}(M_1, j_1(E))$
by
$\mathrm {Ult}(M_1, j_1(E))$
by
![]() $M_2$
and
$M_2$
and
![]() $j_{2,1}:=j_{j_1(E)}:M_1\rightarrow M_2$
. Also, let
$j_{2,1}:=j_{j_1(E)}:M_1\rightarrow M_2$
. Also, let
![]() $\kappa _1=j_1(\kappa ), E_1=j_1(E),$
and
$\kappa _1=j_1(\kappa ), E_1=j_1(E),$
and
![]() $\kappa _2=j_{2,1}(\kappa _1)$
. Let
$\kappa _2=j_{2,1}(\kappa _1)$
. Let
![]() $j_2:V\to M_2$
be the composition of
$j_2:V\to M_2$
be the composition of
![]() $j_1$
with
$j_1$
with
![]() $j_{2,1}$
.
$j_{2,1}$
.
Work in
![]() $M_1[G_{\kappa _1+1}*H^*]$
, and apply there the Woodin argument to
$M_1[G_{\kappa _1+1}*H^*]$
, and apply there the Woodin argument to
![]() $E_1$
. There will be
$E_1$
. There will be
![]() $G_{\kappa _2+1}*H^{**}\subseteq j_2(P_{\kappa }*Q_\kappa *\mathbb {S}_0)$
(in
$G_{\kappa _2+1}*H^{**}\subseteq j_2(P_{\kappa }*Q_\kappa *\mathbb {S}_0)$
(in
![]() $M_1[G_{\kappa _1+1}*H^*]$
) generic over
$M_1[G_{\kappa _1+1}*H^*]$
) generic over
![]() $M_2$
and an elementary embedding
$M_2$
and an elementary embedding
which extends
![]() $j_{E_1}$
. Additionally, for every
$j_{E_1}$
. Additionally, for every
![]() $\alpha <(\kappa _1^{++})^{M_1}$
let us arrange the following:
$\alpha <(\kappa _1^{++})^{M_1}$
let us arrange the following:
-
(1)
 $f_{\kappa _2,j_{2,1}(\alpha )}(\kappa _1)$
is odd, if
$f_{\kappa _2,j_{2,1}(\alpha )}(\kappa _1)$
is odd, if
 $\alpha \in j_E^{\prime \prime }\kappa ^{++}$
.
$\alpha \in j_E^{\prime \prime }\kappa ^{++}$
. -
(2)
 $f_{\kappa _2, j_{2,1}(\alpha )}(\kappa _1)$
is an even, if
$f_{\kappa _2, j_{2,1}(\alpha )}(\kappa _1)$
is an even, if
 $\alpha \in (\kappa _1^{++})^{M_1}\setminus j_E^{\prime \prime }\kappa ^{++}$
.
$\alpha \in (\kappa _1^{++})^{M_1}\setminus j_E^{\prime \prime }\kappa ^{++}$
. -
(3)
 $f_{\kappa _2,\kappa _1}(\kappa _1)=\kappa $
.
$f_{\kappa _2,\kappa _1}(\kappa _1)=\kappa $
.
The point being that this requires only small changes of conditions in
![]() $(\operatorname {\mathrm {Cohen}}(\kappa _2, \kappa _2^{++}))^{M_2}$
, and so preserves the genericity.
$(\operatorname {\mathrm {Cohen}}(\kappa _2, \kappa _2^{++}))^{M_2}$
, and so preserves the genericity.
Namely, given
![]() $p \in (\operatorname {\mathrm {Cohen}}(\kappa _2, (\kappa _2)^{++}))^{M_2}$
, define
$p \in (\operatorname {\mathrm {Cohen}}(\kappa _2, (\kappa _2)^{++}))^{M_2}$
, define
![]() $p^*$
such that
$p^*$
such that
![]() $\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and
$\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and
 $$ \begin{align*}p^*({\langle}\gamma,\alpha{\rangle})=\begin{cases} f_{\kappa_1,\beta}(\gamma), & \gamma<\kappa_1\wedge\exists \beta<\kappa_1^{++} \alpha=j_{2,1}(\beta),\\ \beta\cdot 2+1, & \gamma=\kappa_1\wedge \exists\beta\in j_1^{\prime\prime}\kappa^{++}.\alpha=j_{2,1}(\beta),\\ \beta\cdot 2, & \gamma=\kappa_1\wedge \exists\beta\in\kappa_1^{++}\setminus j_1^{\prime\prime}\kappa^{++}.j_{2,1}(\beta)=\alpha,\\ \kappa, & \gamma=\alpha=\kappa_1,\\ p({\langle}\gamma,\alpha{\rangle}), & \text{otherwise}.\end{cases}\end{align*} $$
$$ \begin{align*}p^*({\langle}\gamma,\alpha{\rangle})=\begin{cases} f_{\kappa_1,\beta}(\gamma), & \gamma<\kappa_1\wedge\exists \beta<\kappa_1^{++} \alpha=j_{2,1}(\beta),\\ \beta\cdot 2+1, & \gamma=\kappa_1\wedge \exists\beta\in j_1^{\prime\prime}\kappa^{++}.\alpha=j_{2,1}(\beta),\\ \beta\cdot 2, & \gamma=\kappa_1\wedge \exists\beta\in\kappa_1^{++}\setminus j_1^{\prime\prime}\kappa^{++}.j_{2,1}(\beta)=\alpha,\\ \kappa, & \gamma=\alpha=\kappa_1,\\ p({\langle}\gamma,\alpha{\rangle}), & \text{otherwise}.\end{cases}\end{align*} $$
In
![]() $V[G_{\kappa +1}*H]$
,
$V[G_{\kappa +1}*H]$
,
![]() $|\operatorname {\mathrm {Supp}}(p)\cap j_2^{*\prime \prime }\kappa ^{++}|\leq \kappa $
and
$|\operatorname {\mathrm {Supp}}(p)\cap j_2^{*\prime \prime }\kappa ^{++}|\leq \kappa $
and
![]() $M_1[G_{\kappa _1+1}*H^*]$
is closed under
$M_1[G_{\kappa _1+1}*H^*]$
is closed under
![]() $\kappa $
-sequences, hence
$\kappa $
-sequences, hence
![]() $p^*\in M_1$
. The argument we have seen before applied in
$p^*\in M_1$
. The argument we have seen before applied in
![]() $M_1[G_{\kappa _1+1}*H^{*}]$
shows that
$M_1[G_{\kappa _1+1}*H^{*}]$
shows that
This implies that
![]() $p^*\in M_2[G_{\kappa _2+1}*H^{**}]$
since
$p^*\in M_2[G_{\kappa _2+1}*H^{**}]$
since
![]() $M_2[G_{\kappa _2+1}*H^{**}]$
is closed under
$M_2[G_{\kappa _2+1}*H^{**}]$
is closed under
![]() $\kappa _1$
-sequences from
$\kappa _1$
-sequences from
![]() $M_1[G_{\kappa _1+1}*H^*]$
. Then the embedding
$M_1[G_{\kappa _1+1}*H^*]$
. Then the embedding
![]() $j_2:V\to M_2$
extends to
$j_2:V\to M_2$
extends to
Define now
Claim 3.2.
-
(1)
 $j_W=j^*_2$
,
$j_W=j^*_2$
,
 $[id]_W=\kappa _1$
,
$[id]_W=\kappa _1$
,
 $U^*\leq _{R-K}W$
.
$U^*\leq _{R-K}W$
. -
(2)
 $Cub_\kappa \subseteq W$
,
$Cub_\kappa \subseteq W$
,
 $\{\alpha <\kappa \mid {\mathrm {cf}}(\alpha )=\alpha )\}\in W$
.
$\{\alpha <\kappa \mid {\mathrm {cf}}(\alpha )=\alpha )\}\in W$
. -
(3) The sequence
 ${\langle } A_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
is a strong witness for
${\langle } A_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
is a strong witness for
 $\neg \text {Gal}(W,\kappa ,\kappa ^{++})$
, where
$\neg \text {Gal}(W,\kappa ,\kappa ^{++})$
, where  $$ \begin{align*}A_\alpha:=\{\nu<\kappa\mid f_{\kappa,\alpha}(\nu)\text{ is odd}\}.\end{align*} $$
$$ \begin{align*}A_\alpha:=\{\nu<\kappa\mid f_{\kappa,\alpha}(\nu)\text{ is odd}\}.\end{align*} $$
Proof Indeed
![]() $Cub_\kappa \subseteq W$
and
$Cub_\kappa \subseteq W$
and
![]() $\{\alpha <\kappa \mid {\mathrm {cf}}(\alpha )=\alpha \}\in W$
, is the same as in Claim 2.8 from the last section. To see
$\{\alpha <\kappa \mid {\mathrm {cf}}(\alpha )=\alpha \}\in W$
, is the same as in Claim 2.8 from the last section. To see
![]() $(1)$
, we let
$(1)$
, we let
![]() $k_W:M_W\rightarrow M_2[j_2^*(G)]$
be the usual factor map
$k_W:M_W\rightarrow M_2[j_2^*(G)]$
be the usual factor map
![]() $k_W([f]_W)=j^*_2(f)(\kappa _1)$
and we prove that
$k_W([f]_W)=j^*_2(f)(\kappa _1)$
and we prove that
![]() $k_W=id$
by proving that
$k_W=id$
by proving that
![]() $k_W$
is onto. Let
$k_W$
is onto. Let
![]() $A\in M_2[G_{\kappa _2+1}*H^{**}]$
, then
$A\in M_2[G_{\kappa _2+1}*H^{**}]$
, then
where
is a
![]() $\mathcal {P}_{\kappa _2+1}*j_2(\mathbb {S}_0)$
-name. Since
$\mathcal {P}_{\kappa _2+1}*j_2(\mathbb {S}_0)$
-name. Since
![]() $j_{2,1}$
is a
$j_{2,1}$
is a
![]() $(\kappa _1,\kappa _1^{++})$
-extender ultrapower, there is
$(\kappa _1,\kappa _1^{++})$
-extender ultrapower, there is
![]() $f\in M_1$
and
$f\in M_1$
and
![]() $a\in [\kappa _1^{++}]^{<\omega }$
such that
$a\in [\kappa _1^{++}]^{<\omega }$
such that
. Suppose that
![]() $a=\{\alpha _1,...,\alpha _n\}$
is an increasing enumeration. Then by construction,
$a=\{\alpha _1,...,\alpha _n\}$
is an increasing enumeration. Then by construction,
![]() $f_{\kappa _2,j_{2,1}(\alpha _i)}(\kappa _1)\in \{\alpha _i\cdot 2,\alpha _i\cdot 2+1\}$
. In particular we derive
$f_{\kappa _2,j_{2,1}(\alpha _i)}(\kappa _1)\in \{\alpha _i\cdot 2,\alpha _i\cdot 2+1\}$
. In particular we derive
![]() $\alpha _i$
from
$\alpha _i$
from
![]() $f_{\kappa _2,j_{2,1}(\alpha _i)}(\kappa _1)$
Footnote
6
. Define
$f_{\kappa _2,j_{2,1}(\alpha _i)}(\kappa _1)$
Footnote
6
. Define
![]() $g_{\alpha _i}:\kappa _1\rightarrow \kappa _1\in M_1[G_{\kappa _1+1}*H^*]$
by
$g_{\alpha _i}:\kappa _1\rightarrow \kappa _1\in M_1[G_{\kappa _1+1}*H^*]$
by
![]() $g_{\alpha _i}(\alpha )=\lfloor \frac {f_{\kappa _1,\alpha _i}(\alpha )}{2}\rfloor $
, then
$g_{\alpha _i}(\alpha )=\lfloor \frac {f_{\kappa _1,\alpha _i}(\alpha )}{2}\rfloor $
, then
![]() $j^*_{2,1}(g_{\alpha _i})(\kappa _1)=\lfloor \frac {f_{\kappa _2,j_{2,1}(\alpha _i)}(\kappa _1)}{2}\rfloor =\alpha _i$
. Finally, let
$j^*_{2,1}(g_{\alpha _i})(\kappa _1)=\lfloor \frac {f_{\kappa _2,j_{2,1}(\alpha _i)}(\kappa _1)}{2}\rfloor =\alpha _i$
. Finally, let
![]() $g(\alpha )=f(g_{\alpha _1}(\alpha ),...,g_{\alpha _n}(\alpha ))$
. Then,
$g(\alpha )=f(g_{\alpha _1}(\alpha ),...,g_{\alpha _n}(\alpha ))$
. Then,
We already know that
![]() $M_1[G_{\kappa _1+1}*H^*]$
is the ultrapower by
$M_1[G_{\kappa _1+1}*H^*]$
is the ultrapower by
![]() $U^*$
, hence
$U^*$
, hence
![]() $g=j^*_1(h)(\kappa )$
for some
$g=j^*_1(h)(\kappa )$
for some
![]() $h\in V[G_{\kappa +1}*H]$
and in turn
$h\in V[G_{\kappa +1}*H]$
and in turn
. Finally, we made sure that
![]() $\kappa $
is expressible by
$\kappa $
is expressible by
![]() $\kappa _1$
, so we define in
$\kappa _1$
, so we define in
![]() $V[G_{\kappa +1}*H] \ f^*:\kappa \rightarrow \kappa $
by
$V[G_{\kappa +1}*H] \ f^*:\kappa \rightarrow \kappa $
by
It follows that
this concludes
![]() $(1)$
.
$(1)$
.
![]() $(2)$
and
$(2)$
and
![]() $(3)$
are completely analogous to Claim 2.8.
$(3)$
are completely analogous to Claim 2.8.
3.2 Adding
 $\kappa ^{++}$
-Cohens using Prikry forcing
$\kappa ^{++}$
-Cohens using Prikry forcing
The construction of the previous section can be modified to obtain a model in which there is a
![]() $\kappa $
-complete ultrafilter
$\kappa $
-complete ultrafilter
![]() $U^*$
over
$U^*$
over
![]() $\kappa $
such that
$\kappa $
such that
![]() $\operatorname {\mathrm {Prikry}}(U^*)$
adds a generic filter for
$\operatorname {\mathrm {Prikry}}(U^*)$
adds a generic filter for
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})$
. This will require the violation of
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})$
. This will require the violation of
![]() $SCH$
and in turn larger cardinals [Reference Gitik16, Reference Mitchell33].
$SCH$
and in turn larger cardinals [Reference Gitik16, Reference Mitchell33].
Theorem 3.3. Assume
![]() $GCH$
and that E is a
$GCH$
and that E is a
![]() $(\kappa ,\kappa ^{++})$
-extender in V. Then there is a cofinality preserving forcing extension
$(\kappa ,\kappa ^{++})$
-extender in V. Then there is a cofinality preserving forcing extension
![]() $V^*$
in which
$V^*$
in which
![]() $2^{\kappa }=\kappa ^{++}$
and a non-Galvin ultrafilter
$2^{\kappa }=\kappa ^{++}$
and a non-Galvin ultrafilter
![]() $W\in V^*$
such that forcing with
$W\in V^*$
such that forcing with
![]() $\operatorname {\mathrm {Prikry}}(W)$
introduces a
$\operatorname {\mathrm {Prikry}}(W)$
introduces a
![]() $V^*$
-generic filter for
$V^*$
-generic filter for
![]() $Cohen^{V^*}(\kappa ,\kappa ^{++})$
-generic filter.
$Cohen^{V^*}(\kappa ,\kappa ^{++})$
-generic filter.
Proof Let
![]() $j_1:V\to M_E=:M_1$
be the ultrapower embedding of E with
$j_1:V\to M_E=:M_1$
be the ultrapower embedding of E with
![]() $crit(j_1)=\kappa $
and
$crit(j_1)=\kappa $
and
![]() ${}^{\kappa } M_1\subseteq M_1$
and
${}^{\kappa } M_1\subseteq M_1$
and
![]() $\kappa _1=j_1(\kappa )$
. Denote by
$\kappa _1=j_1(\kappa )$
. Denote by
![]() $E_\alpha $
the ultrafilter
$E_\alpha $
the ultrafilter
![]() $\{X\subseteq \kappa \mid \alpha \in j_E(X)\}$
. As before, denote
$\{X\subseteq \kappa \mid \alpha \in j_E(X)\}$
. As before, denote
![]() $E_\kappa $
by U and let
$E_\kappa $
by U and let
![]() $k:M_U \to M_E$
be defined by setting
$k:M_U \to M_E$
be defined by setting
![]() $k(j_U(f)(\kappa ))=j_E(f)(\kappa )$
. Define an Easton support iteration
$k(j_U(f)(\kappa ))=j_E(f)(\kappa )$
. Define an Easton support iteration
![]() as follows:
as follows:
is trivial unless
![]() $\beta $
is inaccessible. If
$\beta $
is inaccessible. If
![]() $\beta <\kappa $
is inaccessible, then
$\beta <\kappa $
is inaccessible, then
Over
![]() $\kappa $
, we let
$\kappa $
, we let
.
Let
![]() $G_{\kappa +1}=G_\kappa *F_\kappa $
be a V-generic filter of
$G_{\kappa +1}=G_\kappa *F_\kappa $
be a V-generic filter of
![]() ${\mathcal P}_{\kappa +1}$
. We denote by
${\mathcal P}_{\kappa +1}$
. We denote by
![]() $F_\alpha :={\langle } f_{\alpha , \gamma }\mid \gamma <\alpha ^{++}{\rangle }$
the generic Cohen function if
$F_\alpha :={\langle } f_{\alpha , \gamma }\mid \gamma <\alpha ^{++}{\rangle }$
the generic Cohen function if
![]() $\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^{++})$
was forced in
$\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^{++})$
was forced in
![]() $G_\kappa $
and by
$G_\kappa $
and by
if
![]() $\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^{++})\times \operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^{++})$
was. The elementary embedding
$\operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^{++})\times \operatorname {\mathrm {Cohen}}(\alpha ,\alpha ^{++})$
was. The elementary embedding
![]() $j_1$
extends to
$j_1$
extends to
![]() $j^*_1:V[G_{\kappa +1}]\to M_1[G_{\kappa _1+1}]$
such that at
$j^*_1:V[G_{\kappa +1}]\to M_1[G_{\kappa _1+1}]$
such that at
![]() $\kappa $
we forced one block of Cohen’s,
$\kappa $
we forced one block of Cohen’s,
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})$
, and for every
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})$
, and for every
![]() $\alpha <\kappa ^{++}$
,
$\alpha <\kappa ^{++}$
,
Indeed, in the Woodin and Ben-Shalom argument we first build the generic
![]() $G_{\kappa _1}$
up to
$G_{\kappa _1}$
up to
![]() $\kappa _1$
not including
$\kappa _1$
not including
![]() $\kappa _1$
in the same standard fashion as in [Reference Cummings, Foreman and Kanamori12]. The original construction of Woodin or Ben-Shalom of the Cohen generic
$\kappa _1$
in the same standard fashion as in [Reference Cummings, Foreman and Kanamori12]. The original construction of Woodin or Ben-Shalom of the Cohen generic
![]() $F_{\kappa _1}$
which is
$F_{\kappa _1}$
which is
![]() $M_1[G_{\kappa _1}]$
-generic for
$M_1[G_{\kappa _1}]$
-generic for
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})^{M_1[G_{\kappa _1}]}$
applies in our case, as it only uses the fact that
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})^{M_1[G_{\kappa _1}]}$
applies in our case, as it only uses the fact that
![]() $M_1[G_{\kappa _1}]$
is closed under
$M_1[G_{\kappa _1}]$
is closed under
![]() $\kappa $
-sequences and properties of
$\kappa $
-sequences and properties of
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})$
. Since
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})$
. Since
we can split the generic
![]() $F_{\kappa _1}$
and assume it is of the form
$F_{\kappa _1}$
and assume it is of the form
![]() $F_{\kappa _1}\times H_{\kappa _1}$
, which is
$F_{\kappa _1}\times H_{\kappa _1}$
, which is
![]() $M_1[G_{\kappa _1}]$
-generic for
$M_1[G_{\kappa _1}]$
-generic for
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})\times \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})$
. Work inside
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})\times \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})$
. Work inside
![]() $V[G_{\kappa }*F_\kappa ]$
, and modify the values of
$V[G_{\kappa }*F_\kappa ]$
, and modify the values of
![]() $F_{\kappa _1}$
and
$F_{\kappa _1}$
and
![]() $H_{\kappa _1}$
, as in the previous section so that for every
$H_{\kappa _1}$
, as in the previous section so that for every
![]() $\alpha <\kappa ^{++}$
,
$\alpha <\kappa ^{++}$
,
and for every
![]() $\alpha <\kappa ^{++}$
,
$\alpha <\kappa ^{++}$
,
![]() $f_{\kappa _1,j_1(\alpha )}(\kappa )=\alpha $
.
$f_{\kappa _1,j_1(\alpha )}(\kappa )=\alpha $
.
Lift
![]() $j_1$
to the embedding
$j_1$
to the embedding
![]() $j_1\subseteq j_1^*:V[G_{\kappa +1}]\rightarrow M_E[G_{\kappa _1}*F_{\kappa _1}]$
. Note that
$j_1\subseteq j_1^*:V[G_{\kappa +1}]\rightarrow M_E[G_{\kappa _1}*F_{\kappa _1}]$
. Note that
![]() $H_{\kappa _1}$
will be used only later. Set
$H_{\kappa _1}$
will be used only later. Set
then
![]() $U\subseteq U^*$
and
$U\subseteq U^*$
and
![]() $j^*_1$
is actually the ultrapower embedding by
$j^*_1$
is actually the ultrapower embedding by
![]() $U^*$
. Continuing as before, consider the second ultrapower (of V) by E. Denote
$U^*$
. Continuing as before, consider the second ultrapower (of V) by E. Denote
![]() $M_E$
by
$M_E$
by
![]() $M_1$
and
$M_1$
and
![]() $\mathrm {Ult}(M_E, j_E(E))$
by
$\mathrm {Ult}(M_E, j_E(E))$
by
![]() $M_2$
,
$M_2$
,
![]() $j_{2,1}=j_{j_1(E)}:M_1\rightarrow M_2$
the ultrapower embedding. Also, let
$j_{2,1}=j_{j_1(E)}:M_1\rightarrow M_2$
the ultrapower embedding. Also, let
![]() $ E_1=j_1(E)$
and
$ E_1=j_1(E)$
and
![]() $\kappa _2=j_{2,1}(\kappa _1)$
. Let
$\kappa _2=j_{2,1}(\kappa _1)$
. Let
![]() $j_2:V\to M_2$
be the composition of
$j_2:V\to M_2$
be the composition of
![]() $j_1$
with
$j_1$
with
![]() $j_{2,1}$
. The extension of
$j_{2,1}$
. The extension of
![]() $j_{2,1}$
will be such that at
$j_{2,1}$
will be such that at
![]() $\kappa _1$
we force with
$\kappa _1$
we force with
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})\times \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})$
part of the Lottery sum. To realize this, we define in
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})\times \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})$
part of the Lottery sum. To realize this, we define in
![]() $M_1[G_{\kappa _1}*(F_{\kappa _1}\times H_{\kappa _1})]$
we take the generic
$M_1[G_{\kappa _1}*(F_{\kappa _1}\times H_{\kappa _1})]$
we take the generic
![]() $G_{\kappa _1}$
up to
$G_{\kappa _1}$
up to
![]() $\kappa _1$
. At
$\kappa _1$
. At
![]() $\kappa _1$
we take
$\kappa _1$
we take
![]() $F_{\kappa _1}\times H_{\kappa _1}$
, then in
$F_{\kappa _1}\times H_{\kappa _1}$
, then in
![]() $M_1[G_{\kappa _1}*(F_{\kappa _1}\times H_{\kappa _1})]$
we construct as in Woodin and Ben-shalom argument in
$M_1[G_{\kappa _1}*(F_{\kappa _1}\times H_{\kappa _1})]$
we construct as in Woodin and Ben-shalom argument in
![]() $V[G_{\kappa }*F_\kappa ]$
an
$V[G_{\kappa }*F_\kappa ]$
an
![]() $M_2[G_{\kappa _1}*(F_{\kappa _1}\times H_{\kappa _1})]$
-generic
$M_2[G_{\kappa _1}*(F_{\kappa _1}\times H_{\kappa _1})]$
-generic
![]() $G_{(\kappa _1,\kappa _2)}*F_{\kappa _2}$
such that
$G_{(\kappa _1,\kappa _2)}*F_{\kappa _2}$
such that
![]() $j_{2,1}^{\prime \prime }G_{\kappa _1}*F_{\kappa _1}\subseteq G_{\kappa _2}*F_{\kappa _2}$
. Denote by
$j_{2,1}^{\prime \prime }G_{\kappa _1}*F_{\kappa _1}\subseteq G_{\kappa _2}*F_{\kappa _2}$
. Denote by
![]() ${\langle } f_{\kappa _2,\alpha }\mid \alpha <(\kappa _2^{++})^{M_2}{\rangle }$
the Cohen function induced by
${\langle } f_{\kappa _2,\alpha }\mid \alpha <(\kappa _2^{++})^{M_2}{\rangle }$
the Cohen function induced by
![]() $F_{\kappa _2}$
. We also secure that for every
$F_{\kappa _2}$
. We also secure that for every
![]() $\alpha <(\kappa _1^{++})^{M_1}$
:
$\alpha <(\kappa _1^{++})^{M_1}$
:
-
(1)
 $f_{\kappa _2 k(\alpha )}(\kappa _1)=\alpha \cdot 2+1$
, if
$f_{\kappa _2 k(\alpha )}(\kappa _1)=\alpha \cdot 2+1$
, if
 $\alpha \in j_E^{\prime \prime }\kappa ^{++}$
.
$\alpha \in j_E^{\prime \prime }\kappa ^{++}$
. -
(2)
 $f_{\kappa _2 k(\alpha )}(\kappa _1)=\alpha \cdot 2$
, if
$f_{\kappa _2 k(\alpha )}(\kappa _1)=\alpha \cdot 2$
, if
 $\alpha \in (\kappa _1^{++})^{M_1}\setminus j_E^{\prime \prime }\kappa ^{++}$
.
$\alpha \in (\kappa _1^{++})^{M_1}\setminus j_E^{\prime \prime }\kappa ^{++}$
. -
(3)
 $f_{\kappa _2,\kappa _1}(\kappa _1)=\kappa $
.
$f_{\kappa _2,\kappa _1}(\kappa _1)=\kappa $
.
Formally, given
![]() $p \in (\operatorname {\mathrm {Cohen}}(\kappa _2, (\kappa _2)^{++}))^{M_2[G_{\kappa _2}]}$
, define
$p \in (\operatorname {\mathrm {Cohen}}(\kappa _2, (\kappa _2)^{++}))^{M_2[G_{\kappa _2}]}$
, define
![]() $p^*$
such that
$p^*$
such that
![]() $\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and
$\operatorname {\mathrm {dom}}(p^*)=\operatorname {\mathrm {dom}}(p)$
and
 $$ \begin{align*}p^*({\langle}\gamma,\beta{\rangle})=\begin{cases} f_{\kappa_1,\alpha}(\gamma), & \gamma<\kappa_1\wedge \beta=k(\alpha),\\ \alpha\cdot 2+1, & \gamma=\kappa_1\wedge \beta=k(\alpha)\wedge \alpha\in j^{\prime\prime}_E\kappa^{++},\\ \alpha\cdot 2, & \gamma=\kappa_1\wedge \beta=k(\alpha)\wedge \alpha\in (\kappa_1^{++})^{M_1}\setminus j_E^{\prime\prime}\kappa^{++},\\ \kappa, & \alpha=\gamma=\kappa_1,\\ p({\langle}\gamma,\alpha{\rangle}), & \text{otherwise}.\end{cases}\end{align*} $$
$$ \begin{align*}p^*({\langle}\gamma,\beta{\rangle})=\begin{cases} f_{\kappa_1,\alpha}(\gamma), & \gamma<\kappa_1\wedge \beta=k(\alpha),\\ \alpha\cdot 2+1, & \gamma=\kappa_1\wedge \beta=k(\alpha)\wedge \alpha\in j^{\prime\prime}_E\kappa^{++},\\ \alpha\cdot 2, & \gamma=\kappa_1\wedge \beta=k(\alpha)\wedge \alpha\in (\kappa_1^{++})^{M_1}\setminus j_E^{\prime\prime}\kappa^{++},\\ \kappa, & \alpha=\gamma=\kappa_1,\\ p({\langle}\gamma,\alpha{\rangle}), & \text{otherwise}.\end{cases}\end{align*} $$
In
![]() $V[G_{\kappa +1}]$
,
$V[G_{\kappa +1}]$
,
![]() $|\operatorname {\mathrm {dom}}(p)\cap j^{\prime \prime }_{E^2}\kappa ^{++}|\leq \kappa $
and
$|\operatorname {\mathrm {dom}}(p)\cap j^{\prime \prime }_{E^2}\kappa ^{++}|\leq \kappa $
and
![]() $M_1[G_{\kappa _1+1}]$
is closed under
$M_1[G_{\kappa _1+1}]$
is closed under
![]() $\kappa $
-sequences, hence
$\kappa $
-sequences, hence
![]() $p^*\in M_1[G_{\kappa _1+1}]$
. The argument we have seen before applied in
$p^*\in M_1[G_{\kappa _1+1}]$
. The argument we have seen before applied in
![]() $M_1[G_{\kappa _1+1}]$
, thus
$M_1[G_{\kappa _1+1}]$
, thus
This implies that
![]() $p^*\in M_2[G_{\kappa _2+1}]$
since
$p^*\in M_2[G_{\kappa _2+1}]$
since
![]() $M_2[G_{\kappa _2+1}]$
is closed under
$M_2[G_{\kappa _2+1}]$
is closed under
![]() $\kappa _1$
-sequences from
$\kappa _1$
-sequences from
![]() $M_1[G_{\kappa _1+1}]$
.
$M_1[G_{\kappa _1+1}]$
.
Extend in
![]() $V[G_{\kappa }*F_\kappa ]$
,
$V[G_{\kappa }*F_\kappa ]$
,
![]() $j_{2,1}\subseteq j^*_2:M_1[G_{\kappa _1}*F_{\kappa _1}\rightarrow M_2[G_{\kappa _2}*F_{\kappa _2}]$
and let
$j_{2,1}\subseteq j^*_2:M_1[G_{\kappa _1}*F_{\kappa _1}\rightarrow M_2[G_{\kappa _2}*F_{\kappa _2}]$
and let
![]() $j^*_2:V[G_{\kappa }*F_\kappa ]\rightarrow M_2[G_{\kappa _2}*F_{\kappa _2}]$
be the composition
$j^*_2:V[G_{\kappa }*F_\kappa ]\rightarrow M_2[G_{\kappa _2}*F_{\kappa _2}]$
be the composition
![]() $j^*_{2,1}\circ j_1^*$
. Note that
$j^*_{2,1}\circ j_1^*$
. Note that
![]() $j_{2,1}^*$
is definable only in
$j_{2,1}^*$
is definable only in
![]() $V[G_{\kappa }*(F_{\kappa }]$
. Denote by
$V[G_{\kappa }*(F_{\kappa }]$
. Denote by
![]() $V[G_{\kappa }*F_\kappa ]=V^*$
, define
$V[G_{\kappa }*F_\kappa ]=V^*$
, define
Claim 3.4.
W is a
![]() $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
![]() $\kappa $
such that:
$\kappa $
such that:
-
(1)
 $j_W=j^*_2$
,
$j_W=j^*_2$
,
 $[id]_W=\kappa _1$
,
$[id]_W=\kappa _1$
,
 $U^*\leq _{R-K}W$
.
$U^*\leq _{R-K}W$
. -
(2)
 $Cub_\kappa \subseteq W$
,
$Cub_\kappa \subseteq W$
,
 $\{\alpha <\kappa \mid {\mathrm {cf}}(\alpha )=\alpha )\}\in W$
.
$\{\alpha <\kappa \mid {\mathrm {cf}}(\alpha )=\alpha )\}\in W$
. -
(3)
 $L_0:=\{\beta <\kappa \mid \operatorname {\mathrm {Cohen}}(\beta ,\beta ^{++})\times \operatorname {\mathrm {Cohen}}(\beta ,\beta ^{++})\text { was forced in }G_{\kappa +1}\}\in W.$
$L_0:=\{\beta <\kappa \mid \operatorname {\mathrm {Cohen}}(\beta ,\beta ^{++})\times \operatorname {\mathrm {Cohen}}(\beta ,\beta ^{++})\text { was forced in }G_{\kappa +1}\}\in W.$
-
(4) For every
 $\alpha <\kappa ^{++}$
,
$\alpha <\kappa ^{++}$
,
 $L_{1,\alpha }:=\{\nu <\kappa \mid f_{\kappa ,\alpha }(\nu )<\nu ^{++}\}\in W$
.
$L_{1,\alpha }:=\{\nu <\kappa \mid f_{\kappa ,\alpha }(\nu )<\nu ^{++}\}\in W$
. -
(5) The sequence
 ${\langle } A_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
is a strong witness for
${\langle } A_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
is a strong witness for
 $\neg \text {Gal}(W,\kappa ,\kappa ^{++})$
. Moreover, the sequence
$\neg \text {Gal}(W,\kappa ,\kappa ^{++})$
. Moreover, the sequence
 ${\langle } A_\alpha \cap L_{1,\alpha }\mid \alpha <\kappa ^{++}{\rangle }$
is a witness for
${\langle } A_\alpha \cap L_{1,\alpha }\mid \alpha <\kappa ^{++}{\rangle }$
is a witness for
 $\neg \text {Gal}(W,\kappa ,\kappa ^{++})$
.
$\neg \text {Gal}(W,\kappa ,\kappa ^{++})$
.
Proof
![]() $(1),(2),$
and the first part of
$(1),(2),$
and the first part of
![]() $(5)$
are the same argument as in Claim 3.2. As for
$(5)$
are the same argument as in Claim 3.2. As for
![]() $(3)$
, note that we have constructed the generic
$(3)$
, note that we have constructed the generic
![]() $G_{\kappa _2+1}=j^*_2(G_{\kappa +1})$
so that on
$G_{\kappa _2+1}=j^*_2(G_{\kappa +1})$
so that on
![]() $\kappa _1$
we have forced
$\kappa _1$
we have forced
![]() $\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})\times \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})$
. To see
$\operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})\times \operatorname {\mathrm {Cohen}}(\kappa _1,\kappa _1^{++})$
. To see
![]() $(4)$
, for every
$(4)$
, for every
![]() $\alpha <\kappa ^{++}$
,
$\alpha <\kappa ^{++}$
,
Hence by elementarity,
![]() $\kappa _1\in j^*_2(L_{1,\alpha })$
. Finally, the moreover part of
$\kappa _1\in j^*_2(L_{1,\alpha })$
. Finally, the moreover part of
![]() $(5)$
, toward a contradiction if there would be a set
$(5)$
, toward a contradiction if there would be a set
![]() $I\in [\kappa ^{++}]^{\kappa }$
such that
$I\in [\kappa ^{++}]^{\kappa }$
such that
![]() $\cap _{i\in I}A_\alpha \cap L_{1,\alpha }\in W$
then clearly
$\cap _{i\in I}A_\alpha \cap L_{1,\alpha }\in W$
then clearly
![]() $\cap _{i\in I}A_\alpha \in W$
, contradicting the first part of
$\cap _{i\in I}A_\alpha \in W$
, contradicting the first part of
![]() $(5)$
that
$(5)$
that
![]() $A_\alpha $
’s form a witness for
$A_\alpha $
’s form a witness for
![]() $\neg \text {Gal}(W,\kappa ,\kappa ^{++})$
.
$\neg \text {Gal}(W,\kappa ,\kappa ^{++})$
.
Denoted by
![]() $\nu \mapsto \pi _{nor}(\nu )$
the Rudin–Keisler projection from W to
$\nu \mapsto \pi _{nor}(\nu )$
the Rudin–Keisler projection from W to
![]() $U^*$
, and let us prove that W witnesses the theorem:
$U^*$
, and let us prove that W witnesses the theorem:
Proposition 3.5. Let
![]() $H\subseteq \operatorname {\mathrm {Prikry}}(W)$
be a
$H\subseteq \operatorname {\mathrm {Prikry}}(W)$
be a
![]() $V^*$
-generic filter. There is
$V^*$
-generic filter. There is
![]() $G^*\in V^*[H]$
which is
$G^*\in V^*[H]$
which is
![]() $V^*$
-generic for
$V^*$
-generic for
![]() $Cohen(\kappa ,\kappa ^{++})^{V^*}$
.
$Cohen(\kappa ,\kappa ^{++})^{V^*}$
.
Proof of Proposition 3.5
Let
![]() ${\langle } c_n \mid n<\omega {\rangle } $
be the W-Prikry sequence corresponding to H. Suppose without loss of generality that for every
${\langle } c_n \mid n<\omega {\rangle } $
be the W-Prikry sequence corresponding to H. Suppose without loss of generality that for every
![]() $n<\omega $
,
$n<\omega $
,
![]() $c_n\in L_0$
.
$c_n\in L_0$
.
Define, for every
![]() $n<\omega $
, the set
$n<\omega $
, the set
For every
![]() $\alpha <\kappa ^{++}$
, let
$\alpha <\kappa ^{++}$
, let
![]() $n_\alpha $
be the unique n such that
$n_\alpha $
be the unique n such that
![]() $\alpha \in Z_n$
. Let
$\alpha \in Z_n$
. Let
![]() $\alpha <\kappa ^+$
, and define
$\alpha <\kappa ^+$
, and define
![]() $f^*_\alpha :\kappa \to \kappa $
as follows:
$f^*_\alpha :\kappa \to \kappa $
as follows:
Denote by
the generic
![]() $c_n$
-Cohen functions forced by G and define the function
$c_n$
-Cohen functions forced by G and define the function
![]() $f^*_\alpha :\kappa \rightarrow \kappa $
by
$f^*_\alpha :\kappa \rightarrow \kappa $
by
 $$ \begin{align*}f^*_\alpha=h_{c_{n_\alpha},f_{\kappa,\alpha}(c_{n_\alpha})}\cup\left(\bigcup_{n_\alpha<n<\omega}h_{c_n,f_{\kappa,\alpha}(c_n)}\restriction[c_{n-1},c_n)\right).\end{align*} $$
$$ \begin{align*}f^*_\alpha=h_{c_{n_\alpha},f_{\kappa,\alpha}(c_{n_\alpha})}\cup\left(\bigcup_{n_\alpha<n<\omega}h_{c_n,f_{\kappa,\alpha}(c_n)}\restriction[c_{n-1},c_n)\right).\end{align*} $$
Note that the Cohen functions on
![]() $\kappa $
play the role of the canonical functions from the previous section. Let us prove that
$\kappa $
play the role of the canonical functions from the previous section. Let us prove that
![]() $F={\langle } f^*_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
are Cohen generic functions over
$F={\langle } f^*_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
are Cohen generic functions over
![]() $V^*$
.
$V^*$
.
Claim 3.6. Let
![]() $G^*=\{p\in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})^{V^*}\mid p\subseteq F\}$
, then
$G^*=\{p\in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})^{V^*}\mid p\subseteq F\}$
, then
![]() $G^*$
is a
$G^*$
is a
![]() $V^*$
-generic filter.
$V^*$
-generic filter.
Let
![]() $\mathcal {A}\in V^*$
be a maximal antichain in the forcing
$\mathcal {A}\in V^*$
be a maximal antichain in the forcing
![]() $\operatorname {\mathrm {Cohen}}(\kappa , \kappa ^{++})^{V^*}$
. Note that since
$\operatorname {\mathrm {Cohen}}(\kappa , \kappa ^{++})^{V^*}$
. Note that since
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})^{V^*}$
is
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})^{V^*}$
is
![]() $\kappa $
-closed then
$\kappa $
-closed then
By
![]() $\kappa ^+$
-cc of the forcing, there is
$\kappa ^+$
-cc of the forcing, there is
![]() $Y'\subseteq \kappa ^{++}$
,
$Y'\subseteq \kappa ^{++}$
,
![]() $Y'\in V$
such that
$Y'\in V$
such that
![]() $|Y'|=\kappa $
and
$|Y'|=\kappa $
and
![]() $\mathcal {A}\subseteq \operatorname {\mathrm {Cohen}}(\kappa ,Y')^{V^*}$
. Also, since
$\mathcal {A}\subseteq \operatorname {\mathrm {Cohen}}(\kappa ,Y')^{V^*}$
. Also, since
![]() $|\mathcal {A}|=\kappa $
,
$|\mathcal {A}|=\kappa $
,
![]() $\mathcal {A}\in V[G_\kappa *F_\kappa ]$
, there is
$\mathcal {A}\in V[G_\kappa *F_\kappa ]$
, there is
![]() $Z\subseteq \kappa ^{++}$
such that
$Z\subseteq \kappa ^{++}$
such that
![]() $|Z|=\kappa $
such that
$|Z|=\kappa $
such that
![]() $\mathcal {A}\in V[G_\kappa *F_\kappa \restriction Z]$
. Without loss of generality assume that
$\mathcal {A}\in V[G_\kappa *F_\kappa \restriction Z]$
. Without loss of generality assume that
![]() $Z=Y\in V$
. Let
$Z=Y\in V$
. Let
![]() $V\ni \phi :\kappa \rightarrow Y$
be a bijection.
$V\ni \phi :\kappa \rightarrow Y$
be a bijection.
As in Claim 2.13, we can construct an
![]() $\in $
-increasing continuous chain
$\in $
-increasing continuous chain
![]() ${\langle } N_\beta \mid \beta <\kappa {\rangle }\in V^*$
of elementary submodels of
${\langle } N_\beta \mid \beta <\kappa {\rangle }\in V^*$
of elementary submodels of
![]() $H_\chi $
such that:
$H_\chi $
such that:
-
(1)
 $|N_\beta |<\kappa $
.
$|N_\beta |<\kappa $
. -
(2)
 $G_{\kappa +1},\mathcal {A},\phi ,Y\in N_0$
.
$G_{\kappa +1},\mathcal {A},\phi ,Y\in N_0$
. -
(3)
 $N_\beta \cap \kappa =\gamma _\beta $
is a cardinal
$N_\beta \cap \kappa =\gamma _\beta $
is a cardinal
 $<\kappa $
, and
$<\kappa $
, and
 $\gamma _{\beta +1}$
is regular.
$\gamma _{\beta +1}$
is regular. -
(4) If
 $\gamma _\beta $
is regular, then
$\gamma _\beta $
is regular, then
 $\operatorname {\mathrm {Cohen}}(\gamma _\beta ,\phi "\gamma _\beta )=\operatorname {\mathrm {Cohen}}(\kappa ,Y)\cap N_\beta $
.
$\operatorname {\mathrm {Cohen}}(\gamma _\beta ,\phi "\gamma _\beta )=\operatorname {\mathrm {Cohen}}(\kappa ,Y)\cap N_\beta $
.
Set
This is club in
![]() $\kappa $
since the sequence
$\kappa $
since the sequence
![]() $\gamma _\beta $
is continuous and since the set
$\gamma _\beta $
is continuous and since the set
![]() $\{\beta \mid \gamma _\beta =\beta \}$
is a club.
$\{\beta \mid \gamma _\beta =\beta \}$
is a club.
Recall that by construction
![]() $j^*_2({\langle } f_{\kappa ,\alpha }\mid \alpha <\kappa ^{++}{\rangle })={\langle } f_{\kappa _2,\alpha }\mid \alpha <\kappa _2^{++}{\rangle }$
. Also, for every
$j^*_2({\langle } f_{\kappa ,\alpha }\mid \alpha <\kappa ^{++}{\rangle })={\langle } f_{\kappa _2,\alpha }\mid \alpha <\kappa _2^{++}{\rangle }$
. Also, for every
![]() $\nu \in j_2(\phi )"\kappa _1$
there is
$\nu \in j_2(\phi )"\kappa _1$
there is
![]() $\gamma <\kappa _1$
such that
$\gamma <\kappa _1$
such that
![]() $\nu =j_2(\phi )(\gamma )$
, and since
$\nu =j_2(\phi )(\gamma )$
, and since
![]() $crit(j_{2,1})=\kappa _1$
,
$crit(j_{2,1})=\kappa _1$
,
![]() $\nu =j_{2,1}(j_1(\phi )(\gamma ))$
. Since
$\nu =j_{2,1}(j_1(\phi )(\gamma ))$
. Since
![]() $j_1(\phi ):\kappa _1\rightarrow \kappa _1^{++}$
we conclude that
$j_1(\phi ):\kappa _1\rightarrow \kappa _1^{++}$
we conclude that
![]() $\nu =j_{2,1}(\alpha )$
for some
$\nu =j_{2,1}(\alpha )$
for some
![]() $\alpha <(\kappa _1^{++})^{M_1}$
which implies that
$\alpha <(\kappa _1^{++})^{M_1}$
which implies that
Since
![]() $\phi $
is a bijection, for every distinct
$\phi $
is a bijection, for every distinct
![]() $\nu _1,\nu _2\in j_2(\phi )"\kappa _1$
,
$\nu _1,\nu _2\in j_2(\phi )"\kappa _1$
,
![]() $f_{\kappa _2,\nu _1}(\kappa _1)\neq f_{\kappa _2,\nu _2}(\kappa _1)$
. Reflecting this, we obtain that the set
$f_{\kappa _2,\nu _1}(\kappa _1)\neq f_{\kappa _2,\nu _2}(\kappa _1)$
. Reflecting this, we obtain that the set
Also, by construction, for every
![]() $\alpha <\kappa _1^{++}$
,
$\alpha <\kappa _1^{++}$
,
![]() $f_{\kappa _2,j_{2,1}(\alpha )}\restriction \kappa _1=f_{\kappa _1,\alpha }$
and therefore for every
$f_{\kappa _2,j_{2,1}(\alpha )}\restriction \kappa _1=f_{\kappa _1,\alpha }$
and therefore for every
![]() $\alpha \in j_2(\phi )"\kappa _1$
, there is
$\alpha \in j_2(\phi )"\kappa _1$
, there is
![]() $\nu <\kappa _1^{++}$
such that
$\nu <\kappa _1^{++}$
such that
and
![]() $j_1(\phi )(\nu )<\kappa _1^{++}$
. Hence
$j_1(\phi )(\nu )<\kappa _1^{++}$
. Hence
![]() $f_{\kappa _2,\alpha }\restriction \kappa _1=f_{\kappa _1,\beta }$
for some
$f_{\kappa _2,\alpha }\restriction \kappa _1=f_{\kappa _1,\beta }$
for some
![]() $\beta <\kappa _1^{++}$
. Reflecting this we obtain that the set
$\beta <\kappa _1^{++}$
. Reflecting this we obtain that the set
Now the argument of Claim 2.15 applies since for every
![]() $\nu _0\in C\cap E\cap F$
,
$\nu _0\in C\cap E\cap F$
,
![]() $\forall \tau _1<\tau _2\in \phi "\nu _0$
,
$\forall \tau _1<\tau _2\in \phi "\nu _0$
,
![]() $f_{\kappa ,\tau _1}(\nu _0)\neq f_{\kappa ,\tau _2}(\nu _0)$
, hence
$f_{\kappa ,\tau _1}(\nu _0)\neq f_{\kappa ,\tau _2}(\nu _0)$
, hence
![]() ${\langle } h_{\nu _0,f_{\kappa ,\tau }(\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
are distinct mutually
${\langle } h_{\nu _0,f_{\kappa ,\tau }(\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
are distinct mutually
![]() $V[G_{\nu _0}*F_{\nu _0}]$
-generic Cohen functions over
$V[G_{\nu _0}*F_{\nu _0}]$
-generic Cohen functions over
![]() $\nu _0$
. Thus, we can find
$\nu _0$
. Thus, we can find
![]() $d\in \mathcal {A}\cap \operatorname {\mathrm {Cohen}}(\nu _0,\nu _0^{++})$
such that d is extended by
$d\in \mathcal {A}\cap \operatorname {\mathrm {Cohen}}(\nu _0,\nu _0^{++})$
such that d is extended by
![]() ${\langle } h_{\nu _0,f_{\kappa ,\alpha }(\nu _0)}\mid \alpha \in \phi "\nu _0{\rangle }$
. Finally we note that
${\langle } h_{\nu _0,f_{\kappa ,\alpha }(\nu _0)}\mid \alpha \in \phi "\nu _0{\rangle }$
. Finally we note that
Let
![]() $p={\langle } {\langle }{\rangle }, B{\rangle }$
be a condition, shrink B to
$p={\langle } {\langle }{\rangle }, B{\rangle }$
be a condition, shrink B to
![]() $B_0:=B\cap C\cap E\cap F\cap R\in W$
, and pick now any
$B_0:=B\cap C\cap E\cap F\cap R\in W$
, and pick now any
![]() $\nu _0\in B_0$
. Split
$\nu _0\in B_0$
. Split
![]() $\phi "\nu _0$
into two sets:
$\phi "\nu _0$
into two sets:
Since
![]() $\nu _0\in R$
we have that
$\nu _0\in R$
we have that
![]() $X_1\subseteq \phi "(\pi _{nor}(\nu _0),\nu _0)$
. The condition
$X_1\subseteq \phi "(\pi _{nor}(\nu _0),\nu _0)$
. The condition
![]() $p_0={\langle } {\langle } \nu _0{\rangle }, B_0\cap (\bigcap _{\tau \in \phi "\nu _0}A_\tau ){\rangle }$
forces the following:
$p_0={\langle } {\langle } \nu _0{\rangle }, B_0\cap (\bigcap _{\tau \in \phi "\nu _0}A_\tau ){\rangle }$
forces the following:
-
(1) The Prikry sequence is included in each
 $A_\tau $
,
$A_\tau $
,
 $\tau \in X^{\nu _0}_0$
, i.e.,
$\tau \in X^{\nu _0}_0$
, i.e.,
 $n_\tau =0$
.
$n_\tau =0$
. -
(2)
 $n_\tau =1$
, for every
$n_\tau =1$
, for every
 $\tau \in X^{\nu _0}_1$
.
$\tau \in X^{\nu _0}_1$
.
In particular, this condition forces some information about the Cohen functions. Namely that:
-
(1) For
 $\tau \in X_0^{\nu _0}$
,
$\tau \in X_0^{\nu _0}$
,
 $f^*_{\tau }\restriction \nu _0=h_{\nu _0,f_{\kappa ,\tau }(\nu _0)}$
.
$f^*_{\tau }\restriction \nu _0=h_{\nu _0,f_{\kappa ,\tau }(\nu _0)}$
. -
(2) For
 $\tau \in X_1^{\nu _0}$
,
$\tau \in X_1^{\nu _0}$
,
 .
.
We would like to find a condition in
![]() $\mathcal {A}$
which is below these decided parts of the Cohen. By the previous paragraph, there is
$\mathcal {A}$
which is below these decided parts of the Cohen. By the previous paragraph, there is
![]() $d\in N_{\nu _0}\cap \operatorname {\mathrm {Cohen}}(\kappa ,Y)=\operatorname {\mathrm {Cohen}}(\nu _0,\phi "\nu _0)$
, which is extended by
$d\in N_{\nu _0}\cap \operatorname {\mathrm {Cohen}}(\kappa ,Y)=\operatorname {\mathrm {Cohen}}(\nu _0,\phi "\nu _0)$
, which is extended by
![]() ${\langle } h_{\nu _0,f_{\kappa ,\tau }(\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
. As before we will need to pick
${\langle } h_{\nu _0,f_{\kappa ,\tau }(\nu _0)}\mid \tau \in \phi "\nu _0{\rangle }$
. As before we will need to pick
![]() $\nu _0,\nu _1$
so that
$\nu _0,\nu _1$
so that
![]() $d^{\nu _0}\in G^*$
.
$d^{\nu _0}\in G^*$
.
Let
be a name in V for
![]() $B_0$
. We fix a condition
$B_0$
. We fix a condition
![]() $m_0\in G_\kappa *F_\kappa $
which forces that if
$m_0\in G_\kappa *F_\kappa $
which forces that if
then there is
which is extended by
, and
. Recall that by the construction of
![]() $G_{\kappa _2}$
, we have
$G_{\kappa _2}$
, we have
![]() $m_0\in G_{\kappa _2}*F_{\kappa _2}$
. Let
$m_0\in G_{\kappa _2}*F_{\kappa _2}$
. Let
![]() $ m_0\leq t\in G_{\kappa _2}*F_{\kappa _2}$
be a condition such that
$ m_0\leq t\in G_{\kappa _2}*F_{\kappa _2}$
be a condition such that
By the construction of
![]() $G_{\kappa _2}*F_{\kappa _2}$
, t has the form:
$G_{\kappa _2}*F_{\kappa _2}$
, t has the form:
 $$ \begin{align*}t={\langle} t_{<\kappa}, t_{\kappa},t_{(\kappa,\kappa_1)},\underset{t_{\kappa_1}}{\underbrace{{\langle} t_{\kappa_1}^0,t_{\kappa_1}^1{\rangle}}},t_{(\kappa_1,\kappa_2)},t_{\kappa_2}{\rangle}.\end{align*} $$
$$ \begin{align*}t={\langle} t_{<\kappa}, t_{\kappa},t_{(\kappa,\kappa_1)},\underset{t_{\kappa_1}}{\underbrace{{\langle} t_{\kappa_1}^0,t_{\kappa_1}^1{\rangle}}},t_{(\kappa_1,\kappa_2)},t_{\kappa_2}{\rangle}.\end{align*} $$
Distinguishing from the case of
![]() $\kappa ^+$
, we now have that
$\kappa ^+$
, we now have that
![]() $f_{\kappa _2,j_2(\alpha )}(\kappa _1)=j_1(\alpha )\cdot 2+1$
for every
$f_{\kappa _2,j_2(\alpha )}(\kappa _1)=j_1(\alpha )\cdot 2+1$
for every
![]() $\alpha <\kappa ^+$
; this will hold for every
$\alpha <\kappa ^+$
; this will hold for every
![]() $\alpha \in \phi "\kappa $
as well. Also, recall that
$\alpha \in \phi "\kappa $
as well. Also, recall that
![]() $Y\in V$
, hence
$Y\in V$
, hence
![]() $\phi \in V$
. Thus
$\phi \in V$
. Thus
![]() $j_2(\phi )\in M_2$
and
$j_2(\phi )\in M_2$
and
![]() $j_2(\phi )"\kappa \in M_2$
. Also, for
$j_2(\phi )"\kappa \in M_2$
. Also, for
![]() $(t_{\kappa _2})_{G_{\kappa _2}}\in M_2[G_{\kappa _2}]$
,
$(t_{\kappa _2})_{G_{\kappa _2}}\in M_2[G_{\kappa _2}]$
,
and
![]() $(t_{\kappa _2})_{G_{\kappa _2}}\restriction \kappa \times \{j_2(\alpha )\}\subseteq f_{\kappa ,\alpha }$
. We also fix
$(t_{\kappa _2})_{G_{\kappa _2}}\restriction \kappa \times \{j_2(\alpha )\}\subseteq f_{\kappa ,\alpha }$
. We also fix
![]() $X\in V$
,
$X\in V$
,
![]() $X\subseteq \kappa ^{++}$
,
$X\subseteq \kappa ^{++}$
,
![]() $|N_0|\leq \kappa $
such that
$|N_0|\leq \kappa $
such that
![]() $\operatorname {\mathrm {Supp}}((t_{\kappa _2})_{G_{\kappa _2}})\subseteq j_2(N_0)$
.
$\operatorname {\mathrm {Supp}}((t_{\kappa _2})_{G_{\kappa _2}})\subseteq j_2(N_0)$
.
Therefore, we can extend if necessary t such that:
Next consider
![]() $t_{\kappa _1}={\langle } t_{\kappa _1}^0,t_{\kappa _1}^1{\rangle }$
; it is a
$t_{\kappa _1}={\langle } t_{\kappa _1}^0,t_{\kappa _1}^1{\rangle }$
; it is a
![]() ${\mathcal P}_{\kappa _1}$
-name for a condition in
${\mathcal P}_{\kappa _1}$
-name for a condition in
![]() $F_{\kappa _1}\times H_{\kappa _1}$
. By the construction of the generic
$F_{\kappa _1}\times H_{\kappa _1}$
. By the construction of the generic
![]() $F_{\kappa _1}\times H_{\kappa _1}$
, for every
$F_{\kappa _1}\times H_{\kappa _1}$
, for every
![]() $\alpha <\kappa ^{++}$
, we made sure that,
$\alpha <\kappa ^{++}$
, we made sure that,
![]() $h_{\kappa _1,j_1(\alpha )2+1}\restriction \kappa =f_{\kappa ,\alpha }$
. Also,
$h_{\kappa _1,j_1(\alpha )2+1}\restriction \kappa =f_{\kappa ,\alpha }$
. Also,
![]() $(j_1(\phi )"\kappa )\cdot 2+1\in M_2$
Footnote
7
. Let
$(j_1(\phi )"\kappa )\cdot 2+1\in M_2$
Footnote
7
. Let
The fact that for every
![]() $\beta <\kappa ^{++}$
,
$\beta <\kappa ^{++}$
,
![]() $f_{\kappa _2,j_2(\beta )}(\kappa _1)=j_1(\beta )\cdot 2+1$
implies
$f_{\kappa _2,j_2(\beta )}(\kappa _1)=j_1(\beta )\cdot 2+1$
implies
Extend if necessary
![]() $t_{<\kappa _1}$
, and assume that
$t_{<\kappa _1}$
, and assume that
As for the lower part, due to the Easton support, we have
Fix functions
![]() $r,\Gamma _1$
which represent
$r,\Gamma _1$
which represent
![]() $t,\mu $
resp. in the ultrapower
$t,\mu $
resp. in the ultrapower
![]() $M_{E^2}$
, namely for some
$M_{E^2}$
, namely for some
![]() $\vec {\xi }\in [\kappa _1^{++}]^{<\omega }$
,
$\vec {\xi }\in [\kappa _1^{++}]^{<\omega }$
,
![]() $j_2(r)(\vec {\xi })=t, \ j_2(\Gamma _1)(\vec {\xi })=\mu $
. Without loss of generality, suppose that both
$j_2(r)(\vec {\xi })=t, \ j_2(\Gamma _1)(\vec {\xi })=\mu $
. Without loss of generality, suppose that both
![]() $\kappa $
and
$\kappa $
and
![]() $\kappa _1$
appear in
$\kappa _1$
appear in
![]() $\vec {\xi }$
,
$\vec {\xi }$
,
![]() $\kappa =\min (\vec {\xi })=\vec {\xi }(0)$
and
$\kappa =\min (\vec {\xi })=\vec {\xi }(0)$
and
![]() $\kappa _1=\vec {\xi }(i_0)$
. Then the functions
$\kappa _1=\vec {\xi }(i_0)$
. Then the functions
![]() $\vec {\nu }\in [\kappa ]^{|\vec {\xi }|}\mapsto (\vec {\nu }(0),\vec {\nu }(i_0))$
represent
$\vec {\nu }\in [\kappa ]^{|\vec {\xi }|}\mapsto (\vec {\nu }(0),\vec {\nu }(i_0))$
represent
![]() $(\kappa ,\kappa _1)$
. Without loss of generality, suppose that for every
$(\kappa ,\kappa _1)$
. Without loss of generality, suppose that for every
![]() $\vec {\nu }$
, it takes the form
$\vec {\nu }$
, it takes the form
Reflecting some of the properties of t we obtain a set
![]() $B'\in E(\vec {\xi })$
such that for every
$B'\in E(\vec {\xi })$
such that for every
![]() $\vec {\nu }\in B'$
:
$\vec {\nu }\in B'$
:
-
 $(1)_{\vec {\nu }}$
$(1)_{\vec {\nu }}$
 .
. -
 $(2a)_{\vec {\nu }}$
$(2a)_{\vec {\nu }}$
 $ r_{<\kappa }\Vdash (\vec {\nu }(0)\cup \{\vec {\nu }(i_0)\})\times \phi "\vec {\nu }(0) \subseteq \operatorname {\mathrm {dom}}(r_{\kappa })\wedge $
$ r_{<\kappa }\Vdash (\vec {\nu }(0)\cup \{\vec {\nu }(i_0)\})\times \phi "\vec {\nu }(0) \subseteq \operatorname {\mathrm {dom}}(r_{\kappa })\wedge $
 ${\langle }0,\vec {\nu }(i_0){\rangle }\in \operatorname {\mathrm {dom}}(r_{\kappa }) \wedge \operatorname {\mathrm {Supp}} (r_{\kappa })\subseteq N_0.$
${\langle }0,\vec {\nu }(i_0){\rangle }\in \operatorname {\mathrm {dom}}(r_{\kappa }) \wedge \operatorname {\mathrm {Supp}} (r_{\kappa })\subseteq N_0.$
-
 $(2b)_{\vec {\nu }}$
$(2b)_{\vec {\nu }}$
 $r_{<\kappa }\Vdash \forall \alpha \in \phi "\vec {\nu }(0).r_{\kappa ,\alpha }(\vec {\nu }(i_0))$
is odd and
$r_{<\kappa }\Vdash \forall \alpha \in \phi "\vec {\nu }(0).r_{\kappa ,\alpha }(\vec {\nu }(i_0))$
is odd and
 $r_{\kappa ,\vec {\nu }(i_0)}(0)=\vec {\nu }(0)$
.
$r_{\kappa ,\vec {\nu }(i_0)}(0)=\vec {\nu }(0)$
. -
 $(3)_{\vec {\nu }}$
$(3)_{\vec {\nu }}$
 $ r_{<\vec {\nu }(i_0)}\Vdash \vec {\nu }(0)\times \operatorname {\mathrm {dom}}(\Gamma _1(\vec {\nu }))\subseteq \operatorname {\mathrm {dom}}(r^1_{\vec {\nu }(i_0)})$
and for every
$ r_{<\vec {\nu }(i_0)}\Vdash \vec {\nu }(0)\times \operatorname {\mathrm {dom}}(\Gamma _1(\vec {\nu }))\subseteq \operatorname {\mathrm {dom}}(r^1_{\vec {\nu }(i_0)})$
and for every
 .
. -
 $(4)_{\vec {\nu }}$
$(4)_{\vec {\nu }}$
 $r_{<\vec {\nu }(0)}=t_{<\kappa }\in V_{\vec {\nu }(0)}$
.
$r_{<\vec {\nu }(0)}=t_{<\kappa }\in V_{\vec {\nu }(0)}$
.
Let
Since
![]() $B'\in E(\vec {\xi })$
we have that
$B'\in E(\vec {\xi })$
we have that
![]() $\vec {\xi }\in j_2(B')$
and since
$\vec {\xi }\in j_2(B')$
and since
![]() $j_2(r)(\vec {\xi })=t\in j^*_2(G_\kappa *F_\kappa )=G_{\kappa _2}*F_{\kappa _2}$
, we conclude that
$j_2(r)(\vec {\xi })=t\in j^*_2(G_\kappa *F_\kappa )=G_{\kappa _2}*F_{\kappa _2}$
, we conclude that
![]() $B"\in W$
. Also,
$B"\in W$
. Also,
![]() $B"\subseteq B_0$
by clause
$B"\subseteq B_0$
by clause
![]() $(1)$
.
$(1)$
.
We proceed by a density argument, and recall that by the definition of
![]() $G_2$
, we have that
$G_2$
, we have that
![]() ${\langle } t_{<\kappa },t_\kappa {\rangle }\in G_\kappa *F_\kappa $
.
${\langle } t_{<\kappa },t_\kappa {\rangle }\in G_\kappa *F_\kappa $
.
Claim 3.7. Let D be the set of all conditions
![]() $q\in \mathcal {P}_{\kappa +1}$
, such that there exist
$q\in \mathcal {P}_{\kappa +1}$
, such that there exist
![]() $\vec {\nu }_0,\vec {\nu }_1\in B', \ \vec {\nu }_1(0)>\vec {\nu }_0(i_0)$
, and a
$\vec {\nu }_0,\vec {\nu }_1\in B', \ \vec {\nu }_1(0)>\vec {\nu }_0(i_0)$
, and a
![]() $\mathcal {P}_{\vec {\nu }_0(i_0)}$
-name
$\mathcal {P}_{\vec {\nu }_0(i_0)}$
-name
![]() such that:
such that:
-
(a)
 $r(\vec {\nu }_0),r(\vec {\nu }_1)\leq q$
.
$r(\vec {\nu }_0),r(\vec {\nu }_1)\leq q$
. -
(b)
 .
. -
(c)

Then D is dense (open) above
![]() ${\langle } t_{<\kappa },t_\kappa {\rangle }$
and thus
${\langle } t_{<\kappa },t_\kappa {\rangle }$
and thus
![]() $D\cap G_\kappa *F_\kappa \neq \emptyset $
.
$D\cap G_\kappa *F_\kappa \neq \emptyset $
.
Proof Work in V, and let
![]() ${\langle } t_{<\kappa },t_\kappa {\rangle }\leq p:={\langle } p_{<\kappa },p_\kappa {\rangle } \in {\mathcal P}_{\kappa +1}$
. We will define two extensions
${\langle } t_{<\kappa },t_\kappa {\rangle }\leq p:={\langle } p_{<\kappa },p_\kappa {\rangle } \in {\mathcal P}_{\kappa +1}$
. We will define two extensions
![]() $p\leq q\leq q^*$
as before such that
$p\leq q\leq q^*$
as before such that
![]() $q^*\in D$
. By definition of
$q^*\in D$
. By definition of
![]() $\mathcal {P}_{\kappa +1}$
,
$\mathcal {P}_{\kappa +1}$
,
![]() $p_{<\kappa }\Vdash p_\kappa \in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})$
, by
$p_{<\kappa }\Vdash p_\kappa \in \operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^{++})$
, by
![]() $\kappa -$
cc of
$\kappa -$
cc of
![]() $\mathcal {P}_\kappa $
, for some
$\mathcal {P}_\kappa $
, for some
![]() $Z\subseteq \kappa ^{++},\ Z\in V$
,
$Z\subseteq \kappa ^{++},\ Z\in V$
,
![]() $|Z|<\kappa $
and some
$|Z|<\kappa $
and some
![]() $\gamma <\kappa $
,
$\gamma <\kappa $
,
![]() $p_{<\kappa }\Vdash \operatorname {\mathrm {dom}}(p_\kappa )\subseteq \gamma \times Z$
. The same argument as before indicates that
$p_{<\kappa }\Vdash \operatorname {\mathrm {dom}}(p_\kappa )\subseteq \gamma \times Z$
. The same argument as before indicates that
Denote
![]() $\mu =(j_2\restriction (Z\cup N_0))^{-1}\in M_2$
, then
$\mu =(j_2\restriction (Z\cup N_0))^{-1}\in M_2$
, then
and we can reformulate
Also, find
![]() $\delta <\kappa $
such that
$\delta <\kappa $
such that
![]() $t_{<\kappa }\Vdash \phi "(\delta ,\kappa )\cap Z=\emptyset .$
We have that
$t_{<\kappa }\Vdash \phi "(\delta ,\kappa )\cap Z=\emptyset .$
We have that
Therefore in
![]() $M_2$
we will have that
$M_2$
we will have that
Let
![]() $\Gamma $
be such that
$\Gamma $
be such that
![]() $j_2(\Gamma )(\vec {\xi })=\mu $
, and there is a set
$j_2(\Gamma )(\vec {\xi })=\mu $
, and there is a set
![]() $\overline {B}_0\subseteq B'$
,
$\overline {B}_0\subseteq B'$
,
![]() $\overline {B}_0\in E(\vec {\xi })$
such that for every
$\overline {B}_0\in E(\vec {\xi })$
such that for every
![]() $\vec {\nu }\in \overline {B}_0$
:
$\vec {\nu }\in \overline {B}_0$
:
Find
![]() $\vec {\nu }_0,\vec {\nu }_1\in \overline {B}_0$
such that
$\vec {\nu }_0,\vec {\nu }_1\in \overline {B}_0$
such that
![]() $r(\vec {\nu }_0),r(\vec {\nu }_1)$
are compatible,
$r(\vec {\nu }_0),r(\vec {\nu }_1)$
are compatible,
![]() $\vec {\nu }_0(0)>\delta ,\gamma ,\sup (\operatorname {\mathrm {Supp}}(p_{<\kappa }))$
, and
$\vec {\nu }_0(0)>\delta ,\gamma ,\sup (\operatorname {\mathrm {Supp}}(p_{<\kappa }))$
, and
![]() $\vec {\nu }_1(0)>\vec {\nu }_0(i_0),\sup (\operatorname {\mathrm {Supp}}(r_{<\kappa }(\vec {\nu }))$
. Denote
$\vec {\nu }_1(0)>\vec {\nu }_0(i_0),\sup (\operatorname {\mathrm {Supp}}(r_{<\kappa }(\vec {\nu }))$
. Denote
As before, q has the form:
![]() $q=p_{<\kappa }{}^{\smallfrown }q_{\vec {\nu }_0(0)}{}^{\smallfrown }r^0_{(\vec {\nu }_0(0),\kappa )}{}^{\smallfrown }q_\kappa $
. We have
$q=p_{<\kappa }{}^{\smallfrown }q_{\vec {\nu }_0(0)}{}^{\smallfrown }r^0_{(\vec {\nu }_0(0),\kappa )}{}^{\smallfrown }q_\kappa $
. We have
![]() $q_{\vec {\nu }_0(0)}$
is a
$q_{\vec {\nu }_0(0)}$
is a
![]() $\mathcal {P}_{\vec {\nu }_0(0)}$
-name for a condition with
$\mathcal {P}_{\vec {\nu }_0(0)}$
-name for a condition with
![]() $\operatorname {\mathrm {Supp}}(q_{\vec {\nu }_0(0)})= \Gamma (\vec {\nu }_0)"Z$
and
$\operatorname {\mathrm {Supp}}(q_{\vec {\nu }_0(0)})= \Gamma (\vec {\nu }_0)"Z$
and
![]() $q_{\nu ^{\prime }_0,\Gamma (\nu ^{\prime }_0,\nu _0)(\beta )}= p_{\kappa ,\beta }$
. As for
$q_{\nu ^{\prime }_0,\Gamma (\nu ^{\prime }_0,\nu _0)(\beta )}= p_{\kappa ,\beta }$
. As for
![]() $q_\kappa $
, we set it to be a
$q_\kappa $
, we set it to be a
![]() $\mathcal {P}_\kappa $
-name for
$\mathcal {P}_\kappa $
-name for
![]() $r^0_\kappa \cup p_\kappa $
.
$r^0_\kappa \cup p_\kappa $
.
The argument that
![]() $r^0\leq q$
is the same as in the case of
$r^0\leq q$
is the same as in the case of
![]() $\kappa ^+$
.
$\kappa ^+$
.
The choice of
![]() is possible since
is possible since
![]() $r^0\leq q$
and
$r^0\leq q$
and
![]() .
.
Define the final condition
![]() $q\leq q^*$
,
$q\leq q^*$
,
Again we have that
![]() $r^0\Vdash X_1^{\vec {\nu }_0(i_0)}\subseteq \phi "(\vec {\nu }_0(0),\vec {\nu }_0(i_0))\subseteq \phi "(\vec {\nu }_0(0),\vec {\nu }_1(0))$
and by
$r^0\Vdash X_1^{\vec {\nu }_0(i_0)}\subseteq \phi "(\vec {\nu }_0(0),\vec {\nu }_0(i_0))\subseteq \phi "(\vec {\nu }_0(0),\vec {\nu }_1(0))$
and by
![]() $(iii)$
$(iii)$
Now for the code of
, let
and

and
![]() $q^*_\kappa =q_\kappa \cup r^1_\kappa $
. We conclude that
$q^*_\kappa =q_\kappa \cup r^1_\kappa $
. We conclude that
![]() $r^0\leq q\leq q^*$
,
$r^0\leq q\leq q^*$
,
![]() $r^1\leq q^*$
, namely
$r^1\leq q^*$
, namely
![]() $(a)$
. Finally, for every
$(a)$
. Finally, for every
![]() $\tau \in X^{\vec {\nu }_0(i_0)}_1$
,
$\tau \in X^{\vec {\nu }_0(i_0)}_1$
,
and by
![]() $(3)_{(\vec {\nu }_1)}$
we have that
$(3)_{(\vec {\nu }_1)}$
we have that
![]() $q^*$
forces that
$q^*$
forces that
Then
![]() $p\leq q^*$
and
$p\leq q^*$
and
![]() $q^*\in D.$
$q^*\in D.$
The rest of the argument remains unchanged.
⊣
4 On the Extender-based Prikry forcings and adding subsets to
 $\kappa $
$\kappa $
H. Woodin asked in the early 90s whether, assuming that there is no inner model with a strong cardinal, it is possible to have a model M in which
![]() $2^{\aleph _\omega }\geq \aleph _{\omega +3}$
, GCH holds below
$2^{\aleph _\omega }\geq \aleph _{\omega +3}$
, GCH holds below
![]() $\aleph _\omega $
, there is an inner model N such that
$\aleph _\omega $
, there is an inner model N such that
![]() $\kappa =(\aleph _\omega )^M$
is a measurable and
$\kappa =(\aleph _\omega )^M$
is a measurable and
![]() $2^{\kappa }\geq (\aleph _{\omega +3})^M$
. His question was natural given the results known back then: Magidor [Reference Magidor26] proved that it is consistent relative to a supercompact cardinal and a huge cardinal above it to have
$2^{\kappa }\geq (\aleph _{\omega +3})^M$
. His question was natural given the results known back then: Magidor [Reference Magidor26] proved that it is consistent relative to a supercompact cardinal and a huge cardinal above it to have
![]() $2^{\aleph _\omega }\geq \aleph _{\omega +m}$
and
$2^{\aleph _\omega }\geq \aleph _{\omega +m}$
and
![]() $GCH_{<\aleph _\omega }$
using the supercompact Prikry forcing with collapses. Woodin, in an unpublished work which can be found in [Reference Cummings11] reduced Magidor’s large cardinal assumption to get
$GCH_{<\aleph _\omega }$
using the supercompact Prikry forcing with collapses. Woodin, in an unpublished work which can be found in [Reference Cummings11] reduced Magidor’s large cardinal assumption to get
![]() $2^{\aleph _{\omega }}=\aleph _{\omega +2}+GCH_<\aleph _{\omega }$
to a strong cardinal (actually to a
$2^{\aleph _{\omega }}=\aleph _{\omega +2}+GCH_<\aleph _{\omega }$
to a strong cardinal (actually to a
![]() $p_2\kappa $
-hypermeasurable). Later, Gitik and Magidor [Reference Gitik and Magidor21] proved using the Extender-based Prikry forcing with collapses that starting from the optimal large cardinal assumption, it is possible to obtain
$p_2\kappa $
-hypermeasurable). Later, Gitik and Magidor [Reference Gitik and Magidor21] proved using the Extender-based Prikry forcing with collapses that starting from the optimal large cardinal assumption, it is possible to obtain
![]() $\aleph _{\omega +m}=2^{\aleph _\omega }$
and
$\aleph _{\omega +m}=2^{\aleph _\omega }$
and
![]() $GCH_{<\aleph _\omega }$
. However, Woodin’s question remained unanswered.
$GCH_{<\aleph _\omega }$
. However, Woodin’s question remained unanswered.
A natural approach to answer Woodin’s question is to force with the Extender-based Prikry forcing over
![]() $\kappa $
and then argue that in some intermediate where
$\kappa $
and then argue that in some intermediate where
![]() $\kappa $
is measurable we added
$\kappa $
is measurable we added
![]() $\lambda \geq \kappa ^{++}$
many subsets to
$\lambda \geq \kappa ^{++}$
many subsets to
![]() $\kappa $
.
$\kappa $
.
Our purpose will be to show that this direction is doomed. More precisely, we will prove that in any intermediate model of the Extender-based Prikry forcing where
![]() $\kappa ^{++}$
-many subsets of
$\kappa ^{++}$
-many subsets of
![]() $\kappa $
were introduced,
$\kappa $
were introduced,
![]() $\kappa $
is singularized (and in particular not measurable). We will analyze the situation in both the original version of Gitik and Magidor from [Reference Gitik and Magidor21] and Merimovich version of the Extender-based Prikry forcing from [Reference Merimovich29–Reference Merimovich31]. We will rely on the following theorem from [Reference Benhamou and Gitik6, Theorem 6.7]:
$\kappa $
is singularized (and in particular not measurable). We will analyze the situation in both the original version of Gitik and Magidor from [Reference Gitik and Magidor21] and Merimovich version of the Extender-based Prikry forcing from [Reference Merimovich29–Reference Merimovich31]. We will rely on the following theorem from [Reference Benhamou and Gitik6, Theorem 6.7]:
Theorem 4.1. Suppose that
![]() $\mathbb {U}={\langle } U_a\mid a\in [\kappa ]^{<\omega }{\rangle }$
is a tree of P-point ultrafilters. Let
$\mathbb {U}={\langle } U_a\mid a\in [\kappa ]^{<\omega }{\rangle }$
is a tree of P-point ultrafilters. Let
![]() $G\subseteq P(\mathbb {U})$
be V-generic, then for every set of ordinals
$G\subseteq P(\mathbb {U})$
be V-generic, then for every set of ordinals
![]() $A\in V[G]\setminus V$
,
$A\in V[G]\setminus V$
,
![]() $cf^{V[A]}(\kappa )=\omega $
.
$cf^{V[A]}(\kappa )=\omega $
.
Note that if U is any
![]() $\kappa $
-complete ultrafilter, then the forcing
$\kappa $
-complete ultrafilter, then the forcing
![]() $\operatorname {\mathrm {Prikry}}(U)$
which we use in this paper is forcing equivalent to
$\operatorname {\mathrm {Prikry}}(U)$
which we use in this paper is forcing equivalent to
![]() $P(\mathbb {U})$
where
$P(\mathbb {U})$
where
![]() $\mathbb {U}={\langle } U_a\mid a\in [\kappa ]^{<\omega }{\rangle }$
is such that
$\mathbb {U}={\langle } U_a\mid a\in [\kappa ]^{<\omega }{\rangle }$
is such that
![]() $U_a=U$
for every a.
$U_a=U$
for every a.
Assume
![]() $2^{\kappa }=\kappa ^+$
. Let E be an extender over
$2^{\kappa }=\kappa ^+$
. Let E be an extender over
![]() $\kappa $
. We consider two sorts of Extender-based Prikry forcings—the original one (see [Reference Gitik and Magidor21] or [Reference Gitik, Foreman and Kanamori17]) and a more elegant version of Merimovich [Reference Merimovich29–Reference Merimovich31].
$\kappa $
. We consider two sorts of Extender-based Prikry forcings—the original one (see [Reference Gitik and Magidor21] or [Reference Gitik, Foreman and Kanamori17]) and a more elegant version of Merimovich [Reference Merimovich29–Reference Merimovich31].
Let us start with the Merimovich version, but in which the measures of E are P-points as in [Reference Gitik and Magidor21].
4.1 The Merimovich version with P-points
Suppose that there is
![]() $h:\kappa \to \kappa $
such that all the generators of E are below
$h:\kappa \to \kappa $
such that all the generators of E are below
![]() $j_E(h)(\kappa )$
.
$j_E(h)(\kappa )$
.
For example, if E is a
![]() $(\kappa , \kappa ^{++})$
-extender, this holds with
$(\kappa , \kappa ^{++})$
-extender, this holds with
![]() $h(\nu )=\nu ^{++}$
,
$h(\nu )=\nu ^{++}$
,
![]() $\nu <\kappa $
. This is sufficient to ensure that for every
$\nu <\kappa $
. This is sufficient to ensure that for every
![]() $\alpha <\lambda $
,
$\alpha <\lambda $
,
![]() $U_\alpha $
is a P-point ultrafilter.
$U_\alpha $
is a P-point ultrafilter.
Denote by
![]() $\mathbb {P}_E$
the Merimovich Extender-based Prikry forcing with E, as defined in [Reference Merimovich31] (or see Definition 1.5).
$\mathbb {P}_E$
the Merimovich Extender-based Prikry forcing with E, as defined in [Reference Merimovich31] (or see Definition 1.5).
Theorem 4.2. Let
![]() $G\subseteq \mathbb {P}_E$
be a generic. Suppose that
$G\subseteq \mathbb {P}_E$
be a generic. Suppose that
![]() $A\in V[G]\setminus V$
is a subset of
$A\in V[G]\setminus V$
is a subset of
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $\kappa $
changes its cofinality to
$\kappa $
changes its cofinality to
![]() $\omega $
in
$\omega $
in
![]() $V[A]$
.
$V[A]$
.
Proof Work in V. Suppose that
![]() is a name of a subset of
is a name of a subset of
![]() $\kappa $
and some
$\kappa $
and some
![]() $p\in \mathbb {P}_E$
forces that it is a new subset.
$p\in \mathbb {P}_E$
forces that it is a new subset.
Let us use
![]() $\kappa ^+$
-properness of the forcing
$\kappa ^+$
-properness of the forcing
![]() $\mathbb {P}_E$
(see [Reference Merimovich31, Claim 2.7] or [Reference Merimovich29, Claim 3.29]). Pick now
$\mathbb {P}_E$
(see [Reference Merimovich31, Claim 2.7] or [Reference Merimovich29, Claim 3.29]). Pick now
![]() $N\preceq H_\chi $
, for some
$N\preceq H_\chi $
, for some
![]() $\chi $
large enough such that:
$\chi $
large enough such that:
-
(1)
 $|N|=\kappa $
,
$|N|=\kappa $
, -
(2)
 $N\supseteq {}^{\kappa>}N$
,
$N\supseteq {}^{\kappa>}N$
, -
(3)
 .
.
The properness implies that there is
![]() $p^*\geq ^* p$
which is
$p^*\geq ^* p$
which is
![]() ${\langle } N, \mathbb {P}_E{\rangle }$
-generic, i.e.,
${\langle } N, \mathbb {P}_E{\rangle }$
-generic, i.e.,
In particular, for every
![]() $\nu <\kappa $
, the dense open set
$\nu <\kappa $
, the dense open set
is definable from
and
![]() $\nu $
, hence in N and it is dense open by elementarity.
$\nu $
, hence in N and it is dense open by elementarity.
Consider
![]() $X=\cup _{p\in \mathbb {P}_E\cap N}\operatorname {\mathrm {Supp}}(p)$
, since
$X=\cup _{p\in \mathbb {P}_E\cap N}\operatorname {\mathrm {Supp}}(p)$
, since
![]() $\operatorname {\mathrm {Supp}}(p),N$
are of size
$\operatorname {\mathrm {Supp}}(p),N$
are of size
![]() $\kappa $
, and we have that
$\kappa $
, and we have that
![]() $|X|\leq \kappa $
. There exists
$|X|\leq \kappa $
. There exists
![]() $\alpha ^*<\lambda $
such that for some
$\alpha ^*<\lambda $
such that for some
![]() $f\in V$
,
$f\in V$
,
![]() $j_E(f)(\alpha ^*)=(j\restriction X)^{-1}$
(see, for example, [Reference Gitik, Foreman and Kanamori17, Lemma 3.3]).
$j_E(f)(\alpha ^*)=(j\restriction X)^{-1}$
(see, for example, [Reference Gitik, Foreman and Kanamori17, Lemma 3.3]).
Denote
![]() $Y=X\cup \{\alpha ^*\}$
and fix a set
$Y=X\cup \{\alpha ^*\}$
and fix a set
![]() $R\in E_{Y}$
such that if
$R\in E_{Y}$
such that if
![]() $\mu \in R$
, then
$\mu \in R$
, then
![]() $f(\mu (\alpha ^*))=\mu \restriction X$
. Such a set exists since
$f(\mu (\alpha ^*))=\mu \restriction X$
. Such a set exists since
![]() $j_E(f)(j^{-1}(j(\alpha ^*)))=(j\restriction X)^{-1}$
, hence
$j_E(f)(j^{-1}(j(\alpha ^*)))=(j\restriction X)^{-1}$
, hence
Find a condition
![]() $p_*\in G$
such that
$p_*\in G$
such that
![]() $Y\subseteq \operatorname {\mathrm {Supp}}(p)$
and
$Y\subseteq \operatorname {\mathrm {Supp}}(p)$
and
![]() $A^{p_*}\restriction Y\subseteq R$
. Define
$A^{p_*}\restriction Y\subseteq R$
. Define
![]() $G\restriction Y=\{p\restriction Y \mid p\in G/p_*\}$
. Then by genericity of
$G\restriction Y=\{p\restriction Y \mid p\in G/p_*\}$
. Then by genericity of
![]() $p^*$
and definition of Y, for every
$p^*$
and definition of Y, for every
![]() $\alpha <\kappa $
there is
$\alpha <\kappa $
there is
![]() $p_\alpha \in G\cap D_\nu \cap N$
, hence
$p_\alpha \in G\cap D_\nu \cap N$
, hence
![]() $\operatorname {\mathrm {Supp}}(p_\alpha )\subseteq Y$
and we can find
$\operatorname {\mathrm {Supp}}(p_\alpha )\subseteq Y$
and we can find
![]() $p_\alpha \leq p^*_\alpha \in G\restriction Y\cap D_\nu $
. It follows that
$p_\alpha \leq p^*_\alpha \in G\restriction Y\cap D_\nu $
. It follows that
![]() $A\in V[G\restriction Y]$
. Let
$A\in V[G\restriction Y]$
. Let
![]() $G_{\alpha ^*}=\{p\restriction \{\alpha ^*\}\mid p\in G/p_*\}$
, in particular,
$G_{\alpha ^*}=\{p\restriction \{\alpha ^*\}\mid p\in G/p_*\}$
, in particular,
![]() $p_0:=p_*\restriction \{\alpha ^*\}\in G_{\alpha ^*}$
. Note that
$p_0:=p_*\restriction \{\alpha ^*\}\in G_{\alpha ^*}$
. Note that
![]() $G_{\alpha ^*}$
is essentially a Prikry generic filter for
$G_{\alpha ^*}$
is essentially a Prikry generic filter for
![]() $\operatorname {\mathrm {Prikry}}(U_{\alpha ^*}).$
$\operatorname {\mathrm {Prikry}}(U_{\alpha ^*}).$
Claim 4.3.
![]() $V[G\restriction Y]=V[G_{\alpha ^*}]$
.
$V[G\restriction Y]=V[G_{\alpha ^*}]$
.
Proof Inclusion from right to left is clear as
![]() $\alpha ^*\in Y$
. For the other direction, let
$\alpha ^*\in Y$
. For the other direction, let
![]() $p_0={\langle } t_0,B_0{\rangle }\leq q={\langle } t, B{\rangle }\in G_{\alpha ^*}$
. For every
$p_0={\langle } t_0,B_0{\rangle }\leq q={\langle } t, B{\rangle }\in G_{\alpha ^*}$
. For every
![]() $|t_0|<i\leq |t| \ t(i)\in B\subseteq B_0$
, by the property of R, we have that
$|t_0|<i\leq |t| \ t(i)\in B\subseteq B_0$
, by the property of R, we have that
![]() $\mu _i:=f(t(i))\smallfrown t(i)\in A^{p^*}$
such that
$\mu _i:=f(t(i))\smallfrown t(i)\in A^{p^*}$
such that
![]() $\mu _i(\alpha ^*)=t(i)$
. Now define
$\mu _i(\alpha ^*)=t(i)$
. Now define
![]() $q'={\langle } f,B'{\rangle }$
as follows:
$q'={\langle } f,B'{\rangle }$
as follows:
![]() $\operatorname {\mathrm {dom}}(f)=Y$
and
$\operatorname {\mathrm {dom}}(f)=Y$
and
In particular
![]() $f(\alpha ^*)=t\geq f^{p_*}(\alpha ^*)$
. Also, let
$f(\alpha ^*)=t\geq f^{p_*}(\alpha ^*)$
. Also, let
![]() $B'=\{\mu \mid \mu (\alpha ^*)\in B', \ f(\mu (\alpha ^*))=\mu \restriction X\}$
. We claim that
$B'=\{\mu \mid \mu (\alpha ^*)\in B', \ f(\mu (\alpha ^*))=\mu \restriction X\}$
. We claim that
![]() $G\restriction Y=\{q'\mid q\in G_{\alpha ^*}/p_0\}$
. Indeed if
$G\restriction Y=\{q'\mid q\in G_{\alpha ^*}/p_0\}$
. Indeed if
![]() $p\in G/p_*$
then
$p\in G/p_*$
then
![]() $q=p\restriction \{\alpha ^*\}\in G_{\alpha ^*}$
and it is straightforward to check that
$q=p\restriction \{\alpha ^*\}\in G_{\alpha ^*}$
and it is straightforward to check that
![]() $q'=p\restriction Y$
. It follows that
$q'=p\restriction Y$
. It follows that
![]() $G\restriction Y$
is definable in
$G\restriction Y$
is definable in
![]() $V[G_{\alpha ^*}]$
.
$V[G_{\alpha ^*}]$
.
By our assumption
![]() $U_{\alpha ^*}$
is a P-point ultrafilter. Now, Theorem 4.1 applies, so
$U_{\alpha ^*}$
is a P-point ultrafilter. Now, Theorem 4.1 applies, so
4.2 The original version
The difference here from the forcing of the previous section is that the order
![]() $\leq ^*$
is not
$\leq ^*$
is not
![]() $\kappa ^+$
-closed. However, we will show that the forcing is still
$\kappa ^+$
-closed. However, we will show that the forcing is still
![]() $\kappa ^+$
-proper.
$\kappa ^+$
-proper.
Assume for simplicity that E is a
![]() $(\kappa , \kappa ^{++})$
-extender and the function
$(\kappa , \kappa ^{++})$
-extender and the function
![]() $\nu \mapsto \nu ^{++}$
represents
$\nu \mapsto \nu ^{++}$
represents
![]() $\kappa ^{++}$
in the ultrapower.
$\kappa ^{++}$
in the ultrapower.
Let
![]() ${\mathcal P}_E$
be the forcing of [Reference Gitik and Magidor21] with E.
${\mathcal P}_E$
be the forcing of [Reference Gitik and Magidor21] with E.
Lemma 4.4. Assume
![]() $p\in {\mathcal P}_E$
. Let
$p\in {\mathcal P}_E$
. Let
![]() $N\preceq H_\chi $
, for some
$N\preceq H_\chi $
, for some
![]() $\chi $
large enough such that:
$\chi $
large enough such that:
-
(1)
 $|N|=\kappa $
,
$|N|=\kappa $
, -
(2)
 $N\supseteq {}^{\kappa>}N$
,
$N\supseteq {}^{\kappa>}N$
, -
(3)
 $E, {\mathcal P}_E, p \in N$
.
$E, {\mathcal P}_E, p \in N$
.
Then there is
![]() $p^*\geq p$
which is
$p^*\geq p$
which is
![]() ${\langle } N, {\mathcal P}_E{\rangle }$
-generic.
${\langle } N, {\mathcal P}_E{\rangle }$
-generic.
Proof Let
![]() ${\langle } D_\nu \mid \nu <\kappa {\rangle }$
be an enumeration of all dense open subsets of
${\langle } D_\nu \mid \nu <\kappa {\rangle }$
be an enumeration of all dense open subsets of
![]() ${\mathcal P}_E$
which are in N. Proceed by induction and define a
${\mathcal P}_E$
which are in N. Proceed by induction and define a
![]() $\leq ^*$
-increasing sequence
$\leq ^*$
-increasing sequence
![]() ${\langle } p_\nu \mid \nu <\kappa {\rangle }$
of extensions of p such that, for every
${\langle } p_\nu \mid \nu <\kappa {\rangle }$
of extensions of p such that, for every
![]() $\nu <\kappa $
:
$\nu <\kappa $
:
-
(a)
 $p_\nu \in N$
.
$p_\nu \in N$
. -
(b)
 $\min (A_\nu ^0)>\nu $
, where
$\min (A_\nu ^0)>\nu $
, where
 $A_\nu ^0=\{\rho ^0\mid \rho \in A_\nu \}$
is the projection of
$A_\nu ^0=\{\rho ^0\mid \rho \in A_\nu \}$
is the projection of
 $A_\nu $
to the normal measure.
$A_\nu $
to the normal measure. -
(c) There is
 $k<\omega $
such that for every
$k<\omega $
such that for every
 ${\langle } \rho _1,..., \rho _k{\rangle } \in [A_\nu ]^k$
,
${\langle } \rho _1,..., \rho _k{\rangle } \in [A_\nu ]^k$
,
 $p_\nu {}^\frown {\langle } \rho _1,..., \rho _k{\rangle } \in D_\nu $
.
$p_\nu {}^\frown {\langle } \rho _1,..., \rho _k{\rangle } \in D_\nu $
.
It is natural now to move now to a coordinate
![]() $\eta $
which is above everything in N and to take the diagonal intersection
$\eta $
which is above everything in N and to take the diagonal intersection
![]() $\Delta ^*$
of the pre-images of
$\Delta ^*$
of the pre-images of
![]() $A_\nu $
’s according to the normal measure. However, in order to have the property (c) above, something more is needed. Namely, we would like to have the following:
$A_\nu $
’s according to the normal measure. However, in order to have the property (c) above, something more is needed. Namely, we would like to have the following:
-
(d) for every
 ${\langle } \xi _1, ..., \xi _m{\rangle } \in [\min (A_\nu ^0)]^{<\omega }$
, if
${\langle } \xi _1, ..., \xi _m{\rangle } \in [\min (A_\nu ^0)]^{<\omega }$
, if
 $p_\nu {}^\frown {\langle } \xi _1, ..., \xi _m{\rangle }\in {\mathcal P}_E$
then there is
$p_\nu {}^\frown {\langle } \xi _1, ..., \xi _m{\rangle }\in {\mathcal P}_E$
then there is
 $k<\omega $
such that:
$k<\omega $
such that:  $$ \begin{align*}\text{for every }{\langle} \rho_1,..., \rho_k{\rangle} \in [A_\nu]^k, \ p_\nu{}^\frown {\langle} \xi_1, ..., \xi_m{\rangle}^\frown {\langle} \rho_1,..., \rho_k{\rangle} \in D_\nu.\end{align*} $$
$$ \begin{align*}\text{for every }{\langle} \rho_1,..., \rho_k{\rangle} \in [A_\nu]^k, \ p_\nu{}^\frown {\langle} \xi_1, ..., \xi_m{\rangle}^\frown {\langle} \rho_1,..., \rho_k{\rangle} \in D_\nu.\end{align*} $$
Given (d), as we will see, the idea above works fine. Let us construct a sequence which satisfies the conditions (a)–(d).
Pick
![]() $p_0\in N$
such that
$p_0\in N$
such that
![]() $p_0\geq ^* p$
and (d) is satisfied. To define
$p_0\geq ^* p$
and (d) is satisfied. To define
![]() $p_1$
, use the strong Prikry property to pick a condition
$p_1$
, use the strong Prikry property to pick a condition
![]() $p_1^{\prime } \in N$
,
$p_1^{\prime } \in N$
,
![]() $p_1^{\prime }\geq ^*p_0$
and
$p_1^{\prime }\geq ^*p_0$
and
Let
![]() $\eta _0=\min ((A_1^{\prime })^0)$
, by definition of
$\eta _0=\min ((A_1^{\prime })^0)$
, by definition of
![]() $\pi _{\alpha ,\kappa }$
it follows that
$\pi _{\alpha ,\kappa }$
it follows that
![]() $\eta _0$
is an inaccessible cardinal.
$\eta _0$
is an inaccessible cardinal.
Let
![]() ${\langle } \vec {\xi }_i \mid i<\eta _0{\rangle } $
be an enumeration of
${\langle } \vec {\xi }_i \mid i<\eta _0{\rangle } $
be an enumeration of
![]() $[\eta _0]^{<\omega }$
.
$[\eta _0]^{<\omega }$
.
Define
![]() $\leq ^*$
-increasing sequence
$\leq ^*$
-increasing sequence
![]() ${\langle } q_i\mid i<\eta _0{\rangle }$
.
${\langle } q_i\mid i<\eta _0{\rangle }$
.
Consider
![]() $p_1^{\prime }{}^\frown \vec {\xi }_0$
. If it does not extend
$p_1^{\prime }{}^\frown \vec {\xi }_0$
. If it does not extend
![]() $p_0$
, then set
$p_0$
, then set
![]() $q_0=p_1^{\prime }$
. Otherwise, pick (inside N)
$q_0=p_1^{\prime }$
. Otherwise, pick (inside N)
![]() $r_0\geq ^* p_1^{\prime }{}^\frown \vec {\xi }_0$
such that
$r_0\geq ^* p_1^{\prime }{}^\frown \vec {\xi }_0$
such that
Let
![]() $q_0={\langle } f^{q_0},A^{q_0}{\rangle }$
be obtained from
$q_0={\langle } f^{q_0},A^{q_0}{\rangle }$
be obtained from
![]() $r_0$
by removing
$r_0$
by removing
![]() $\vec {\xi }_0$
from all coordinates which appear in
$\vec {\xi }_0$
from all coordinates which appear in
![]() $p_1^{\prime }$
(and leaving at new ones), and then, adding a larger maximal coordinate. Namely,
$p_1^{\prime }$
(and leaving at new ones), and then, adding a larger maximal coordinate. Namely,
![]() $\operatorname {\mathrm {dom}}(f^{q_0})=\operatorname {\mathrm {dom}}(f^{r_0})\cup \{\alpha _0\}$
where
$\operatorname {\mathrm {dom}}(f^{q_0})=\operatorname {\mathrm {dom}}(f^{r_0})\cup \{\alpha _0\}$
where
![]() $\alpha _0$
is
$\alpha _0$
is
![]() $\leq _E$
strictly above all the ordinals in
$\leq _E$
strictly above all the ordinals in
![]() $\operatorname {\mathrm {dom}}(f^{r_0})$
. Let t be such that
$\operatorname {\mathrm {dom}}(f^{r_0})$
. Let t be such that
![]() $\pi _{\alpha ,\kappa }"t=f^{p^{\prime }_1}(\kappa )$
and for every
$\pi _{\alpha ,\kappa }"t=f^{p^{\prime }_1}(\kappa )$
and for every
![]() $\gamma \in \operatorname {\mathrm {dom}}(f^{q_0}),$
$\gamma \in \operatorname {\mathrm {dom}}(f^{q_0}),$
 $$ \begin{align*}f^{q_0}(\gamma)=\begin{cases}f^{p^{\prime}_1}(\gamma), & \gamma\in Supp(p^{\prime}_1),\\ f^{r_0}(\gamma), &\gamma\in Supp(r_0)\setminus Supp(p^{\prime}_1),\\ t, & \gamma=\alpha_0.\end{cases}\end{align*} $$
$$ \begin{align*}f^{q_0}(\gamma)=\begin{cases}f^{p^{\prime}_1}(\gamma), & \gamma\in Supp(p^{\prime}_1),\\ f^{r_0}(\gamma), &\gamma\in Supp(r_0)\setminus Supp(p^{\prime}_1),\\ t, & \gamma=\alpha_0.\end{cases}\end{align*} $$
Let
![]() $A^{q_0}=\pi _{\alpha _0,mc(r_0)}^{-1}[A^{r_0}]$
. Then
$A^{q_0}=\pi _{\alpha _0,mc(r_0)}^{-1}[A^{r_0}]$
. Then
![]() $q_0\in N$
and also
$q_0\in N$
and also
![]() $q_0\in {\mathcal P}_E$
. By shrinking
$q_0\in {\mathcal P}_E$
. By shrinking
![]() $A^{q_0}$
a bit more (as in [Reference Gitik, Foreman and Kanamori17, Lemma 3.10]) we secure condition (6), and
$A^{q_0}$
a bit more (as in [Reference Gitik, Foreman and Kanamori17, Lemma 3.10]) we secure condition (6), and
![]() $p_1^{\prime }\leq ^* q_0$
.
$p_1^{\prime }\leq ^* q_0$
.
Define
![]() $q_1$
in the exact same fashion only replacing
$q_1$
in the exact same fashion only replacing
![]() $p_1^{\prime }$
by
$p_1^{\prime }$
by
![]() $q_0$
and
$q_0$
and
![]() $\vec {\xi }_0$
by
$\vec {\xi }_0$
by
![]() $\vec {\xi }_1$
.
$\vec {\xi }_1$
.
Continue similarly for every
![]() $i<\eta _0$
, and finally, let
$i<\eta _0$
, and finally, let
![]() $q_{\eta _0}$
be a
$q_{\eta _0}$
be a
![]() $\leq ^*$
-extension of all
$\leq ^*$
-extension of all
![]() $q_i$
’s.
$q_i$
’s.
If
![]() $\eta _0=\min ((A(q_{\eta _0}))^0)$
, then set
$\eta _0=\min ((A(q_{\eta _0}))^0)$
, then set
![]() $p_1=q_{\eta _0}$
. Otherwise, let
$p_1=q_{\eta _0}$
. Otherwise, let
![]() $\eta _1=\min ((A(q_{\eta _0}))^0)$
. Repeat the process above with
$\eta _1=\min ((A(q_{\eta _0}))^0)$
. Repeat the process above with
![]() $\eta _1$
replacing
$\eta _1$
replacing
![]() $\eta _0$
and
$\eta _0$
and
![]() $q_{\eta _0}$
replacing
$q_{\eta _0}$
replacing
![]() $p_1^{\prime }$
. Continuing in a similar fashion, we hope to reach some
$p_1^{\prime }$
. Continuing in a similar fashion, we hope to reach some
![]() $\eta $
which is a fixed point, i.e.,
$\eta $
which is a fixed point, i.e.,
![]() $\eta =\min ((A(q_{\eta }))^0)$
. However, we need to do this a bit more carefully at limit stages. Let us pick an elementary substructure
$\eta =\min ((A(q_{\eta }))^0)$
. However, we need to do this a bit more carefully at limit stages. Let us pick an elementary substructure
![]() $N'\prec V_{\mu }$
for sufficiently large
$N'\prec V_{\mu }$
for sufficiently large
![]() $\mu $
of cardinality
$\mu $
of cardinality
![]() $\kappa ^+$
, closed under
$\kappa ^+$
, closed under
![]() $\kappa $
-sequences, including
$\kappa $
-sequences, including
![]() $p_1^{\prime },p_0,{\mathcal P}_E,E,...$
. We can find some
$p_1^{\prime },p_0,{\mathcal P}_E,E,...$
. We can find some
![]() $\alpha <\kappa ^{++}$
such that for every
$\alpha <\kappa ^{++}$
such that for every
![]() $p\in N'\cap {\mathcal P}_E$
and every
$p\in N'\cap {\mathcal P}_E$
and every
![]() $\gamma \in \operatorname {\mathrm {Supp}}(p)$
,
$\gamma \in \operatorname {\mathrm {Supp}}(p)$
,
![]() $\gamma <_E\alpha $
. Define a sequence of condition
$\gamma <_E\alpha $
. Define a sequence of condition
![]() ${\langle } q_{\eta _i}\mid i<\eta {\rangle }$
of conditions of
${\langle } q_{\eta _i}\mid i<\eta {\rangle }$
of conditions of
![]() $N'$
.
$N'$
.
We start with
![]() $q_{\eta _0}$
which is already defined. Let
$q_{\eta _0}$
which is already defined. Let
![]() $Y_0\in U_\alpha $
such that the commutativity requirement from Definition 1.6(6) holds with respect to
$Y_0\in U_\alpha $
such that the commutativity requirement from Definition 1.6(6) holds with respect to
![]() $\operatorname {\mathrm {Supp}}(q_{\eta _0})$
. If
$\operatorname {\mathrm {Supp}}(q_{\eta _0})$
. If
![]() $\eta _0=\min (Y_0^0)$
we are done. Otherwise, let
$\eta _0=\min (Y_0^0)$
we are done. Otherwise, let
![]() $\eta _1=\min (Y_0^0)$
and construct
$\eta _1=\min (Y_0^0)$
and construct
![]() $q_{\eta _1}$
in a similar fashion going over all possible
$q_{\eta _1}$
in a similar fashion going over all possible
![]() $\vec {\xi }\in [\eta _1]^{<\omega }$
, and construct
$\vec {\xi }\in [\eta _1]^{<\omega }$
, and construct
![]() $Y_1\in U_\alpha $
to satisfy (6) with respect to
$Y_1\in U_\alpha $
to satisfy (6) with respect to
![]() $\operatorname {\mathrm {Supp}}(q_{\eta _1})$
. At a general successor step, we are given
$\operatorname {\mathrm {Supp}}(q_{\eta _1})$
. At a general successor step, we are given
![]() $\eta _i, q_{\eta _i}$
, and
$\eta _i, q_{\eta _i}$
, and
![]() $Y_i$
. Check if
$Y_i$
. Check if
![]() $\eta _i=\min (Y_i^0)$
, if yes, stop the construction, set
$\eta _i=\min (Y_i^0)$
, if yes, stop the construction, set
![]() $p_1=q_{\eta _i}$
, and we are done. Otherwise, let
$p_1=q_{\eta _i}$
, and we are done. Otherwise, let
![]() $\eta _{i+1}=\min (Y^0_{i})$
, construct
$\eta _{i+1}=\min (Y^0_{i})$
, construct
![]() $q_{\eta _{i+1}}$
above
$q_{\eta _{i+1}}$
above
![]() $q_{\eta _i}$
as we did with
$q_{\eta _i}$
as we did with
![]() $q_{\eta _0}$
, going over all possible
$q_{\eta _0}$
, going over all possible
![]() $\vec {\xi }\in [\eta _{i+1}]^{<\omega }$
, then find
$\vec {\xi }\in [\eta _{i+1}]^{<\omega }$
, then find
![]() $Y_{i+1}\in U_\alpha $
satisfying (6) with respect to
$Y_{i+1}\in U_\alpha $
satisfying (6) with respect to
![]() $\operatorname {\mathrm {Supp}}(q_{\eta _{i+1}})$
. At limit stages
$\operatorname {\mathrm {Supp}}(q_{\eta _{i+1}})$
. At limit stages
![]() $\delta $
take
$\delta $
take
![]() $\eta _\delta =\sup _{i<\delta }\eta _i$
, check if
$\eta _\delta =\sup _{i<\delta }\eta _i$
, check if
![]() $\eta _\delta =\min ((\cap _{i<\delta }Y_i)^0)$
, if yes, stop the construction and consider the condition
$\eta _\delta =\min ((\cap _{i<\delta }Y_i)^0)$
, if yes, stop the construction and consider the condition
![]() $p_1=q_{\eta _\delta }$
with maximal coordinate
$p_1=q_{\eta _\delta }$
with maximal coordinate
![]() $\alpha $
, putting
$\alpha $
, putting
![]() $\cap _{i<\delta }Y_i$
as his measure one set. Then
$\cap _{i<\delta }Y_i$
as his measure one set. Then
![]() $q_{\eta _\delta }$
will be as desired. Otherwise, we find any
$q_{\eta _\delta }$
will be as desired. Otherwise, we find any
![]() $q_{\eta _\delta }\in N'$
above all the previous
$q_{\eta _\delta }\in N'$
above all the previous
![]() $q_{\eta _i}$
, and construct
$q_{\eta _i}$
, and construct
![]() $Y_{\delta }\in U_\alpha $
with respect to
$Y_{\delta }\in U_\alpha $
with respect to
![]() $\operatorname {\mathrm {Supp}}(q_{\eta _\delta })$
. We can further require that
$\operatorname {\mathrm {Supp}}(q_{\eta _\delta })$
. We can further require that
![]() $\pi _{\alpha ,mc(q_{\eta _i})}^{\prime \prime } Y_i\subseteq A(q_{\eta _i})$
and that
$\pi _{\alpha ,mc(q_{\eta _i})}^{\prime \prime } Y_i\subseteq A(q_{\eta _i})$
and that
![]() $\min (A(q_{\eta _i})^0)>i$
.
$\min (A(q_{\eta _i})^0)>i$
.
Assume toward a contradiction that no suitable
![]() $q_{\eta _\delta }$
was found and that the process goes all the way up to
$q_{\eta _\delta }$
was found and that the process goes all the way up to
![]() $\kappa $
. Consider
$\kappa $
. Consider
![]() $Y^*=\Delta _{i<\kappa }^*Y_i\in U_\alpha $
and let
$Y^*=\Delta _{i<\kappa }^*Y_i\in U_\alpha $
and let
![]() $\mu $
be any limit point of
$\mu $
be any limit point of
![]() $Y^*$
. Consider step
$Y^*$
. Consider step
![]() $\mu ^0$
of the construction, and we have
$\mu ^0$
of the construction, and we have
![]() $\eta _{\mu ^0}=\sup _{i<\mu ^0}\eta _i$
. For every
$\eta _{\mu ^0}=\sup _{i<\mu ^0}\eta _i$
. For every
![]() $i<\mu ^0$
, we have that
$i<\mu ^0$
, we have that
![]() $\mu \in Y_i$
, hence
$\mu \in Y_i$
, hence
![]() $\mu \in \cap _{i<\mu ^0}Y_i$
and
$\mu \in \cap _{i<\mu ^0}Y_i$
and
![]() $\mu ^0\in (\cap _{i<\mu ^0}Y_i)^0$
, and it follows that
$\mu ^0\in (\cap _{i<\mu ^0}Y_i)^0$
, and it follows that
![]() $\eta _{\mu ^0}\geq \mu ^0\geq \min ((\cap _{i<\mu ^0}Y_i)^0)\geq \eta _{\mu ^0}$
. This means that
$\eta _{\mu ^0}\geq \mu ^0\geq \min ((\cap _{i<\mu ^0}Y_i)^0)\geq \eta _{\mu ^0}$
. This means that
![]() $\eta _{\mu ^0}=\mu ^0=\min ((\cap _{i<\mu ^0}Y_i)^0)$
which indicates that the construction should have terminated at step
$\eta _{\mu ^0}=\mu ^0=\min ((\cap _{i<\mu ^0}Y_i)^0)$
which indicates that the construction should have terminated at step
![]() $\mu _0$
, contradiction.
$\mu _0$
, contradiction.
We conclude that
![]() $p_1$
is defined. The further construction of
$p_1$
is defined. The further construction of
![]() $p_\nu $
’s is similar, exploiting the
$p_\nu $
’s is similar, exploiting the
![]() $\kappa $
-closure of
$\kappa $
-closure of
![]() $\leq ^*$
.
$\leq ^*$
.
Pick now some
![]() $\alpha \geq _E \beta ,$
for every
$\alpha \geq _E \beta ,$
for every
![]() $\beta \in N\cap \operatorname {\mathrm {dom}}(E)$
which exists since
$\beta \in N\cap \operatorname {\mathrm {dom}}(E)$
which exists since
![]() $|N|=\kappa $
. Set
$|N|=\kappa $
. Set
where
![]() $\tilde {A}(p_\nu )$
is the pre-image of
$\tilde {A}(p_\nu )$
is the pre-image of
![]() ${A}(p_\nu )$
under the projection from
${A}(p_\nu )$
under the projection from
![]() $\alpha $
to
$\alpha $
to
![]() $mc(p_\nu )$
. Define a condition
$mc(p_\nu )$
. Define a condition
![]() $p^*={\langle } f^*,A^*{\rangle }$
from the sequence
$p^*={\langle } f^*,A^*{\rangle }$
from the sequence
![]() ${\langle } p_\nu \mid \nu <\kappa {\rangle }$
as follows:
${\langle } p_\nu \mid \nu <\kappa {\rangle }$
as follows:
![]() $\operatorname {\mathrm {Supp}}(p^*)=\cup _{\nu <\kappa }\operatorname {\mathrm {Supp}}(p_\nu )\cup \{\alpha \}$
, from the way we defined
$\operatorname {\mathrm {Supp}}(p^*)=\cup _{\nu <\kappa }\operatorname {\mathrm {Supp}}(p_\nu )\cup \{\alpha \}$
, from the way we defined
![]() $p_\nu $
there is no problem defining
$p_\nu $
there is no problem defining
![]() $f^*=\cup _{\nu <\kappa }f^{p_\nu }\cup \{{\langle }\alpha ,t{\rangle }\}$
where t is any sequence such that
$f^*=\cup _{\nu <\kappa }f^{p_\nu }\cup \{{\langle }\alpha ,t{\rangle }\}$
where t is any sequence such that
![]() $\pi _{\alpha ,\kappa }^{\prime \prime }t=f^*(\kappa )$
. Then we take
$\pi _{\alpha ,\kappa }^{\prime \prime }t=f^*(\kappa )$
. Then we take
![]() $A^*=A$
. It follows that
$A^*=A$
. It follows that
![]() $p^*\in {\mathcal P}_E$
, and it has the property that for every
$p^*\in {\mathcal P}_E$
, and it has the property that for every
![]() $\nu <\kappa $
and any sequence
$\nu <\kappa $
and any sequence
of ordinals from A,
![]() $p_\nu ^{\smallfrown }{\langle }\xi _1,...,\xi _n{\rangle }\leq p^*{}^{\smallfrown }{\langle } \xi _1,...,\xi _n{\rangle }$
.Footnote
8
Let us argue that it is
$p_\nu ^{\smallfrown }{\langle }\xi _1,...,\xi _n{\rangle }\leq p^*{}^{\smallfrown }{\langle } \xi _1,...,\xi _n{\rangle }$
.Footnote
8
Let us argue that it is
![]() ${\langle } N,{\mathcal P}_E{\rangle }$
-generic. Let G be generic with
${\langle } N,{\mathcal P}_E{\rangle }$
-generic. Let G be generic with
![]() $p^*\in G$
. We need to prove that
$p^*\in G$
. We need to prove that
![]() $G\cap N\cap D_\nu \neq \emptyset $
for every
$G\cap N\cap D_\nu \neq \emptyset $
for every
![]() $\nu <\kappa $
. By density, pick any
$\nu <\kappa $
. By density, pick any
![]() $p^{\smallfrown }{\langle }\xi _1,...,\xi _{k_1}{\rangle }\leq ^*q\in D_\nu \cap G$
, and let m be such that
$p^{\smallfrown }{\langle }\xi _1,...,\xi _{k_1}{\rangle }\leq ^*q\in D_\nu \cap G$
, and let m be such that
![]() $\xi _1,...,\xi _m<\min (A(p_\nu ))\leq \xi _{m+1}<\cdots <\xi _{k_1}$
. By condition (d), there is
$\xi _1,...,\xi _m<\min (A(p_\nu ))\leq \xi _{m+1}<\cdots <\xi _{k_1}$
. By condition (d), there is
![]() $k_2$
such that any
$k_2$
such that any
![]() ${\langle }\nu _1,...,\nu _{k_2}{\rangle }\in [A_\nu ]^{k_2}$
extension
${\langle }\nu _1,...,\nu _{k_2}{\rangle }\in [A_\nu ]^{k_2}$
extension
![]() $p_\nu ^{\smallfrown }{\langle }\xi _1,...,\xi _m{\rangle }^{\smallfrown }{\langle } \nu _1,...,\nu _{k_2}{\rangle }\in D_\nu $
. If necessary, extend q to
$p_\nu ^{\smallfrown }{\langle }\xi _1,...,\xi _m{\rangle }^{\smallfrown }{\langle } \nu _1,...,\nu _{k_2}{\rangle }\in D_\nu $
. If necessary, extend q to
and suppose without loss of generality that
![]() $k_1\geq m+k_2$
. Since
$k_1\geq m+k_2$
. Since
![]() $\nu <\min (A(p_\nu )^0)\leq \xi _{m+1}$
, by definition of
$\nu <\min (A(p_\nu )^0)\leq \xi _{m+1}$
, by definition of
![]() $\pi _{\alpha ,\kappa }$
, it follows that
$\pi _{\alpha ,\kappa }$
, it follows that
![]() $\nu <\xi _{m+1}^0$
, and by diagonal intersection,
$\nu <\xi _{m+1}^0$
, and by diagonal intersection,
![]() $\xi _{m+1},...,\xi _{k_1}\in A_\nu $
. It follows that
$\xi _{m+1},...,\xi _{k_1}\in A_\nu $
. It follows that
Also,
![]() $p_{\nu }^{\smallfrown }{\langle }\xi _1,...,\xi _m{}{\rangle }^{\smallfrown }{\langle }\xi _{m+1},...,\xi _{m+k}{\rangle }\leq q$
hence in G. Hence
$p_{\nu }^{\smallfrown }{\langle }\xi _1,...,\xi _m{}{\rangle }^{\smallfrown }{\langle }\xi _{m+1},...,\xi _{m+k}{\rangle }\leq q$
hence in G. Hence
as wanted.
Now, as in the previous section, the following holds.
Theorem 4.5. Let
![]() $G\subseteq {\mathcal P}_E$
be a generic. Suppose that
$G\subseteq {\mathcal P}_E$
be a generic. Suppose that
![]() $A\in V[G]\setminus V$
is a subset of
$A\in V[G]\setminus V$
is a subset of
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $\kappa $
changes its cofinality to
$\kappa $
changes its cofinality to
![]() $\omega $
in
$\omega $
in
![]() $V[A]$
.
$V[A]$
.
4.3 The Merimovich version
The previous subsection implies in particular that
![]() ${\mathcal P}_E$
and
${\mathcal P}_E$
and
![]() $\mathbb {P}_E$
with P-points cannot add
$\mathbb {P}_E$
with P-points cannot add
![]() $\kappa ^{++}$
-many mutually generic Cohen functions. In this subsection, we will provide the general argument that the Extender-based Prikry forcing
$\kappa ^{++}$
-many mutually generic Cohen functions. In this subsection, we will provide the general argument that the Extender-based Prikry forcing
![]() $\mathbb {P}_E$
cannot add
$\mathbb {P}_E$
cannot add
![]() $\kappa ^{++}$
-many distinct subsets of
$\kappa ^{++}$
-many distinct subsets of
![]() $\kappa $
which preserves even the regularity of
$\kappa $
which preserves even the regularity of
![]() $\kappa $
.
$\kappa $
.
Theorem 4.6. Assume GCHFootnote
9
and let E be an extender over
![]() $\kappa $
. Let G be a generic subset of
$\kappa $
. Let G be a generic subset of
![]() $\mathbb {P}_E$
and let
$\mathbb {P}_E$
and let
![]() ${\langle } {A}_\alpha \mid \alpha <\kappa ^{++} {\rangle }$
be different subsets of
${\langle } {A}_\alpha \mid \alpha <\kappa ^{++} {\rangle }$
be different subsets of
![]() $\kappa $
in
$\kappa $
in
![]() $V[G]$
. Then there is
$V[G]$
. Then there is
![]() $I\subseteq \kappa ^{++}, I\in V, |I|=\kappa $
such that
$I\subseteq \kappa ^{++}, I\in V, |I|=\kappa $
such that
![]() $\kappa $
is a singular cardinal of cofinality
$\kappa $
is a singular cardinal of cofinality
![]() $\omega $
in
$\omega $
in
![]() $V[{\langle } {A}_\alpha \mid \alpha \in I{\rangle }]$
. In particular, there is no intermediate model of
$V[{\langle } {A}_\alpha \mid \alpha \in I{\rangle }]$
. In particular, there is no intermediate model of
![]() $V[G]$
where
$V[G]$
where
![]() $\kappa $
is measurable and
$\kappa $
is measurable and
![]() $2^{\kappa }>\kappa ^+$
.
$2^{\kappa }>\kappa ^+$
.
Proof Let
![]() be
be
![]() $\mathbb {P}_E$
-names of subsets of
$\mathbb {P}_E$
-names of subsets of
![]() $\kappa $
. We will confuse them sometimes with their characteristic functions. Work in V, and for every
$\kappa $
. We will confuse them sometimes with their characteristic functions. Work in V, and for every
![]() $\alpha <\kappa ^{++}$
, let
$\alpha <\kappa ^{++}$
, let
![]() $N_\alpha $
be an elementary submodel of
$N_\alpha $
be an elementary submodel of
![]() $H_\theta $
of cardinality
$H_\theta $
of cardinality
![]() $\kappa $
such that
$\kappa $
such that
![]() ${}^{\kappa>}N_\alpha \subseteq N_\alpha $
,
${}^{\kappa>}N_\alpha \subseteq N_\alpha $
,
![]() .
.
Let
![]() $f_\alpha \in \mathbb {P}^*_E$
be
$f_\alpha \in \mathbb {P}^*_E$
be
![]() $N_\alpha $
-completely generic, i.e.,
$N_\alpha $
-completely generic, i.e.,
![]() $f_\alpha ^\frown {\langle } \vec {\nu }_1,...,\vec {\nu }_n{\rangle }\in \mathbb {P}^*_E$
is
$f_\alpha ^\frown {\langle } \vec {\nu }_1,...,\vec {\nu }_n{\rangle }\in \mathbb {P}^*_E$
is
![]() $N_\alpha $
-generic.
$N_\alpha $
-generic.
Using
![]() $\Delta $
-system-like arguments, we can assume that
$\Delta $
-system-like arguments, we can assume that
![]() ${\langle } f_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
form a
${\langle } f_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
form a
![]() $\Delta $
-system such that for every
$\Delta $
-system such that for every
![]() $\alpha , \beta <\kappa ^{++}$
,
$\alpha , \beta <\kappa ^{++}$
,
-
(1)
 $otp(\operatorname {\mathrm {dom}}(f_\alpha ))=otp(\operatorname {\mathrm {dom}}(f_\beta ))$
, and the order isomorphism between
$otp(\operatorname {\mathrm {dom}}(f_\alpha ))=otp(\operatorname {\mathrm {dom}}(f_\beta ))$
, and the order isomorphism between
 $\operatorname {\mathrm {dom}}(f_\alpha )$
and
$\operatorname {\mathrm {dom}}(f_\alpha )$
and
 $\operatorname {\mathrm {dom}}(f_\beta )$
,
$\operatorname {\mathrm {dom}}(f_\beta )$
,
 $\sigma _{\alpha ,\beta }$
is constant on the intersection
$\sigma _{\alpha ,\beta }$
is constant on the intersection
 $\operatorname {\mathrm {dom}}(f_{\alpha })\cap \operatorname {\mathrm {dom}}(f_{\beta })$
.
$\operatorname {\mathrm {dom}}(f_{\alpha })\cap \operatorname {\mathrm {dom}}(f_{\beta })$
. -
(2) for every
 $\rho \in \operatorname {\mathrm {dom}}(f_\alpha )$
,
$\rho \in \operatorname {\mathrm {dom}}(f_\alpha )$
,
 $f_\alpha (\rho )=f_\beta (\sigma _{\alpha \beta }(\rho ))$
.
$f_\alpha (\rho )=f_\beta (\sigma _{\alpha \beta }(\rho ))$
.
Attach to each
![]() $\alpha <\kappa ^+$
an
$\alpha <\kappa ^+$
an
![]() $E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-large tree
$E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-large tree
![]() $T_\alpha $
. Define
$T_\alpha $
. Define
![]() $T_\alpha $
level by level as follows. Set
$T_\alpha $
level by level as follows. Set
![]() $Lev_1(T_\alpha )=S_\alpha ^0\cup S_\alpha ^1$
, where:
$Lev_1(T_\alpha )=S_\alpha ^0\cup S_\alpha ^1$
, where:
-
(1) for every
 $\vec {\nu }\in S_\alpha ^0$
,
$\vec {\nu }\in S_\alpha ^0$
,
 $\operatorname {\mathrm {dom}}(\vec {\nu })$
contains elements in
$\operatorname {\mathrm {dom}}(\vec {\nu })$
contains elements in
 $\operatorname {\mathrm {dom}}(f_\alpha )\setminus \operatorname {\mathrm {dom}}(f_0)$
, if
$\operatorname {\mathrm {dom}}(f_\alpha )\setminus \operatorname {\mathrm {dom}}(f_0)$
, if
 $\alpha>0$
,
$\alpha>0$
, -
(2) if
 $\alpha =0$
, then
$\alpha =0$
, then
 $S_\alpha ^0= S_\alpha ^1$
,
$S_\alpha ^0= S_\alpha ^1$
, -
(3)
 $S_\alpha ^1\hspace{-0.5pt}=\hspace{-0.5pt} \{\vec {\nu }\hspace{-0.5pt}\mid\hspace{-0.5pt} \vec {\nu } \text { is an increasing partial function from} \operatorname {\mathrm {dom}}(f_0)\hspace{-0.5pt}\cap\hspace{-0.5pt} \operatorname {\mathrm {dom}}(f_\alpha ) \text { to } \kappa \}$
, if
$S_\alpha ^1\hspace{-0.5pt}=\hspace{-0.5pt} \{\vec {\nu }\hspace{-0.5pt}\mid\hspace{-0.5pt} \vec {\nu } \text { is an increasing partial function from} \operatorname {\mathrm {dom}}(f_0)\hspace{-0.5pt}\cap\hspace{-0.5pt} \operatorname {\mathrm {dom}}(f_\alpha ) \text { to } \kappa \}$
, if
 $\alpha>0$
,
$\alpha>0$
, -
(4) for every
 $ \vec {\nu } \in S_\alpha ^0$
, the following holds:
$ \vec {\nu } \in S_\alpha ^0$
, the following holds: ${\langle } f_\alpha {}^\frown \vec {\nu },B_{\vec {\nu }}{\rangle }$
decides
${\langle } f_\alpha {}^\frown \vec {\nu },B_{\vec {\nu }}{\rangle }$
decides
 for some
for some
 $E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-tree
$E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-tree
 $B_{\vec {\nu }}$
and such that the decision depends only on
$B_{\vec {\nu }}$
and such that the decision depends only on
 $\vec {\nu }(\kappa )$
.
$\vec {\nu }(\kappa )$
.
In order to find such a tree, we will use the fact that
![]() $f_\alpha \in \mathbb {P}_E^*$
is
$f_\alpha \in \mathbb {P}_E^*$
is
![]() $N_\alpha $
-generic, and the set
$N_\alpha $
-generic, and the set
being dense open in
![]() $\mathbb {P}_E^*$
. This implies the existence of an
$\mathbb {P}_E^*$
. This implies the existence of an
![]() $E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-tree
$E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-tree
![]() $B_{\vec {\nu }}$
such that
$B_{\vec {\nu }}$
such that
Next, in order to make the decision to depend only on
![]() $\vec {\nu }(\kappa )$
, we use ineffability: Suppose that
$\vec {\nu }(\kappa )$
, we use ineffability: Suppose that
![]() ${\langle } f_\alpha {}^\frown \vec {\nu }, B_{\vec {\nu }}{\rangle }$
forces that
${\langle } f_\alpha {}^\frown \vec {\nu }, B_{\vec {\nu }}{\rangle }$
forces that
. Let g be the function
![]() $g(\vec {\nu })=A_\alpha (\vec {\nu })$
. It follows that
$g(\vec {\nu })=A_\alpha (\vec {\nu })$
. It follows that
Also, since
![]() $crit(j)=\kappa $
, it follows that
$crit(j)=\kappa $
, it follows that
![]() $j(X_\alpha ({\langle }{\rangle }))\cap \kappa =X_\alpha ({\langle }{\rangle })$
. Combine this together with the fact that
$j(X_\alpha ({\langle }{\rangle }))\cap \kappa =X_\alpha ({\langle }{\rangle })$
. Combine this together with the fact that
to find an
![]() $E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-large set
$E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-large set
![]() $S^0_\alpha $
, such that
$S^0_\alpha $
, such that
![]() $(1)$
holds and for all
$(1)$
holds and for all
![]() $\vec {\nu }\in S^0_\alpha $
,
$\vec {\nu }\in S^0_\alpha $
,
Finally, we let
![]() $Lev_1(T_{\alpha })=S^0_\alpha \cup S^1_\alpha $
. Note that if
$Lev_1(T_{\alpha })=S^0_\alpha \cup S^1_\alpha $
. Note that if
![]() $\alpha>0$
, then
$\alpha>0$
, then
![]() $S^0_\alpha $
and
$S^0_\alpha $
and
![]() $S^1_\alpha $
are disjoint and therefore
$S^1_\alpha $
are disjoint and therefore
![]() $S_\alpha ^1\not \in E(\operatorname {\mathrm {dom}}(f_\alpha ))$
. In general, we define by induction on n, then
$S_\alpha ^1\not \in E(\operatorname {\mathrm {dom}}(f_\alpha ))$
. In general, we define by induction on n, then
![]() $n^{\text {th}}$
level of
$n^{\text {th}}$
level of
![]() $T_\alpha $
. So let
$T_\alpha $
. So let
![]() ${\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle } \in Lev_n(T_\alpha )$
and let us define
${\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle } \in Lev_n(T_\alpha )$
and let us define
![]() $\operatorname {\mathrm {Succ}}_{T_\alpha }({\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle })=S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0\cup S_{\alpha , {\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^1$
, where:
$\operatorname {\mathrm {Succ}}_{T_\alpha }({\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle })=S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0\cup S_{\alpha , {\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^1$
, where:
-
(1) For every
 $\vec {\nu }\in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0\cup S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^1$
,
$\vec {\nu }\in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0\cup S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^1$
,
 $\vec {\nu }(\kappa )> \sup (\operatorname {\mathrm {rng}}({\rho }_n))$
.
$\vec {\nu }(\kappa )> \sup (\operatorname {\mathrm {rng}}({\rho }_n))$
. -
(2)
 $S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0\subseteq Suc_{B_{{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}}({\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle })$
.
$S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0\subseteq Suc_{B_{{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}}({\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle })$
. -
(3) If
 $\alpha>0$
, then for every
$\alpha>0$
, then for every
 $\vec {\nu }\in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0$
,
$\vec {\nu }\in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0$
,
 $\operatorname {\mathrm {dom}}(\vec {\nu })$
contains elements in
$\operatorname {\mathrm {dom}}(\vec {\nu })$
contains elements in
 $\operatorname {\mathrm {dom}}(f_\alpha )\setminus \operatorname {\mathrm {dom}}(f_0)$
.
$\operatorname {\mathrm {dom}}(f_\alpha )\setminus \operatorname {\mathrm {dom}}(f_0)$
. -
(4) If
 $\alpha =0$
, then
$\alpha =0$
, then
 $S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0= S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^1$
.
$S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0= S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^1$
. -
(5) If
 $\vec {\rho }_n\in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_{n-1}{\rangle }}^0$
and
$\vec {\rho }_n\in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_{n-1}{\rangle }}^0$
and
 $\alpha>0$
, then
$\alpha>0$
, then
 $S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^1=\emptyset $
.
$S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^1=\emptyset $
. -
(6) If
 $\vec {\rho }_n\in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_{n-1}{\rangle }}^1$
and
$\vec {\rho }_n\in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_{n-1}{\rangle }}^1$
and
 $\alpha>0$
, then
$\alpha>0$
, then  $$ \begin{align*}S_{\alpha,{\langle} \vec{\rho}_1,...,\vec{\rho}_n{\rangle}}^1 =\{\vec{\nu}\mid \vec{\nu} \text{ is an increasing partial function from }\end{align*} $$
$$ \begin{align*}S_{\alpha,{\langle} \vec{\rho}_1,...,\vec{\rho}_n{\rangle}}^1 =\{\vec{\nu}\mid \vec{\nu} \text{ is an increasing partial function from }\end{align*} $$
 $$ \begin{align*}\operatorname{\mathrm{dom}}(f_0)\cap \operatorname{\mathrm{dom}}(f_\alpha) \text{ to } \kappa, \vec{\nu}(\kappa)>\sup(\operatorname{\mathrm{rng}}(\vec{\rho}_n))\}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{dom}}(f_0)\cap \operatorname{\mathrm{dom}}(f_\alpha) \text{ to } \kappa, \vec{\nu}(\kappa)>\sup(\operatorname{\mathrm{rng}}(\vec{\rho}_n))\}.\end{align*} $$
-
(7) For every
 $ \vec {\nu } \in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0$
, the following holds:
$ \vec {\nu } \in S_{\alpha ,{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}^0$
, the following holds: ${\langle } f_\alpha {}^\frown {\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }^\frown {\langle } \vec {\nu }{\rangle }, B_{{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle },\vec {\nu }}{\rangle }$
decides
${\langle } f_\alpha {}^\frown {\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }^\frown {\langle } \vec {\nu }{\rangle }, B_{{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle },\vec {\nu }}{\rangle }$
decides
 and the decision depends only on
and the decision depends only on
 ${\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }{}^\frown \vec {\nu }(\kappa )$
,
${\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }{}^\frown \vec {\nu }(\kappa )$
,for some
 $E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-tree
$E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-tree
 $ B_{{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }, \vec {\nu }}$
, which is a subtree of
$ B_{{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }, \vec {\nu }}$
, which is a subtree of
 $B_{{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}$
.
$B_{{\langle } \vec {\rho }_1,...,\vec {\rho }_n{\rangle }}$
.
Denote by
![]() $T_\alpha ^0$
the tree
$T_\alpha ^0$
the tree
![]() $T_\alpha $
with
$T_\alpha $
with
![]() $S^1_{\alpha \vec {\nu }_1,...,\vec {\nu }_n}$
removed from
$S^1_{\alpha \vec {\nu }_1,...,\vec {\nu }_n}$
removed from
![]() $\operatorname {\mathrm {Succ}}_{T_\alpha }({\langle }\vec {\nu }_1,...,\vec {\nu }_n{\rangle })$
Footnote
10
. Clearly,
$\operatorname {\mathrm {Succ}}_{T_\alpha }({\langle }\vec {\nu }_1,...,\vec {\nu }_n{\rangle })$
Footnote
10
. Clearly,
![]() $T_\alpha ^0$
is still
$T_\alpha ^0$
is still
![]() $E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-tree.
$E(\operatorname {\mathrm {dom}}(f_\alpha ))$
-tree.
The tree
![]() $T^0_{\alpha }$
has the property that for every
$T^0_{\alpha }$
has the property that for every
![]() ${\langle }\vec {\nu }_1,...,\vec {\nu }_n{\rangle }\in T_{\alpha }$
(!), and every
${\langle }\vec {\nu }_1,...,\vec {\nu }_n{\rangle }\in T_{\alpha }$
(!), and every
![]() $\vec {\nu }\in \operatorname {\mathrm {Succ}}_{T^0_\alpha }({\langle }\vec {\nu }_1,...,\vec {\nu }_n{\rangle })$
, item
$\vec {\nu }\in \operatorname {\mathrm {Succ}}_{T^0_\alpha }({\langle }\vec {\nu }_1,...,\vec {\nu }_n{\rangle })$
, item
![]() $(2)$
above ensures that
$(2)$
above ensures that
![]() $(T^0_\alpha )_{{\langle }\vec {\nu }_1,...,\vec {\nu }_n,\vec {\nu }{\rangle }}\subseteq B_{{\langle }\vec {\nu }_1,...,\vec {\nu }_n,\vec {\nu }{\rangle }}$
and by item
$(T^0_\alpha )_{{\langle }\vec {\nu }_1,...,\vec {\nu }_n,\vec {\nu }{\rangle }}\subseteq B_{{\langle }\vec {\nu }_1,...,\vec {\nu }_n,\vec {\nu }{\rangle }}$
and by item
![]() $(7)$
we obtain
$(7)$
we obtain
By shrinking if necessary, we can assume that the trees are isomorphic under the obvious isomorphism induced by the
![]() $\Delta $
-system. Moreover, by
$\Delta $
-system. Moreover, by
![]() $GCH$
, there are only
$GCH$
, there are only
![]() $\kappa ^+$
-many possible decisions on a fixed isomorphism-type of trees, and therefore we can stabilize the decisions, so they do not depend on a particular choice of
$\kappa ^+$
-many possible decisions on a fixed isomorphism-type of trees, and therefore we can stabilize the decisions, so they do not depend on a particular choice of
![]() $\alpha $
. Let us now take
$\alpha $
. Let us now take
![]() $\kappa $
elements and combine them into a single condition. Namely, we consider
$\kappa $
elements and combine them into a single condition. Namely, we consider
![]() ${\langle }{\langle } f_\alpha , T_\alpha {\rangle } \mid 0<\alpha <\kappa {\rangle }$
and define a condition
${\langle }{\langle } f_\alpha , T_\alpha {\rangle } \mid 0<\alpha <\kappa {\rangle }$
and define a condition
![]() ${\langle } f^*,T^*{\rangle }$
as follows:
${\langle } f^*,T^*{\rangle }$
as follows:
Let
![]() $f^*=\bigcup _{0<\alpha <\kappa }f_\alpha $
. Define an
$f^*=\bigcup _{0<\alpha <\kappa }f_\alpha $
. Define an
![]() $E(\operatorname {\mathrm {dom}}(f^*))$
-tree
$E(\operatorname {\mathrm {dom}}(f^*))$
-tree
![]() $ T^*$
. It will be a sort of a diagonal intersection of
$ T^*$
. It will be a sort of a diagonal intersection of
![]() $T_\alpha , 0<\alpha <\kappa $
. Set
$T_\alpha , 0<\alpha <\kappa $
. Set
To see that
![]() $X\in E(\operatorname {\mathrm {dom}}(f^*))$
, note that
$X\in E(\operatorname {\mathrm {dom}}(f^*))$
, note that
Also, for every
![]() $\xi <\kappa $
,
$\xi <\kappa $
,
![]() $|j"\operatorname {\mathrm {dom}}(f^*)\cap \operatorname {\mathrm {dom}}(j(f_\xi ))|=|j"\operatorname {\mathrm {dom}}(f_\xi )|=|\operatorname {\mathrm {dom}}(f_\xi )|$
and since
$|j"\operatorname {\mathrm {dom}}(f^*)\cap \operatorname {\mathrm {dom}}(j(f_\xi ))|=|j"\operatorname {\mathrm {dom}}(f_\xi )|=|\operatorname {\mathrm {dom}}(f_\xi )|$
and since
![]() $f_\xi $
is completely generic we conclude that this cardinality must be
$f_\xi $
is completely generic we conclude that this cardinality must be
![]() $\kappa $
. Hence
$\kappa $
. Hence
![]() $(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}\in j(X)$
. Define the first level of the treeFootnote
11
$(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}\in j(X)$
. Define the first level of the treeFootnote
11
Then
![]() $Lev_1(T^*)\in E(\operatorname {\mathrm {dom}}(f^*))$
. To see this, it suffices to prove that the
$Lev_1(T^*)\in E(\operatorname {\mathrm {dom}}(f^*))$
. To see this, it suffices to prove that the
![]() $E(\operatorname {\mathrm {dom}}(f^*))$
is closed under the diagonal intersection
$E(\operatorname {\mathrm {dom}}(f^*))$
is closed under the diagonal intersection
![]() $\Delta ^*$
, so if
$\Delta ^*$
, so if
![]() ${\langle } X_\alpha \mid \alpha <\kappa {\rangle }\subseteq E(\operatorname {\mathrm {dom}}(f^*))$
, we claim that
${\langle } X_\alpha \mid \alpha <\kappa {\rangle }\subseteq E(\operatorname {\mathrm {dom}}(f^*))$
, we claim that
![]() $(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}\in j(\Delta ^*_{\alpha <\kappa }X_\alpha )$
. Indeed, for every
$(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}\in j(\Delta ^*_{\alpha <\kappa }X_\alpha )$
. Indeed, for every
![]() $\alpha <\kappa =(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}(j(\kappa ))$
,
$\alpha <\kappa =(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}(j(\kappa ))$
,
![]() $j(\alpha )=\alpha $
and the
$j(\alpha )=\alpha $
and the
![]() $\alpha ^{\text {th}}$
element in the sequence
$\alpha ^{\text {th}}$
element in the sequence
![]() $j({\langle } X_\alpha \mid \alpha <\kappa {\rangle })$
is
$j({\langle } X_\alpha \mid \alpha <\kappa {\rangle })$
is
![]() $j(X_\alpha )$
. Since
$j(X_\alpha )$
. Since
![]() $X_\alpha $
is assumed to be in
$X_\alpha $
is assumed to be in
![]() $E(\operatorname {\mathrm {dom}}(f^*))$
we conclude that
$E(\operatorname {\mathrm {dom}}(f^*))$
we conclude that
![]() $(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}\in j(X_\alpha )$
. By the definition of
$(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}\in j(X_\alpha )$
. By the definition of
![]() $\Delta ^*$
, and elementarity of j, we conclude that
$\Delta ^*$
, and elementarity of j, we conclude that
![]() $(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}\in j(\Delta ^*_{\alpha <\kappa }X_\alpha )$
.
$(j\restriction \operatorname {\mathrm {dom}}(f^*))^{-1}\in j(\Delta ^*_{\alpha <\kappa }X_\alpha )$
.
We continue to define inductively the level of
![]() $T^*$
. Let now
$T^*$
. Let now
![]() ${\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle } \in Lev_n(T^*)$
, and define
${\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle } \in Lev_n(T^*)$
, and define
![]() $\operatorname {\mathrm {Succ}}_{T^*}({\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle })$
. As above, we consider first the set
$\operatorname {\mathrm {Succ}}_{T^*}({\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle })$
. As above, we consider first the set
Clearly,
![]() $X_{{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle }}\in E(\operatorname {\mathrm {dom}}(f^*))$
. Let
$X_{{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle }}\in E(\operatorname {\mathrm {dom}}(f^*))$
. Let
![]() $\operatorname {\mathrm {Succ}}_{T^*}({\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle })$
be the set
$\operatorname {\mathrm {Succ}}_{T^*}({\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle })$
be the set
Once we ensure that for every
![]() $\xi <\kappa $
,
$\xi <\kappa $
,
![]() $\operatorname {\mathrm {Succ}}_{T_\xi ^0}({\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle })$
is well defined, then
$\operatorname {\mathrm {Succ}}_{T_\xi ^0}({\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle })$
is well defined, then
![]() $T^*$
will form an
$T^*$
will form an
![]() $E(\operatorname {\mathrm {dom}}(f^*))$
-fat tree. Namely, we need to prove that:
$E(\operatorname {\mathrm {dom}}(f^*))$
-fat tree. Namely, we need to prove that:
Claim 4.7. For every
![]() $\xi <\kappa $
,
$\xi <\kappa $
,
![]() ${\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle }\in Lev_n(T_\xi )$
. Moreover,
${\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle }\in Lev_n(T_\xi )$
. Moreover,
![]() $\xi <\vec {\rho }_1(\kappa )$
iff
$\xi <\vec {\rho }_1(\kappa )$
iff
![]() ${\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle }\in Lev_n(T^0_\xi )$
.
${\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle }\in Lev_n(T^0_\xi )$
.
Proof of Claim 4.7
For every
![]() $\xi <\vec {\rho }_1(\kappa )$
, we have
$\xi <\vec {\rho }_1(\kappa )$
, we have
and therefore
![]() $\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi )\in Lev_1(T^0_\xi )$
. If
$\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi )\in Lev_1(T^0_\xi )$
. If
![]() $\xi \geq \vec {\rho }_1(\kappa )$
, then since
$\xi \geq \vec {\rho }_1(\kappa )$
, then since
![]() $\vec {\rho }_1\in X$
, the
$\vec {\rho }_1\in X$
, the
![]() $\Delta $
-system ensures that
$\Delta $
-system ensures that
![]() $\operatorname {\mathrm {dom}}(\vec {\rho }_1)\cap \operatorname {\mathrm {dom}}(f_\xi )=\operatorname {\mathrm {dom}}(\vec {\rho }_1)\cap \operatorname {\mathrm {dom}}(f_0)\subseteq \operatorname {\mathrm {dom}}(f_0)\cap \operatorname {\mathrm {dom}}(f_\xi )$
. It follows from the definition that
$\operatorname {\mathrm {dom}}(\vec {\rho }_1)\cap \operatorname {\mathrm {dom}}(f_\xi )=\operatorname {\mathrm {dom}}(\vec {\rho }_1)\cap \operatorname {\mathrm {dom}}(f_0)\subseteq \operatorname {\mathrm {dom}}(f_0)\cap \operatorname {\mathrm {dom}}(f_\xi )$
. It follows from the definition that
![]() $\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi )=\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_0)\in S^1_\alpha \subseteq Lev_1(T_\alpha )$
. Suppose that
$\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi )=\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_0)\in S^1_\alpha \subseteq Lev_1(T_\alpha )$
. Suppose that
![]() ${\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle }\in Lev_n(T_\xi )$
, and let
${\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle }\in Lev_n(T_\xi )$
, and let
![]() $\vec {\rho }_{n+1}\in Succ_{T^*}({\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle })$
. Then for every
$\vec {\rho }_{n+1}\in Succ_{T^*}({\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle })$
. Then for every
![]() $\xi <\vec {\rho }_{n+1}(\kappa )$
,
$\xi <\vec {\rho }_{n+1}(\kappa )$
,
![]() $\vec {\rho }_{n+1}\restriction \operatorname {\mathrm {dom}}(f_\xi )\in \operatorname {\mathrm {Succ}}_{T^0_\xi }({\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle })$
by the definition of the diagonal intersection. If
$\vec {\rho }_{n+1}\restriction \operatorname {\mathrm {dom}}(f_\xi )\in \operatorname {\mathrm {Succ}}_{T^0_\xi }({\langle }\vec {\rho }_1\restriction \operatorname {\mathrm {dom}}(f_\xi ),...,\vec {\rho }_n\restriction \operatorname {\mathrm {dom}}(f_\xi ){\rangle })$
by the definition of the diagonal intersection. If
![]() $\xi \geq \vec {\rho }_{n+1}(\kappa )$
, then, as before,
$\xi \geq \vec {\rho }_{n+1}(\kappa )$
, then, as before,
![]() $\vec {\rho }_{n+1}\restriction \operatorname {\mathrm {dom}}(f_\xi )\in S^1_{\xi ,{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle }}$
.
$\vec {\rho }_{n+1}\restriction \operatorname {\mathrm {dom}}(f_\xi )\in S^1_{\xi ,{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle }}$
.
![]() $Lev_1(T^*)$
has the property that for all
$Lev_1(T^*)$
has the property that for all
![]() $\vec {\rho }\in Lev_1(T^*)$
and
$\vec {\rho }\in Lev_1(T^*)$
and
![]() $\alpha <\vec {\rho }(\kappa )$
,
$\alpha <\vec {\rho }(\kappa )$
,
Hence, by
![]() $(*)$
,
$(*)$
,
![]() ${\langle } f^*{}^\frown \vec {\rho }, (T^*)_{\vec {\rho }}{\rangle }$
also forces
${\langle } f^*{}^\frown \vec {\rho }, (T^*)_{\vec {\rho }}{\rangle }$
also forces
![]() . In addition, if we have
. In addition, if we have
![]() $\alpha ,\beta < \vec {\rho }(\kappa )$
, then
$\alpha ,\beta < \vec {\rho }(\kappa )$
, then
![]() ,
,
![]() depends only on
depends only on
![]() $(\vec {\rho }\restriction \operatorname {\mathrm {dom}}(f_\alpha ))(\kappa )=\vec {\rho }(\kappa )=(\vec {\rho }\restriction \operatorname {\mathrm {dom}}(f_\beta ))(\kappa )$
, and since the isomorphism
$(\vec {\rho }\restriction \operatorname {\mathrm {dom}}(f_\alpha ))(\kappa )=\vec {\rho }(\kappa )=(\vec {\rho }\restriction \operatorname {\mathrm {dom}}(f_\beta ))(\kappa )$
, and since the isomorphism
![]() $\sigma _{\alpha ,\beta }$
fixes
$\sigma _{\alpha ,\beta }$
fixes
![]() $\kappa $
(as
$\kappa $
(as
![]() $\kappa \in \operatorname {\mathrm {dom}}(f_\alpha )\cap \operatorname {\mathrm {dom}}(f_\beta )$
) it follows that
$\kappa \in \operatorname {\mathrm {dom}}(f_\alpha )\cap \operatorname {\mathrm {dom}}(f_\beta )$
) it follows that
![]() are decided to be the same set.
are decided to be the same set.
Next consider
![]() ${\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle }\in T^*$
, by Claim 4.7, and we have that for all
${\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle }\in T^*$
, by Claim 4.7, and we have that for all
![]() $\alpha <\vec {\rho }_n(\kappa )$
,
$\alpha <\vec {\rho }_n(\kappa )$
,
However, since the decision about
![]() depends now on
depends now on
![]() ${\langle }\vec {\rho }_1,...,\vec {\rho }_{n-1}{\rangle }^{\smallfrown }\vec {\rho }_n(\kappa )$
, then if
${\langle }\vec {\rho }_1,...,\vec {\rho }_{n-1}{\rangle }^{\smallfrown }\vec {\rho }_n(\kappa )$
, then if
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
are below
$\beta $
are below
![]() $\vec {\rho }_{n-1}(\kappa )$
, then
$\vec {\rho }_{n-1}(\kappa )$
, then
![]() $\vec {\rho }_{n-1}\restriction \operatorname {\mathrm {dom}}(f_\alpha )$
(or
$\vec {\rho }_{n-1}\restriction \operatorname {\mathrm {dom}}(f_\alpha )$
(or
![]() $\vec {\rho }_i\restriction \operatorname {\mathrm {dom}}(f_\alpha )$
for
$\vec {\rho }_i\restriction \operatorname {\mathrm {dom}}(f_\alpha )$
for
![]() $i<n$
) might include in its domain ordinals which are moved under the isomorphism
$i<n$
) might include in its domain ordinals which are moved under the isomorphism
![]() $\sigma _{\alpha ,\beta }$
and therefore we are not guaranteed that the decision about
$\sigma _{\alpha ,\beta }$
and therefore we are not guaranteed that the decision about
![]() is the same (up to
is the same (up to
![]() $\vec {\rho }_{1}(\kappa )$
it is still the same decision). However, if both
$\vec {\rho }_{1}(\kappa )$
it is still the same decision). However, if both
![]() $\alpha ,\beta \in [\vec {\rho }_{n-1}(\kappa ),\vec {\rho }_n(\kappa ))$
, we have the following claim:
$\alpha ,\beta \in [\vec {\rho }_{n-1}(\kappa ),\vec {\rho }_n(\kappa ))$
, we have the following claim:
Claim 4.8. If
![]() $\alpha ,\beta \in [\vec {\rho }_{n-1}(\kappa ),\vec {\rho }_n(\kappa ))$
then
$\alpha ,\beta \in [\vec {\rho }_{n-1}(\kappa ),\vec {\rho }_n(\kappa ))$
then
![]() ${\langle } f^*{}^{\smallfrown }{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle },(T^*)_{{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle }}{\rangle }$
decides the values of
${\langle } f^*{}^{\smallfrown }{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle },(T^*)_{{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle }}{\rangle }$
decides the values of
![]() and
and
![]() to be the same.
to be the same.
Proof of Claim 4.8
By definition, for every
![]() $1\leq i<n$
,
$1\leq i<n$
,
![]() $\vec {\rho }_{i}\in X_{{\langle }\vec {\rho }_{1},...,\vec {\rho }_{i-1}{\rangle }}$
. Since
$\vec {\rho }_{i}\in X_{{\langle }\vec {\rho }_{1},...,\vec {\rho }_{i-1}{\rangle }}$
. Since
![]() $\alpha ,\beta \geq \vec {\rho }_{n-1}(\kappa )\geq \vec {\rho }_i(\kappa )$
,
$\alpha ,\beta \geq \vec {\rho }_{n-1}(\kappa )\geq \vec {\rho }_i(\kappa )$
,
Since the isomorphism
![]() $\sigma _{\alpha ,\beta }$
fixes the kernel of the
$\sigma _{\alpha ,\beta }$
fixes the kernel of the
![]() $\Delta $
-system, we have that the decision of
$\Delta $
-system, we have that the decision of
about
![]() and the decision of
and the decision of
about
![]() is the same. By
is the same. By
![]() $(**)$
, the condition
$(**)$
, the condition
![]() ${\langle } f^*{}^{\smallfrown }{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle },(T^*)_{\vec {\rho }_1,...,\vec {\rho }_n}{\rangle }$
decides the values the same way.
${\langle } f^*{}^{\smallfrown }{\langle }\vec {\rho }_1,...,\vec {\rho }_n{\rangle },(T^*)_{\vec {\rho }_1,...,\vec {\rho }_n}{\rangle }$
decides the values the same way.
Using density arguments we can assume that such defined condition
![]() ${\langle } f^*,T^*{\rangle }$
is in the generic subset G of
${\langle } f^*,T^*{\rangle }$
is in the generic subset G of
![]() $\mathbb {P}_E$
. Denote by
$\mathbb {P}_E$
. Denote by
![]() ${\langle } \kappa _n \mid n<\omega {\rangle }$
the Prikry sequence for the normal measure
${\langle } \kappa _n \mid n<\omega {\rangle }$
the Prikry sequence for the normal measure
![]() $E_\kappa $
.
$E_\kappa $
.
It follows that the sets
![]() ${\langle } A_\alpha \mid \alpha <\kappa {\rangle }$
have the following property in
${\langle } A_\alpha \mid \alpha <\kappa {\rangle }$
have the following property in
![]() $V[G]$
:
$V[G]$
:
Now, let us turn to the model
![]() $M^*=V[{\langle } A_\alpha \mid \alpha <\kappa {\rangle }]$
and prove that
$M^*=V[{\langle } A_\alpha \mid \alpha <\kappa {\rangle }]$
and prove that
![]() $cf^{M^*}(\kappa )=\omega $
. Let us define in
$cf^{M^*}(\kappa )=\omega $
. Let us define in
![]() $M^*$
an
$M^*$
an
![]() $\omega $
-sequence
$\omega $
-sequence
![]() ${\langle }\zeta _n\mid n<\omega {\rangle }$
as follows:
${\langle }\zeta _n\mid n<\omega {\rangle }$
as follows:
First, let
![]() $\zeta ^{\prime }_0$
be the least such that for some for some
$\zeta ^{\prime }_0$
be the least such that for some for some
![]() $\alpha ,\beta <\kappa $
,
$\alpha ,\beta <\kappa $
,
![]() $A_\alpha \cap \zeta _0^{\prime }\neq A_\beta \cap \zeta _0^{\prime }$
. There exists such
$A_\alpha \cap \zeta _0^{\prime }\neq A_\beta \cap \zeta _0^{\prime }$
. There exists such
![]() $\zeta _0^{\prime }$
since the sets in the sequence
$\zeta _0^{\prime }$
since the sets in the sequence
![]() ${\langle } A_\alpha \mid \alpha <\kappa {\rangle }$
are distinct. Let
${\langle } A_\alpha \mid \alpha <\kappa {\rangle }$
are distinct. Let
![]() $\zeta ^{\prime \prime }_0$
be the least such that for some
$\zeta ^{\prime \prime }_0$
be the least such that for some
![]() $\alpha <\zeta ^{\prime \prime }_0$
,
$\alpha <\zeta ^{\prime \prime }_0$
,
![]() $A_\alpha \cap \zeta _0^{\prime }\neq A_{\zeta _0^{\prime \prime }}\cap \zeta _0^{\prime }$
. Define
$A_\alpha \cap \zeta _0^{\prime }\neq A_{\zeta _0^{\prime \prime }}\cap \zeta _0^{\prime }$
. Define
![]() $\zeta _0=\max (\zeta _0^{\prime },\zeta _0^{\prime \prime })$
$\zeta _0=\max (\zeta _0^{\prime },\zeta _0^{\prime \prime })$
Claim 4.9.
![]() $\zeta _0\geq \kappa _0$
.
$\zeta _0\geq \kappa _0$
.
Proof of Claim 4.9
If
![]() $\zeta _0^{\prime }\geq \kappa _0$
then we are done. Otherwise, suppose
$\zeta _0^{\prime }\geq \kappa _0$
then we are done. Otherwise, suppose
![]() $\zeta _0^{\prime }\leq \kappa _0$
, then by
$\zeta _0^{\prime }\leq \kappa _0$
, then by
![]() $(***)$
for every
$(***)$
for every
![]() $\alpha <\beta <\kappa _0$
, we have
$\alpha <\beta <\kappa _0$
, we have
![]() $A_\alpha \cap \zeta _0^{\prime }=A_\beta \cap \zeta ^{\prime }_0$
. Hence by the definition of
$A_\alpha \cap \zeta _0^{\prime }=A_\beta \cap \zeta ^{\prime }_0$
. Hence by the definition of
![]() $\zeta ^{\prime \prime }_0$
, we have
$\zeta ^{\prime \prime }_0$
, we have
![]() $\zeta ^{\prime \prime }_0\geq \kappa _0$
and also
$\zeta ^{\prime \prime }_0\geq \kappa _0$
and also
![]() $\zeta _0\geq \kappa _0$
.
$\zeta _0\geq \kappa _0$
.
Suppose that
![]() $\zeta _n<\kappa $
was defined. Then the sequence
$\zeta _n<\kappa $
was defined. Then the sequence
![]() ${\langle } A_\alpha \mid \zeta _n<\alpha <\kappa {\rangle }$
consists of
${\langle } A_\alpha \mid \zeta _n<\alpha <\kappa {\rangle }$
consists of
![]() $\kappa $
-many distinct subsets of
$\kappa $
-many distinct subsets of
![]() $\kappa $
. Since
$\kappa $
. Since
![]() $\kappa $
is strong limit in
$\kappa $
is strong limit in
![]() $V[G]$
,
$V[G]$
,
![]() $2^{\zeta _n}<\kappa $
, hence there must be
$2^{\zeta _n}<\kappa $
, hence there must be
![]() $\zeta _n<\alpha <\beta <\kappa $
such that
$\zeta _n<\alpha <\beta <\kappa $
such that
![]() $A_\alpha \setminus \zeta _n+1\neq A_\beta \setminus \zeta _n+1$
. Let
$A_\alpha \setminus \zeta _n+1\neq A_\beta \setminus \zeta _n+1$
. Let
![]() $\zeta ^{\prime }_{n+1}$
be the minimal such that for some
$\zeta ^{\prime }_{n+1}$
be the minimal such that for some
![]() $\zeta _n<\alpha <\beta <\kappa $
,
$\zeta _n<\alpha <\beta <\kappa $
,
![]() $A_\alpha \cap \zeta ^{\prime }_{n+1}=A_{\beta }\cap \zeta ^{\prime }_{n+1}$
. Finally, let
$A_\alpha \cap \zeta ^{\prime }_{n+1}=A_{\beta }\cap \zeta ^{\prime }_{n+1}$
. Finally, let
![]() $\zeta _n<\zeta ^{\prime \prime }_{n+1}$
be the minimal such that for some
$\zeta _n<\zeta ^{\prime \prime }_{n+1}$
be the minimal such that for some
![]() $\alpha <\zeta ^{\prime \prime }_{n+1}$
,
$\alpha <\zeta ^{\prime \prime }_{n+1}$
,
![]() $A_\alpha \cap \zeta ^{\prime }_{n+1}\neq A_{\zeta ^{\prime \prime }_{n+1}}\cap \zeta ^{\prime }_{n+1}$
and
$A_\alpha \cap \zeta ^{\prime }_{n+1}\neq A_{\zeta ^{\prime \prime }_{n+1}}\cap \zeta ^{\prime }_{n+1}$
and
![]() $\zeta _{n+1}=\max (\zeta ^{\prime }_{n+1},\zeta ^{\prime \prime }_{n+1})$
. To conclude that
$\zeta _{n+1}=\max (\zeta ^{\prime }_{n+1},\zeta ^{\prime \prime }_{n+1})$
. To conclude that
![]() $cf^{M^*}(\kappa )=\omega $
is suffices to prove the following lemma:
$cf^{M^*}(\kappa )=\omega $
is suffices to prove the following lemma:
Claim 4.10. For every
![]() $n<\omega $
,
$n<\omega $
,
![]() $\zeta _n\geq \kappa _n$
.
$\zeta _n\geq \kappa _n$
.
Proof of Claim 4.10
By induction, for
![]() $n=0$
this is just the previous claim. Suppose that
$n=0$
this is just the previous claim. Suppose that
![]() $\zeta _n\geq \kappa _n$
, and toward a contradiction suppose that
$\zeta _n\geq \kappa _n$
, and toward a contradiction suppose that
![]() $\zeta _{n+1}<\kappa _{n+1}$
. Then by definition, there is
$\zeta _{n+1}<\kappa _{n+1}$
. Then by definition, there is
![]() $\alpha $
, such that
$\alpha $
, such that
![]() $\kappa _n\leq \zeta _n<\alpha <\zeta ^{\prime \prime }_{n+1}<\kappa _{n+1}$
such that
$\kappa _n\leq \zeta _n<\alpha <\zeta ^{\prime \prime }_{n+1}<\kappa _{n+1}$
such that
![]() $A_\alpha \cap \zeta ^{\prime }_{n+1}\neq A_{\zeta ^{\prime \prime }_{n+1}}\cap \zeta ^{\prime }_{n+1}$
. However, since
$A_\alpha \cap \zeta ^{\prime }_{n+1}\neq A_{\zeta ^{\prime \prime }_{n+1}}\cap \zeta ^{\prime }_{n+1}$
. However, since
![]() $\zeta ^{\prime }_{n+1}<\kappa _{n+1}$
we reached a contradiction to
$\zeta ^{\prime }_{n+1}<\kappa _{n+1}$
we reached a contradiction to
![]() $(***)$
, since we found two indices
$(***)$
, since we found two indices
![]() $\alpha ,\beta \in [\kappa _n,\kappa _{n+1})$
such that
$\alpha ,\beta \in [\kappa _n,\kappa _{n+1})$
such that
![]() $A_\alpha \cap \kappa _{n+1}\neq A_\beta \cap \kappa _{n+1}$
.
$A_\alpha \cap \kappa _{n+1}\neq A_\beta \cap \kappa _{n+1}$
.
The sequence
![]() ${\langle } \zeta _n \mid n<\omega {\rangle }$
will be a cofinal sequence in
${\langle } \zeta _n \mid n<\omega {\rangle }$
will be a cofinal sequence in
![]() $\kappa $
which belongs to
$\kappa $
which belongs to
![]() $V[{\langle } A_\alpha \mid \alpha <\kappa {\rangle }]$
.
$V[{\langle } A_\alpha \mid \alpha <\kappa {\rangle }]$
.
It turns out that
![]() $\mathbb {P}_E$
can add
$\mathbb {P}_E$
can add
![]() $\kappa ^+$
-many mutually generic over V Cohen functions, for specially chosen extender E.
$\kappa ^+$
-many mutually generic over V Cohen functions, for specially chosen extender E.
Theorem 4.11. Assume
![]() $GCH$
and suppose that E is a
$GCH$
and suppose that E is a
![]() $(\kappa ,\kappa ^{++})$
-extender. Then after the preparation of Theorem 2.10, there exists an extender
$(\kappa ,\kappa ^{++})$
-extender. Then after the preparation of Theorem 2.10, there exists an extender
![]() $E'$
such that
$E'$
such that
![]() $\mathbb {P}_{E'}$
adds
$\mathbb {P}_{E'}$
adds
![]() $\kappa ^+$
mutually generic over V Cohen functions.
$\kappa ^+$
mutually generic over V Cohen functions.
Proof Let
![]() $j=j_E:V\rightarrow M$
be the natural ultrapower by the
$j=j_E:V\rightarrow M$
be the natural ultrapower by the
![]() $(\kappa ,\kappa ^{++})-$
extender E, then
$(\kappa ,\kappa ^{++})-$
extender E, then
![]() $j(\kappa )>\kappa ^{++}$
,
$j(\kappa )>\kappa ^{++}$
,
![]() $crit(j)=\kappa $
, and
$crit(j)=\kappa $
, and
![]() ${}^{\kappa } M\subseteq M$
. Recall that the preparation forcing in Theorem 2.10 is an Easton support iteration
${}^{\kappa } M\subseteq M$
. Recall that the preparation forcing in Theorem 2.10 is an Easton support iteration
such that
is trivial unless
![]() $\beta $
is inaccessible in which case if
$\beta $
is inaccessible in which case if
![]() $\beta <\kappa $
then
$\beta <\kappa $
then
is a
![]() ${\mathcal P}_\beta $
-name for
${\mathcal P}_\beta $
-name for
![]() $\operatorname {\mathrm {LOTT}}(\operatorname {\mathrm {Cohen}}(\beta ,\beta ^+),\operatorname {\mathrm {Cohen}}(\beta ,\beta ^+)^2)$
. At
$\operatorname {\mathrm {LOTT}}(\operatorname {\mathrm {Cohen}}(\beta ,\beta ^+),\operatorname {\mathrm {Cohen}}(\beta ,\beta ^+)^2)$
. At
![]() $\kappa $
,
$\kappa $
,
is a name for
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
. Let
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
. Let
![]() $G_\kappa *g_\kappa $
be V-generic for
$G_\kappa *g_\kappa $
be V-generic for
. In
![]() $V[G_{\kappa }*g_\kappa ]$
we can construct an M-generic filter for
$V[G_{\kappa }*g_\kappa ]$
we can construct an M-generic filter for
by taking
![]() $G_\kappa *g_\kappa $
to be the generic up to
$G_\kappa *g_\kappa $
to be the generic up to
![]() $\kappa $
, including
$\kappa $
, including
![]() $\kappa $
and choosing that the lottery sum forces
$\kappa $
and choosing that the lottery sum forces
![]() $\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
(this forcing is the same in
$\operatorname {\mathrm {Cohen}}(\kappa ,\kappa ^+)$
(this forcing is the same in
![]() $V[G_\kappa ]$
and
$V[G_\kappa ]$
and
![]() $M[G_\kappa ]$
since
$M[G_\kappa ]$
since
![]() $(\kappa ^+)^{M[G_\kappa ]}=\kappa ^+$
and
$(\kappa ^+)^{M[G_\kappa ]}=\kappa ^+$
and
![]() $M[G_\kappa ]$
is closed under
$M[G_\kappa ]$
is closed under
![]() $\kappa $
-sequences of
$\kappa $
-sequences of
![]() $V[G_\kappa ]$
). Above
$V[G_\kappa ]$
). Above
![]() $\kappa $
we have sufficient closure, from the point of view of
$\kappa $
we have sufficient closure, from the point of view of
![]() $V[G_\kappa *g_\kappa ]$
, and by
$V[G_\kappa *g_\kappa ]$
, and by
![]() $GCH$
there are not too many dense open subsets of the tail forcing
$GCH$
there are not too many dense open subsets of the tail forcing
![]() ${\mathcal P}_{(\kappa ,j(\kappa )]}$
to meet, hence the embedding j lifts to
${\mathcal P}_{(\kappa ,j(\kappa )]}$
to meet, hence the embedding j lifts to
Since the cardinals in all the models are preserved, it follows that [Reference Cummings, Foreman and Kanamori12, Proposition 8.4]
So in
![]() $V[G_\kappa *g_\kappa ]$
the extender E extends to an extender
$V[G_\kappa *g_\kappa ]$
the extender E extends to an extender
![]() $E'={\langle } E^{\prime }_a\mid a\in [\kappa ]^{<\omega }{\rangle }$
defined by
$E'={\langle } E^{\prime }_a\mid a\in [\kappa ]^{<\omega }{\rangle }$
defined by
![]() $E^{\prime }_a=\{X\subseteq \kappa ^{|a|}\mid a\in j^*(X)\}$
.
$E^{\prime }_a=\{X\subseteq \kappa ^{|a|}\mid a\in j^*(X)\}$
.
Let W be the non-Galvin,
![]() $\kappa $
-complete ultrafilter over
$\kappa $
-complete ultrafilter over
![]() $\kappa $
with preparation for adding
$\kappa $
with preparation for adding
![]() $\kappa ^+$
-many Cohens (See Theorem 2.11).
$\kappa ^+$
-many Cohens (See Theorem 2.11).
Combine
![]() $E',W$
together as follows. First take an ultrapower with
$E',W$
together as follows. First take an ultrapower with
![]() $E'$
. Let
$E'$
. Let
![]() $j_{E'}:V \to M_{E'}$
be the corresponding embedding. Denote
$j_{E'}:V \to M_{E'}$
be the corresponding embedding. Denote
![]() $j_{E'}(\kappa )$
by
$j_{E'}(\kappa )$
by
![]() $\kappa _1$
and let
$\kappa _1$
and let
![]() $W'=j_{E'}(W)$
. Then take an ultrapower of
$W'=j_{E'}(W)$
. Then take an ultrapower of
![]() $M_{E'}$
with
$M_{E'}$
with
![]() $W'$
. Let
$W'$
. Let
![]() $j_{W'}:M_{E'} \to M$
be the corresponding embedding.
$j_{W'}:M_{E'} \to M$
be the corresponding embedding.
Consider
![]() $j_*=j_{W'}\circ j_{E'}:V\to M$
. Let
$j_*=j_{W'}\circ j_{E'}:V\to M$
. Let
![]() $E^*$
be the derived
$E^*$
be the derived
![]() $(\kappa ,\lambda )$
-extender for some
$(\kappa ,\lambda )$
-extender for some
![]() $\kappa _1<\lambda \leq j_*(\kappa )$
.
$\kappa _1<\lambda \leq j_*(\kappa )$
.
Note that
![]() $E^*(\kappa _1)=W$
, since for any
$E^*(\kappa _1)=W$
, since for any
![]() $X\subseteq \kappa $
,
$X\subseteq \kappa $
,
The Prikry forcing with W adds
![]() $\kappa ^+$
-many Cohens over V. This forcing is a part of
$\kappa ^+$
-many Cohens over V. This forcing is a part of
![]() $\mathbb {P}_{E^*}$
, since W appears as one of the measures of
$\mathbb {P}_{E^*}$
, since W appears as one of the measures of
![]() $E^*$
, which implies the theorem.
$E^*$
, which implies the theorem.
4.4 Cohen subsets of
 $\kappa ^+$
$\kappa ^+$
Let us argue here that both versions add
![]() $\kappa ^{++}$
-many (or
$\kappa ^{++}$
-many (or
![]() $\lambda $
-many if the extender has
$\lambda $
-many if the extender has
![]() $\lambda $
generators for a regular
$\lambda $
generators for a regular
![]() $\lambda>\kappa $
) Cohen subsets of
$\lambda>\kappa $
) Cohen subsets of
![]() $\kappa ^+$
mutually generic over V.
$\kappa ^+$
mutually generic over V.
Start with
![]() ${\mathcal P}_E$
of [Reference Gitik and Magidor21].
${\mathcal P}_E$
of [Reference Gitik and Magidor21].
Theorem 4.12. Let
![]() $G\subseteq {\mathcal P}_E$
be a generic. Then in
$G\subseteq {\mathcal P}_E$
be a generic. Then in
![]() $V[G]$
there is a sequence
$V[G]$
there is a sequence
![]() ${\langle } Z_\xi \mid \xi <\kappa ^{++}{\rangle }$
of mutually generic over V Cohen subsets of
${\langle } Z_\xi \mid \xi <\kappa ^{++}{\rangle }$
of mutually generic over V Cohen subsets of
![]() $\kappa ^+$
.
$\kappa ^+$
.
Proof Let
![]() ${\langle } t_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
be the Prikry sequences added by G.
${\langle } t_\alpha \mid \alpha <\kappa ^{++}{\rangle }$
be the Prikry sequences added by G.
Split, in V,
![]() $\kappa ^{++} $
into disjoint intervals
$\kappa ^{++} $
into disjoint intervals
![]() ${\langle } I_\xi \mid \xi <\kappa ^{++}{\rangle }$
order type of each
${\langle } I_\xi \mid \xi <\kappa ^{++}{\rangle }$
order type of each
![]() $\kappa ^+$
. Denote by
$\kappa ^+$
. Denote by
![]() $\sigma _\xi $
the order isomorphism between
$\sigma _\xi $
the order isomorphism between
![]() $I_\xi $
and
$I_\xi $
and
![]() $\kappa ^+$
.
$\kappa ^+$
.
Now, in
![]() $V[G]$
, set
$V[G]$
, set
Let us argue that such a sequence is as desired.
Work in V. Let
![]() $p\in {\mathcal P}$
and let D be a dense open subset of
$p\in {\mathcal P}$
and let D be a dense open subset of
![]() $\operatorname {\mathrm {Cohen}}(\kappa ^+, \kappa ^{++})$
.
$\operatorname {\mathrm {Cohen}}(\kappa ^+, \kappa ^{++})$
.
Let us find
![]() $q\geq p$
such that
$q\geq p$
such that
Extend first p to some r such that for every
![]() $\gamma \in \operatorname {\mathrm {Supp}}(r), r^\gamma $
is not equal to the empty sequence. Now, using
$\gamma \in \operatorname {\mathrm {Supp}}(r), r^\gamma $
is not equal to the empty sequence. Now, using
![]() $I_\xi ,\sigma _\xi $
’s turn
$I_\xi ,\sigma _\xi $
’s turn
![]() ${\langle } r^\gamma (0) \mid \gamma \in \operatorname {\mathrm {Supp}}(r){\rangle }$
into a condition in
${\langle } r^\gamma (0) \mid \gamma \in \operatorname {\mathrm {Supp}}(r){\rangle }$
into a condition in
![]() $\operatorname {\mathrm {Cohen}}(\kappa ^+, \kappa ^{++})$
. Extend it to one in D and move back to
$\operatorname {\mathrm {Cohen}}(\kappa ^+, \kappa ^{++})$
. Extend it to one in D and move back to
![]() ${\mathcal P}$
using
${\mathcal P}$
using
![]() $I_\xi ,\sigma _\xi ^{-1}$
’s. Finally, turn the result into a condition q in
$I_\xi ,\sigma _\xi ^{-1}$
’s. Finally, turn the result into a condition q in
![]() ${\mathcal P}$
stronger than r. It will be as desired.
${\mathcal P}$
stronger than r. It will be as desired.
The situation in the case of the Merimovich version is very similar:
Theorem 4.13. Let
![]() $G\subseteq \mathbb {P}_E$
be a generic. Then in
$G\subseteq \mathbb {P}_E$
be a generic. Then in
![]() $V[G]$
there is a sequence
$V[G]$
there is a sequence
![]() ${\langle } Z_\xi \mid \xi <\kappa ^{++}{\rangle }$
of mutually generic over V Cohen subsets of
${\langle } Z_\xi \mid \xi <\kappa ^{++}{\rangle }$
of mutually generic over V Cohen subsets of
![]() $\kappa ^+$
.
$\kappa ^+$
.
Proof Proceed as in Theorem 4.12 and define
![]() ${\langle } Z_\xi \mid \xi <\kappa ^{++}{\rangle }$
.
${\langle } Z_\xi \mid \xi <\kappa ^{++}{\rangle }$
.
Work in V. Let
![]() $p\in {\mathcal P}$
and let D be a dense open subset of
$p\in {\mathcal P}$
and let D be a dense open subset of
![]() $\operatorname {\mathrm {Cohen}}(\kappa ^+, \kappa ^{++})$
.
$\operatorname {\mathrm {Cohen}}(\kappa ^+, \kappa ^{++})$
.
Let us find
![]() $q\geq p$
such that
$q\geq p$
such that
A slight difference here is that the support of
![]() $p={\langle } f, T{\rangle }$
, i.e.,
$p={\langle } f, T{\rangle }$
, i.e.,
![]() $\operatorname {\mathrm {dom}}(f)$
may have
$\operatorname {\mathrm {dom}}(f)$
may have
![]() $\kappa $
many places
$\kappa $
many places
![]() $\gamma $
with
$\gamma $
with
![]() $f(\gamma )={\langle }{\rangle }$
.
$f(\gamma )={\langle }{\rangle }$
.
As a result, for such
![]() $\gamma $
,
$\gamma $
,
![]() $t_\gamma (0)$
will be determined only after an element of the corresponding set of measure one is picked, and there are
$t_\gamma (0)$
will be determined only after an element of the corresponding set of measure one is picked, and there are
![]() $\kappa $
-many such
$\kappa $
-many such
![]() $\gamma $
’s.
$\gamma $
’s.
However, we do not need the exact value of
![]() $t_\gamma (0)$
, but rather to know whether it is even or odd. This is determined (on a set of measure one) by
$t_\gamma (0)$
, but rather to know whether it is even or odd. This is determined (on a set of measure one) by
![]() $\gamma $
itself. Namely, in this situation,
$\gamma $
itself. Namely, in this situation,
![]() $t_\gamma (0)$
will be even iff
$t_\gamma (0)$
will be even iff
![]() $\gamma $
is even.
$\gamma $
is even.
The rest of the argument is as in Theorem 4.12.
Acknowledgements
The authors would like to thank the referee for their insightful remarks and the improvement of the content of the paper. Also, they would like to thank Mohammad Golshani for his crucial correction in the first draft of the paper. Finally, they would like to thank the participants of the Set Theory Seminar of Tel-Aviv University, and in particular to Menachem Magidor, Carmi Merimovich, and Sittinon Jirattikansakul for their wonderful comments and suggestions.
Funding
The work of the first author was supported by the National Science Foundation under Grant No. DMS-2246703. The work of the second author was partially supported by ISF grants (Nos. 1216/18 and 882/22).