Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-26T06:29:33.577Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CUPPING AND AHMAD PAIRS

Part of: Computability and recursion theory

Published online by Cambridge University Press:  12 December 2022

ISKANDER SH. KALIMULLIN ,
STEFFEN LEMPP Open the ORCID record for STEFFEN LEMPP [Opens in a new window] ,
KENG NG  and
MARS M. YAMALEEV
ISKANDER SH. KALIMULLIN
Affiliation:
N.L. LOBACHEVSKY INSTITUTE OF MATHEMATICS AND MECHANICS KAZAN FEDERAL UNIVERSITY KAZAN 420008, RUSSIA E-mail: [email protected] URL: https://kpfu.ru/Iskander.Kalimullin?p_lang=2 E-mail: [email protected] URL: https://kpfu.ru/Mars.Yamaleev?p_lang=2
STEFFEN LEMPP
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN MADISON, WI 53706-1325, USA E-mail: [email protected] URL: http://www.math.wisc.edu/~lempp/
KENG NG*
Affiliation:
DIVISION OF MATHEMATICAL SCIENCES SCHOOL OF PHYSICAL & MATHEMATICAL SCIENCES COLLEGE OF SCIENCE NANYANG TECHNOLOGICAL UNIVERSITY, SINGAPORE URL: http://www.ntu.edu.sg/home/kmng/
MARS M. YAMALEEV
Affiliation:
N.L. LOBACHEVSKY INSTITUTE OF MATHEMATICS AND MECHANICS KAZAN FEDERAL UNIVERSITY KAZAN 420008, RUSSIA E-mail: [email protected] URL: https://kpfu.ru/Iskander.Kalimullin?p_lang=2 E-mail: [email protected] URL: https://kpfu.ru/Mars.Yamaleev?p_lang=2
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Working toward showing the decidability of the 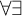$\forall \exists $-theory of the 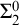${\Sigma ^0_2}$-enumeration degrees, we prove that no so-called Ahmad pair of 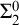${\Sigma ^0_2}$-enumeration degrees can join to 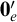${\mathbf 0}_e'$.

Keywords

enumeration degreescuppingAhmad pair

MSC classification

Primary: 03D30: Other degrees and reducibilities
Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 3 , September 2024 , pp. 1358 - 1369
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahmad, S., Some results on the structure of the ${\boldsymbol{\varSigma}}_{\boldsymbol{2}}$ enumeration degrees , Ph.D. thesis, Simon Fraser University, Canada, 1989.Google Scholar
Ahmad, S. and Lachlan, A. H., Some special pairs of ${\varSigma}_2$ e-degrees . Mathematical Logic Quarterly , vol. 44 (1998), no. 4, pp. 431–449.CrossRefGoogle Scholar
Ganchev, H. A. and Soskova, M. I., Interpreting true arithmetic in the local structure of the enumeration degrees, this Journal, vol. 77 (2012), pp. 1184–1194.Google Scholar
Goh, J. L., Ng, K. M., Lempp, S., and Soskova, M. I., Extensions of two constructions of Ahmad. Computability , vol. 11 (2022), no. 3-4, pp. 269–297.Google Scholar
Goh, J. L., Ng, K. M., Lempp, S., and Soskova, M. I., Extensions of embeddings of 1-point extensions of finite antichains in the ${\varSigma}_2^0$ -enumeration degrees, in preparation.Google Scholar
Kent, T. F., The ${\varPi}_3$ -theory of the ${\varSigma}_2^0$ -enumeration degrees is undecidable, this Journal, vol. 71 (2006), pp. 1284–1302.Google Scholar
Lempp, S., Lerman, M., and Reed Solomon, D., Embedding finite lattices into the computably enumerable degrees—A status survey , Logic Colloquium’02 (Z. Chatzidakis, P. Koepke and W. Pohlers, editors), Lecture Notes in Logic, vol. 27, Association for Symbolic Logic, La Jolla, 2006, pp. 206–229.Google Scholar
Lempp, S., Nies, A., and Slaman, T. A., The ${\varPi}_3$ -theory of the computably enumerable Turing degrees is undecidable . Transactions of the American Mathematical Society , vol. 350 (1998), pp. 2719–2736.CrossRefGoogle Scholar
Lempp, S., Slaman, T. A., and Sorbi, A., On extensions of embeddings into the enumeration degrees of the ${\varSigma}_2^0$ -sets . Journal of Mathematical Logic , vol. 5 (2005), pp. 247–298.CrossRefGoogle Scholar
Lempp, S. and Sorbi, A., Embedding finite lattices into the ${\varSigma}_2^0$ -enumeration degrees, this Journal, vol. 67 (2002), pp. 69–90.Google Scholar
Nies, A., Shore, R. A., and Slaman, T. A., Interpretability and definability in the recursively enumerable degrees . Proceedings of the London Mathematical Society (3) , vol. 77 (1998), pp. 241–291.CrossRefGoogle Scholar
Sacks, G. E., On the degrees less than ${\boldsymbol{0}}^{\prime }.$ Annals of Mathematics. Second Series , vol. 77 (1963), pp. 211–231.CrossRefGoogle Scholar
Slaman, T. A. and Woodin, W. H., Definability in the enumeration degrees . Archive for Mathematical Logic , vol. 36 (1997), nos. 4–5, pp. 255–267.CrossRefGoogle Scholar