Let V denote the class of discrete groups G which satisfy the following conditions (a), (b) and (c):

(a) G = (A * B; K = φ(H)) is the free product of two groups A and B with the subgroup H amalgamated.

(b) H does not contain the verbal subgroup A(X2) of A and K does not contain the verbal subgroup B(X2)of B.

This paper is devoted to the determining of the irreducible linear representations of the generalized symmetric group (elsewhere written as , Cm ≀ Sn or G(m, 1, n)) by considering the conjugacy classes of and then constructing the same number of inequivalent irreducible linear representations of . These have previously been determined by Kerber [2, Section 5] using Clifford's theory applied to wreath products.

Throughout we shall consider only finite-dimensional Lie algebras over a field of characteristic zero. In [3] it was shown that the classes of solvable and of supersolvable Lie algebras of dimension greater than two are characterised by the structure of their subalgebra lattices. The same is true of the classes of simple and of semisimple Lie algebras of dimension greater than three. However, it is not true of the class of nilpotent Lie algebras. We seek here the smallest class containing all nilpotent Lie algebras which is so characterised.

We let X be an arbitrary infinite set. A semigroup S of total or partial transformations of X is called -normal if hSh-1 = S, for all h in , the symmetric group on X. For example, the full transformation semigroup , the semigroup of all partial transformations , the semigroup of all 1–1 partial transformations and all ideals of and are -normal.

Dans tout ce qui suit, H désigne un espace de Hilbert séparable, A un opérateur fermé de domaine D(A) dans H, on note B(H) l'ensemble des opérateurs bornés de H dans lui-même et N(A), R(A) respectivement le noyau de A, l'image de A.

En 1958, T. Kato a démontré dans [7] le théorème suivant.

Various authors have obtained an eight term exact sequence in homology

from a short exact sequence of groups

,

the term V varying from author to author (see [7] and [2]; see also [5] for the simpler case where N is central in G, and [6] for the case where N is central and N ⊂ [G, G]). The most satisfying version of the sequence is obtained by Brown and Loday [2] (full details of [2] are in [3]) as a corollary to their van Kampen type theorem for squares of spaces: they give the term V as the kernel of a map G ∧ N → N from a “non-abelian exterior product” of G and N to the group N (the definition of G ∧ N, first published in [2], is recalled below). The two short exact sequences

and

where F is free, together with the fact that H2(F) = 0 and H3(F) = 0, imply isomorphisms

.

.

The isomorphism (2) is essentially the description of H2(G) proved algebraically in [11]. As noted in [2], the isomorphism (3) is the analogue for H3(G) of the Hopf formula for H2(G).

Transitive group representations have their analogue for inverse semigroups as discovered by Schein [7]. The right cosets in the group case find their counterpart in the right ω-cosets and the symmetric inverse semigroup plays the role of the symmetric group. The general theory developed by Schein admits a special case discovered independently by Ponizovskiǐ [4] and Reilly [5]. For a discussion of this topic, see [1, §7.3] and [2, Chapter IV].

It is well known that if α and β are commuting *-automorphisms of a von Neumann algebra M satisfying the equation α + α-1 = β + β-1 then M can be decomposed into a direct sum of subalgebras Mp and M(l − p) by a central projection p in M such that α = β on Mp and α = β-1 on M(1 − p) (see, for instance, [6], [7], [2]). Originally this equation arose in the Tomita-Takesaki theory (see, for example, [11]) in the form of one-parameter modular automorphism groups and later on it has been studied for arbitrary automorphisms and one-parameter groups of automorphisms on von Neumann algebras [7], [8], [9]. In the case of automorphism groups satisfying the above equation, one has a similar decomposition but this time without assuming the commutativity condition (cf. [7], [8]). For another relevant work on one-parameter groups of automorphisms which is close to our papers [7] and [8], we refer to Ciorănescu and Zsidó [1]. Regarding applications, this equation has been used for arbitrary automorphisms in the geometric interpretation of the Tomita-Takesaki theory [2] and in the case of automorphism groups it has been a fundamental tool in the generalization of the Tomita-Takesaki theory to Jordan algebras [3]. We may remark that the decomposition in the commuting case [6], [7] is much simpler than in the case of automorphism groups in the non-commutative situation [8]. In some cases one can obtain the decomposition for an arbitrary pair of automorphisms without assuming their commutativity but the problem in the general case has been unresolved. Recently we have shown that if α and β are *-automorphisms of a von Neumann algebra M satisfying the equation α + α-1 = β + β-1 (without assuming the commutativity of α and β) then there exists a central projection p in M such that α2= β2 on Mp and α2 = β−2 on M(l − p) [10].

For a single space curve (that is, a smooth curve embedded in ℝ3) much geometrical information is contained in the dual and the focal set of the curve. These are both (singular) surfaces in ℝ3, the dual being a model of the set of all tangent planes to the curve, and the focal set being the locus of centres of spheres having at least 3-point contact with the curve. The local structures of the dual and the focal set are (for a generic curve) determined by viewing them as (respectively) the discriminant of a family derived from the height functions on the curve, and the bifurcation set of the family of distance-squared functions on the curve. For details of this see for example [6, pp. 123–8].

Let Mn be the C*-algebra of n × n complex matrices. If A is a C*-algebra, let Mn(A) denote the C*-algebra of n × nmatrices a = [aij] with entries in A. For a linear map between C*-algebras, we define the multiplicity map by A linear map Ø is said to be completely bounded if Let B(A, B), CB(A, B) denote the Banach space of bounded linear maps, the set of completely bounded maps from A to B, respectively.

A tensor is said to be isotropic relative to a group of transformations if its components are invariant under the associated group of coordinate transformations. In this paper we review the classification of tensors which are isotropic under the general linear group, the special linear (unimodular) group and the rotational group. These correspond respectively to isotropic absolute tensors [4, 8] isotropic relative tensors [4] and isotropic Cartesian tensors [3]. New proofs are given for the representation of isotropic tensors in terms of Kronecker deltas and alternating tensors. And, for isotropic Cartesian tensors, we provide a complete classification, clarifying results described in [3].

In the final section of the paper certain derivatives of isotropic tensor fields are examined.

The fundamental work on approximation in weighted spaces of continuous functions on a completely regular space has been done mainly by Nachbin ([5], [6]). Further investigations have been made by Summers [10], Prolla ([7], [8]), and other authors (see the monograph [8] for more references). These authors considered functions with range contained in the scalar field or a locally convex topological vector space. In the present paper we prove some approximation results without local convexity of the range space.

If we seek solutions of the hyperbolic differential equation

which depend only on the variables i and , we see that these solutions must be even in r and satisfy the differential equation

The object of this paper is to show that some recent results in the fractional calculus can be used to prove the following theorem.

In this paper, we continue the work initiated by Morris [5] and Saeed-ul-Islam [6,7] and determine complete sets of inequivalent irreducible projective representations (which we shall write as i.p.r.) of finite Abelian groups with respect to some additional factor sets.

We consider an Abelian group

which will be referred to as an Abelian group of type (a1, …, am).

Let ω be a non-empty set, ℱ a Boolean σ-algebra of subsets of Ω, k a natural number, and let m:ℱ→ℝk be a non-atomic vector measure. Then, by the celebrated theorem of Liapounov [11], the range m[3F] = {m(A): A ε ℱ3F} of m is a compact convex subset of ℝk. This theorem has been generalized in a number of ways. For example Kingman and Robertson [8] and Knowles [9] have shown that, under appropriate conditions, results in the same spirit can be proved for measures taking their values in infinite-dimensional vector spaces. Another type of generalization was obtained by Dvoretsky, Wald and Wolfowitz [6,7]. What they do is to take m as above together with a natural number n≥ 1. They then consider the set Knof all vectors

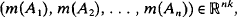
where (A1 A2,…, An) is an ordered ℱ-measurable partition of Ω (i.e. a partition whose terms A, all belong to ℱ). They prove in [6] that Kn is a compact convex subset of ℝnk and moreover that Kn is equal to the set of all vectors of the form

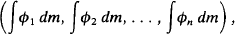
where (ϕ1, ϕ2…, ϕn) is an ℱ-measurable partition of unity; i.e. it is an n-tuple of non-negative ϕr on Ω such that

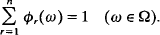
Liapounov's theorem can be obtained as a corollary of this result by taking n= 2.

Throughout this paper S will denote a given monoid, that is, a semigroup with an identity. A set A is a right S-system if there is a map φ: A × S → A satisfying

for any element a of A and any elements s, t of S. For φ(a, s) we write as and we refer to right S-systems simply as S-systems. One has the obvious definitions of an S-subsystem and an S-homomorphism.

Several properties are known to be inherited from the derived factor group of a group G by other factors Γi = γi(G)/γi + 1(G) of the lower central series. Derek Robinson proved [1] that the denning property of any class of groups which is closed under the forming of homomorphic images of tensor products is so inherited. Possibilities for here include the following classes.

The aim of this paper is to prove the irrationality of a certain class of infinite series. The main theorem is related to some results due to Erdos and Straus [7], Erdos [5] and Sándor [15]. As applications of the main result, the solutions of two problems posed by Erdös and Graham [6] are given, among others.

Let Bn denote the unit ball and Un the unit polydisc in Cn. In this paper we consider questions concerned with inner functions and embeddings of Hardy spaces over bounded symmetric domains. The main result (Theorem 2) states that for a classical symmetric domain D of type I and rank(D) = s, there exists an isometric embedding of Hl(Us) onto a complemented subspace of Hl(D). This should be compared with results of Wojtaszczyk [13] and Bourgain [3, 4] which state that H1(Bn) is isomorphic to Hl(U) while for n>m, Hl(Un) cannot be isomorphically embedded onto a complemented subspace of H1(Um). Since balls are the only bounded symmetric domains of rank 1 and they are of type I, Theorem 2 shows that if rank(D1) = 1, rank(D2) > 1 then H1(D1) is not isomorphic to H1(D2). It is natural to expect this to hold always when rank(D1 ≠ rank(D2) but unfortunately we were not able to prove this.

Two numerical characterizations of commutativity for C*-algebra (acting on the Hilbert space H) were given in [1]; one used the norms of self-adjoint operators in (Theorem 2), and the other the numerical index of (Theorem 3). In both cases the proofs were based on the result of Kaplansky which states that if the only nilpotent operator in is 0, then is commutative ([2] 2.12.21, p. 68). Of course the converse also holds.