Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Levi, Inessa
1992.
Injective endomorphisms of $${\cal G}_X - normal$$ semigroups: Infinite defectssemigroups: Infinite defects.
Semigroup Forum,
Vol. 45,
Issue. 1,
p.
9.
Vechtomov, E. M.
1994.
Rings of continuous functions. Algebraic aspects.
Journal of Mathematical Sciences,
Vol. 71,
Issue. 2,
p.
2364.
Дуплий, Степан Анатольевич
Duplij, Steven Anatolievich
Дуплий, Степан Анатольевич
and
Duplij, Steven Anatolievich
1996.
Идеальное строение суперконформных полугрупп.
Теоретическая и математическая физика,
Vol. 106,
Issue. 3,
p.
355.
Levi, Inessa
2001.
Group closures of one-to-one transformations.
Bulletin of the Australian Mathematical Society,
Vol. 64,
Issue. 2,
p.
177.
Araújo, João
and
Konieczny, Janusz
2003.
Automorphism groups of centralizers of idempotents.
Journal of Algebra,
Vol. 269,
Issue. 1,
p.
227.
Pinto, Fernanda A.
and
Sullivan, R.P.
2004.
Baer-Levi semigroups of partial transformations.
Bulletin of the Australian Mathematical Society,
Vol. 69,
Issue. 1,
p.
87.
Araújo, João
and
Konieczny, Janusz
2007.
A method of finding automorphism groups of endomorphism monoids of relational systems.
Discrete Mathematics,
Vol. 307,
Issue. 13,
p.
1609.
ARAÚJO, JOÃO
and
KONIECZNY, JANUSZ
2009.
GENERAL THEOREMS ON AUTOMORPHISMS OF SEMIGROUPS AND THEIR APPLICATIONS.
Journal of the Australian Mathematical Society,
Vol. 87,
Issue. 01,
p.
1.
Araújo, J.
Bünau, P.V.
Mitchell, J.D.
and
Neunhöffer, M.
2010.
Computing automorphisms of semigroups.
Journal of Symbolic Computation,
Vol. 45,
Issue. 3,
p.
373.
Singha, Boorapa
Sanwong, Jintana
and
Sullivan, Robert Patrick
2012.
INJECTIVE PARTIAL TRANSFORMATIONS WITH INFINITE DEFECTS.
Bulletin of the Korean Mathematical Society,
Vol. 49,
Issue. 1,
p.
109.
Araújo, João
Bentz, Wolfram
and
Gomes, Gracinda M. S.
2018.
Congruences on direct products of transformation and matrix monoids.
Semigroup Forum,
Vol. 97,
Issue. 3,
p.
384.
Araújo, João
Bentz, Wolfram
Dobson, Edward
Konieczny, Janusz
and
Morris, Joy
2018.
Automorphism Groups of Circulant Digraphs With Applications to Semigroup Theory.
Combinatorica,
Vol. 38,
Issue. 1,
p.
1.
Al Subaiei, Bana
and
Jarboui, Noômen
2021.
On the Monoid of Unital Endomorphisms of a Boolean Ring.
Axioms,
Vol. 10,
Issue. 4,
p.
305.
Shah, Aftab
Mir, Dilawar
and
Quinn-gregson, Thomas
2024.
Inner automorphisms of Clifford monoids.
Hacettepe Journal of Mathematics and Statistics,
Vol. 53,
Issue. 4,
p.
1060.


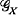 -normal if
-normal if 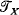 , the semigroup of all partial transformations
, the semigroup of all partial transformations 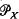 , the semigroup of all 1–1 partial transformations
, the semigroup of all 1–1 partial transformations 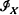 and all ideals of
and all ideals of 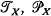 and
and 