Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-04T09:49:07.147Z Has data issue: false hasContentIssue false
  • English
  • Français

On a theorem of Dvoretsky, Wald, and Wolfowitz concerning Liapounov Measures

Published online by Cambridge University Press:  18 May 2009

D. A. Edwards
D. A. Edwards*
Affiliation:
Mathematical Institute, 24–29 St Giles, Oxford OX1 3LB.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ω be a non-empty set, ℱ a Boolean σ-algebra of subsets of Ω, k a natural number, and let m:ℱ→ℝk be a non-atomic vector measure. Then, by the celebrated theorem of Liapounov [11], the range m[3F] = {m(A): A ε ℱ3F} of m is a compact convex subset of ℝk. This theorem has been generalized in a number of ways. For example Kingman and Robertson [8] and Knowles [9] have shown that, under appropriate conditions, results in the same spirit can be proved for measures taking their values in infinite-dimensional vector spaces. Another type of generalization was obtained by Dvoretsky, Wald and Wolfowitz [6,7]. What they do is to take m as above together with a natural number n≥ 1. They then consider the set Knof all vectors

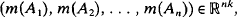
where (A1 A2,…, An) is an ordered ℱ-measurable partition of Ω (i.e. a partition whose terms A, all belong to ℱ). They prove in [6] that Kn is a compact convex subset of ℝnk and moreover that Kn is equal to the set of all vectors of the form

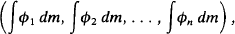
where (ϕ1, ϕ2…, ϕn) is an ℱ-measurable partition of unity; i.e. it is an n-tuple of non-negative ϕr on Ω such that

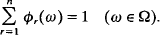
Liapounov's theorem can be obtained as a corollary of this result by taking n= 2.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 29 , Issue 2 , July 1987 , pp. 205 - 220
Copyright
Copyright © Glasgow Mathematical Journal Trust 1987

References

1. Azarnia, N. and Wright, J. D. M., On the Lyapunov–Knowles theorem, Quart. J. Math. Oxford Ser. 2, 33 (1982), 257–261.CrossRefGoogle Scholar
2. Bartle, R. G., Dunford, N. and Schwartz, J. T., Weak compactness and vector measures, Canad. J. Math. 7 (1955), 289–305.CrossRefGoogle Scholar
3. Diestel, J. and Uhl, J. J. Jr, Vector measures, AMS Math. Surveys No. 15 (Providence R.I. 1977).CrossRefGoogle Scholar
4. Dor, L. E., On projections in L1, Ann. of Math. 102 (1975), 463–474.CrossRefGoogle Scholar
5. Dubins, L. E. and Spanier, E. H., How to cut a cake fairly, Amer. Math. Monthly 68 (1961), 1–17.CrossRefGoogle Scholar
6. Dvoretsky, A., Wald, A. and Wolfowitz, J., Relations among certain ranges of vector measures, Pacific J. Math 1 (1951), 51–74.Google Scholar
7. Dvoretsky, A., Wald, A. and Wolfowitz, J., Elimination of randomization in certain statistical decision procedures and zero-sum two-person games, Ann. Math. Statist. 22 (1951), 1–21.CrossRefGoogle Scholar
8. Kingman, J. F. C. and Robertson, A. P., On a theorem of Liapounov, J. London. Math. Soc. 43 (1968), 347–351.CrossRefGoogle Scholar
9. Knowles, G., Liapounov vector measures, SIAM J. Control 13 (1974), 294–303.CrossRefGoogle Scholar
10. Lindenstrauss, J., A short proof of Liapounov's convexity theorem, J. Math. Mech. 15 (1966), 971–972.Google Scholar
11. Lyapunov, A., Sur les fonctions-vecteurs complètement additives, Izv. Akad. Nauk SSSR Ser. Mat. 4 (1940), 465–478.Google Scholar
12. Woodall, D. R., Dividing a cake fairly, J. Math. Anal. Appl. 78 (1980), 233–247.CrossRefGoogle Scholar