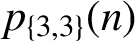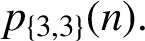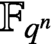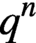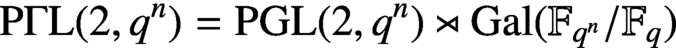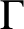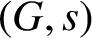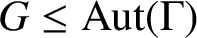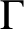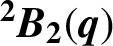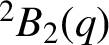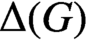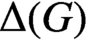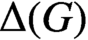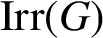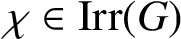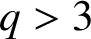Research Article
ON THE SUM OF PARTS IN THE PARTITIONS OF n INTO DISTINCT PARTS
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2020, pp. 228-237
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF 3-REGULAR PARTITIONS IN THREE COLOURS
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2021, pp. 415-423
-
- Article
- Export citation
MÖBIUS–FROBENIUS MAPS ON IRREDUCIBLE POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 14 December 2020, pp. 66-77
-
- Article
- Export citation
DIVISIBILITY OF CERTAIN SINGULAR OVERPARTITIONS BY POWERS OF
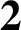 $\textbf{2}$
AND
$\textbf{2}$
AND
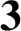 $\textbf{3}$
$\textbf{3}$
- Part of:
-
- Published online by Cambridge University Press:
- 14 January 2021, pp. 238-248
-
- Article
- Export citation
SMOOTH FANO 4-FOLDS IN GORENSTEIN FORMATS
- Part of:
-
- Published online by Cambridge University Press:
- 31 May 2021, pp. 424-433
-
- Article
- Export citation
STRICTLY REAL FUNDAMENTAL THEOREM OF ALGEBRA USING POLYNOMIAL INTERLACING
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2021, pp. 249-255
-
- Article
-
- You have access
- Open access
- Export citation
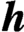 $\textit{h}$
-MINIMUM SPANNING LENGTHS AND AN EXTENSION TO BURNSIDE’S THEOREM ON IRREDUCIBILITY
$\textit{h}$
-MINIMUM SPANNING LENGTHS AND AN EXTENSION TO BURNSIDE’S THEOREM ON IRREDUCIBILITY
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2020, pp. 78-93
-
- Article
- Export citation
FUSION 2-CATEGORIES WITH NO LINE OPERATORS ARE GROUPLIKE
-
- Published online by Cambridge University Press:
- 19 February 2021, pp. 434-442
-
- Article
- Export citation
A NEW ALGORITHM FOR DECOMPOSING MODULAR TENSOR PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2021, pp. 94-107
-
- Article
- Export citation
FIXED POINTS OF POLYNOMIALS OVER DIVISION RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2021, pp. 256-262
-
- Article
- Export citation
STRONGLY BOUNDED LOCALLY INDICABLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2021, pp. 443-447
-
- Article
- Export citation
CLASSIFICATION OF TETRAVALENT
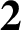 $\textbf{2}$
-TRANSITIVE NONNORMAL CAYLEY GRAPHS OF FINITE SIMPLE GROUPS
$\textbf{2}$
-TRANSITIVE NONNORMAL CAYLEY GRAPHS OF FINITE SIMPLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2021, pp. 263-271
-
- Article
- Export citation
FIXED POINT THEOREM FOR AN INFINITE TOEPLITZ MATRIX
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2020, pp. 108-117
-
- Article
- Export citation
COPRIME COMMUTATORS IN THE SUZUKI GROUPS
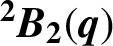 $^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
$^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
- Part of:
-
- Published online by Cambridge University Press:
- 20 January 2021, pp. 448-452
-
- Article
- Export citation
TRIPLET INVARIANCE AND PARALLEL SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 25 January 2021, pp. 118-126
-
- Article
-
- You have access
- Open access
- Export citation
ON ANALOGUES OF HUPPERT’S CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2021, pp. 272-277
-
- Article
- Export citation
THE CHARACTER GRAPH OF A FINITE GROUP IS PERFECT
- Part of:
-
- Published online by Cambridge University Press:
- 18 November 2020, pp. 127-131
-
- Article
- Export citation
AN ANALOGUE OF HUPPERT’S CONJECTURE FOR CHARACTER CODEGREES
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2021, pp. 278-286
-
- Article
- Export citation
CONNECTED COMPONENTS IN THE INVARIABLY GENERATING GRAPH OF A FINITE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2021, pp. 453-463
-
- Article
-
- You have access
- Open access
- Export citation
BEING CAYLEY AUTOMATIC IS CLOSED UNDER TAKING WREATH PRODUCT WITH VIRTUALLY CYCLIC GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 April 2021, pp. 464-474
-
- Article
- Export citation