Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T19:51:28.136Z Has data issue: false hasContentIssue false
  • English
  • Français

MÖBIUS–FROBENIUS MAPS ON IRREDUCIBLE POLYNOMIALS

Part of: General field theory Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  14 December 2020

F. E. BROCHERO MARTÍNEZ Open the ORCID record for F. E. BROCHERO MARTÍNEZ [Opens in a new window] ,
DANIELA OLIVEIRA Open the ORCID record for DANIELA OLIVEIRA [Opens in a new window]  and
LUCAS REIS Open the ORCID record for LUCAS REIS [Opens in a new window]
F. E. BROCHERO MARTÍNEZ
Affiliation:
Departamento de Matemática, Universidade Federal de Minas Gerais, UFMG, Belo HorizonteMG, 31270-901, Brazil e-mail: [email protected]
DANIELA OLIVEIRA
Affiliation:
Departamento de Matemática, Universidade Federal de Minas Gerais, UFMG, Belo HorizonteMG, 31270-901, Brazil e-mail: [email protected]
LUCAS REIS*
Affiliation:
Departamento de Matemática, Universidade Federal de Minas Gerais, UFMG, Belo Horizonte, MG, 31270-901, Brazil
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let n be a positive integer and let 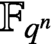$\mathbb{F} _{q^n}$ be the finite field with 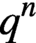$q^n$ elements, where q is a prime power. We introduce a natural action of the projective semilinear group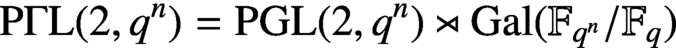 ${\mathrm{P}\Gamma\mathrm{L}} (2, q^n)={\mathrm{PGL}} (2, q^n)\rtimes {\mathrm{Gal}} ({\mathbb F_{q^n}} /\mathbb{F} _q)$ on the set of monic irreducible polynomials over the finite field 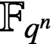$\mathbb{F} _{q^n}$ . Our main results provide information on the characterisation and number of fixed points.

Keywords

enumeration formulafixed pointgroup actionirreducible polynomials over finite fields

MSC classification

Primary: 11T06: Polynomials
Secondary: 12E20: Finite fields (field-theoretic aspects)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 66 - 77
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was partially supported by FAPEMIG APQ-02973-17, Brazil. The third author was supported by FAPESP 2018/03038-2, Brazil.

References

Boripan, A., Jitman, S. and Udomkavanich, P., ‘Self-conjugate-reciprocal irreducible monic polynomials over finite fields’, Proc. 20th Annu. Meet. Mathematics 2015 (Silpakorn University, Nakhon Pathom, Thailand, 2015), 34–43.Google Scholar
Boripan, A., Jitman, S. and Udomkavanich, P., ‘Self-conjugate-reciprocal irreducible monic factors of ${x}^n-1$ over finite fields and their applications’, Finite Fields Appl. 55 (2019), 78–96.CrossRefGoogle Scholar
Garefalakis, T., ‘On the action of $\mathrm{GL}(2,q)$ on irreducible polynomials over ${F}_q$ ’, J. Pure Appl. Algebra 215 (2011), 1835–1843.CrossRefGoogle Scholar
Mattarei, S. and Pizzato, M., ‘Generalizations of self-reciprocal polynomials’ Finite Fields Appl. 48 (2017), 271–288.CrossRefGoogle Scholar
Meyn, H. and Götz, W., ‘Self-reciprocal polynomials over finite fields’, Publ. Inst. Rech. Math. Av. 413(21) (1990), 82–90.Google Scholar
Reis, L., ‘The action of ${\mathrm{GL}}_2({F}_q)$ on irreducible polynomials over ${F}_q$ , revisited’, J. Pure Appl. Algebra 222 (2018), 1087–1094.CrossRefGoogle Scholar
Stichtenoth, H. and Topuzoğlu, A., ‘Factorization of a class of polynomials over finite fields’, Finite Fields Appl. 18 (2012), 108–122.CrossRefGoogle Scholar