Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Johnson-Freyd, Theo
and
Yu, Matthew
2022.
Topological Orders in (4+1)-Dimensions.
SciPost Physics,
Vol. 13,
Issue. 3,
Antinucci, Andrea
Galati, Giovanni
and
Rizi, Giovanni
2022.
On continuous 2-category symmetries and Yang-Mills theory.
Journal of High Energy Physics,
Vol. 2022,
Issue. 12,
Bhardwaj, Lakshya
Schäfer‐Nameki, Sakura
and
Wu, Jingxiang
2022.
Universal Non‐Invertible Symmetries.
Fortschritte der Physik,
Vol. 70,
Issue. 11,
Décoppet, Thibault D.
and
Yu, Matthew
2023.
Gauging noninvertible defects: a 2-categorical perspective.
Letters in Mathematical Physics,
Vol. 113,
Issue. 2,
Choi, Yichul
Córdova, Clay
Hsin, Po-Shen
Lam, Ho Tat
and
Shao, Shu-Heng
2023.
Non-invertible Condensation, Duality, and Triality Defects in 3+1 Dimensions.
Communications in Mathematical Physics,
Vol. 402,
Issue. 1,
p.
489.
Johnson-Freyd, Theo
and
Reutter, David
2023.
Minimal nondegenerate extensions.
Journal of the American Mathematical Society,
Vol. 37,
Issue. 1,
p.
81.
Heckman, Jonathan J.
McNamara, Jacob
Montero, Miguel
Sharon, Adar
Vafa, Cumrun
and
Valenzuela, Irene
2024.
Fate of stringy noninvertible symmetries.
Physical Review D,
Vol. 110,
Issue. 10,
Schäfer-Nameki, Sakura
2024.
ICTP lectures on (non-)invertible generalized symmetries.
Physics Reports,
Vol. 1063,
Issue. ,
p.
1.
Buican, Matthew
and
Radhakrishnan, Rajath
2024.
Invertibility of Condensation Defects and Symmetries of 2 + 1d QFTs.
Communications in Mathematical Physics,
Vol. 405,
Issue. 9,
Bartsch, Thomas
Bullimore, Mathew
Ferrari, Andrea E. V.
and
Pearson, Jamie
2024.
Non-invertible symmetries and higher representation theory I.
SciPost Physics,
Vol. 17,
Issue. 1,
Córdova, Clay
Hsin, Po-Shen
and
Zhang, Carolyn
2024.
Anomalies of non-invertible symmetries in (3+1)d.
SciPost Physics,
Vol. 17,
Issue. 5,
Kong, Liang
and
Zheng, Hao
2024.
Categories of Quantum Liquids II.
Communications in Mathematical Physics,
Vol. 405,
Issue. 9,
Décoppet, Thibault D.
and
Yu, Matthew
2025.
Fiber 2-Functors and Tambara–Yamagami Fusion 2-Categories.
Communications in Mathematical Physics,
Vol. 406,
Issue. 3,
Johnson-Freyd, Theo
2025.
Quantum Symmetries.
Vol. 813,
Issue. ,
p.
175.
Décoppet, Thibault D.
2025.
Finite semisimple module 2-categories.
Selecta Mathematica,
Vol. 31,
Issue. 1,
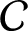 ${\mathcal C}$
is a fusion
${\mathcal C}$
is a fusion
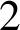 $2$
-category in which the endomorphism category of the unit object is
$2$
-category in which the endomorphism category of the unit object is
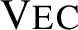 or
or
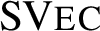 , then the indecomposable objects of
, then the indecomposable objects of
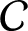 ${\mathcal C}$
form a finite group.
${\mathcal C}$
form a finite group.