Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T20:23:20.917Z Has data issue: false hasContentIssue false
  • English
  • Français

TRIPLET INVARIANCE AND PARALLEL SUMS

Part of: Homological methods Radicals and radical properties of rings

Published online by Cambridge University Press:  25 January 2021

TSIU-KWEN LEE Open the ORCID record for TSIU-KWEN LEE [Opens in a new window] ,
JHENG-HUEI LIN Open the ORCID record for JHENG-HUEI LIN [Opens in a new window]  and
TRUONG CONG QUYNH Open the ORCID record for TRUONG CONG QUYNH [Opens in a new window]
TSIU-KWEN LEE*
Affiliation:
Department of Mathematics, National Taiwan University, Taipei106, Taiwan
JHENG-HUEI LIN
Affiliation:
Department of Mathematics, National Taiwan University, Taipei106, Taiwan e-mail: [email protected]
TRUONG CONG QUYNH
Affiliation:
Department of Mathematics, The University of Da Nang–University of Science and Education, Da Nang City, Vietnam e-mail: [email protected]
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a semiprime ring with extended centroid C and let 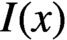$I(x)$ denote the set of all inner inverses of a regular element x in R. Given two regular elements 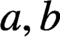$a, b$ in R, we characterise the existence of some 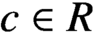$c\in R$ such that 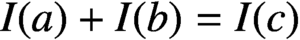$I(a)+I(b)=I(c)$ . Precisely, if 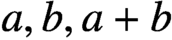$a, b, a+b$ are regular elements of R and a and b are parallel summable with the parallel sum 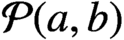${\cal P}(a, b)$ , then 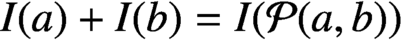$I(a)+I(b)=I({\cal P}(a, b))$ . Conversely, if 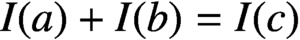$I(a)+I(b)=I(c)$ for some 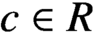$c\in R$ , then 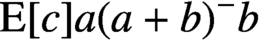$\mathrm {E}[c]a(a+b)^{-}b$ is invariant for all 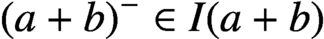$(a+b)^{-}\in I(a+b)$ , where 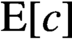$\mathrm {E}[c]$ is the smallest idempotent in C satisfying 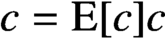$c=\mathrm {E}[c]c$ . This extends earlier work of Mitra and Odell for matrix rings over a field and Hartwig for prime regular rings with unity and some recent results proved by Alahmadi et al. [‘Invariance and parallel sums’, Bull. Math. Sci.10(1) (2020), 2050001, 8 pages] concerning the parallel summability of unital prime rings and abelian regular rings.

Keywords

abelian ringextended centroidinner inverseparallel summableregular elementsemiprime (prime) ringtriplet invariance

MSC classification

Primary: 16N60: Prime and semiprime rings
Secondary: 16E50: von Neumann regular rings and generalizations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 118 - 126
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Australian Mathematical Publishing Association Inc. 2021

Footnotes

The work of T.-K. Lee and J.-H. Lin was supported in part by the Ministry of Science and Technology of Taiwan (MOST 109-2115-M-002-014). The work of T. C. Quynh was supported in part by the Ministry of Education and Training of Vietnam (B2020-DNA-10).

References

Alahmadi, A., Jain, S. K. and Leroy, A., ‘Regular elements determined by generalized inverses’, J. Algebra Appl. 18(7) (2019), 1950128, 6 pages.CrossRefGoogle Scholar
Alahmadi, A., Jain, S. K. and Leroy, A., ‘Invariance and parallel sums’, Bull. Math. Sci. 10(1) (2020), 2050001, 8 pages.CrossRefGoogle Scholar
Anderson, W. N. and Duffin, R. J., ‘Series and parallel addition of matrices’, J. Math. Anal. Appl. 26 (1969), 576–594.CrossRefGoogle Scholar
Beidar, K. I., Martindale, W. S. III and Mikhalev, A. V., Rings with Generalized Identities, Monographs and Textbooks in Pure and Applied Mathematics, 196 (Marcel Dekker, New York, 1996).Google Scholar
Goodearl, K. R., Von Neumann Regular Rings, 2nd edn (Krieger, Malabar, FL, 1991).Google Scholar
Han, J., Lee, Y. and Park, S., ‘Structure of abelian rings’, Front. Math. China 12(1) (2017), 117–134.CrossRefGoogle Scholar
Hartwig, R. E., ‘A remark on the characterization of the parallel sum of two matrices’, Linear Multilinear Algebra 22(2) (1987), 193–197.CrossRefGoogle Scholar
Lee, T.-K., ‘A note on inner and reflexive inverses in semiprime rings’, J. Algebra Appl. 19(10) (2020), 2050197, 4 pages.CrossRefGoogle Scholar
Lee, T.-K. and Lin, J.-H., ‘Outer inverses, minus partial orders and triplet invariance’, Publ. Math. Debrecen 98 (2021), to appear.CrossRefGoogle Scholar
Mitra, S. K., Bhimasankaram, P. and Malik, S. B., Matrix Partial Orders, Shorted Operators and Applications, Series in Algebra, 10 (World Scientific, Hackensack, NJ, 2010).CrossRefGoogle Scholar
Mitra, S. K. and Odell, P. L., ‘On parallel summability of matrices’, Linear Algebra Appl. 74 (1986), 239–255.CrossRefGoogle Scholar
Rao, C. R. and Mitra, S. K., Generalized Inverse of Matrices and its Applications (Wiley, New York, 1971).Google Scholar