Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T10:00:22.114Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CHARACTER GRAPH OF A FINITE GROUP IS PERFECT

Part of: Representation theory of groups Graph theory

Published online by Cambridge University Press:  18 November 2020

MAHDI EBRAHIMI Open the ORCID record for MAHDI EBRAHIMI [Opens in a new window]
MAHDI EBRAHIMI*
Affiliation:
School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box 19395-5746, Tehran, Iran
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a finite group G, let 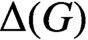$\Delta (G)$ denote the character graph built on the set of degrees of the irreducible complex characters of G. A perfect graph is a graph $\Gamma $ in which the chromatic number of every induced subgraph 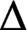$\Delta $ of $\Gamma $ equals the clique number of 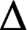$\Delta $ . We show that the character graph 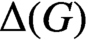$\Delta (G)$ of a finite group G is always a perfect graph. We also prove that the chromatic number of the complement of 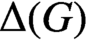$\Delta (G)$ is at most three.

Keywords

character degreecharacter graphperfect graph

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 05C17: Perfect graphs 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 127 - 131
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported in part by a grant from the School of Mathematics, Institute for Research in Fundamental Sciences (IPM).

References

Akhlaghi, Z., Casolo, C., Dolfi, S., Khedri, K. and Pacifici, E., ‘On the character degree graph of solvable groups’, Proc. Amer. Math. Soc. 146 (2018), 1505–1513.CrossRefGoogle Scholar
Akhlaghi, Z., Casolo, C., Dolfi, S., Pacifici, E. and Sanus, L., ‘On the character degree graph of finite groups’, Ann. Mat. Pura Appl. 198 (2019), 1595–1614.CrossRefGoogle Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory, Graduate Texts in Mathematics, 244 (Springer, New York, 2008).CrossRefGoogle Scholar
Chudnovsky, M., Robertson, N., Seymour, P. and Thomas, R., ‘The strong perfect graph theorem’, Ann. Math. 164(1) (2006), 51–229.CrossRefGoogle Scholar
Hosseinzadeh, S., Iranmanesh, A., Hosseinzadeh, M. A. and Lewis, M. L., ‘On graphs associated with character degrees and conjugacy class sizes of direct product of finite groups’, Canad. Math. Bull. 58 (2015), 105–109.CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, San Diego, CA, 1976).Google Scholar
Lewis, M. L., ‘An overview of graphs associated with character degrees and conjugacy class sizes in finite groups’, Rocky Mountain J. Math. 38(1) (2008), 175–211.CrossRefGoogle Scholar
Lovasz, L., ‘A characterization of perfect graphs’, J. Combin. Theory Ser. B 13 (1972), 95–98.CrossRefGoogle Scholar
Manz, O., Staszewski, R. and Willems, W., ‘On the number of components of a graph related to character degrees’, Proc. Amer. Math. Soc. 103 (1) (1988), 31–37.CrossRefGoogle Scholar
Manz, O. and Wolf, T. R., Representations of Solvable Groups, London Mathematical Society Lecture Note Series, 185 (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Moreto, A. and Tiep, P. H., ‘Prime divisors of character degrees’, J. Group Theory 11(3) (2008), 341–356.CrossRefGoogle Scholar
Palfy, P., ‘On the character degree graph of solvable groups. I. Three primes’, Period. Math. Hungar. 36(1) (1998), 61–65.CrossRefGoogle Scholar
Thompson, J. G., ‘Normal $p$ -complements and irreducible characters’, J. Algebra 14 (1970), 129–134.CrossRefGoogle Scholar
White, D. L., ‘Degree graphs of simple linear and unitary groups’, Comm. Algebra 34(8) (2006), 2907–2921.CrossRefGoogle Scholar